Pilot study of isothermal crystallization of goethite from metastable synthetic pyrrhotite

Nowadays the interest to the minerals containing the hydroxyl group (OH) in their structure has increased significantly. Goethite FeO(HO ), hydronium Fe (SO 4 ) 2 (OH) 5 2H 2 O , parabutlerite Fe (SO₄) (OH) 2H₂O etc. can serve as examples of such minerals. This interest can be explained by the fact that their formation is supposed to be connected with hydrothermal metasomatic processes. Such processes are widely developed in volcanic zones on dry land and in oceans. Studying of natural minerals in such zones is actual from the point of view of theoretical and practical geology. It should be noted that the oxidation processes of multi-component alloys have their own features [1]. Ocean pools contain large volumes of valuable mineral resources. In particular, iron-manganese concretions and sulphide accumulations with gold and platinoid admixtures in the formations of black smokers are of practical interest. Necessity of detailed study of formation processes for such minerals is obvious, however, they should be divided in, at least, two sections. The first section is studying minerals of ore masses directly in the process of primary ores formation, which, as a rule, are in a metastable phase. The second section of the research is studying the transformation of minerals during ores oxidation, and transition of metastable minerals into the stable phase. One of the minerals being formed in

* Corresponding author E-mail address: VOnufriynok@.sfu-kras.ru endogenic ores of igneous and hydrothermal deposits is pyrrhotite. It usually possesses varying non-stoichiometric composition, and its crystal structure contains cationic vacancies [2-4]. Distribution of dot defects in the structure depends on free energy of the crystal. Therefore, transition into the stable condition is diffusible and depends on time [5-7]. The processes of minerals transition (pyrrhotite in particular) into the stable phase have not been investigated well enough yet. Experimental study of minerals formation is complicated by the fact that usually it is a very long process in time. Theoretical assumptions when applied can appear to be not absolutely correct. Therefore, long-term experiments, during which transformations of minerals in isothermal conditions in the atmosphere of the Earth were observed, represent indisputable interest.

Purpose of Work

We decided to try and experimentally study the metasomatic transformations of minerals as a result of their ageing (29 years) in the atmosphere of the Earth on the example of metastable pyrrhotites of different chemical and phase composition. At that we also tried to track possible pyrrhotite transformation in a water- containing atmosphere into new minerals, the structure of which contains water or group (OH) . In the final part of the mineralogical experiment we tried to give the theoretical explanation of revealed regularities in formation of balanced phase ratios in synthetic iron sulphide samples at their isothermal ageing in the atmosphere of the Earth.

Samples

Samples with various sulphur and iron ratios S/Fe ( _х ) were prepared using the method of dry synthesis in vacuum at temperature 1000 °C. The estimated ratio varied within the range of 1.0 < х < 2.0 . The samples were synthesized in 1979 [6] in the laboratory of the L.V. Kirenskogo Institute for Physics (Krasnoyarsk, Russia).

The received samples were analysed on the DRON-3 diffractometer using X-ray radiation Со (К_α) . The speed of diffractograms shooting equaled 1°/min in a continuous mode and 0.001 °⁄с in a discrete mode. The filter of β – radiation from iron was used during diffractograms shooting.

The X-ray analysis of the samples showed that there are no compounds containing oxygen, hydrogen or hydroxyl group (OH) in their crystal structure. The samples contained only pyrite FeS₂ and pyrrhotite FeS x of various compositions, defending on the sulphur and iron ratio. The results of study of the phase composition and the crystal structure of phases of produced samples were published in 1982 [8]. Samples of sulphides of complex phase composition, varying in the qualitative and quantitative ratio of their associations, were produced depending on quantitative iron and sulphur ratios in the initial blend.

With the prevailing amount of iron (up to 50 % of Fe atoms) in the initial blend, the ferromagnetic form – αFe and the antiferromagnetic phase of iron sulphide were received. In the narrow range of compositions containing ~50 % of Fe atoms, there is only one antiferromagnetic phase – troilite ( Phase β 2 ). It has a hexagonal cell with the following parameters: а=5.95 Å and с =11.75Å . In the range of 50 % to 48.08 % of Fe atoms there are two antiferromagnetic phases – β₁ and β₂ , differing in parameters of the unit cell. Phase β 1 has the structure of hexagonal low-temperature pyrrhotite with the following unit cell parameters: а=3.44 Å and с =5.78Å . The percent ratio of β₂ and β₁ phases in samples varies depending on iron concentration in the initial blend. In the system containing

48.08 to 47.51 % of Fe atoms, a homogeneous solid solution Fe-S-□ (vacancy) is formed. With the increase of sulphur content Phase β 1 is not formed, and only Phase β 2 exists in the range of 48.08 to 47.6 % Fe atoms. At that the unit cell parameters of this phase vary smoothly from а=3.44 Å and с=5.76 Å to а=3.44 Å and с=5.72 Å depending on the percent content of Fe in the initial blend. With further increase of the sulphur content in the Fe-S system, ferromagnetic phase β₃ is formed, in which the level of vacancy regulation in subbarrays depends on the composition, as nuclear gamma resonance spectra showed. Phase β₃ is formed with Fe atoms concentration in the blend from 47.6 to 47.3 %.

Phase β₄ with a monoclinic structure and high intensity of magnetization ( I_s=19 Gs ∙cm³ /g ) is crystallized together with Phase β 3 in the zone of Fe atoms concentration from 47.3 to 45.9 %, whereas Phases β₁ , β_{2 ,} β₃ have a hexagonal structure.

With Fe atoms concentration in the blend below 45.9 %, the paramagnetic γ -phase with a facecentered cubic lattice was crystallized. Two phases β₄ and γ exist approximately till 34 % of Fe atoms with gradual change of the relative content of these phases depending on the composition. Pure sulphur exists simultaneously with γ –phase with further increase of the sulphur content.

After synthesis the samples were maintained during 29 years at the room temperature (~ 20°С) in atmospheric conditions. In 2008 X-ray structural study of the phase composition was carried out in these samples in the laboratory of the Siberian Federal University (Krasnoyarsk, Russia).

Experiment Results

As a result of the analysis of the obtained X-ray difractograms it has been established that all the samples contained compounds with the hydroxyl group (ОН) in the structure. These included parabutlerite Fe(SO₄)(OH)₂H₂O , goethite FeO(HO) , czomolnokite Fe(SO₄)(H₂O) , hydronium Fe(SO 4 ) 2 (OH) 5 2H 2 O , rozenite Fe(SO 4 )4(H 2 O) and rhomboclase FeH(SO 4 ) 2 4(H 2 O) . As was defined earlier, synthesized samples initially contained pyrrhotite in a metastable phase only. At that it was found out that the series of stable pyrrhotites did not contain phases with the hydroxyl group. These are mineral phases of the following compositions: FeS, Fe₉S_11, Fe₇S₈, Fe₁₉S₂₀, Fe₁₀S₁₁ . The results of the research allow to assume that metastable pyrrhotites in isothermal conditions of modern atmosphere form compounds, the structure of which contains the hydroxyl group, and they do not transform into stable phases of pyrrhotites with time. No compounds, in the structure of which oxygen was present without hydrogen, were observed. For example, FeО, Fe (SО₄)₂, Fe₂О₃ or Fe 3 О 4 .

As a result of the analysis of X-ray patterns it has been found out that for the last 29-year interval of time pure iron has undergone no oxidation. In X-ray patterns where there was pure iron unreacted during the experiment, no magnetite or other oxides of iron were found.

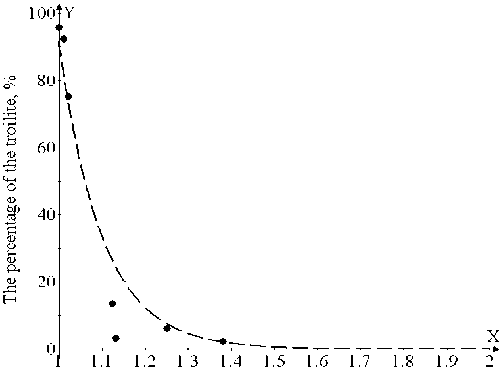
Earlier it was found out that the content of troilite with sulphides synthesis was increasing with the increase of iron in the samples. The dependence of the percent troilite content on the sulphur and iron ratio (S/Fe) in samples is given in Fig. 1. This dependence can be presented in the following way: y=(1.96∙106)∙exp(-10.06∙x) , where y corresponds to the percent troilite content in samples.

The phase composition of samples containing troilite is given in Table 1. It should be noted that sulphur in a free state was excluded for calculation of phase percentage.

S/Fe ratio in samples

Fig. 1. Dependence of troilite percentage on the sulphur and iron ( S/Fe ) rat io in samples

S/Fe ratio in samples

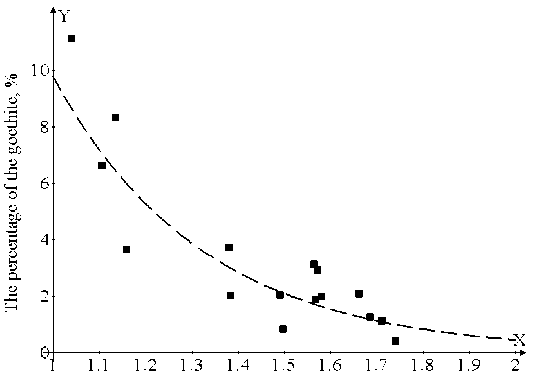
Fig. 2. Dependence of goethite percentage on S/Fe ratio in samples

From the analysis of spectra we can assume that metastable pyrrhotites in conditions of impact of the atmospheric water pass in due course into goethite. Possibly, pyrrhotite of intermediate composition (for example, Fe_0,98S ) disintegrates into goethite and pyrrhotite with composition Fe_0,95S .

Near stoichiometric FeS ( S/Fe = 1.04) the content of goethite was maximal, and made 10.88 %. At the increase of S/Fe ratio the goethite content exponentially fell down. For example, for х = 1.105 it made already 6.62 %. The dependence of goethite percentage on S/Fe ratio in samples is given in Fig. 2. This dependence is described by the formula: y=216.1∙exp(-3.1∙x), where y corresponds to goethite percentage in the samples.

The phase composition of samples containing goethite is given in Table 2.

Table 1 Phase composition of aged samples containing troilite

Mineral Phases	Sample No
	1	2	3	4	5	6	7
S/Fe ratio in samples	1.00	1.010	1.022	1.124	1.125	1.131	1.380
Troilite (β 2 ) – FeS %	95.80	92.38	75.25	13.41	6.11	3.28	2.36
Pyrrhotite (β 4 ) – Fe 7 S 8 %	1.14	7.62	11.82	86.52	70.11	96.34	30.38
Pyrrhotite (β 1 ) – Fe 0.975 S, %	2.75	-	12.93	-	-	-	-
Pyrite (γ) – FeS 2 , %	-	-	-	-	18.52	-	41.14
Czomolnokite – Fe(SO 4 )(H 2 O), %	-	-	-	-	5.07	-	21.04
Goethite – FeO(OH), %	-	-	-	-	-	-	3.73

Table 2 Phase composition of aged samples containing goethite

Mineral Phases	Sample No
	1	2	3	4	5	6	7
S/Fe ratios in samples	1.039	1.105	1.134	1.158	1.380	1.571	1.741
Pyrrhotite (β 4 ) – Fe 7 S 8 , %	69.20	81.79	70.19	73.18	30.38	16.30	3.73
Pyrite (γ) -FeS 2 , %	7.15	5.05	11.87	7.98	41.14	58.49	67.02
Czomolnokite – Fe(SO 4 )(H 2 O), %	12.52	-	-	6.19	21.04	17.36	28.84
Goethite – FeO(OH), %	11.13	6.62	8.34	3.65	3.73	2.93	0.40

The following question occurs: as the result of what does goethite disappear and troilite occur in the samples under study? The authors think that troilite does not disappear and does not occur but is present in samples from the moment of their synthesis in an unchanged state. This phase is stable. Troilite is an extremely stable phase and does not decompose into iron and sulphur, even in the gaseous state. Tests on troilite sputtering to the glass surface were carried out. The difractogram of the received sample given in Fig. 3 testifies to the troilite composition of sputtered material as such.

Goethite percentage, according to the authors, depends on the content of metastable pyrrhotite in initial samples. Metastable pyrrhotite as such under the impact of atmospheric water transforms to goethite in time. There was maximum amount of pyrrhotite in the samples after synthesis with the S/ Fe ratio similar to troilite. The higher the sulphur to iron ratio, the higher percentage in initial samples of iron sulphides in the stable phase state and, correspondingly, the least percentage of goethite in samples after ageing in conditions of the impact of atmospheric air. This explains reduction of the phase composition of goethite with the increase of the S/Fe ratio in the diagram (see Fig. 2).

The analysis of the phase structure and the description of other compounds (czomolnokite, hydronium, rozenite, rhomboclase) containing (OH) in the structure, are beyond the topic of this work.

Mathematical Model of Phase Transformation

To explain the obtained experimental results the mathematical model of phase transformations is offered.

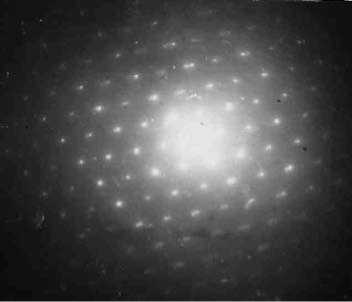
Fig. 3 Reciprocal lattice rec eived with the method of electronic diffraction of troilite sputtered to the glass surface

Let us consider the unit cells in the crystal as some system of N identical cells. The distribution of cells by different volumes can vary; therefore the statistics of cells should be Bose. In order to describe the cells’ power states it is necessary to enter operators of birth and destruction of a cell in some individual volu

\а а'I Л " а2 = (й+ Т=0'ии =п ap , aq pq ; p p       ; ap ap np where p is the number of individual volume of the crystal lattice.

Fourier image of the Green’s function a а Р к + )е

+о

J G pq (t > Et dt - o where

Gp, (t)-«(,)ap(tJa+(0))

is the Green’s function, and

9 ( t) =

1, t

0, t

> 0 1

< ⁰ J ’

t is the variable of time

Hamiltonian describing power states can be written down in the form of:

H = y^a„- a„ + yv„nfia p p p         pq p q p                p,q where the first sum describes independent cells, and the second one – their interaction.

If in some volume of the crystal the unit cell of a new phase was formed, then the energy of the crystal will change with the ε p value.

Taking into consideration commutative relations of the operators after application of the spectral theorem, we get the expression for the average value of the operator of the particles number:

/ ₊ \      1

\a p a p/ = П

I f B ( E И a p| a +) E +. dE = f в I ^ p + Z V p, ^ ,)

—„                                 V q where fB stands for the Bose-Einstein function

Let us introduce the following designations:

n а. = n P p ) n в = n q q)

This is the average number of cells of pyrrhotite corresponding to the composition FeS _x and goethite ( α and β correspondingly), falling to some individual volume of the crystal structure (i.e. n α and n β are proportional to the concentration).

We receive the following system of equations:

” . - f в ( ” + V , )

« , ^- f . ⁽= ^{+ Y} V” a ) , .

where ε α = ε β = ε, and γ is the coordination number for unit cells.

In case of long-term ageing of samples the influence of temperature can be almost excluded, and all processes in crystal structures can be considered as caused mainly by various exchange interactions. This assumption in mathematical respect corresponds to the area of low temperatures e + yVn a, e >> kT

Hence, we can write down:

П а = exp( -      );

n e = ^exp( - ^1+Y S ¹- )■

The obtained exponential dependence of goethite concentration on the S/Fe ratio (that is conditionally equivalent to pyrrhotite of FeS x structure) is in qualitative conformity with the experimental results. The similar model can be applied to troilite at its formation.

Calculations on the basis of the offered quantum model of phases formation show that if the unit cell of goethite was formed in some volume of the crystal, the energy of the crystal will change for 0.13 eV value and if the cell of troilite structure was formed, the energy should change for 17.5∙10³ eV value. The numerical values have been received as a result of comparison of the experimental dependences presented above with theoretically received final formulas. From the calculations done it follows that goethite can be easily formed from pyrrhotite while this process requires essentially less energy than for troilite formation. Thus, troilite can be formed during synthesis only, and formation of troilite from pyrrhotite is almost impossible in due course. Interaction of pyrrhotite – goethite and pyrrhotite – troilite cells from the presented model equal to 10^-2 eV and 0.3 eV correspondingly. This can be explained by the fact that crystal structures of troilite and pyrrhotite in many respects are identical. The crystal structure of goethite differs more sufficiently from the structure of pyrrhotite. That fact that interaction of cells of related structures in the pyrrhotite – troilite system significantly exceeds interaction in the goethite – pyrrhotite system does not cause any questions. In fact, power connection of cells of related structures should be more significant than connection of structurally different cells.

Interaction of cells in the crystal structure is defined, first of all, by the integrals of exchange interaction. The values of these integrals are calculated in the work within the frames of the – 129 – molecular field model, i.e. with another method of quantum mechanics. For pyrrhotite the crystal structure of which in many respects is similar to the structure of pyrrhotite, they equal to 3.4 ∙10-2 eV and 4.25∙10-2 eV, which corresponds to the values of exchange integrals inside the basic planes and between them (i.e. along crystallographic axes “a” and “c” accordingly). The value of interaction of basic troilite unit cells – 30∙10-2 eV received in this work is in good conformity with the results of quantum calculations using the method of a molecular field for pyrrhotite [2]. In fact, for calculations done in this work the coordination number for the structure of pyrrhotite can be accepted as 8 (i.e. the contribution of superexchange interaction was taken into account as well). Let us remind that pyrrhotite possesses the crystal structure of NiAs type [3]. If the averaged value of the exchange integral is multiplied by 8, we will receive the value of energy interaction of cells calculated in this work using the method of secondary quantization (i.e. ≈ 30∙10-2 eV). Thus, the calculations of the similar parameters in various works done using various methods are in good conformity with each other.

One can give the following explanation to the phase transformation described above: hydrogen of a polar water molecule is grasped by the cation vacancy of metastable pyrrhotite and diffuses into the crystal structure, capturing oxygen as well, where new connections are formed transforming pyrrhotite into goethite.

Conclusions

Inhomogeneity of the composition of sulphide phases with a various level of stoichiometry and stability in synthesized samples and the dependence of troilite percentage (stable phase) on the sulphur and iron ratio in the initial blend have been defined.

The dependence of goethite percentage on the sulphur and iron ratio in samples has been determined. It was defined experimentally that goethite was formed as a result of isothermal transformation of metastable pyrrhotite to goethite in atmospheric conditions, with the diffusion mechanism of exchange reactions. Usually, the extremely slow diffusion process of metasomatic reactions (intra-crystal diffusion is limited by first centimeters per million years) is assisted by almost instantaneous (from the point of view of geological time perception) pyrrhotite replacement with goethite.

The quantum-mechanical model of pyrrhotite transition to goethite has been offered. Within the frames of the offered model the calculations of power parameters of pyrrhotite – goethite and pyrrhotite – troilite systems were done. The theoretical substantiation of transformation of metastable pyrrhotite into goethite is given. The calculations carried out in the offered secondary quantization model cohere well with the similar calculations done within the frames of the molecular field model in the other work [1].