Pipelined Vedic-Array Multiplier Architecture

Published Online May 2014 in MECS DOI: 10.5815/ijigsp.2014.06.08

Multiplier is one of the key hardware blocks in designing arithmetic, signal and image processors. Many transform algorithms like the basic building blocks in Fast Fourier transforms, DCT, DFT etc., make use of multipliers. High performance multipliers [1] using Vedic mathematics [2] are proposed and conclude that it is suitable for high-speed complex arithmetic circuits [3]. The basic idea behind all these attempts was the fast implementation of the multiplier and addition [4] of the partial products [5]. Innumerable schemes have been proposed for realization of this operation [6]. With advances in technology, many researchers have tried to design multipliers using Vedic sutras [7], which offer high speed [8], low power consumption [9], and regularity of layout and less area or even combination of them in multiplier [10].

Multiplier is time-consuming operations in many of the digital signal processing applications [11] and computation can be reduced using the Vedic sutras and the overall processor [12] performance can be improved for many applications. Therefore, the goal is to create hybrid architectures that is comparable in speed, area and power, but requires less area than a design using a standard multiplier. The motivation behind this work is to explore the Design and implementation of hybrid multiplier architecture. The proposed pipelined Vedic-Array multiplier is based on the Vedic Sutras.

This paper is organized as follows. Section II gives the overview of Vedic mathematics, Section III briefs about proposed architecture section IV discusses about synthesis and simulation results analysis and section V about conclusion.

• II.    Vedic mathematics

  Vedic Mathematics (VM) is an ancient system of mathematics that was re-discovered by Sri Bharati Krishna Tirthaji between 1911 and 1918. Tirthaji (18841960) was an Indian scholar well versed in the areas of Sanskrit, English, Mathematics, Astronomy and many other areas of science. He deciphered ancient Indian texts, known as the “Ganita Sutras”, (which means mathematics) to discover 16 short verses, known as “Sutras”. These sutras, when applied correctly, will enable the user to solve many types of math problems mentally without having to use pencil and paper in a fraction of the time in would take otherwise. Tirthaji wrote sixteen books, one for each sutra, describing the application of each to the solution of math problems. Unfortunately, these books were lost. Tirthaji attempted to re-write all of these books from memory, but, was only able to complete the first volume entitled “Vedic Mathematics” before his death. This book, which is available today, is the seminal work on Vedic Mathematics.

Swami Bharati Krishna Tirtha (1884-1960), former Jagadguru Sankaracharya of Puri culled a set of 16 Sutras (aphorisms) and 13 Sub - Sutras (corollaries) from the Atharva Veda. He developed methods and techniques for amplifying the principles contained in the aphorisms and their corollaries, and called it Vedic Mathematics. According to him, there has been considerable literature on Mathematics in the Veda-sakhas. Unfortunately most of it has been lost to humanity as of now. This is evident from the fact that while, by the time of Patanjali, about 25 centuries ago, 1131 Veda-sakhas were known to the Vedic scholars, only about ten Veda-sakhas are presently in the knowledge of the Vedic scholars in the country. The Sutras apply to and cover almost every branch of Mathematics. They apply even to complex problems involving a large number of mathematical operations. Application of the Sutras saves a lot of time and effort in solving the problems, compared to the formal methods presently in vogue. Though the solutions appear like magic, the application of the Sutras is perfectly logical and rational. The computation made on the computers follows, in a way, the principles underlying the Sutras. The Sutras provide not only methods of calculation, but also ways of thinking for their application.

• III.    Proposed architecture

The proposed 4 bit multiplier, gives an 8 bit product (P=A*B), where A and B shall be unsigned numbers. The multiplier is of type Vedic-Array multiplier with bit-pair evaluation. Instead of making one straightforward multiplication as a 3 a 2 a 1 a 0 * b 3 b 2 b 1 b 0 = p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 this multiplier carries out the multiplication in two steps. First, four 2 bit multiplications carried out, creating four partial 4-bit products. The four 4-bit partial products are added together to create the final 8-bit product. Using multiplexers can do multiplication. With this method is the hardware cost kept low to implement the multiplier. Also the work to implement the multiplier can be kept low, since only three different types of non-complex blocks are needed to be used to build up the entire multiplier.

Ex:  a = 0110

b = 1010

x	0100
y	0010	Sa5	Sa0
z	0100	0 1	1 1 0 0
w	0010	w3	w0

0 0 1 0

multiplication in time O ( n ). The second type arrays are of tree form, permitting higher speed in O (log n ) time, but the irregular form of a tree-array does not permit an efficient VLSI realization. The four different partial products are created with the four multiplexers. All four inputs of the multiplexers are four bits wide. The CPA and CSA adder consists of full adders and half adders. This optimization can be carried out as part of the synthesis operation. Both CSA-adders can be implemented identically at RTL level by moving the optimization to the synthesis operation.

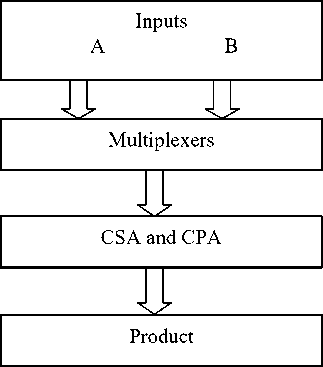
Fig 2. Block diagram of Vedic-Array Multiplier

• IV.    Synthesis and simulation result analysis

Fig 2. shows the overall components involved in the design of 4-bit Vedic-Array architecture and it is implemented in Verilog HDL. Logic synthesis and simulation are done in Xilinx ISE simulator.

The synthesis results are compared with array and booth multiplier architecture. The results are shown in Table 1. The Table shows the area, speed and power estimation for Vedic-Array, Booth and Array multiplier architecture.

Simulation waveform, RTL Schematic and Technology Schematic of Vedic-Array, Booth and Array Multiplication Techniques is shown in below figures i.e., fig 3 to fig 11.

0 0 1 1 1 1 0 0

Fig 1: How the multiplier perform the multiplication.

The overall structure of the multiplier is as shown fig2, where multiplication can be done using multiplexers, and the addition is carried out in two steps i.e., carry save addition and carry propagate addition for high speed. In this technique, intermediate results are always in a redundant form of two numbers. Two types of arrays have been proposed for the addition of the intermediate results. In the first type, the arrays are iterative with regular interconnection structure, permitting

4-bit	Area , Speed and Power
	A rea ( slices )	Speed( ns)	Power (mW)
Vedic-Array	28	3.073	57.81
Array	18	16.377	86.76
Booth	32	6.307	53.00

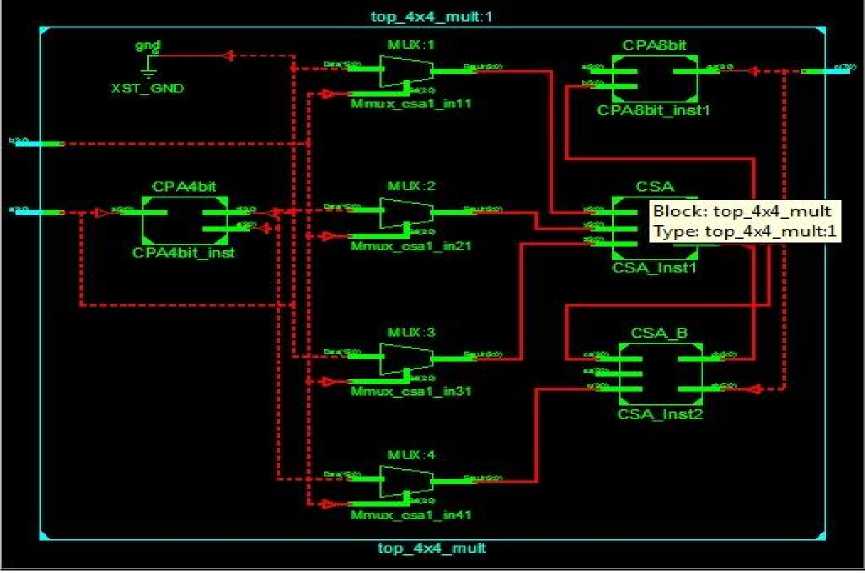
Fig 3: 4-bit Vedic-Array RTL schematic

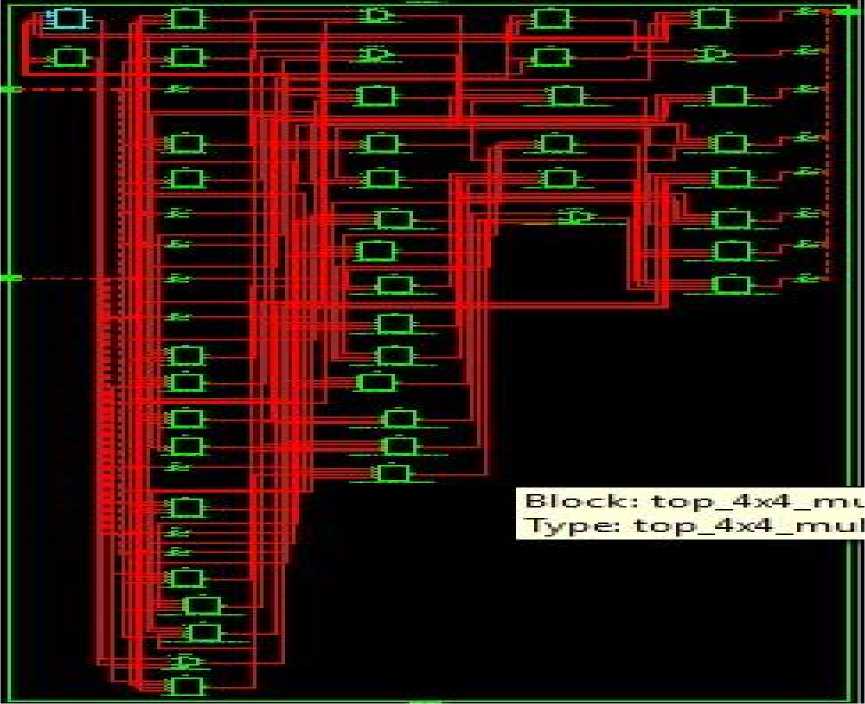
Fig 4: 4-bit Vedic-Array Technology Schematic

Fig 5: 4-bit Vedic-Array Simulation waveform

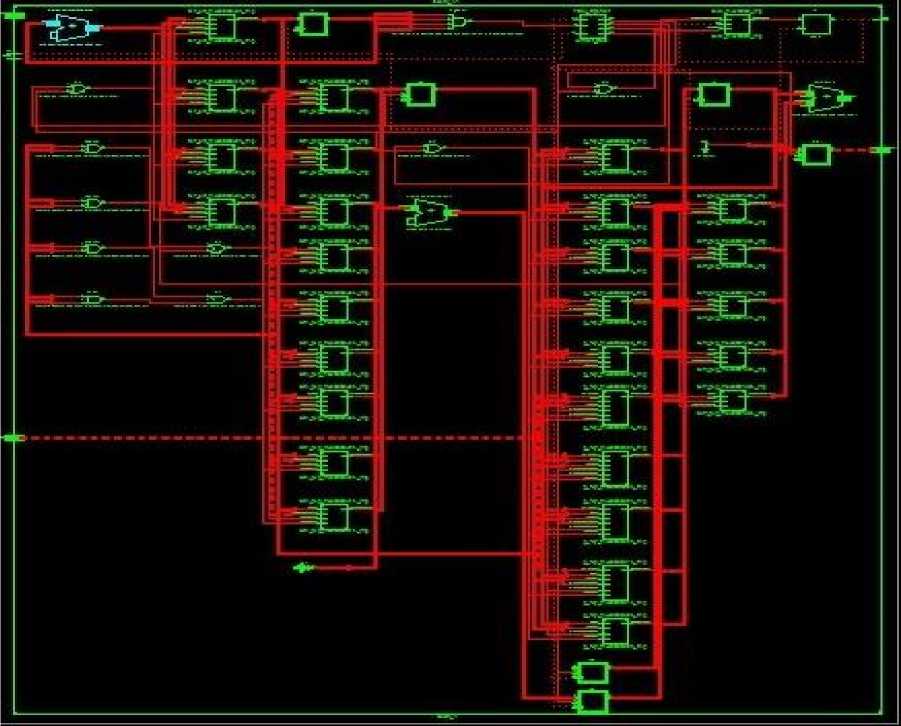
Fig 6: 4-bit Booth RTL

Vallie

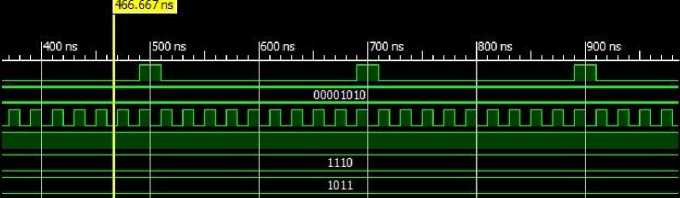
Fig 7: 4-bit Booth Simulation waveform

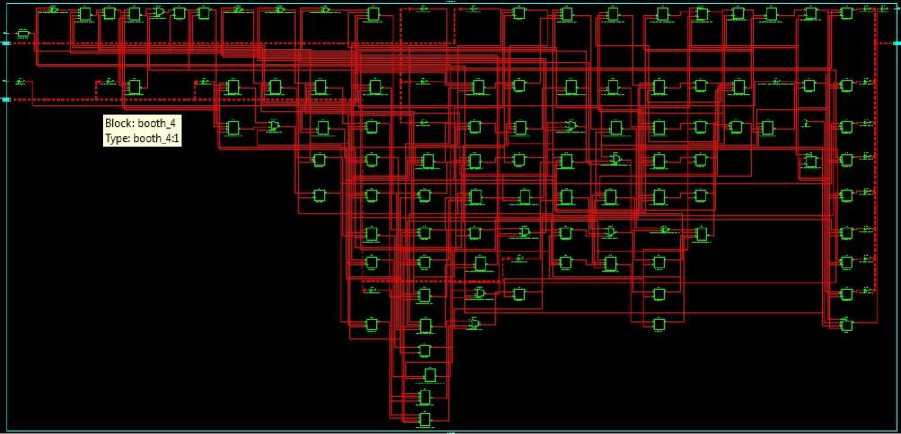
Fig 8: 4-bit Booth Tech Schematic

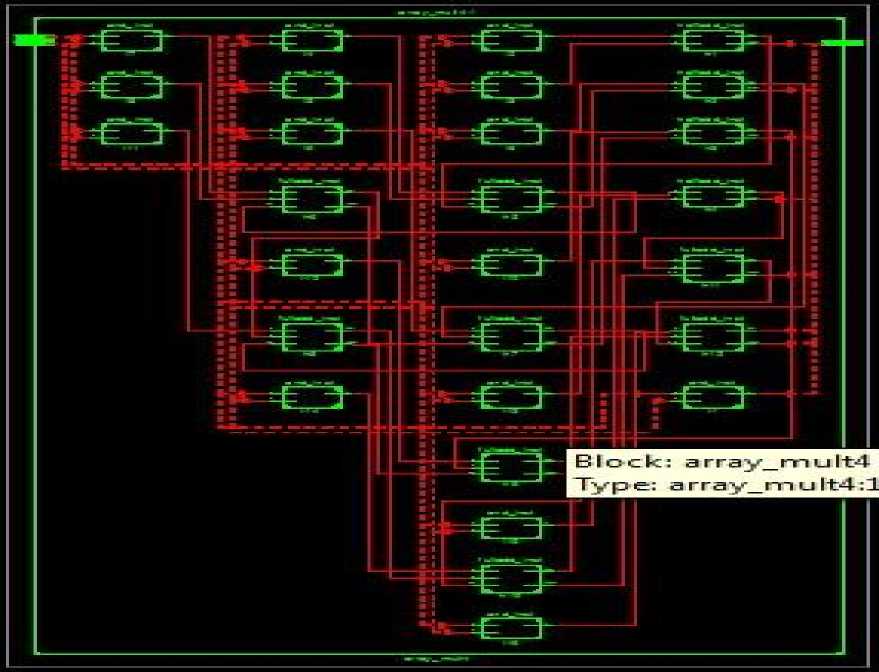
Fig 9: 4-bit Array RTL Schematic

Fig 10: 4-bit Array Simulation Waveform

Fig 11: 4-bit RTL Technology Schematic

• V.    Conclusion

The structure of this Vedic-Array maintains the same level of regularity and results show significant improvement in delay. Pipelining approach reduces the critical path and useless signal transitions that are propagated through the array. Due to its regular and parallel structure it can be concluded that Vedic-Array multiplier architecture is efficient in terms of delay and Booth multiplier is superior with respect to complexity and power consumption. However Array multiplier requires more power consumption and gives optimum number of components required, but delay for this multiplier is larger than Vedic-Array and Booth Multiplier. Hence for high-speed requirements the Vedic– Array multiplier architecture can be applied, for low power requirement Booth’s multiplier is suggested. Due to its structure, it suffers from a high carry propagation delay in case of multiplication of large number. Further the work can be extended for optimization of said multiplier to improve the power or to minimize the area. The idea of proposed hybrid multiplier architecture here may set path for future research in this direction. Future scope of research is to reduce power and area requirements.