Plane-strain extrusion of a green type porous plastic material through a wedge-shaped die
Автор: Sevastyanov G.M.
Статья в выпуске: 2, 2022 года.
Бесплатный доступ
This paper presents the solutions for the plane-strain extrusion of porous material. We consider the problem of a stationary plastic flow through a wedge shaped die. We neglect friction between the die and the deformed material since it is rather a negative effect and should be avoided in manufacturing. The elliptic Green type yield condition and its piecewise-linear approximation are adopted for this problem. In the last case, we obtain analytical solution that links extrusion pressure and area reduction to the initial and final density of the porous material. For elliptic Green yield condition the problem reduced to nonlinear ODE that integrated numerically. The results are compared with known solution for Gurson model. The extrusion pressure predicted by the piecewise-linear model is lower than what obtained by the elliptic Green model. In turn, the pressure predicted by elliptic Green model is lower than the pressure obtained in the frame of Gurson model. At low values of area reduction, all three models predict approximately the same extrusion pressure. With a small initial porosity of the material, the Gurson model gives results that are close to the elliptic Green model, and with a large initial porosity, to the piecewise-linear Green model.
Porous solids, plasticity, green type yield condition, gurson criterion, plane-strain condition, wedge-shaped die
Короткий адрес: https://sciup.org/146282472
IDR: 146282472 | УДК: 539.374 | DOI: 10.15593/perm.mech/2022.2.01
Текст научной статьи Plane-strain extrusion of a green type porous plastic material through a wedge-shaped die
PNRPU MECHANICS BULLETIN
This paper presents the solutions for the plane-strain extrusion of porous material. We consider the problem of a stationary plastic flow through a wedge shaped die. We neglect friction between the die and the deformed material since it is rather a negative effect and should be avoided in manufacturing. The elliptic Green type yield condition and its piecewise-linear approximation are adopted for this problem. In the last case, we obtain analytical solution that links extrusion pressure and area reduction to the initial and final density of the porous material. For elliptic Green yield condition the problem reduced to nonlinear ODE that integrated numerically. The results are compared with known solution for Gurson model. The extrusion pressure predicted by the piecewise-linear model is lower than what obtained by the elliptic Green model. In turn, the pressure predicted by elliptic Green model is lower than the pressure obtained in the frame of Gurson model. At low values of area reduction, all three models predict approximately the same extrusion pressure. With a small initial porosity of the material, the Gurson model gives results that are close to the elliptic Green model, and with a large initial porosity, to the piecewise-linear Green model.
Extrusion is a valuable technological process that has long been used for continuous metal processing as well as in pharmacy and food industry [1–3].
When the die walls are smooth enough and the taper angle is small, a radial flow of the material is realized during extrusion. Plane strain radial plastic flow is one of the classical problems in the theory of plasticity. The first known solution was obtained by Nadai [4], who determined the stress field in an ideal plastic material. The stationary velocity field corresponding to this solution was found by
Hill [5] and, independently, by Sokolovsky [6]. Sokolovsky also found a complete solution to the problem for the material with power-law hardening according to the Hollomon equation. The result of Durban and Budiansky [7] is obtained for linear-hardening material (Ludwik equation). Haddow and Danyluk obtained an elastic-plastic solution of the same problem for non-hardening material in the framework of the Prandtl – Reuss theory [8]. Some other analytical and numerical results can be found in [9–12]. All the mentioned results were obtained for plastically incom-


Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International
License (CC BY-NC 4.0)
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)
pressible materials. Plastically compressible (porous) materials can be described by the classical Mohr – Coulomb, Drucker – Prager, or Mises – Schleicher yield conditions. Although the associated plasticity for these yield conditions can leads to known discrepancies between the calculated volumetric strain and the experimental one, they often used to construct the models of complex media on the base of micromechanical solutions [13–15]. More precise yield conditions (for example, Green type models [16] and Gur-son model [17]) are explicitly depend on the relative density (or porosity) of the material. For the Gurson model, an approximate analytical solution (of the first order in porosity) for stationary plane-strain radial plastic flow is known [18]. The Gurson model is also utilized to analyze plane-strain extrusion in [19–21]. Numerical results for the anisotropic model are presented in [22]. For Green type models, a number of results for axisymmetric extrusion were presented [23–25]; also the analytical solution [26; 27] for equal channel angular extrusion can be mentioned.
The present paper provides the solutions to the planestrain problem of a stationary plastic flow through a wedge shaped die (Fig. 1). For the piecewise-linear Green type criterion, an exact analytical solution is obtained. For elliptic Green yield condition the problem reduced to nonlinear ODE that integrated numerically. As in [18; 28], friction between the die and the deformed material is neglected since it is rather a negative effect and should be avoided in manufacturing. The results are compared with solution [18] for Gurson model.
V - ( p v ) = -dp/d t = 0.
is satisfied, where t is the time, p is the dimensionless density of the porous material (the value p = 1 corresponds to a d 1 d d . , porosity-free material), V = er--+ e--+ ez — is the dr ф r дф dz
Hamiltonian. Hence, for the problem under consideration, it follows that rp vr = const. (1)
From (1) it follows that
D
L = —
D фф
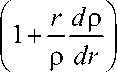
The equilibrium equation r (доrr /dr) + оrr - офф = 0 with respect to (2) takes the form p^ ° '■■ .(3)
dp l + 1
From (2) it also follows that density distribution obeys the equation rout out 1
r j L (p) +1 p •
2. Green type elliptic yield criterion
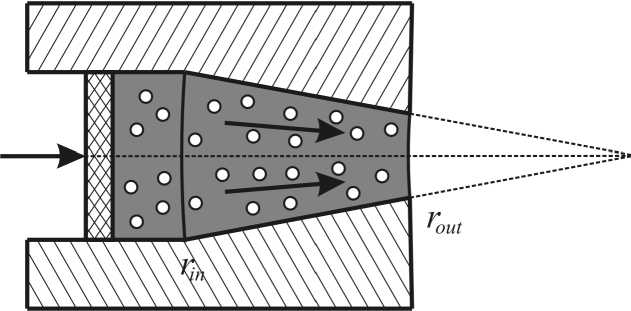
Fig. 1. Plane-strain extrusion through a wedge-shaped die
We utilize the elliptic Green yield condition and the associated flow rule
Ф= ( °/° 5 ) 2 + (V T 5 ) 2 - 1 = 0,
D = ЛдФ/д о .
where functions т 5 ( p ) and о 5 ( p ) are shear and volumetric plastic moduli, respectively; a = tr о/ 3 is the mean stress, т is the shear stress intensity, т 2 = tr о 2/ 2 - tr 2 о/6 , о is the (macroscopic) Cauchy stress tensor, Л is a scalar plastic multiplier.
From (5) it follows that (see Appendix A)
1. Plane-strain radial flow
о = D + 3 I tr D
V2т 5 Vtr D 2 + 3 tr 2 D ’
The problem with cylindrical symmetry is considered. The radial flow is described by velocity vector v = vr e r , vr < 0 . It is assumed that the cylindrical surface r = r 0 is a free boundary (see Fig. 1).
The strain rate tensor has the following form
where I is the unit tensor, 3 = ( о 5 /т 5 ) 2 /2 - 1(3 . Hence
о -о rr фф
V2т 5
1 -X
1 - L
L 2 + 2 X L + 1
D =
V® v ) T + ( V® v )
о rr =- 1 L + X
V2т 5 Vi-X V L 2 + 2 X L + 1,
d v v
= —- e ® e + — e ® e d r r r r ф ф '
For stationary flow, the continuity equation where X = 3(1 + 3) .
Substituting (6) into (3), one can obtain nonlinear first-order ODE that determines the function L(p). Boundary condition L (pout ) = -X(pout) is according to (6) since the surface r = rout is traction-free, i.e. оrr (rout) = 0 .
With calculated L ( p ) , formulas (4) and (6) determine density and pressure in the channel.
3. Green type piecewise-linear yield criterion
Under the plane-strain condition, the following piecewise-linear criterion can be utilized:
ф (о -о 3Ж2т,) + ° + °1/(2о5) -1 = 0 . (7)
Here о 1 and о 3 are the largest and smallest eigenvalues of the stress tensor, respectively. In the problem under consideration it is reasonable to assume that о 1 = о rr , о 3 = ° фф , о 1 + о 3 < 0 and according to (7) the following is obtained
where к is the shear yield stress of a porosity-free material.
-
Fig. 2 shows the dimensionless extrusion pressure P] к ,
where P = - о , versus area reduction R = 1 - r^Jr,, rr ou n rr n calculated according the obtained solutions for different values of initial density.
-
Fig. 3 shows the density of the material at the inlet of the channel, required to achieve the specified values of relative density at the outlet of the channel.
For comparison, we write down an approximate solution [18] for the Gurson model pn =1 -(1 -pout)eв “ , e Fp^
PlK = -2ln(1 -R)-(2/Л)(1 -pn)e”Sb=^d^ .
aV^ - 1
о фф
оs - тs 2тsоs
—о rr-- о 5 +T 5 о 5 +T 5
The normality rule associated with (7) leads to the expressions
D
rr
= л
о 5 -Т 52о т ss
D фф
= -л
о 5 +т 52о т ss
L (p)=D- фф
1+—^.
о 5 +т 5
and according to (4)
ln r ou t = - 1 ln P ou L + T El dp
r 2 ( P p т 5 P )
a = cosh (V3/2) , P = cosh ( V3/2 - V3ln ( 1 - R ) ) .
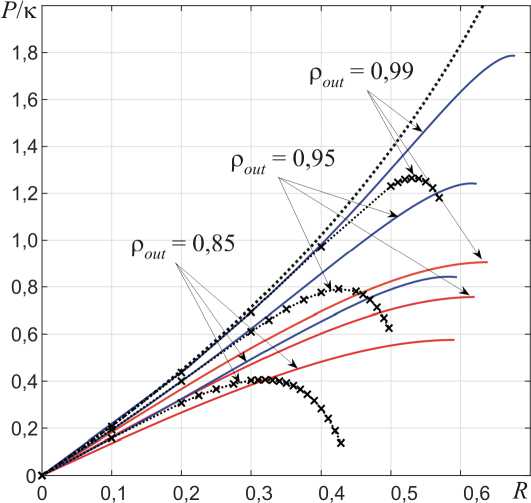
Fig. 2. Extrusion pressure and area reduction required to achieve the specified values of final density: x – Gurson model (solution [18]), blue line – elliptic Green type model (numerical solution), red line – piecewise-linear Green type model (eqs. (10) and (12)), dash line corresponds to P /K = - 2ln ( 1 - R ) (incompressible von
Taking into account the equalities (8) and (9), the equilibrium equation (3) takes the form
P^ = O rr +O ^ (11)
dp and hence
Orr =-p j" O5 ( P ) dpT- (12)
p
p
Equations (10) and (12) define the pressure distribution in the channel in a parametric form with the parameter pe [ p n , p out ] . This solution is valid for p/ n > p * , where p * can be determined from (12) with о rr ( p * ) = -о 5 ( p *) . When p n = p * , the stress state at the inlet of a channel is hydrostatic compression.
4. Results and discussion
The model [29] was utilized to determine the plastic modules:
Mises material)
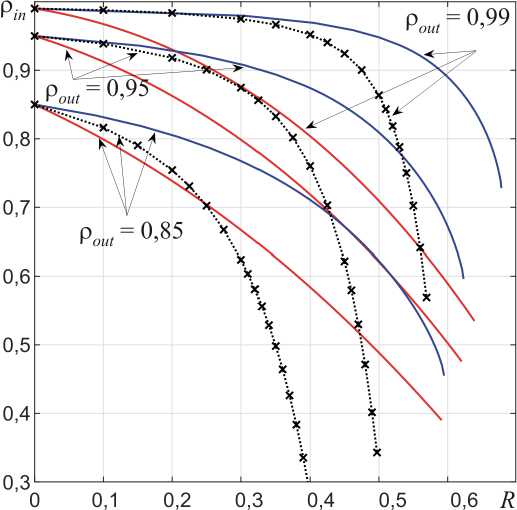
Fig. 3. Initial density and area reduction required to achieve the specified values of final density: x – Gurson model (solution [18]), blue line – elliptic Green type model (numerical solution), red line – piecewise-linear Green type model (eq. (10))
__ 2 pK _ V3pK
о 5 = V3vr-p ’т 5 = V5-2p •
It should be noted regarding the elliptic Green model and Gurson model that extrusion pressure depends nonmonotoni-cally on the area reduction R . With R above a certain value, there is a zone near the channel inlet where the pressure increases in the direction of material motion. This effect is pronounced for the Gurson model and is barely noticeable for the elliptical Green model. In addition, for both models, when area reduction is above a certain value, the compaction begins outside the tapered region.
The extrusion pressure predicted by the piecewise-linear model is lower than what obtained by the elliptic Green model. In turn, the pressure predicted by elliptic Green model is lower than what can be calculated by solution [18], obtained in the frame of Gurson model. At low values of area reduction R , all three models predict approximately the same extrusion pressure. With a small initial porosity of the material, the Gurson model gives results that are close to the elliptic Green model, and with a large initial porosity, to the piecewise-linear Green model.
Appendix A. Stress derivation for Green model
2tr σ tr D = Л---7-.
3 ст 2
and tr а = ( З ст 2 tr D )/( 2 Л ) . Substituting the last expression in (13), we express the stress tensor as
I 2 т2 а = - —7
( 3 ст 2
1 1ст> £ I +£ D J 2 Л Л
and then
а 2 = D 2 - D
Л 2
Applying the equality, we find
and then
2 т 2 tr D ( т 2
Л 2
ст 2
T tr 2 D I т 2 + 1
Л 2 I 3
21 ) 2
2 J
.
trace operator to
both sides of the last
2 т 4
tr а 2 = -^r-
Л 2
tr D 2 +I 4
( 4 т 4
- 1 I tr 2 D
3 J
For the yield condition
Ф = ( ст/ст s )2 + ( т/т s )2 - 1 = 0;
т 2 = tr 0 2/ 2 - tr 2 а /6, ст = tr а/ 3
the normality rule leads to the following expression for plastic strain rate tensor [30]
, дФ Л| 1 3 |д tr 2 а Л д tr а 2
D = Л--= — I —7--т I----+ —---- да 9 (ст 2 2 т 2J да 2 т 2 да
= Л
2 1 I tr а а
--г 1 + 3 ст 2 т 2 J 3 т 2
Applying the trace operator to both sides of equality (13), we find trZ- - tr-а=7_ [ tr D2
2 6 2 Л 2 1
tr 2 D I
3 J.
Substituting this expression together with (14) into the yield condition, we obtain the following expression for the plastic multiplier
I л । „2 11 ст2
2 — = tr D + —ztr D .
(т s J ( 2 т s
Substituting this expression into (15), after some algebra, we have а D + 3I tr D n 11 ст J
s
, V I I .
V2 т s Vtr D 2 +V tr2 D 2 (т s J 3
Список литературы Plane-strain extrusion of a green type porous plastic material through a wedge-shaped die
- Breitenbach J. Melt extrusion: From process to drug delivery technology. Eur. J. Pharm. Biopharm., 2002, vol. 54, pp. 107-117. doi: 10.1016/S0939-6411(02)00061-9
- Singh S., Gamlath S., Wakeling L. Nutritional aspects of food extrusion: A review. Int. J. Food Sci. Tech., 2007, vol. 42, pp. 916-929. doi: 10.1111/j.1365-2621.2006.01309.x
- Anferov S.D., Skul'skiy O.I., Slavnov E.V. Mathematical modelling of vegetable oil plunger extraction. PNRPU Mechanics Bulletin, 2014, no. 1, pp. 31-56. doi: 10.15593/ perm.mech/2014.1.31-56
- Nadai A. Uber die Gleit- und Verzweigungsflachen einiger Gleichgewichtszustande bildsamer Massen und die Nachspannungen bleibend verzerrter Korper. Z. Phys., 1924, vol. 30, pp. 106-138. doi: 10.1007/BF01331828
- Hill R. Mathematical theory of plasticity. 1950. Clarendon Press, Oxford.
- Sokolovsky V.V. Planar and axisymmetric equilibrium of the plastic mass between rigid walls. J. Appl. Math. Mech., 1950, vol. 14, pp. 75-92.
- Durban D., Budiansky B. Plane-strain radial flow of plastic materials. J. Mech. Phys. Solids, 1978, vol. 26, no. 5, pp. 303-324. doi: 10.1016/0022-5096(78)90002-9
- Haddow J.B., Danyluk H.T. The flow of an incompressible elastic-perfectly plastic solid. Acta Mech., 1968, vol. 5, pp. 14-21. doi: 10.1007/BF01624440
- Avitzur B., Fueyo J., Thompson J. Analysis of plastic flow through inclined planes in plane strain. J. Eng. Ind. - T. ASME, 1967, vol. 89, no. 2, pp. 361-375. doi: 10.1115/1.3610053
- Avitzur B., Choi J.C. Analysis of central bursting defects in plane strain drawing and extrusion, J. Eng. Ind. - T. ASME, 1986, vol. 108, no. 4, pp. 317-321. doi: 10.1115/1.3187082
- Alexandrov S., Mustafa Y., Hwang Y.-M., Lyamina E. An accurate upper bound solution for plane strain extrusion through a wedge-shaped die, The Scientific World Journal, 2014, vol. 2014, 189070. doi: 10.1155/2014/189070
- Alexandrov S., Kuo C.-Y., Jeng Y.-R. An accurate numerical solution for the singular velocity field near the maximum friction surface in plane strain extrusion. Int. J. Sevastyanov G.M. /Вестник ПНИПУ. Механика 2 (2022) 5-9 Solids Struct., 2018, vol. 150, pp. 107-116. doi: 10.1016/ j.ijsolstr.2018.06.006
- Thore P., Pastor F., Pastor J., Kondo D. Closed-form solutions for the hollow sphere model with Coulomb and Drucker -Prager materials under isotropic loadings. CR Mecanique, 2009, vol. 337, pp. 260-267. doi: 10.1016/j.crme.2009.06.030
- Monchiet V., Kondo D. Exact solution of a plastic hollow sphere with a Mises - Schleicher matrix. Int. J. Eng. Sci., 2012, vol. 51, pp. 168-178. doi: 10.1016/j.ijengsci.2011.10.007
- Dos Santos T., Vadillo G. A closed-form yield criterion for porous materials with Mises - Schleicher - Burzynski matrix containing cylindrical voids. Acta Mech., 2021, vol. 232, pp. 1285-1306. doi: 10.1007/s00707-020-02925-y
- Green R.J. A plasticity theory for porous solids. Int. J. Mech. Sci., 1972, vol. 14, pp. 215-224. doi: 10.1016/0020-7403 (72)90063-X
- Gurson A.L. Continuum theory of ductile rupture by void nucleation and growth: Part 1 - yield criteria and flow rules for porous ductile media. J. Eng. Mater. - T. ASME, 1977, vol. 99, pp. 2-15. doi: 10.1115/1.3443401
- Durban D., Mear M.E. Asymptotic solution for extrusion of sintered powder metals. J. Appl. Mech. - T. ASME, 1991, vol. 58, pp. 582-584. doi: 10.1115/1.2897226
- Tirosh T., Iddan D. Forming analysis of porous materials. Int. J. Mech. Sci., 1989, vol. 31, pp. 949-965. doi: 10.1016/0020-7403(89)90035-0
- Govindarajan R.M., Aravas N. Asymptotic analysis of extrusion of porous metals. Int. J. Mech. Sci., 1991, vol. 33, pp. 505-527. doi: 10.1016/0020-7403(91)90014-T
- Saleh Ch.A.R., Ragab A.R., Samy S.N. Prediction of void growth in drawing and extrusion of voided metals. Mech. Mater., 2005, vol. 37, no. 9, pp. 915-924. doi: 10.1016/j.mechmat.2004.09.004
- Kailasam M., Aravas N., Ponte Castaneda P. Porous metals with developing anisotropy: Constitutive models, computational issues and applications to deformation processing. CMES - Computer Modeling in Engineering & Sciences, 2000, vol. 1, no. 2, pp. 105-118. doi: 10.3970/cmes.2000.001.265
- Aleksandrov S.E., Druyanov B.A. Investigating the process of the steady extrusion of a compacted material. J. Appl. Mech. Tech. Phy., 1991, vol. 31, no. 4, pp. 645-649. doi: 10.1007/BF00851344
- Alexandrov S., Chesnikova O., Pirumov A. An approximate solution for axisymmetric extrusion of porous material. J. Technol. Plasticity, 2007, vol. 32, pp. 13-27.
- Sevastyanov G.M., Sevastyanov A.M. Approximate analysis of extrusion process for Green type porous material. Mech. Solids, 2021, vol. 56, no. 7, pp. 1363-1372. doi: 10.3103/S0025654421070220
- Sevastyanov G.M. Filtration in fluid-saturated poro-plastic materials during lateral extrusion. PNRPU Mechanics Bulletin, 2019, vol. 2, pp. 163-171. doi: 10.15593/perm.mech/2019.2.13
- Sevastyanov G.M., Sevastyanov A.M. Filtration and heat processes in lateral extrusion of plasticallycompressible materials. J. Phys.: Conf. Ser., 2019, vol. 1203, 012022. doi: 10.1088/17426596/1203/1/012022
- Mear M.E., Durban D. Radial flow of sintered powder metals. Int. J. Mech. Sci., 1989, vol. 31, pp. 37-49. doi: 10.1016/0020-7403(89)90117-3
- Ponte Castaneda P. The effective mechanical properties of nonlinear isotropic composites. J. Mech. Phys. Solids, 1991, vol. 39, pp. 45-71. doi: 10.1016/0022-5096(91)90030-R
- Itskov M. Tensor algebra and tensor analysis for engineers with applications to continuum mechanics. 2015. Springer International Publishing, Switzerland.


