Планирование испытаний и построение регрессионных моделей удельного импульса тяги жидкостных ракетных двигателей тягой от 10 до 420 Н

Описание двигателей S10 и S400. В EADS Astrium  вания, i – номер опыта (строки) матрицы планирова-

разработаны, прошли экспериментальную отработку и поставлены для летных испытаний двигатели S10 с тягой 10 Н и S400 с тягой 420 Н на компонентах топлива монометилгидразин (ММГ)+азотный тетраоксид (АТ). Для космических аппаратов (КА) AFRISTAR (1998), Stellat (2002), EUROSTAR 2015 (2008), Astra 1N (2011) и т. д. разработаны модификации двигателя S10-21 (рис. 1), S10-18 и S10-26 [1]. Для КА SYM-PHONIE (1975), AMOS 1 (1996), ARTEMIS (2001), Venus Express (2005), W2A (2009), Yamal 402 (2013), W3D (2013) и т. д. разработаны модификации двигателя S400-12 (рис. 2) и S400-15 [2].

Двигатели работают при номинальных суммарных массовых расходах m v ~ 3,4 г/с (S10), m _s® 125 г/с (S400) и соотношении компонентов топлива K_m ≈ 1,68 и K_m ≈ 1,61 соответственно.

Матрица планирования испытаний двигателей S10 и S400. Испытания для построения регрессионной модели 2-го порядка для удельного импульса (n – количество опытов с учетом рандомизации, N – количество неповторных опытов строки матрицы планиро- ния, mo - массовый расход окислителя, mг - массовый расход горючего) планируются по матрицам планирования испытаний ЖРДМТ S10 и S400, приведенных в табл. 1, 2.

Методика обработки результатов испытаний. Оценка параметров регрессионной модели производится по результатам испытаний, проведенных в соответствии с заданной матрицей планирования факторного эксперимента, в следующей последовательности:

• 1)    оценка воспроизводимости (ошибки опыта) и стационарности;

• 2)    расчет коэффициентов регрессионной модели и проверка их на значимость;

• 3)    проверка регрессионной модели на адекватность.

Проверка воспроизводимости и стационарности опытов. Оценка воспроизводимости производится из условия однородности дисперсий выходного параметра, определенного в разных строчках матрицы планирования:

1     ^m i                    ₂

D ⁽ y ) = ;ТТ7П⁽ y ) ср - у ^] ,      (1)

mi 1 j =1

где m – число параллельных опытов в -й строчке

1m матрицы; (yi ) =—V yi j - средняя величина вы-р mi j =1 , ходного параметра для совокупности проведенных опытов при данном сочетании факторов; yi, j – результат j -го опыта в i -й строке матрицы.

Проверка однородности дисперсий производится с помощью F-критерия. В соответствии с F-критерием дисперсии двух результатов считаются отличающи- мися статистически незначимо, если выполнено усло- вие эксп

D ( y )_max D ( y )_min

< ^F mабл ^{( а} , f max , f min ),

где F _табл – табличное значение F -критерия, т. е. предельное отношение дисперсий; а - уровень значимости, т. е. вероятность ошибочного вывода, которая в технических задачах принимается равной 0,05; fi = mi ^- 1 ^- степень свободы; D ⁽ у )_тах и D ⁽ y ) min ^-максимальное и минимальное значения дисперсий, определенных по соотношению (1).

Рис. 1. Общий вид двигателя S10-21

Рис. 2. Общий вид двигателя S400-12

Таблица 1

Матрица планирования испытаний двигателя S10

N	Случайный порядок опытов, n	m o		m г
		код	г/с	код	г/с
1	1	+	2,41	+	1,42
	6
2	8	+	2,41	–	1,09
	15
3	3	–	1,86	+	1,42
	9
4	4	–	1,86	–	1,09
	13
5	2	0	2,135	+	1,42
	12
6	10	+	2,41	0	1,255
	16
7	5	–	1,86	0	1,255
	7
8	11	0	2,135	–	1,09
	17
9	14	0	2,135	0	1,255
	18

Таблица 2

Матрица планирования испытаний двигателя S400

N	Случайный порядок опытов, n	m o		m г
		код	г/с	код	г/с
1	1	+	82,3	+	51,4
	6
2	8	+	82,3	–	44,7
	15
3	3	–	71,5	+	51,4
	9
4	4	–	71,5	–	44,7
	13
5	2	0	76,9	+	51,4
	12
6	10	+	82,3	0	48,05
	16
7	5	–	71,5	0	48,05
	7
8	11	0	76,9	–	44,7
	17
9	14	0	76,9	0	48,05
	18

Оценка стационарности также производится с использованием F -критерия:

D ( y ср )

эксп

D воспр

< ^Fтабл ^(a , fу ср , f eocnp ),

1N где у ср = n Z(y)cp

–

среднее значение выходного

параметра во всех проведенных   опытах;

1 N                ₂

D ⁽ y ср ) = _м , ^J^[ y ср   ⁽ yi ) ср ] ; D воспр

N - ¹ i =1

N

Z fD ( у .)

i =1 ________________

N

Z f

i =1

дисперсия воспроизводимости.

Расчет коэффициентов регрессии и проверка их на значимость. Расчет коэффициентов регрессии производится по методу наименьших квадратов:

где t _a - критерий Стьюдента; S_b = в^Р - среднеквадратическое отклонение коэффициентов регрессии.

Если коэффициенты взаимно коррелированы, то после исключения незначимых, остальные коэффициенты регрессии пересчитываются.

Проверка адекватности регрессионной модели. Под проверкой адекватности понимают проверку соответствия модели экспериментальным данным. Считается, что регрессионная модель адекватна исследуемому процессу, если квадраты отклонений экспериментальных точек от рассчитанных по уравнению регрессии лежат в пределах ошибки воспроизводимости.

Проверка адекватности возможна, если количество опытов хотя бы на единицу больше числа значимых коэффициентов регрессии, т. е. число степеней свободы

fад = N + nk -

N b ,

{B} = [{X}T {XI]-1 {X}T {у},

где N – число опытов в матрице планирования; n_k

–

где (например, для линейных моделей, числа входных факторов k и числа опытов n ):

число контрольных опытов; N_b

–

число значимых

{B }=

b ₀ b ₁

; { X }

x 11

x 21

" x 1 k

" x 2 k

;

{^ }=

y ₀

y ₁

.

bk

Матрица { X } T отношению к { X } .

x N 1

"' x Nk

yN

– транспонированная матрица

по

Проверка коэффициентов регрессионной модели на значимость проводится по критерию Стьюдента t при заданном уровне значимости a .

Значимые коэффициенты регрессии должны быть больше доверительного интервала A b :

b i > ^A b = t a S b ,

коэффициентов регрессии.

Оценка квадрата отклонения экспериментальных точек от модели называется дисперсией адекватности:

1 fад                           2

D ад = г ^^^[( yi ) эксп ⁽ yi ) теор ] , J ад i = 1

где ( y_i )_эксп и ( y_i )_теор – опытное и расчетное значения выходного параметра.

Дисперсию адекватности сравнивают с дисперсией воспроизводимости с использованием критерия Фишера. Для адекватных регрессионных моделей

Dад эксп                     табл ,ад , воспр , воспр где fвоспр – степень свободы для дисперсии воспроизводимости.

При неадекватности модели возможны следующие варианты решения:

• 1)    уменьшение интервалов варьирования факторов;

• 2)    перенос центра планирования эксперимента;

• 3)    использование моделей более высокого порядка.

Для планирования и обработки эксперимента было создано программное обеспечение [3].

Программа предназначена для построения планов (полного и дробного факторных экспериментов, планов Хартли и Бокса–Вилсона) для испытаний жидкостных ракетных двигателей малых тяг и построения регрессионных моделей (линейной, квазинелинейной, 2-го порядка) по результатам испытаний.

Входными данными являются: количество входных факторов, число повторных опытов, вид уравнения регрессии, число опытов в центре плана, матрица значений выходного параметра, число контрольных опытов, доверительная вероятность, кодовые значения входных факторов в контрольных опытах.

Программа позволяет проводить статистическую обработку результатов испытаний, т. е. определять число неповторных опытов плана, число коэффициентов регрессии, матрицу планирования в кодовом виде, матрицу планирования со значениями, столбец рандомизации с учетом числа повторных опытов, воспроизводимость и стационарность опытов, вектор коэффициентов регрессии, доверительный интервал для коэффициентов регрессии, адекватность регрессионной модели, расчетные значения выходного параметра в контрольных опытах.

Программа написана в математической среде Mathcad 15.0 (M020 [MC15_M020_20121127]).

Программа разделена на 2 связанных модуля: планирования испытаний и статистической обработки результатов испытаний.

Алгоритм 1 модуля планирования эксперимента в общем виде выглядит следующим образом:

• –    выбор выходного параметра;

• –    выбор количества входных факторов;

• –    назначение интервалов варьирования;

• –    выбор вида уравнения регрессии (линейная, квазинелинейная, 2-го порядка);

• –    выбор типа плана (ПФЭ, ДФЭ, план Хартли, план Бокса-Вилсона);

• –    подсчет количества коэффициентов регрессии и опытов;

• –    рандомизация;

• –    построение матрицы планирования в кодовом и размерном виде.

Алгоритм 2 модуля программы статистической обработки результатов:

• –    ввод численных значений выходного параметра;

• –    проверка опытов на воспроизводимость и стационарность;

• –    расчет коэффициентов регрессии;

• –    проверка коэффициентов регрессии на значимость;

• –    проверка модели на адекватность.

Программа имеет открытый код и может меняться в зависимости от требований: например, адаптация под другие виды двигателей или добавление других видов планов эксперимента.

Работоспособность программы проверена на нескольких испытаниях ЖРДМТ [1; 2].

Статистическая обработка результатов испытаний двигателей S10 и S400. Заполненные матрицы планирования для двигателей S10 и S400 приведены в табл. 3, 4.

После статистической обработки результатов испытаний регрессионная модель удельного импульса тяги для двигателя S10 выглядит следующим образом:

I у = 291,222 + 3,25 lh₂ + 6,875 m o m_г - 5,333 m o ², (7)

где m_г и m o - массовые расходы горючего и окислителя в безразмерном (кодовом) виде.

Таблица 3

Двигатель S10

N	Случайный порядок опытов, n	mo		m г		I уi , с	I y i , ср , с
		код	г/с	код	г/с
1	1	+	2,41	+	1,42	290	292
	6					294
2	8	+	2,41	–	1,09	274	275.5
	15					277
3	3	–	1,86	+	1,42	280	282
	9					284
4	4	–	1,86	–	1,09	291	293
	13					295
5	2	0	2,135	+	1,42	298	300
	12					302
6	10	+	2,41	0	1,255	294	295
	16					296
7	5	–	1,86	0	1,255	280	279.5
	7					279
8	11	0	2,135	–	1,09	285	286
	17					287
9	14	0	2,135	0	1,255	289	288.5
	18					288

Таблица 4

Двигатель S400

N	Случайный порядок опытов	• m o		• m г		I уi , с	I , с y i , ср
		код	г/с	код	г/с
1	1	+	82,3	+	51,4	321	319
	6					317
2	8	+	82,3	–	44,7	322	321,5
	15					321
3	3	–	71,5	+	51,4	313	312
	9					311
4	4	–	71,5	–	44,7	315	314
	13					313
5	2	0	76,9	+	51,4	318	317
	12					316
6	10	+	82,3	0	48,05	319	318,5
	16					318
7	5	-	71,5	0	48,05	314	313,5
	7					313
8	11	0	76,9	–	44,7	315	314,5
	17					314
9	14	0	76,9	0	48,05	317	316,5
	18					316

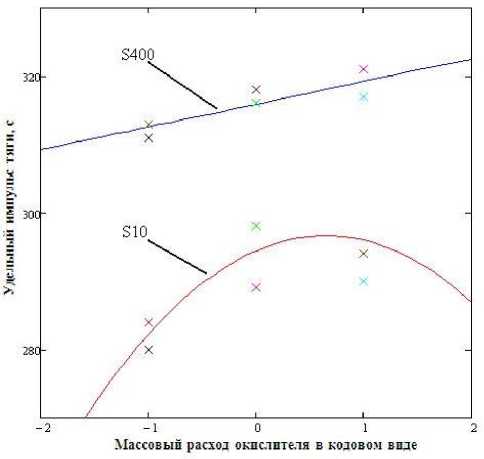
Рис. 3. Удельный импульс тяги двигателей S10 и S400 в зависимости от расхода горючего при постоянном расходе окислителя 2,41 и 76,9 г/с соответственно:

־ – расчетная модель; х – экспериментальные точки

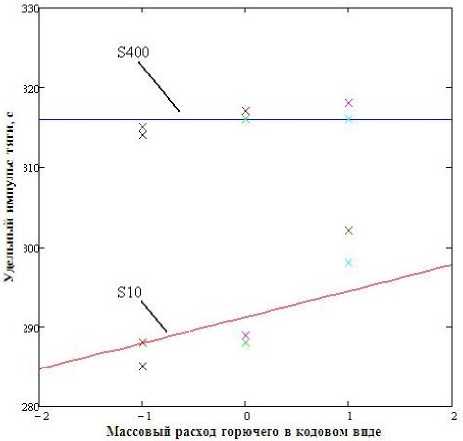
Рис. 4. Удельный импульс тяги двигателей S10 и S400 в зависимости от расхода окислителя при постоянном расходе горючего 1,42 и 51,4 г/с соответственно: ־ – расчетная модель; х – экспериментальные точки

После статистической обработки результатов испытаний регрессионная модель удельного импульса тяги для двигателя S400 выглядит следующим образом:

I у = 315,89 + 3,325 m O . . (8)

На рис. 3, 4 представлены графики удельного импульса тяги в зависимости от расхода горючего и окислителя для двух двигателей.Как видно из рис. 3, 4, с увеличением тяги влияние горючего на регрессионную модель уменьшается при одинаковом соотношении компонентов.

Проведенная апробация разработанного программного обеспечения для планирования экспери- мента и статистической обработки результатов испытаний ЖРДМТ показала его работоспособность и хорошее согласование с экспериментальными данными.