Планирование системы технического обслуживания

Эксплуатация или использование по назначению -самый длительный и ответственный период в жизненном цикле любого технического объекта, в течение которого он испытывает нагрузки различного вида и находится под воздействием внешних условий. В процессе эксплуатации проверяются технологии, методы и приемы, использовавшиеся на всех предыдущих этапах, выявляются их недостатки, проявляются скрытые дефекты конструкционных материалов, погрешности изготовления, сборки и монтажа.

Эксплуатация технической системы - непрерывный процесс, требующий планового и регулярного контроля и воздействия на объект в целом или на его составляющие и элементы, что должно обеспечивать его рабочее состояние и высокий уровень эксплуатационной надежности, который может быть обеспечен при решении двух основных задач: обеспечение нормальных режимов работы элементов и объекта в целом; прогнозирование индивидуального ресурса и назначение оптимальных регламентов эксплуатации. Решение первой задачи предусматривает разработку специальных мер, обеспечивающих снижение предельных режимов нагружения, изно са и старения, уменьшение динамических нагрузок. Решение второй задачи включает выбор оптимальной системы обслуживания, разработку системы контроля, диагностики, сбора и обработки информации о качестве функционирования, принятие оптимальных с точки зрения технико-экономических критериев различных этапов эксплуатации, повышение качества восстановления.

При планировании и оптимизации системы технического обслуживания и ремонта исходная информация может быть задана в виде функции вероятности безотказной работы P ( t ) или отказа 2 ( t ), плотности распределения наработки на отказ/( t ) или интенсивности отказов l( t ).

В зависимости от вида и назначения объекта и вида отказов для определения параметров системы технического обслуживания используются различные методы. При рассмотрении объектов, у которых возможны только явные отказы, проводится полное восстановление работоспособности. Если в предшествующем периоде отказов не было, то обслуживание проводится через интервал времени или наработки т (рис. 1). Если до момента обслуживания был отказ, после которого работоспособ- ность была восстановлена, то график технического об-

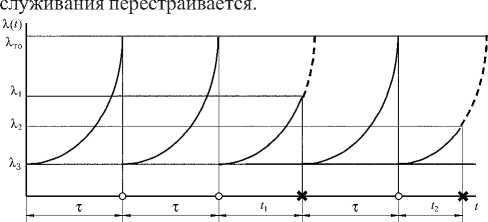
Рис. 1. Изменение интенсивности отказов при техническом обслуживании: о - техническое обслуживание; х - отказ

Считается, что проведение технического обслуживания снижает интенсивность отказов %( t ) до начального значения %₀ и тем самым повышает безотказность системы. В этом случае техническое обслуживание эффективно только при возрастающей по времени интенсивности отказов X( t ), связанных с износом, старением или накоплением повреждений элементов. При 1= const техническое обслуживание невыгодно и нецелесообразно, а при убывающей функции %( t ) техническое обслуживание даже может снижать безотказность [1].

В качестве критерия для расчета периодичности технического обслуживания может приниматься минимум средних удельных (на единицу времени) суммарных потерь от отказов и планового технического обслуживания в течение периода между восстановлениями [2]:

C( t ) = C^< t ) + C^ > т), (1) где С ₁ - средняя стоимость затрат, связанных с отказом и последующим восстановлением отказавшего объекта; С ₂ - средняя стоимость затрат, связанных с проведением планового технического обслуживания.

Если известна функция вероятности безотказной работы P ( t ) или вероятности отказа g ( t ) = 1 - P ( t ), то формулу (1) можно записать в виде

C( t ) = Cg T + C ₂[1 - 6 (т)] = C 1 [1 -P( t )] + C^P( t ). (2)

Очевидно, время работы между восстановлениями t = min{ t , т}. Следовательно, математическое ожидание времени работы будет равно

T T

M ( t _р ) = J tf ( t ) dt + т P ( t ) = J P ( t ) dt . (3) 00

Тогда средние удельные затраты можно выразить формулой

C ( t ) - Д¹" P ^1;>1' C - ^{P (t)}       ...

c с^ । ^т               ■     ⁽⁴⁾

M ⁽ t ^р )           J p ( t ) dt

Для определения значения времени или наработки т, при которых средние удельные затраты с (т) будут минимальными, необходимо производную функции (4) приравнять к нулю. После этого можно получить следующее выражение:

т

^P ( t ) +X ( t ) J Р ( t ) dt = -с— .        (5)

0             C 1 C -

При известных функциях P(t) и %(t) уравнение (5) позволяет найти оптимальную продолжительность работы объекта между плановыми техническими обслуживани-ями при явных отказах.

Если у объекта возможны только неявные отказы, то при прочих равных условиях в выражении (1) в суммарных затратах необходимо учесть дополнительные потери от скрытого отказа

T

C ( t ) = C ₁ p ( t <  t ) + С 2 p ( t >  t ) + c 3 J tf ( t- t ) dt = C ₁ [ 1 -

T

1 - P ( t ) ] + C 2 P ( t ) + c 3 J [ 1 - P ( t ) ] dt =

= C + ( C - - C 1 ) P ( t ) + c 3

t-

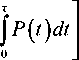
где c ₃ - средние удельные (в единицу времени) затраты. Средние удельные затраты за время т равны

^{c (t)} =t

C + ( C - - с 1 ) Р ( t ) + c 3

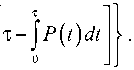
Приравняв к нулю производную выражения (7) по т, получим уравнение

^{Р (t)+t} f ^(t)- 7^3

T т-J P (t) dt

,

C 1 - с - ^,

при решении которого можно определить оптимальную периодичность технического обслуживания.

В отличие от предыдущего случая при неявных отказах объекта проведение технического обслуживания эффективно даже при постоянной интенсивности отказов, так как при этом сокращается время, в течение которого объект неработоспособен.

При оптимальном планировании индивидуального ресурса основной принцип назначения срока следующего технического обслуживания t может быть записан в виде et k +T k )= e *,                (⁹)

где t _k = t_{k +1}- t - назначенный остаточный ресурс, g * - предельно допустимое значение вероятности отказа.

Обычно при назначении периодичности технического обслуживания интервалы времени T _k уменьшаются по мере накопления повреждений в основных элементах объекта, хотя общий уровень надежности возрастает (рис. 2).

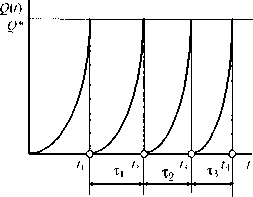
Рис. 2. Изменение вероятности отказа при техническом обслуживании

Наряду с критерием предельно допустимой вероятности отказа для определения продолжительности работы объекта между очередными техническими обслужи-ваниями используются также экономико-математические критерии. При этом требования надежности выполняют роль ограничений [1].

Например, для оптимизации технического обслуживания можно использовать целевую функцию I ( t ), равную математическому ожиданию вклада объекта в произведенную продукцию или полезный экономический эффект при ее эксплуатации на отрезке ( t , t ):

I ( t )- n ( t )- C - E ( t ), (10) где n ( t ) - разность между стоимостью произведенной продукции и ее себестоимостью (т. е. чистая прибыль); С - стоимость изделия; E ( t ) - сумма прямых и косвенных потерь из-за достижения объектом предельного состояния.

Для выбора оптимального момента проведения следующего технического обслуживания должно выполняться условие

I ( t k ^{+ т} k Н max . (11) ¹ k

По мере накопления повреждений и снижения эффективности назначенный остаточный ресурс уменьшается (рис. 3). При некотором значении t >  t_k эксплуатация должна быть прекращена из-за нарушения ограничения на вероятность отказа Q ( t ) <  g *.

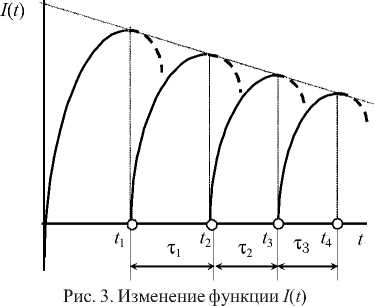
при техническом обслуживании

Оптимальную продолжительность работы между техническими обслуживаниями можно также оценивать с помощью безразмерного критерия е:

• ^е = [to I ( t k ^{+ т} k ) ] . ⁽¹²⁾

Эксплуатация объекта прекращается, когда значение параметра е становится предельным.

Решение задач оптимизации системы технического обслуживания включает, как правило, построение графа состояний, составление модели надежности и определение характеристик системы технического обслуживания. При этом обычно рассматриваются установившиеся режимы и, соответственно, стационарные модели надежности и финальные значения вероятностей нахождения объекта в каждом из возможных состояний. Определение оптимальных параметров системы технического обслуживания обычно заключается в выборе таких параметров, удовлетворяющих предъявляемым требованиям, при которых возможные потери (ущерб) и затраты на техническое обслуживание минимальны.

В период нормальной эксплуатации интенсивность отказов примерно постоянна и условие стационарности соблюдается по определению [1]. В период же приработ ки для того, чтобы отличия индивидуальных законов распределения наработок элементов мало влияли на форму потока отказов системы в целом, необходимо выполнение соотношения [1]

Mm( t )>10(X₀/ 1-1), (13) где N - число элементов в системе; m ( t ) - математическое ожидание числа отказов или неисправностей на рассматриваемом отрезке времени; 1₀ и 1 - интенсивности (параметры потоков) отказов или неисправностей в начальный момент времени и установившееся значение, соответственно.

Для проверки гипотезы о стационарности потока отказов или неисправностей можно также использовать стандартные процедуры проверки статистических гипотез, однако при интенсивности отказов или неисправностей менее 10-3-10-4 ч-1 наличие периода приработки практически не вызывает отклонений потока отказов от простейшего [1].

Например, в модели резервированного объекта с периодическим контролем технического состояния количество состояний равно шести и, соответственно, возможны переходы восьми видов (рис. 4) [3]. Если для периодического контроля объекты выводятся из работоспособного состояния, т. е. отключаются, то работоспособными являются только состояния 1 и 3 (готовности к работе двух и одного объекта) и поэтому основным показателем надежности можно считать суммарную вероятность Р ₁₃= Р ₁+ Р ₃. Если же контроль осуществляется без отключения, то работоспособными являются состояния 1 , 2 , 3 и 4 и основным показателем надежности является суммарная вероятность этих состояний Р _1-4= Р ₁+ Р ₂+ Р ₃+ Р ₄.

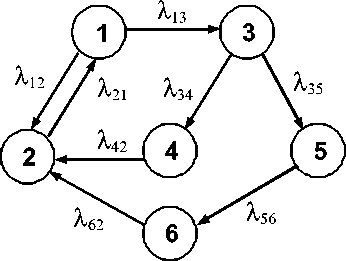
Рис. 4. Граф состояний резервированного объекта с периодическим контролем технического состояния: 1-работоспособное состояние (готовность к работе) основного и резервного объектов; 2 - периодический контроль при двух работоспособных объектах;

3 - работоспособное состояние (готовность к работе) одного из объектов; 4 - периодический контроль при одном работоспособным объектом; 5 - скрытый отказ второго объекта; 6 - периодический контроль при двух отказавших объектах

Интенсивность отказов 1, периодичность контроля t , среднее время контроля т_к и устранения отказов (ремонта) т и, соответственно, интенсивности переходов 1 1^ 1 ²1 1 ^ 1 1 и % 42 = Х б2 - ^1/(Т_к+ Т р )

могут быть получены по результатам экспериментальных исследований (испытаний) или задаются регламентом. Для нахождения интенсивностей переходов Х34 и Х56 можно воспользоваться свойствами марковских процес сов с непрерывным временем [4].

- 1

х 1 2

1 +--г ( 1 + 2 Х t , )

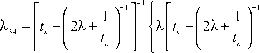
+ 1

^Х 56

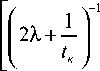
-1

2 1 + 2 Х t

К

= -- • ---------

• tK 1 - 2Х tK 2               2

Система дифференциальных уравнений для ориентированного графа состояний (рис. 4) имеет вид dPd = -(Х12 + Х„) P1 (t )+Х 21 ?2 (t);

dP y t l = Х„ P 1 ( t Н21 P 2 ( t ) +^ 42 P , ( t ) +Х„ P 6 ( t ) ;

dP^ = Х„ P 1 ( t ) - ( Х з4 + Х 35 ) P 3 ( t ) ;

dP^ = х„ P 3 ( t ) -Х„ P . ( t ) ;

d ^ = X„ P 3 ( t ) -Х„ P 5 ( t ) ;

'Pd ₌ X _I6 P ( t ) -Х б2 P 6 ( t ) .

Систему (16) необходимо дополнить нормирующим условием

P 1 ( f )+ P ₂( t ) + Р з (0 +Л(0 "^ ^{+ Р} ₆Ф ¹ (17) и начальными условиями, например

P 1 (0) - 1, P ₂(0) = Р з (0) = P ₄(0)= P ₅(0) = 0. (18)

Численный анализ системы дифференциальных уравнений (16) показывает, что при

1 < 10 5ч| переходные процессы в модели практически отсутствуют и при ее анализе можно перейти к системе алгебраических уравнений, составленных для установившегося режима и, соответственно, финальных вероятностей состояний [1]:

• ^-(^Х 12 ^+Х 1з ) P 1 ^{+ Х} 21 P 2 = 0^;

Х 12 P -Х 21 P 2 + Х .2 P . + Х б2 P 6 = 0;

Х 13 P 1 - ( Х 34 + Х 35 ) P 3 = 0;

Х 34 P 3 -Х .2 P . = 0;

Х 35 P 3 -Х 56 P 5 = 0;

,^Х56 ^P 5 ^{- Х} 62 P 6 = ^0.

Из решения системы уравнений (19) с учетом нормирующего условия (17) можно получить выражения для вероятности работоспособных состояний для двух случаев - при контроле с отключением P - P ₁+ P ₃ и контроле без отключения P _1-4 - P ₁ + P ₂ + P ₃ + P ₄:

P

,(20)

^Х 35

P - 4 = 1 -

( Л , ^Х 56

1 . ^Х 2 ■ ^Х 3 +

Х 21

262 х ,3

1 +    ^{Х 13}

з    ^Х 34 ^{+ Х} 35

^f | + ^Х 34 + ^Х 35 + ^Х 35 ' .     Х 42 Х 56 Х .

т .(21)

^Х 34 ^{+ Х} 35

Некоторые результаты расчетов представлены на рис. 5 [1].

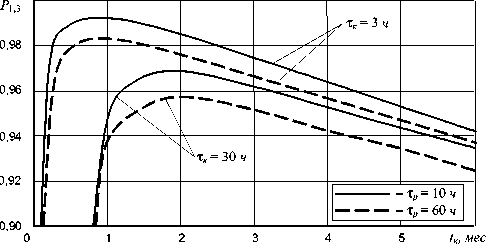
Рис. 5. Зависимость вероятности готовности резервированного объекта от периодичности контроля (Х - 10 4 ч-1)

Из анализа полученных зависимостей можно сделать следующие выводы:

• -    наибольшее влияние на вероятность P ₁₃ оказывают интенсивность отказов 1 и периодичность контроля технического состояния t ;

к’

• -    максимум значения P ₁₃ с уменьшением Х смещается в сторону больших значений t _x (при Х - 10^-4 ч^-1 он соответствует значению t 1-2 месяца, при Х - 10^-5 ч^-1 - 9-10 месяцев), график P ₁₃( t _к) при этом становится более пологим;

• -    оптимальная периодичность контроля пропорциональна его продолжительности т (например, для Х - 10^-4 ч^-1 увеличение т_к с 3 до 30 ч приводит к увеличению оптимальной периодичности с 1 до 2 месяцев, хотя максимальное значение вероятности P ₁₃ при этом снижается на 2,5 %);

• -    отклонения периодичности контроля от оптимального значения (особенно в сторону уменьшения) существенно снижают вероятность готовности объекта, особенно при больших значениях интенсивности отказов (например, для Х - 10^-4 ч^-1, т_к - 3 ч и т_р - 60 ч уменьшение ^ с 1 до 0,1 месяца снижает значение P ₁₃ на 4 % по сравнению с максимальным, а увеличение до 2 месяцев - на 1,5 %).

Эксплуатация сложных технических систем, состоящих из большого числа различных подсистем и элементов, требует различных подходов к построению системы их технического обслуживания. В результате система технического обслуживания таких объектов включает в себя несколько видов: непрерывный и периодический контроль технического состояния (диагностирование), регламентное и межрегламентное техническое обслуживание и др.