Пластический коэффициент интенсивности напряжений в задачах механики разрушения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

Одно из главных направлений развития механики разрушения, обеспечивающих ее практическое приложение, состоит в расчетно-экспериментальном исследовании параметров напряженно-деформированного состояния (НДС) в элементе конструкции или детали с трещиной. Для многих элементов машиностроительных конструкций характерной является эксплуатация в условиях циклического сложного напряженного состояния. Приложения критериев и параметров механики трещин к условиям нелинейного деформирования при сложном напряженном состоянии имеют свои особенности. В основном эффекты влияния подобных состояний реализуются через зону пластической деформации в области вершины трещины, что предопределяет необходимость построения исследований в нелинейной постановке для определения параметров состояния НДС экспериментальных образцов и реальных элементов конструкций. Известные параметры упругого и упругопластического состояния имеют ограниченные возможности воспроизведения эффектов влияния комплекса упругопластических свойств материала, геометрии тела с трещиной и условий нагружения при сложном напряженном состоянии. Приложения результатов исследований скорости роста трещин при сложном напряженном состоянии к проблемам прогнозирования остаточного ресурса элементов конструкций требует адекватных моделей накопления и развития повреждений.

Развитие нелинейной механики разрушения было основано на применении J-интеграла. Впервые понятие J-интеграла было введено Райсом [1] и Черепановым [2] с целью исследования свойств концентрации пластиче- ских деформаций в окрестности вершины трещины. Хатчинсон, Розенгрен и Райс установили связь между J-интегралом и полями НДС в вершине трещины при упругопластическом деформировании [3–5]. В качестве характеристики, описывающей НДС в упругопластической области Хатчинсоном был введен пластический коэффициент интенсивности напряжений (КИН), который непосредственно связан с J-интегралом. Полученное решение Хатчинсона–Райса–Розенгрена является классической моделью аналитического исследования состояния в пластической области вершины трещины в деформационно-упрочняющемся материале, но относится только к ситуации нормального отрыва. Шлянни-ков и Туманов распространили подход упругопластического анализа НДС в области вершины трещины в трехмерных телах конечных размеров на основе пластического КИН для условий смешанных форм деформирования [6]. В дальнейшем в ряде работ [7–15] пластический КИН использовался как параметр сопротивления росту сквозных и поверхностных трещин при сложном напряженном состоянии. Практическое приложение пластического КИН было реализовано в рамках расчета критического размера трещины в панели фюзеляжа и остаточной долговечности на стадии роста трещины диска паровой турбины [16–18].

Цель настоящей работы относится к обобщению реализованных подходов в решении задач вычислительной и экспериментальной механики трещин на основе единого параметра в форме пластического КИН, учитывающего нелинейное поведение материала, условия нагружения, вид напряженного состояния и проявление эффектов стеснения во взаимно перпендикулярных направлениях.

1. Концепция пластического коэффициента интенсивности напряжений

В соответствии с подходом Хатчинсона [3, 4] классическое решение для упругопластических полей напряжений в вершине трещины в упрочняющемся материале может быть представлено на основе J -интеграла [1,2]:

^б ₉ ⁽ г , е ) =

^аб о е ₀ I n r

- Г ( 6 ) ,

где а₀,8₀ - пределы текучести по напряжениям и деформациям при простом одноосном растяжении; r , 6 -полярные координаты, центрированные на вершину трещины; а, n - параметры упрочнения материала по модели Рамберга-Осгуда; 6 (0 ( 6 ) - безразмерные угловые функции компонент напряжений; I n - интегральный параметр, характеризующий упругопластическое напряженное состояние в области вершины трещины.

Вычисление J -интеграла по контуру, охватывающему вершину трещины в пластической области, приводит к следующему результату:

J = J ( Wdy - c jx ds ) = а ( K M ) n ^{+ 1} r<^{n + 1 )(} s ^{- 2 )+ 1} 1 „ ( 6 * ) . (2) Г

шенно четко описывает различия в напряженно -дефор -мированном состоянии в диапазоне от плоского напряженного состояния до плоской деформации.

Основным ограничением широкого применения пластического КИН в практических задачах механики трещин являлось отсутствие каких-либо решений для I n -интеграла в приложении к стандартным геометриям экспериментальных образцов. В классическом решении интегральный параметр I n является функцией только показателя деформационного упрочнения n . В работе [6] предложена численная процедура расчета I n -интеграла для реальных геометрий тел с дефектами типа трещин различной формы в плане и ориентации . В общем случае численная константа I_n ( 6 * ) является функцией безразмерных угловых распределений компонент напряжений б_у и перемещений и, и их производных. Выражение для расчета I n -интеграла, отсчитываемого от нижней в направлении верхней поверхности трещины, записывается в следующем виде:

+п

С ( 6 , M , , n, ( abw ) ) - J ^ - n ^{+ 1} ) "” cos e

-п

—

FEM   FEM б rr   I u 6

FEM                    FEM dur       -FEM  -FEM , du 6

------- —-rA Ur +-- d 6 J r6 I r        d 6

sin 6-

Подстановка выражения (1) в (2) дает б i = KMr "v (n+1)- jO )(6).                 (3)

Свойство инвариантности J -интеграла по отношению к пути интегрирования позволяет выбрать два контура, один из которых расположен в пластической области, а второй в зоне упругого деформирования, и уравнять полученные значения:

J = К^ = 062 In (Kp)n+1, (4) EE где K 1 - упругий коэффициент интенсивности напряжений для плоской задачи с прямолинейной сквозной трещиной; Е’ = E для плоского напряженного состояния (ПНС) и E’ = E/(1 - v2) для плоской деформации (ПД).

Разрешая уравнение (4) относительно пластического коэффициента интенсивности напряжений, получаем следующее выражение:

K р

K

_^аб 2 I n ( ⁶ * ) _

.

По мнению авторов [19], пластический КИН имеет фундаментальное значение в нелинейной механике трещин, подобно упругому КИН в классической механике разрушения. Принципиальным отличием пластического КИН является чувствительность к упругопластическим свойствам материала, описываемым пределом текучести п о и показателем деформационного упрочнения n . Более того, пластический КИН совер-

• ¹   ( f.E’EMfEM( . ~EEM fe™ \                 //-a

  --;(^б rr   u r    ^+б r6   ^u 6    ) ^{cos 6 ,          (6)} n + 1^x

где 9 - полярная координата; u_t , б_у - нормированные функции перемещений и напряжений. Все компоненты напряжений и перемещений, входящие в состав выражений для расчета I n -интеграла, определяются на основе численных решений методом конечных элементов.

Подобная формулировка пластического КИН справедлива для условий маломасштабной текучести, когда зона пластичности в вершине трещины на порядок меньше абсолютных размеров самой трещины. Это накладывает определенные ограничения использования пластического КИН как параметра, характеризующего НДС в вершине трещины в условиях развитой пластичности. Чтобы снять эти ограничения, необходимо использовать модифицированную форму записи выражения для расчета пластического КИН, в основу которого положена численная процедура вычисления J- интеграла, предложенная в работе [20] для условий развитой текучести.

Для условий развитой пластичности J -интеграл может быть записан в следующем виде:

Jf = -0Г J ( Wfdy ^{- б} i n j u i, x ds ) ,           (7)

E г где Г - контур обхода против часовой стрелки вокруг вершины трещины от нижнего ее берега до верхнего ; ni - единичный вектор, направленный по нормали к контуру интегрирования; перемещения в безразмерном виде определяются следующим образом:

uE ui =------.

G o w

ласти вершины трещины, определяется на основе численных решений по МКЭ согласно формуле (6).

В формуле (7) параметр плотности энергии деформирования (ПЭД) представлен в безразмерном виде:

W f =

+ v _2   1 - 2v _2     a n _„ + 1

~ ⁵ e ⁺ r   ⁵ kk ^{+    5} e

3         6         n +1

В формулах (7) и (9) тензор и инвариант напряжений нормированы на предел текучести материала

⁵ .    ⁵ j / ⁵o и ⁵ kk   ⁵ kk / 5 .

Подставляя выражение (9) для ПЭД в формулу (7), получим уравнение для вычисления J -интеграла на основе угловых функций напряжений и перемещений, полученных в результате численного решения:

. 2 + n

FEM f

₌ r G o

E J

1 + v 2 ~ ⁵ e

1 - 2 v _₂

,   ⁵ kk

a n -n +1 n + 1 e

cos 9 d 9-

+ П

^- r ⁵ o ² J

-n

d u_r  _

^{+ 5} r 9 dr

^ u⁹- ) cos 9 d 9 + d r J

+ П /

^{+ 5} 0 J I ⁵ rr

-n ^

d u_r  _

---+ 5_ru d9      ^{r 9}

^ u ⁹ ) sin 9 d 9 . d9 J

Тогда выражение для расчета пластического КИН для условий развитой пластичности записывается в сле-

дующем виде:

KP

FEM f

E '

n + 1

^aG 0 I n

где I n -интеграл – параметр, характеризующий поля упругопластических напряжений и перемещений в об-

2. Пластический КИН в задачах вычислительной механики разрушения

В задачах вычислительного плана предлагается использовать пластический КИН как параметр, описывающий проявление эффектов стеснения в трехмерных телах с трещиной. Под эффектами стеснения в механике разрушения подразумевается перераспределение напряженного состояния в области вершины трещины вследствие влияния геометрических параметров образцов или элементов конструкций и условий нагружения.

Шлянников и Захаров в ряде работ [21, 22] на основе метода конечных элементов (МКЭ) провели комплексное исследование влияния геометрии образца, условий нагружения и механических свойств материала на поведение пластического КИН. Рассматривались образцы трех типов, используемые в экспериментальной практике исследований развития трещин при смешанных формах деформирования. На рис. 1, а , б представлены крестообразные образцы с трещиной в центральной части, где различные степени смешанных форм деформирования могут быть достигнуты за счет комбинации угла наклона трещины α и вида двухосного напряженного состояния η = σ xx /σ yy . В компактном образце в виде прямоугольной пластины с односторонним боковым надрезом (рис. 1, в ) полный диапазон смешанных форм деформирования реализуется за счет изменения угла прикладываемой нагрузки по отношению к исходной плоскости ориентации трещины.

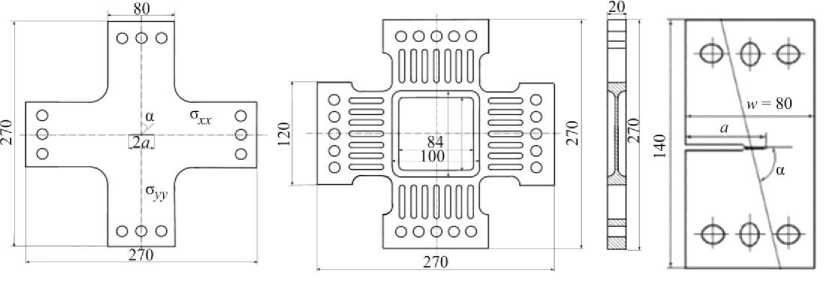
а                                    б                                в

Рис. 1. Геометрия экспериментальных образцов для смешанных форм деформирования

Fig. 1. Specimen geometries for mixed mode loading

С целью исследования влияния пластических свойств материала на поведение параметров сопротивления разрушению в полном диапазоне смешанных форм деформирования рассматривалось четыре типа материалов. В численных расчетах для описания поведения материала использовалась линейно-степенная модель по типу Рамберга–Осгуда, которая записывается в следующей форме:

5    50

£ = — + a —

EE

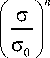
где ε – значения деформаций; σ – значения напряжений; σ 0 – предел текучести материала; E – модуль упругости; n – показатель деформационного упрочнения и α – константа модели Рамберга–Осгуда.

В табл. 1 представлены основные механические свойства рассматриваемых материалов.

Таблица 1

Основные механические свойства

Main mechanical properties

Table 1

Материал	E , МПа	σ 0 , МПа	S k , МПа	n	α
Сталь Р2М	226900	362,4	1190,0	4,131	4,141
Сталь 34ХН3МА	216210	714,4	1260,4	7,889	0,529
Алюминиевый сплав	70570	471,6	701,0	10,851	1,570
Титановый сплав Ti6Al4V	118010	885,5	1289,6	12,588	1,225

Для определения искомых нелинейных параметров сопротивления разрушению были сформированы конечно-элементные модели крестообразных образцов двух геометрий и компактного образца, содержащие сквозные трещины в виде математического разреза. Ко- нечно-элементные модели экспериментальных образцов рассматриваемой геометрии представлены на рис. 2.

В случае крестообразного образца постоянной толщины (рис. 2, а ) и компактного образца с односторонним боковым надрезом (рис. 2, в ) решалась плоская задача для классического случая плоского деформированного состояния. В областях вблизи вершины трещины и непосредственно примыкающих к ней сформировывалась регулярная сетка прямоугольных конечных элементов. Вокруг вершины трещины выполнено плавное сгущение сетки конечных элементов, в результате чего размер соответствующего конечного элемента у вершины был равен 0,02 мм. Конечно-элементные модели крестообразного образца с утонением в рабочей зоне состоят из объемных 20-узловых изопараметрических элементов. При этом, помимо сгущения сетки элементов в области вершины трещины, выполнено сгущение в точке выхода фронта трещины на свободную поверхность образца.

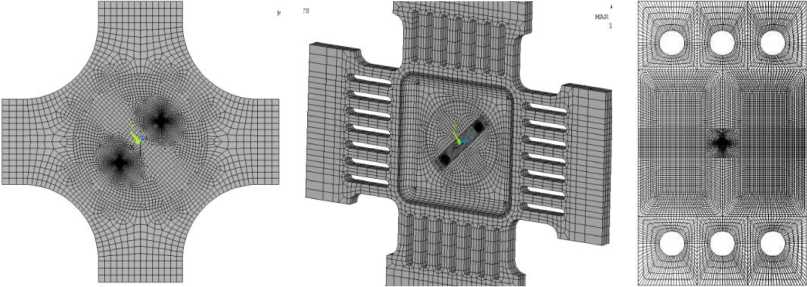
а                                    б                               в

Рис. 2. Расчетные схемы МКЭ для образцов на смешанные формы деформирования

Fig. 2. FEM models for specimens under mixed mode loading

С целью сопоставительного анализа и установления закономерностей поведения пластического КИН в образцах разной геометрии были выбраны условия нагружения, обеспечивающие постоянство параметра ПЭД в каждом образце за счет вариации сочетаний угла ориентации трещины и уровня номинальных напряжений.

В качестве количественной характеристики смешанных форм деформирования, определяющей вклад каждой моды в НДС в вершине трещины, использовался пластический параметр смешанности М р [23]. Параметр смешанности определяется как отношение окружной и сдвиговой компонент напряжений на продолжении плоскости исходной трещины:

M = — tan 1 p n aee (e = 0) ar e(e = 0)

Значения M р принадлежат диапазону от 0 до 1, где M р = 0 соответствует чистому сдвигу, а при M р = 1 реализуется форма нормального отрыва.

На рис. 3 и 4 представлены результаты, полученные авторами работ [21, 22], характеризующие влияние гео- метрии образца и пластических свойств материала на распределения нелинейных параметров сопротивления разрушению в полном диапазоне смешанных форм деформирования. На рис. 3 показаны распределения In-интеграла, характеризующего упругопластическое напряженное состояние в области вершины трещины для трех типов образцов с различными пластическими свойствами материала. На графиках распределения In-интеграла приведены в зависимости от параметра смешанности Мр.

Следует отметить, что для всех четырех типов материалов в диапазоне смешанных форм деформирования, где 0 <  М р < 0,6, значения I n -интеграла изменяются незначительно. Эффекты влияния геометрии образца и механических свойств материала на поведение пластического КИН установлены в диапазоне смешанных форм деформирования, близких к нормальному отрыву, где М р < 0,6. Диапазон смешанных форм деформирования 0,6 <  М р < 1 можно рассматривать как область перехода от одного доминантного механизма разрушения к другому.

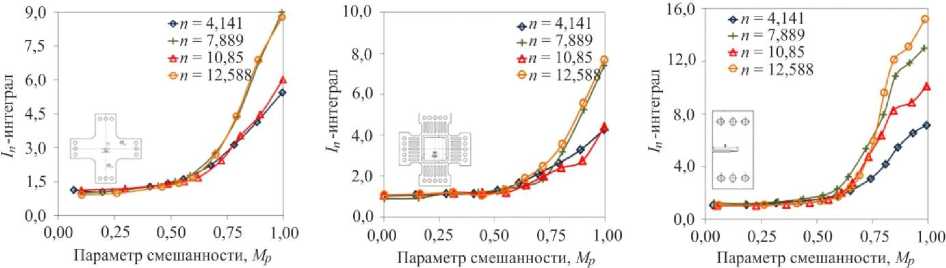
Рис. 3. Распределения I n -интеграла в зависимости от геометрии образца и условий нагружения

Fig. 3. I n -integral distributions as a function of the specimen geometry and loading conditions

На рис. 4 представлены распределения пластического КИН в полном диапазоне смешанных форм деформирования для трех геометрий образцов в зависимости от показателя деформационного упрочнения. Для всех трех типов образцов с увеличением показателя деформационного упрочнения n значения пластического КИН возрастают. В полном диапазоне смешанных форм деформирования от чистого сдвига ( М р = 0) до нормального отрыва ( М р = 1) наблюдается плавное уменьшение значений пластического КИН.

В ряде работ [7–11] пластический КИН использовался авторами для описания трехмерного напряженного состояния, реализуемого вдоль фронта поверхностных трещин. В настоящей работе приложение пластического КИН в задачах численного анализа НДС в телах с поверхностными дефектами представлено на примере полого цилиндрического образца, исследованного авто- рами в работе [9, 10]. Геометрия полого образца с односторонним боковым надрезом показана на рис. 5.

Пластический КИН вдоль фронта полуэллиптиче-ской трещины для условий нормального отрыва может быть записан в следующем виде:

1/ ( K + 1 )

K p

K i²

FEM aa IK

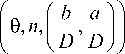
1/ ( K +1 )

A 2

a I n ( a / w )        1 1 ( a / w )

^a o J    ^а     FEM (   f ba ^

I        0 , к,      ,

^K ( A D D J

K =а/Пк- 1 ( a / w ).            (14)

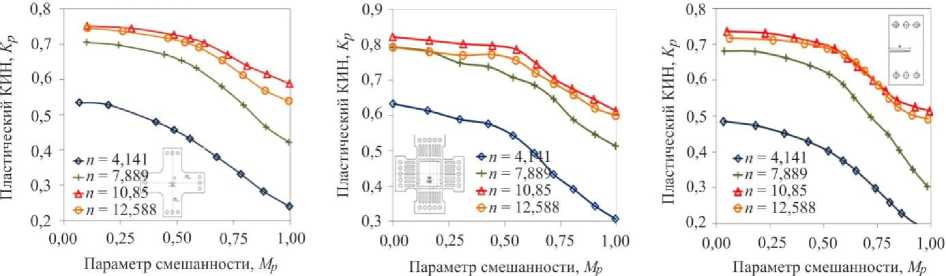
Рис. 4. Распределения пластического КИН в зависимости от геометрии образца

Fig. 4. Plastic SIF distributions as a function of the specimen geometry and loading conditions

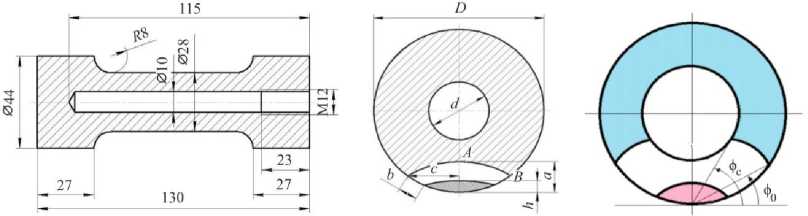
Рис. 5. Геометрия экспериментальных образцов c поверхностным дефектом

Fig. 5. Experimental specimens with a surface flaw

В подобной формулировке параметр I n -интеграл, вычисленный на основе узловых компонент перемещений и напряжений, зависит не только от пластических свойств материала, описываемых показателем деформационного упрочнения, а также от относительной длины и относительной глубины полуэллиптической трещины.

Численный анализ НДС вдоль фронта поверхностной трещины в полых образцах при одноосном растяжении проводился для двух алюминиевых сплавов Д16ЧАТ и В95АТ1 в диапазоне температур от –60 °С до +250 °С. Основные механические свойства для рассматриваемых материалов в указанном диапазоне температур представлены в табл. 2.

Таблица 2

Основные механические свойства алюминиевых сплавов

Table 2

Main mechanical properties for aluminum alloys

Материал	Температура испытаний, °С	E , МПа	σ 0 , МПа	S k , МПа	n	α
Д16ЧАТ	–60	79232	406	633	5,32	2,56
	+23	76557	438	665	5,86	1,54
	+250	75246	294	371	8,39	1,44
В95АТ1	–60	75935	506	694	7,71	1,64
	+23	75274	520	775	10,37	1,44
	+250	72737	415	436	12,00	1,22

Конечно-элементная модель полого образца с поверхностной трещиной глубиной 3 мм показана на рис. 6.

Рис. 6. Конечно-элементная модель полого образца с полуэллиптической трещиной

Fig. 6. FE model of a hollow specimen with a semielliptical crack

Для построения распределений параметров, характеризующих НДС вдоль фронта полуэллиптической трещины, были введены безразмерные координаты в следующем виде:

х 0 = Δφcosφ 0 , y 0 = Δφsinφ 0 , х c = Δφcosφ c , y c = Δφsinφ c , X i = Aфcosф i , y i = Aфsinф i , ф , e [ ф₀, ф_с ] , Аф = ф _с - ф ₀; (15)

• X, = x д = Ы , (16) x o — x c У с — У 0

R = ^7 X ₁ ² + Y ², R е [ 0,1 ] , (17)

где φ 0 – угол, определяющий положение начальной точки полиэллиптического фронта трещины; φ с – угол, соответствующий самой глубокой точке фронта трещины; φ i – угол, обозначающий текущее положение точки фронта трещины в пределах изменения от φ 0 до φ с с шагом 1°. В последующем представлении результатов будет использоваться переменная 0 ≤ R ≤ 1.

На рис. 7 представлены распределения упругих и пластических КИН, полученные в работе [9, 10], для одинаковых условий нагружения и вдоль одного и того же фронта полуэллиптической трещины в диапазоне температур. Параметры представлены в нормированных координатах R , где R = 0 – начало фронта трещины (свободная поверхность образца, точка В на рис. 5); R = 1 – точка наибольшего проникновения трещины (серединное сечение образца, точка А ).

Следует отметить, что решения для упругих КИН по определению имеют одни и те же значения для условий плоского напряженного состояния и плоской деформации и не зависят от свойств материала. В противоположность этому для одного и того же численного распределения упругого КИН по фронту трещины, вычисленного для механических свойств алюминиевых сплавов Д16ЧАТ и В95АТ1 в диапазоне температур, распределения пластического КИН значительным образом различаются. Из представленных графиков на рис. 7, б , в следует, что пластический КИН зависит от комплекса механических свойств материала и температуры испытаний. Так, по мере увеличения температуры пластический КИН принимает большие значения.

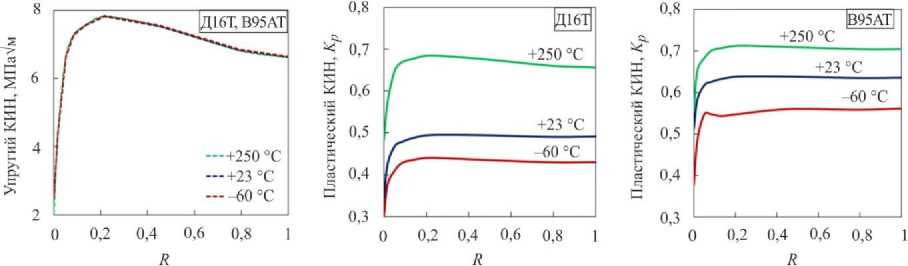
Рис. 7. Распределения упругого ( а ) и пластического ( б – Д16ЧАТ; в –В95АТ1) КИН вдоль начального фронта трещины Fig. 7. Distributions of elastic ( a ) and plastic ( b – Д16ЧАТ, c –В95АТ1) SIF along the initial crack front

Представленные в данном разделе настоящей работы данные наглядно иллюстрируют необходимость использования нелинейных параметров, учитывающих условия нагружения, влияние геометрии тела с трещиной, а также механические свойства в диапазоне температур при интерпретации характеристик сопротивления деформированию и разрушению.

• 3.    Пластический КИН в задачах экспериментальной механики трещин

В задачах экспериментальной механики трещин пластический КИН используется как параметр для интерпретации данных о развитии трещин при статическом и циклическом нагружении.

В практике экспериментальных исследований развития трещин при статическом нагружении для интерпретации данных широко используется упругий параметр в форме вязкости разрушения, K 1С , МПа√м и критическое значение J -интеграла J 1 C , МДж/м². Методы экспериментальных исследований параметров сопротивления деформированию и разрушению материалов при статическом нагружении регламентированы соответствующим международным стандартом [24].

В работе [25] предложено использовать пластический КИН в качестве характеристики сопротивления разрушению при статическом нагружении. Объектом экспериментальных исследований выступали балочные образцы при трехточечном изгибе и компактные образцы на внецентренное растяжение из легированной стали 34ХН3МА, с вариацией толщины образцов в диапазоне от 5 до 20 мм и относительной начальной длины трещины ( a / w = 0,35…0,65). Испытания образцов по определению вязкости разрушения проводились согласно международному стандарту ASTM E1820.

В рассматриваемых геометриях образцов в процессе испытаний в области вершины трещины реализуются условия нормального отрыва, поэтому пластический КИН может быть выражен непосредственно через упругий КИН на основе свойства инвариантности J -интеграла.

к, ²

- 1/ ( n + 1 )

K p

ал I™ [ 0 , n ,( a / w ),( z / B ) ] _

,

где параметр I n -интеграл является функцией пластических свойств материала, геометрических параметров образцов (относительная длина трещины ( a / w ), толщина образца ( z / B )) и условий нагружения.

Значения упругих КИН вычислялись согласно формулам, представленным в стандарте по испытаниям на вязкость разрушения:

– для балочного образца при трехточечном изгибе

P • 5

B ^; w ³²

! 1 (X),

X = a / w .

Y ( X ) =

;

2 ( 1 + 2 X )( 1 -X ) ³²

– для компактного образца на внецентренное растяжение

K ₁ = -:^} 1 (X), X = a / w , V B • w

Y( X ) =

2 + X

( 1 л ) ³'

x[ 0,886 + 4,64 X- 13,32 X ² + 14,72 X ³ - 5,6 X ⁴ ] ,  (20)

где Р – значение максимальной нагрузки, определенной в эксперименте; а – начальная длина трещины; w – ширина образца; В – толщина образца; S – расстояние между опорами в балочном образце.

Для расчета пластического КИН в образцах двух геометрий использовались значения максимальной нагрузки, определенные экспериментальным образом, и вычисленные значения I n -интеграла для каждой комбинации варьируемых параметров, толщины образца и относительной длины трещины. На рис. 8 и 9 представлены данные испытаний по определению вязкости разрушения, полученные авторами работы [25] в интерпретации по упругому и пластическому КИН. На графиках приведены результаты для двух геометрий образцов в зависимости от относительной длины трещины и толщины образца. Установлено, что максимальные упругие КИН, полученные на балочных образцах, принимают значения в диапазоне от 52 до 68 МПа√м, для компактных образцов упругие КИН варьируются в пределах от 60 до 78 МПа√м.

По сравнению с упругими, значения пластического КИН в зависимости от толщины образца и относительной длины трещины укладываются в узкую полосу разброса. Более того среднее значение пластического КИН K р = 0,61 и не зависит от геометрии образца и условий нагружения.

Приведенные результаты обосновывают применение однопараметрической характеристики сопротивления разрушению в форме пластического КИН, учитывающего эффекты стеснения во взаимно перпендикулярных направлениях. В отличие от постулатов построения двухпараметрических критериев [26–28] для учета эффектов стеснения при разрушении, не имеющих до настоящего времени реальных приложений, подход на основе пластического КИН позволил получить четкую однопараметрическую количественную оценку свойств сопротивления материала статическому разрушению, свободную от влияния геометрии тела с трещиной и условий нагружения.

Основная цель испытаний по определению скорости роста усталостной трещины состоит в установлении зависимости скорости роста трещины ( da / dN ) от параметра, характеризующего НДС в ее вершине. Традиционно такая зависимость представляется графически в виде кинетической диаграммы усталостного разрушения (КДУР), по оси ординат которой откладывается скорость роста трещины ( da / dN , мм/цикл), а по оси абсцисс упругий КИН ( K max , МПа√м). Как уже было отмечено, упругий КИН не учитывает влияние сложного напряженного состояния, реализуемого через зону пластической деформации в вершине трещины.

s

S

В = 5...20 мм

о балочный образец дД компактный образец

Д

0,3       0,4       0,5       0,6       0,7

о балочный образец д компактный образец

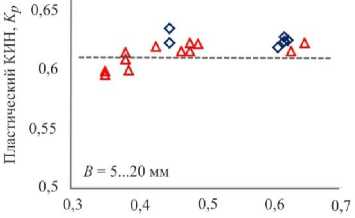
Рис. 8. Упругий и пластический КИН в зависимости от относительной длины трещины

Fig. 8. Elastic and plastic SIF as a function of a relative crack length

О балочный образец дД компактный образец

Д

О

Д Д

А

О

О a/w= 0,25...0,65 мм

о

❖

» балочный образец

Д компактный образец

Толщина образца, мм

aiw = 0,25...0,65 мм

0       5       10      15      20

Толщина образца, мм

Рис. 9. Упругий и пластический КИН в зависимости от толщины образца

Fig. 9. Elastic and plastic SIF as a function of the specimen thickness

В работе [12, 13] пластический КИН использовался для интерпретации скорости развития сквозных трещин при двухосном нагружении. Объектами исследования выступали крестообразные образцы двух геометрий: плоский крестообразный образец (см. рис. 1, а ) и крестообразный образец с утонением в рабочей зоне (рис. 1, б ). Испытания образцов проводились в условиях нормального отрыва, когда плоскость исходной трещины составляет 90° по отношению к действующим максимальным напряжениям. Различные виды двухосного напряженного состояния в диапазоне от равнодвухосного растяжения до равнодвухосного растяжения-сжатия были реализованы в эксперименте за счет приложения нагрузок во взаимно перпендикулярных направлениях λ = Рхх / Руу .

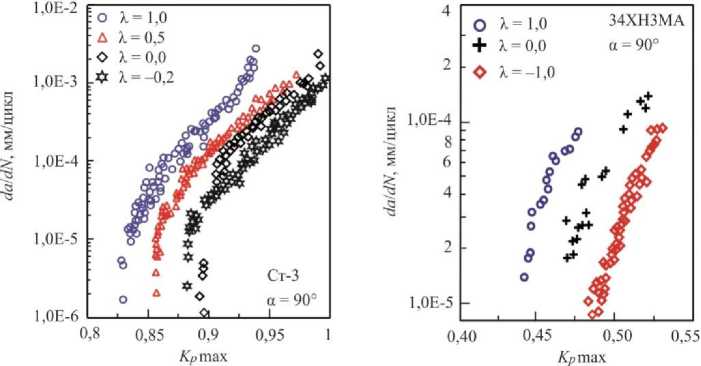
Приращение длины трещины на поверхности образцов фиксировалось с помощью оптического микроскопа МБС-10. Значения пластического КИН для каждого вида двухосного нагружения вычислялись по формуле (5) как функция относительной длины трещины Kр = f(a/w). На рис. 10 приведены кинетические диаграммы усталостного разрушения крестообразных образцов для рассматриваемых видов двухосного нагружения. Как следует из полученных результатов, в плоском образце из стали Ст-3 скорость роста трещины при равнодвухосном растяжении (λ = +1) выше, чем при остальных видах двухосного нагружения (λ = +0,5; λ = = 0; λ = –0,2). Так, по мере изменения коэффициента двухосности нагружения скорость роста трещины увеличивается от двухосного растяжения-сжатия (λ = –1) к равнодвухосному растяжению (λ = +1). Для крестообразного образца с утонением в рабочей зоне установлен противоположный характер влияния вида двухосного нагружения на скорость роста трещины.

Определенные трудности возникают в интерпретации экспериментальных данных по скорости роста трещины при смешанных формах деформирования. Трещина развивается по криволинейной траектории, которая заранее неизвестна. Траектория распространения трещины определяется видом напряженного состояния, углом исходной ориентации трещины и пластическими свойствами материала. В связи с этим для интерпретации скорости роста трещин при смешанных формах разрушения необходимо рассчитать ее траекторию развития при двухосном нагружении и для каждого промежуточного положения фронта трещины вычислить параметры, описывающие НДС в ее вершине. Авторами работы [12, 13] было показано, что пластический КИН позволяет решать эти задачи. Для достижения этой цели авторы исследовали развитие трещин в крестообразных образцах при смешанных формах двухосного деформирования.

а

б

Рис. 10. Диаграммы усталостного разрушения в интерпретации по пластическому КИН: а – для плоского образца;

б – для образца с утонением

Fig. 10. Crack growth rate diagrams in terms of plastic SIF for ( a ) flat specimen and ( b ) specimens with thinned working area

Плоские крестообразные образцы испытывались при одноосном растяжении (λ = 0) с расположением исходной трещины под углом α = 25°. На образцах с утонением в рабочей зоне был реализован классический случай чистого сдвига при равнодвухосном растяжении-сжатии (λ = –1) с ориентацией исходного надреза под углом α = 45°. Формула для расчета пластического КИН в крестообразных образцах с наклонной трещиной при двухосном нагружении записывается следующем виде:

K M ^P

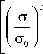
п с [1 + n- ( 1-n ) cos2a] 2 Y ² + [ ( 1 — n ) sin2a] 2 Y

4a                I „( 9, n , Mp,(a I w ) )

1I ( n + 1 )

где σ 0 – предел текучести материала; ᾱ, n – константы деформационного упрочнения материала; a / w – относительная длина трещины; η – коэффициент двухосности номинальных напряжений; α – угол исходной ориентации дефекта; Y 1 и Y 2 – K -тарировочные функции; I_n ( 9 , n , M_p ,( a I w ) ) - интегральный параметр, являющийся функцией геометрии образца с трещиной, пластических свойств материала, смешанных форм деформирования и вида нагружения.

Входящие в состав выражений для расчета пластического КИН K -тарировочные функции Y = [ a, n,( a I w ) ] , Y = [ a, n,( a I w ) ] и интегральный параметр I^F™ ( 9 , n , M_p ,( a I w ) ) в крестообразных образцах вычислялись на основе численного решения соответствующей задачи в полном диапазоне относительных длин трещины ( a / w ) = 0,1…0,7 и углов наклона трещины от 25 до 90 °С. Изменение длины развивающейся трещины при смешанных формах деформирования непрерывно связано с изменением угла наклона. Поэтому при определении искомых значений I n -интеграла и пластического КИН производилась двойная интерполяция как по длине трещины, так и по углу ее наклона, примененная в работе Шлянникова и Долгорукова [29].

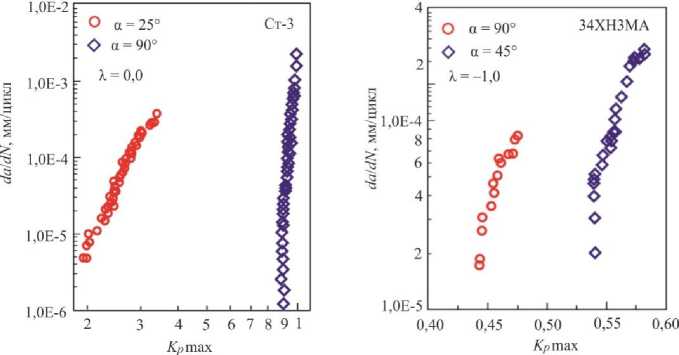
Полученные авторами работы [12, 13] диаграммы усталостного разрушения для смешанных форм двухосного деформирования показаны на рис. 11. Диаграммы усталостного разрушения, полученные для смешанных форм деформирования, представлены в сравнении с данными, полученными для условий нормального отрыва. В случае плоского крестообразного образца (рис. 11, а ) смешанные формы деформирования приводят к увеличению скорости роста трещины. Скорость роста трещины в образцах с утонением в рабочей зоне (рис. 11, б ) снижается в диапазоне от нормального отрыва до чистого сдвига.

Пластический коэффициент интенсивности напряжений K p обладает очевидным преимуществом по отношению к упругому КИН в интерпретации скорости роста трещины при смешанных формах деформирования. Пластический КИН учитывает геометрию образца с трещиной, вид нагружения и упругопластические свойства материала. Также следует отметить, что пластический КИН, являясь относительно простым в определении, учитывает вклад в развитие трещины каждой формы деформирования, что исключает необходимость использования эквивалентного параметра при интерпретации скорости роста трещины.

В работах [7–11] интерпретация развития трещин по пластическому КИН была распространена на поверхностные дефекты. Пример необходимости использования пластического КИН продемонстрирован в работе [9] при исследовании развития несквозных трещин в полых образцах в диапазоне температур. Исследования такого типа дефектов связаны с трудностями анализа упругопластического состояния в вершине трещин вдоль криволинейного фронта, а также методическими трудностями определения экспериментальных данных по скорости роста поверхностных трещин. Исследовались полые образцы с исходным надрезом полуэллип-тической формы глубиной 3 мм (см. рис. 5), изготовленные из авиационных сплавов Д16ЧАТ и В95АТ1.

Испытания образцов проводились при одноосном растяжении для трех температур (–60 °С, +23 °С и +250 °С). Основной особенностью развития поверх- ностных дефектов является одновременное увеличение размеров трещины в направлении толщины (точка А) и по свободной поверхности (точка В) полого образца.

а

б

Рис. 11. Диаграммы усталостного разрушения при смешанных формах деформирования: а – для плоского образца; б – для образца с утонением

Fig. 11. Crack growth rate diagrams under mixed mode loading for ( a ) a flat specimen and ( b ) specimens with thinned working area

а                                   б                                в

Рис. 12. Развитие поверхностной трещины в полых образцах

Fig. 12. Surface flaw propagation in hollow specimens

Авторами в работе [9] была предложена методика расчетно-экспериментального исследования развития полуэллиптической трещины в полых образцах. Существующие современные средства измерения позволили с помощью оптического инструментального микроскопа замерять приращение длины трещины на поверхности образца, как это показано на рис. 12, а. При этом увеличение размеров трещины в направлении толщины образца по циклам нагружения оставалось недоступным для прямого измерения. С этой целью через определенное количество накопленных циклов нагружения на поверхности разрушения образцов фиксировались маркерные положения фронтов полуэллиптической трещины. Это достигалось за счет изменения коэффициента асимметрии цикла нагружения при постоянном уровне максимальных напряжений. Также на каждом цикле нагружения регистрировалось раскрытие берегов трещины в месте расположения исходного надреза с по- мощью соответствующего датчика (см. рис. 11, а). На рис. 12, б представлены маркерные положения фронтов полуэллиптических трещин по циклам нагружения в полом образце при одноосном растяжении. По полученным таким способом формам фронтов трещины была экспериментально определена взаимосвязь между соотношением полуосей развивающейся трещины (а/с) и относительной глубиной проникновения трещины (а/D). Установленные экспериментальные корреляционные зависимости между относительной длиной трещины на поверхности (b/D), раскрытием берегов трещины (CMOD) и глубиной проникновения трещины (а/D) позволили получить положение, форму и размеры полуэл-липтической трещины на каждом цикле нагружения. Для дискретных положений фронтов развивающейся полуэл-липтической трещины были вычислены значения упругих и пластических КИН. Полученные на основе численных решений по МКЭ значения упругого и пластическо- го КИН для маркерных положений фронтов полуэллип-тической трещины использовались для интерпретации скорости роста трещины в полых образцах.

Контрольными при интерпретации экспериментальных данных являлись две точки фронта развивающейся полуэллиптической трещины: точка А как наиболее глубокая точка проникновения фронта трещины и точка B на свободной поверхности образца (рис. 12, в). В связи с этим экспериментальные диаграммы циклической трещиностойкости для поверх- ностных трещин представлялись именно для положения этих двух точек. На рис. 13 и 14 приведены диаграммы усталостного разрушения полых образцов из авиационного сплава Д16ЧАТ для одноосного растяжения, по оси ординат которых отложены скорость роста трещины в направлении толщины (da/dN) и на свободной поверхности (db/dN) образца, а по оси абсцисс – параметр сопротивления разрушению в форме упругого КИН (Kmax, МПа√м) и пластического КИН (Kp).

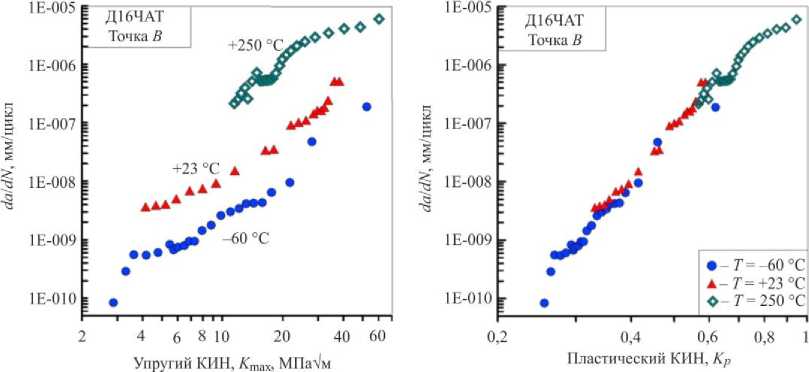
Рис. 13. Диаграммы скорости роста трещины на свободной поверхности полого образца в терминах упругого и пластического КИН

Fig. 13. Crack growth rate diagrams on free surface of the specimen in terms of elastic and plastic SIF

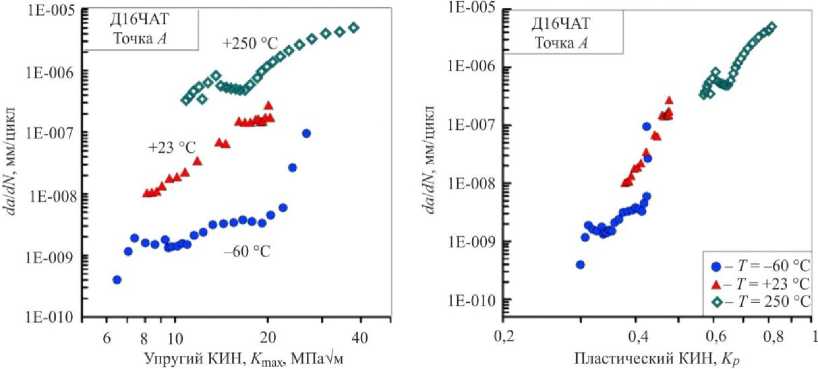
Рис. 14. Диаграммы скорости роста трещины в направлении толщины полого образца в терминах упругого и пластического КИН

Fig. 14. Crack growth rate diagrams in the thickness direction of the specimen in terms of elastic and plastic SIF

Пластический КИН в силу учета комплекса свойств исследуемого материала дает более объективную оценку сопротивления материала циклическому разрушению. Этот вывод подтверждается соответствующим положением диаграмм усталостного разрушения в зависимости от параметра интерпретации данных. При интерпретации скорости роста трещины на основе традиционного упругого КИН диа- грамма усталостного разрушения в рассматриваемом диапазоне температур представлена тремя отдельными кривыми. Напротив, при использовании пластического КИН для интерпретации тех же данных результаты отдельных испытаний для каждой температуры образуют общую кривую, состоящую из частично перекрывающихся диапазонов по скорости роста трещины.

• 4.    Прогнозирование остаточной долговечности элементов конструкций

Пример практического приложения концепции пластического КИН реализован авторами работы [16, 17] в порядке расчета долговечности на стадии роста уголковой трещины в диске паровой турбины. В рамках предложенного алгоритма расчета остаточной долговечности диска реализуется следующая последовательность действий. На первом этапе проводился анализ НДС диска от действия эксплуатационных нагрузок. В процессе эксплуатации на диск воздействуют центробежная сила от собственной массы диска, контурная нагрузка от воздействия рабочих лопаток на обод диска, которая передается через замковое соединение, кон- тактное давление на втулку диска, вызванное натягом при посадке диска на вал. Для такого сочетания условий нагружения при определении НДС диска задача решалась в трехмерной постановке с учетом нелинейного поведения конструкционного материала. На рис. 15 показаны сборный ротор паровой турбины Т-100-130 и конечно-элементная модель насадного диска 22-й ступени.

По результатам упругопластического расчета насадного диска было установлено, что в радиусных сопряжениях шпоночного паза возникают зоны локальных нелинейных деформаций, которые в процессе эксплуатации диска приводят к образованию и накоплению повреждений. На рис. 16, а показано эксплуатационное повреждение насадного диска в радиусном сопряжении шпоночного паза в виде четвертьэллиптической трещины.

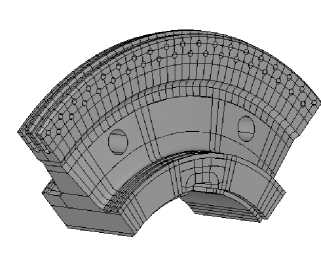
Рис. 15. Модель диска паровой турбины

Fig. 15. The power steam turbine disk model

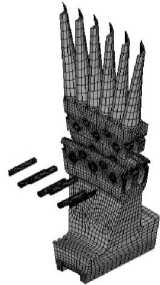
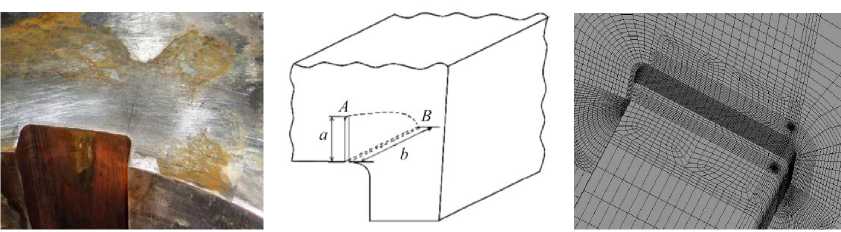
а                                   б                          в

Рис. 16. Четвертьэллиптическая трещина в шпоночном пазу диска

Fig. 16. A quarter-elliptical crack in the slot key of the turbine disk

На втором этапе оценки остаточной долговечности насадного диска состоялся анализ НДС диска с эксплуатационным повреждением в шпоночном пазу. С этой целью методом подконструкций моделировалось реальное расположение трещины в шпоночном пазу диска. На рис. 16, б представлена схема расположения поверхностного дефекта в шпоночном пазу диска. В рассматриваемом диске трещина развивается по двум направлениям: на торцевой поверхности ступицы (точка а) и на внутренней поверхности шпоночного паза по толщине ступицы (точка b). Для исследуемого диска турбины рассматривались 4 расчетные схемы шпоночного паза диска с трещинами: две расчетные схемы с чет- вертькруговыми трещинами с размерами полуосей а = b = 3 мм и а = b = 5 мм и две расчетные схемы с чет-вертьэллиптическими трещинами с размерами полуосей а = 7,5 мм и b = 10 мм, а = 10 мм и b = 20 мм.

Для всех рассматриваемых вариантов геометрий поверхностных дефектов в диске были вычислены значения упругих и упругопластических параметров НДС в вершине трещины в двух сечениях по ее фронту (рис. 17).

Для расчета остаточной долговечности диска паровой турбины на стадии роста несквозной трещины в шпоночном пазу использовалась модель, разработанная Шлянниковым [30], основанная на уравнениях ма- лоцикловой усталости, зоны процесса разрушения и скорости роста трещины. Выражение для расчета остаточной долговечности насадного диска паровой турбины на стадии роста поверхностной трещины записывается в следующем виде:

'  [    /Г —     , 2 ст 2 S_f -с 2 A S , )!

N =VJa a.   25, a ( 9 *),. n f, . th- th к (22)

fi   ^1  7 [ j     j (  ^.v.,E8y  JJ где ai – размер дефекта в направлении нормали к фронту трещины; 5=5/a - относительный размер зоны процесса разрушения нормированный на длину трещины; Sf и ASlh - критическое и пороговое значения КИН в форме плотности энергии деформирования ст*; £^ -предельные напряжения и деформации; oth - пороговое значение номинальных напряжений; о„ - номинальные напряжения; S – текущие значения КИН.

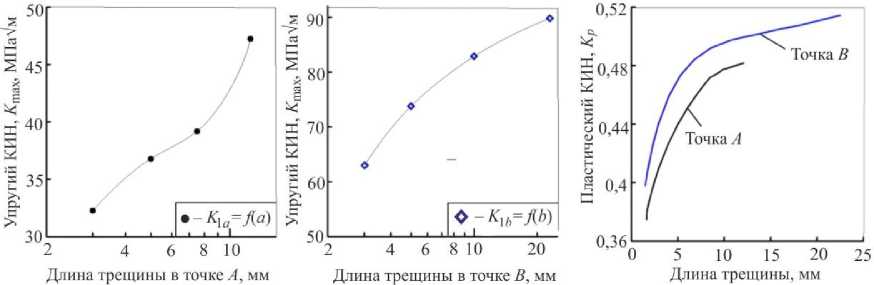
б

а

Рис. 17. Распределения упругого ( а , б ) и пластического ( в ) КИН по двум направлениям развития трещины в диске

Fig. 17. Distributions of elastic ( a , b ) and plastic ( c ) SIF for two directions of a crack propagation

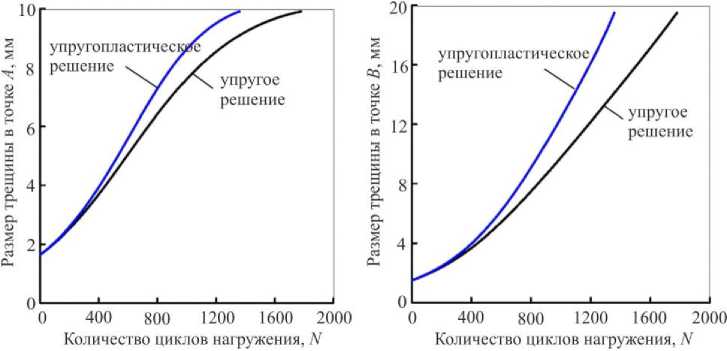
Рис. 18. Остаточная долговечность на стадии роста трещины

Fig. 18. Residual life on the crack growth stage

На рис. 18 показаны результаты расчета остаточной долговечности диска паровой турбины на стадии роста трещины. Применение в расчетах пластического КИН позволяет получить более адекватную оценку долговечности диска турбины. С точки зрения упругопластического анализа трещина на торцевой поверхности ступицы (точка а ) и на внутренней поверхности шпоночного паза по толщине ступицы (точка b ) растет быстрее по сравнению с результатами упругого решения. Пластические свойства материала оказывают значительное влияние на накопление и развитие эксплуатационных повреждений в критических зонах диска паровой турбины.

Заключение

В настоящей работе рассмотрены методы и подходы, а также результаты решения задач вычислительной и экспериментальной механики трещин, основанные на концепции пластического КИН. Показано, что параметр сопротивления разрушению материалов в форме пластического КИН является удобной характеристикой состояния в области вершины трещины при сложном напряженном состоянии, которая наиболее полно по отношению к известным параметрам учитывает комплекс упруго-пластических свойств материала, эффекты стеснения и условия нагружения. На примере экспери- ментальных образцов установлен характер совместного влияния геометрии образцов и нелинейного поведения материала на распределения пластического КИН в полном диапазоне смешанных форм деформирования.

Пластический КИН в равной степени может быть использован при интерпретации экспериментальных данных и прогнозировании предельных состояний. Установлено, что подход на основе пластического КИН позволяет получить однопараметрическую количественную оценку свойств сопротивления материала статическому и циклическому разрушению, свободную от