Пластическое деформирование материалов, чувствительных к виду напряженного состояния
Автор: Бондарь В.С., Абашев Д.Р.
Статья в выпуске: 1, 2018 года.
Бесплатный доступ
Рассматриваются основные положения и уравнения теории пластичности материалов, чувствительных к виду напряженного состояния, т.е. материалов, которые имеют различные кривые пластического деформирования при одноосном растяжении, сжатии, кручении (сдвиге). Таким образом, для таких материалов не существует единой кривой пластического деформирования при лучевых (простых) процессах нагружения. Рассматриваемая теория пластичности относится к теориям пластического течения при комбинированном упрочнении, в которой радиус поверхности нагружения принимается зависящим от первого инварианта тензора напряжений и параметра вида активного напряженного состояния, а определяющие функции эволюционного уравнения для смещения поверхности нагружения - от параметра вида добавочного напряженного состояния (состояния микронапряжений). Параметр вида определяется отношением третьего инварианта ко второму инварианту в степени 3/2 соответствующих девиаторов и равен при сжатии -1, при растяжении +1, а при сдвиге 0. В рамках этой теории рассматривается пластическое изменение объема (разрыхление) в случае зависимости радиуса поверхности нагружения от первого инварианта тензора напряжений. Для описания процессов накопления повреждений приводится кинетическое уравнение, базирующееся на работе микронапряжений на поле пластических деформаций. В этом уравнении энергия разрушения принимается зависящей от первого инварианта тензора напряжений и параметра вида состояния микронапряжений. Приводятся материальные функции, замыкающие теорию, и метод их определения. Анализируются результаты теоретических и экспериментальных исследований упругопластического деформирования образцов из алюминиевого сплава Д16Т по двухзвенным траекториям деформаций в виде «веера», а также образцов из стали 30XГСА при нагружении по двухзвенным ортогональным траекториям напряжений. Получено удовлетворительное соответствие расчетных и экспериментальных результатов. Рассмотрен эффект «расщепления деформаций», приводящий к тому, что лучевым траекториям деформаций (напряжений) могут отвечать нелучевые траектории напряжений (деформаций), а плоским траекториям - неплоские.
Пластическое деформирование, чувствительность к виду напряженного состояния, микронапряжение, неупругое изменение объема, накопление повреждений, материальные функции
Короткий адрес: https://sciup.org/146211713
IDR: 146211713 | УДК: 539.374 | DOI: 10.15593/perm.mech/2018.1.03
Текст научной статьи Пластическое деформирование материалов, чувствительных к виду напряженного состояния
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2018PNRPU MECHANICS BULLETIN
Теории пластичности, используемые в практических расчетах, от теорий течения до теории упругопластических процессов, предполагают независимость связи между напряжениями и деформациями от вида напряженного состояния. Принимается, что материал нечувствителен к виду напряженного состояния. Обычным проявлением этого является существование единой кривой деформирования при лучевых (простых) процессах нагружения. Однако некоторые материалы – технические стали, алюминиевые сплавы и т.д. – в той или иной мере имеют [1–3] различные кривые деформирования при растяжении, сжатии, кручении (сдвиге). Чувствительность этих материалов к виду напряженного состояния, проявляющаяся в скалярных свойствах, приводит к своеобразным эффектам в векторных свойствах, заключающимся в том, что лучевым траекториям в векторном пространстве [4] напряжений (деформаций) отвечают нелучевые траектории в векторном пространстве [4] деформаций (напряжений). Аналогично плоским траекториям отвечают неплоские.
Для таких материалов возможно также неупругое изменение объема (разрыхление) [5–7] особенно при циклических нагружениях. Процесс накопления повреждений при циклических нагружениях также может зависеть от вида напряженного состояния, т.е. материал может иметь различные кривые усталости при растяжении-сжатии и знакопеременном кручении [8, 9].
Попытка описать упругопластическое деформирование материалов с учетом вида напряженного состояния в рамках теории упругопластических процессов Ильюшина [4] содержится в работе Охаши [2], в которой в качестве параметра вида напряженного состояния принимается отношение третьего инварианта девиатора напряжений ко второму в степени 3/2.
В работах Е.В. Ломакина и Б.Н. Федулова [10–16] рассматривается жесткопластическая модель тела и ассоциированный закон течения с условием пластичности, зависящим от параметра «жесткости» напряженного состояния (отношения среднего нормального напряжения к интенсивности касательных напряжений). Получен ряд аналитических решений задач в условиях плоской деформации, а также численные решения на основе метода конечных элементов с учетом упругих деформаций и небольшого упрочнения (теория течения с изотропным упрочнением, включающая в себя параметр жесткости).
Ю.Г. Коротких использовал [8, 9] параметр жесткости напряженного состояния в кинетическом уравнении описания нелинейного процесса накопления повреждений.
В работах В.С. Бондаря [17–22] для описания упругопластического деформирования материалов, чувствительных к виду напряженного состояния, в рамках тео- рии течения при комбинированном упрочнении радиус поверхности нагружения зависит от первого инварианта тензора напряжений и параметра вида активного напряженного состояния (отношения третьего и второго инвариантов девиатора активных напряжений). В свою очередь, эволюционное уравнение для смещения поверхности нагружения зависит от параметра вида состояния микронапряжений (отношение третьего и второго инвариантов девиатора микронапряжений). В рамках этой теории рассматривается пластическое изменение объема (разрыхление) в случае зависимости радиуса поверхности нагружения от первого инварианта тензора напряжений. Для описания процессов накопления повреждений приводится кинетическое уравнение, базирующееся на работе микронапряжений на поле пластических деформаций. В этом уравнении энергия разрушения принимается зависящей от первого инварианта тензора напряжений и параметра вида состояния микронапряжений.
Различные подходы к учету вида напряженного состояния содержатся также в работах [23–31].
В настоящей работе рассматриваются основные положения и уравнения теории упругопластического деформирования материалов, чувствительных к виду напряженного состояния. Для описания процесса накопления повреждений приводится кинетическое уравнение накопления повреждений, учитывающее также чувствительность к виду напряженного состояния. Определяются материальные функции, замыкающие теорию, метод их определения и материальные функции для алюминиевого сплава Д16Т и конструкционной стали 30ХГСА. Анализируются результаты теоретических и экспериментальных исследований упругопластического деформирования образцов из алюминиевого сплава Д16Т по двухзвенным траекториям деформаций в виде «веера», а также образцов из стали 30ХГСА при нагружении по двухзвенным ортогональным траекториям напряжений. Проводится сопоставление расчетных и экспериментальных результатов.
-
1. Основные положения и уравнения теории упругопластического деформирования материалов, чувствительных к виду напряженного состояния
Материал однороден и начально изотропен. В процессе упругопластического деформирования в нем может возникать только деформационная анизотропия. Материал может быть чувствителен к виду напряженного состояния, т.е. иметь различные характеристики пластического поведения и разрушения при растяжении, сжатии, сдвиге. В процессе деформирования возможно как упругое, так и пластическое изменение объема материала.
Тензор скоростей деформаций представляется в виде суммы тензоров скоростей упругой и пластической деформаций
e ij =e j +e p. (1)
Упругие деформации при изменении напряжений следуют обобщенному закону Гука e ee = E [^j-v(3 ° о 8j—oi,)] , (2)
где E , v - соответственно модуль Юнга и коэффициент Пуассона.
Полагается, что в пространстве составляющих тензора напряжений существует поверхность нагружения, разделяющая области упругого и упругопластического состояний. Поверхность нагружения изотропно расширяется или сужается, смещается и изменяет форму в процессе нагружения, оставаясь выпуклой. Начальная поверхность нагружения может иметь форму, отличную от поверхности Мизеса. Уравнение поверхности нагружения принимается в следующем виде:
f ( ° -j ) = 2 ( s ij - a y )( s j — a ) -[ C p ( °« , ц - , e p • ) ] = 0.(3)
Здесь s , = s ij - a ij - девиатор активных напряжений [5]; s j - девиатор напряжений; °й = 1 1 ( 7 ° ) - первый инвариант тензора напряжений; ц , - параметр вида активного напряженного состояния; £ Up , - накопленная пластическая деформация. Тензор добавочных напряжений (остаточных микронапряжений) aij – характеризует смещение поверхности нагружения в девиаторном пространстве напряжений и является функционалом процесса нагружения. Функция Cp ( o ii , ц , , £ p , ) задает форму поверхности нагружения в зависимости от параметров, которые определяются следующим образом:
1 1 ( T a) = ° U =° \\ +° 22 +° 33 ,
Ц . = "2" I з ( D ° ) / [ 3 1 2 ( D , ) ] 2 , (4)
I 11
2 ( D ° ) = 2 s j s j , I з ( D , ) = 3 s j s jk s ki ,
2 ppp £ u , J I 3 e ij e ij I dt .
Здесь e p = e ip - e p S j - девиатор пластической деформации; e p = 3 e ip - средняя пластическая деформация. Параметр вида активного напряженного состояния ц , е [ - 1; 1 ] при сжатии равен - 1 , при сдвиге равен 0, а при растяжении равен +1.
В свою очередь, при определении добавочных напряжений aij учитывается, что процесс образования или снятия добавочных напряжений зависит от вида доба- вочного напряженного состояния, т.е. от параметра ц a вида добавочного напряженного состояния, который определяется следующим образом:
Ц a = 1 3 ( D a ) / [ 3 1 2 ( D a ) ] 2 ,
2 (5)
1 1
I 2 ( Da ) = " aj aij , I 3 ( Da ) = 3 aij ajk aki .
функцию C p ( _ , , ц * , £ Р * ) , приравнять эти выражения и разрешить относительно £ Up * . Тогда уравнение связи скорости накопленной пластической деформации и скоростей напряжений будет иметь следующий вид:
B
> _
■
_ 11
,
Таким образом, поверхность нагружения (3) зависит от первого инварианта тензора напряжений, вторых и третьих инвариантов активных напряжений и добавочных напряжений. Зависимость поверхности нагружения от первого инварианта тензора напряжений и следующее из этого пластическое изменение объема (разрыхление) материала впервые рассмотрены в работах [6, 7]. Учет же зависимости поверхности нагружения от параметров вида активного и добавочного напряженных состояний содержится в работах [17-22].
Смещение поверхности нагружения определяется уравнением
2 „Г 2 „
«у = 3 ge ! +1 3 д Е e p + g aaij J e p . . (6)
*
E **=^- q £ + g + g е£ p * nu
*
+ g aau ,
*
D _ ___ U ~
B =— q _ , n u
С U *
£ u
* p
p n je j
* , nu
*
na
* j 11 11 au = ^—Г"
2 n u
.
В случае независимости поверхности нагружения от первого инварианта тензора напряжений пластическое изменение объема будет равно нулю и уравнения для скорости накопленной пластической деформации соответственно для мягкого и жесткого нагружений будут иметь вид
■
£
p
u *
** _^3 n y _ у . р = 3 G П у £ у
E.. 2 n *: , E u * E.. + 3 G n *: .
** u ** u
Здесь g ( ц a ) , g Дц a ) , g a ( ц a ) — функции, зависящие от параметра ц a вида добавочного напряженного состояния.
Пластические деформации определяются на основе ассоциированного c выражением (3) закона течения, и тогда тензор скоростей пластической деформации будет задаваться уравнением
Условия упругого и, соответственно, упругопластического состояний, полученные из принадлежности изображающей точки поверхности нагружения (3) и положительности скорости накопленной пластической деформации, имеют вид
а f • з n «
£ Р = -d f- X = 3 - j £ p
1' а_ у -• u *
2 п *
+£ ? 5 у ,
_ U < c p ( _ и, ц * , £ p * ) U £ Up * < 0
_ и = c p ( _ ii, ц * , £ р * ) А £ р * > 0
- упругость,
(12) - упругопластичность.
* *
n =s—q n , ,у Уу 3 q ц у ’
*
nu
nn
2 у
A 2 .* *
^ =
- _ * *
27 sik sky n =--2
1 j о / * \2
— *
„ 3 S y
3 ц,---
*
2 _ u
- 3 5 ij ,
Здесь под £ р * подразумеваются выражения, задаваемые уравнениями (10), (11) или аналогичными им.
Для описания процесса накопления повреждений используется энергетический подход и кинетическое уравнение накопления повреждений будет иметь вид
*
_ _ u a ьр
* q _ £ u * , n u
а cp q ц=^, дц*
д c p q _ = я— a _ i
.
Повторяющийся индекс k в формуле (8) означает суммирование. Тензоры n j и n * являются симметричными девиаторами, в чем нетрудно убедиться, получая на основе формул (8), что п . = 0, n * = 0, n у = n ji , n * = n * . .
Пластическое изменение объема (разрыхление), следуя уравнению (9), определяется величиной накопленной пластической деформации и имеет место только в случае зависимости поверхности нагружения от первого инварианта тензора напряжений.
Для получения уравнения для скорости накопленной пластической деформации необходимо продифференцировать по времени интенсивность активных напряжений и
а 1 /7 рР a je j ю=аюа ——-,
W 0 ( _ , ц a )
ц a = 2Т 1 3 ( D a ) / [ 3 1 2 ( D a ) ] А (13)
1 1 ( T _ ) = _ 11 , 1 2 ( Da ) = j ay ay , I 3 ( Da ) = 3 а,y a i k aki .
Здесь m - мера повреждения; a - функция нелинейности процесса накопления повреждений; W o - энергия разрушения, являющаяся функцией первого инварианта тензора напряжений и параметра вида добавочного напряженного состояния, который при одноосном сжатии равен - 1 , при сдвиге равен 0, а при одноосном растяжении равен +1. Критерием разрушения материала будет достижение повреждением предельного значения, обычно принимаемого равным единице.
Учет влияния инвариантов тензора и девиатора напряжений на процесс накопления повреждений содержится в работах [8, 9, 32]. Учет же влияния параметра вида добавочного напряженного состояния на процесс накопления повреждений рассматривается в работах [17–22].
2. Материальные функции и метод их определения
Теорию пластического деформирования материалов, чувствительных к виду напряженного состояния, замыкают следующие определяющие параметры и функции, подлежащие экспериментальному определению:
E , V , g , g E , g a , C p , a , W o . (14)
Функции g , g e , g a выражаются [17-22] через параметры анизотропного упрочнения и имеют вид
g = Ea + P 'оa , gE=P Ea , ga = -P ,
П na 3„ )2
a (о a / a n ) , a n I 2 a ij a ij \ .
Итак, теорию пластического деформирования материалов, чувствительных к виду напряженного состояния, замыкают следующие материальные функции, подлежащие экспериментальному определению:
-
Е , v - упругие параметры (модуль Юнга, коэффициент Пуассона);
Ср ( о ii , ц , , £ р , ) - функция изотропного упрочнения;
E a ( ц a ) , о a ( ц a ) , р ( ц a ) - параметры анизотропного упрочнения;
-
n a - параметр нелинейности процесса накопления повреждений;
Wo ( о й , ц a ) - энергия разрушения.
Для описания зависимости функции изотропного упрочнения от вида активного напряженного состояния предлагается следующая аппроксимация:
Ср = СР (£Р,)+[Ср+ (£Р.)— СР (вР.) ] Ыn, (16)
где С р + ( е р , ) , С р ( е UP , ) - функции изотропного упрочнения соответственно при одноосных сжатии-растяжении и кручении; n – показатель степени. Для ряда конструкционных сталей n = 3 , а для цветных сплавов n = 5 . Эти значения получены при обработке экспериментальных данных работы [2]. Для параметров E a , о a , Р , W o принимается такая же, как и (16), аппроксимация:
E a = E p + ( Ea -+- E o )|ц a|n , о a = о a + ( о -+-о р )|ц o|n , (17)
Р=Р o + ( Р-+-Р o > a|" , Wo = W o + ( W —+ — W o ) In aT . (18)
Здесь A V, о - + , P-+ , W o и E o , о a , P o , W o - параметры анизотропного упрочнения и энергия разрушения соответственно при одноосных сжатии-растяжении и кручении. В уравнениях (16) и (18) пренебрегается зависимостью поверхности нагружения и энергии разрушения от первого инварианта тензора напряжений. В противном случае все перечисленные выше параметры, соответствующие сжатию-растяжению и кручению, будут функциями первого инварианта тензора напряжений.
Для определения материальных функций проводятся такие же базовые испытания, как и для теории упругопластического деформирования [17–22], но отдельно в условиях одноосного растяжения-сжатия и одноосного кручения. Далее на основе расчетно-экспериментального метода определяются функция изотропного упрочнения, параметры анизотропного упрочнения и энергия разрушения при растяжении-сжатии ( ц , =± 1, ц a =± 1 ) и при кручении ( ц , = 0, ц a = 0 ) Для определения показателей степеней n и m в уравнениях (16)–(18) необходимы такие же базовые испытания, но по лучевым траекториям напряжений в условиях двухосного напряженного состояния при ц , =ц a * 0 и ц , =ц a ^ ± 1. Если данных таких испытаний нет, то в первом приближении можно принять n = т = 3 для конструкционных сталей и n = т = 5 для цветных сплавов. Параметр нелинейности процесса накопления повреждений n a определяется из опытов на двухблочное циклическое нагружение и практически для всех конструкционных сталей и сплавов n a = 1,5.
В табл. 1 приводятся параметры анизотропного упрочнения Ea , Р , о a для стали 30ХГСА [3] и алюминиевого сплава Д16Т [1]. Модуль Юнга для стали равен 2 - 105 МПа, а для алюминиевого сплава - 0,7 - 105 МПа. Коэффициент Пуассона для всех рассматриваемых материалов принимался равным 0,3. Параметры анизотропного упрочнения стали одинаковы для растяжения-сжатия и кручения. Для алюминиевого сплава в табл. 1 дано значение о +— при растяжении-сжатии, а при кручении ооа = 65 МПа.
Таблица 1
Параметры анизотропного упрочнения
Anisotropic hardening parameters
Table 1
|
№ п/п |
Материал |
Ea , МПа |
р |
о a , МПа |
|
1 |
30ХГСА |
9000 |
200 |
70 |
|
2 |
Д16Т |
2600 |
210 |
110 |
В табл. 2–3 приведены функции изотропного упрочнения С7 / (в р , ) при растяжении-сжатии и С р ( е Ц 1, ) при кручении для стали 30ХГСА и алюминиевого сплава Д16Т.
Таблица 2
Параметры изотропного упрочнения стали 30ХГСА
Table 2
Isotropic hardening parameters of 30HGSA steel
|
p ° и * |
0 |
0,005 |
0,01 |
0,02 |
0,05 |
|
C - , МПа |
310 |
290 |
285 |
270 |
270 |
|
Cop , МПа |
290 |
270 |
265 |
250 |
250 |
Таблица 3
Параметры изотропного упрочнения сплава Д16Т
Table 3
Isotropic hardening parameters of D16T alloy
|
p ° и * |
0 |
0,005 |
0,01 |
0,02 |
0,05 |
|
с -+ C p , МПа |
350 |
335 |
320 |
310 |
310 |
|
Co p , МПа |
250 |
235 |
220 |
210 |
210 |
Конструкционная сталь 30ХГСА является умеренно чувствительной к виду напряженного состояния – отличие кривых деформирования при растяжении (сжатии) и кручении не превышает 10 %. Алюминиевый сплав Д16Т обладает значительной чувствительностью к виду напряженного состояния – отличие кривых растяжения (сжатия) и кручения достигает 40 %. Такая значительная чувствительность к виду напряженного состояния дополняется и некоторой начальной анизотропией прутков, из которых были изготовлены образцы для испытаний.
3. Исследование упругопластического деформирования материалов, чувствительных к виду напряженного состояния
Экспериментальные исследования [1] проводились при комнатной температуре на трубчатых образцах из алюминиевого сплава Д16T. Этот сплав обладает значительной чувствительностью к виду напряженного состояния – отличие кривых растяжения (сжатия) и кручения достигает 40 %. Деформирование образцов осуществлялось осевой силой и крутящим моментом, т.е. реализовывались (P, M) -опыты. На плоскости деформаций e1 e3 (e1 = е11, e3 = 2 е12 / V3) после предварительного растяжения до деформации е1 = 50 ® 0,02 (рис. 1) осуществлялся излом траекторий с углами 0= 24, 46 и 90°. Скалярные свойства алюминиевого сплава Д16T при нагружении по траекториям в виде «веера» (рис. 2) приведены на рис. 3. На этом рисунке результаты, отмеченные 1, соответствуют углу излома 24° , 2 – 46º, 3 – 90º. Результаты расчета на основе теории упругопластического деформирования с учетом вида напряженного состояния изображены сплошными кривыми, а без учета вида напряженного состояния – пунктирными. Верхняя и нижняя сплошные кривые на рис. 3 есть, соответственно, экспериментальные кривые растяжения и кручения. Результаты эксперимента изображены треугольниками, ромбами и кружками. Векторные свойства алюминиевого сплава Д16T по траекториям в виде «веера» приведены на рис. 4. Здесь такие же обозначения, как и на рис. 3, для скалярных свойств. Следует отметить, что длина траекторий деформаций s на рис. 3 и 4 соответствует длине проекции траектории на плоскость e e3 , а угол сближения ф на рис. 4 соответствует углу между вектором напряжений а(а1 = ап,а2 = 0, а3 =а12 V3) и касательной к проекции траектории на плоскости e1e3.Из рис. 3 и 4 следует, что отличие расчетных и экспериментальных результатов не превышает 10 % как по скалярным, так и по векторным свойствам.
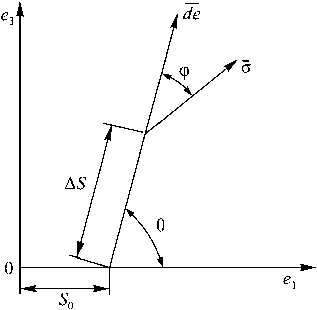
Рис. 1. Траектории деформаций в опытах И.М. Коровина Fig. 1. Deformation trajectories in I.M. Korovin’s experiments
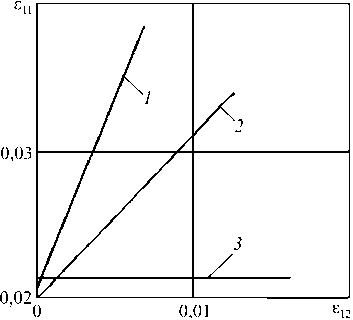
Рис. 2. Траектории деформаций в виде «веера» в опытах И.М. Коровина
Fig. 2. Beam trajectories of deformations in I.M. Korovin’s experiments
На рис. 5 приведены расчетные траектории напряжений и деформаций в векторном пространстве Ильюшина [3] для угла излома траектории деформаций в плоскости Э1Э3 на 90º. Здесь сплошные кривые соот- ветствуют расчету с учетом чувствительности материала к виду напряженного состояния, а пунктирные – без учета этой чувствительности. Экспериментальная траектория деформаций приведена быть не может, так как в работе [1] отсутствует информация о значениях компоненты деформаций £22, что позволило бы определить векторную компоненту деформаций Э2 . Следует заметить, что при обработке результатов экспериментов для получения деформации £33 обычно принимается условие несжимаемости материала.
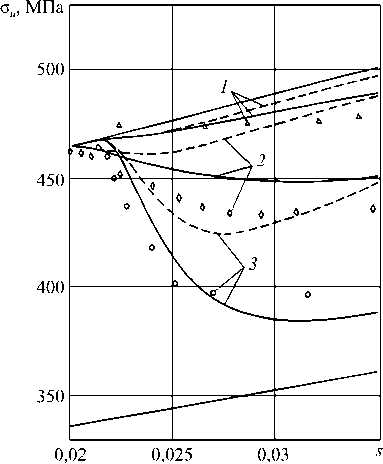
Рис. 3. Скалярное запаздывание свойств материала в опытах И.М. Коровина Fig. 3. Scalar delay of material properties in I.M. Korovin’s experiments
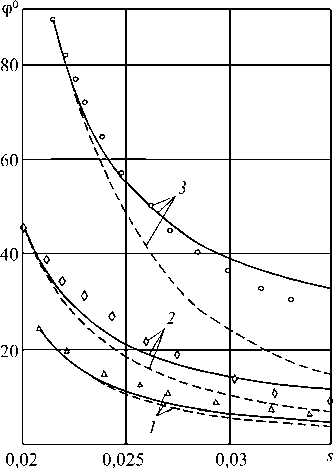
Рис. 4. Векторное запаздывание свойств материала в опытах И.М. Коровина Fig. 4. Vector delay of material properties in I.M. Korovin’s experiments
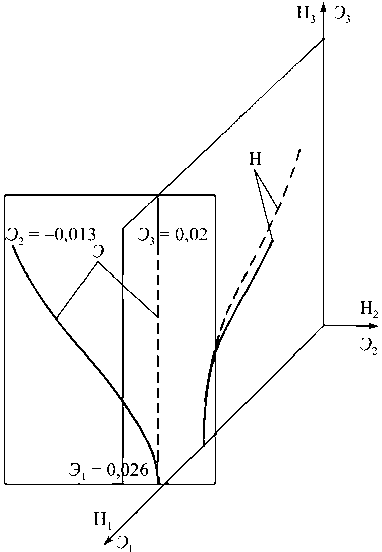
Рис. 5. Траектории напряжений и деформаций в опытах И.М. Коровина по программе 3 Fig. 5. Trajectories of stresses and deformations in I.M. Korovin’s experiments under load program 3
Анализируя полученные расчетные и экспериментальные результаты, можно сделать вывод, что «нырок» на кривых скалярных свойств для материала, чувствительного к виду напряженного состояния, значительно глубже нежели «нырок» для нечувствительных материалов. Для ортогонального излома траектории деформаций кривая скалярных свойств от кривой растяжения переходит к кривой кручения. Что касается векторных свойств, то для материалов, чувствительных к виду напряженного состояния, след запаздывания векторных свойств значительно больше следа запаздывания для нечувствительных материалов и угол сближения может принять постоянное значение, отличное от нуля. Таким образом, вектор напряжений для материалов, чувствительных к виду напряженного состояния, может не ложиться на траекторию (касательную к траектории) деформаций, и лучевой траектории напряжений может отвечать нелучевая траектория деформаций. На рис. 5 показано, как плоской траектории напряжений для алюминиевого сплава Д16Т отвечает существенно неплоская траектория деформаций, т.е. имеет место значительный «эффект Э 2 » [33].
Появление компоненты Э 2 (эффект Э 2 ) обусловлено эффектом «расщепления» деформаций [21], заключающемся в том, что на втором звене траектории деформаций при наличии на каком-либо звене кручения деформации £ 22 и £ 33 начинают отличаться друг от друга, хотя для материалов, нечувствительных к виду напряженного состояния, они остаются равными ( е 22 = £ 33 ) .
На рис. 6-8 приведены расчетные деформации £ 22 и £ 33 (штрих-пунктир, штрих-штрих-пунктир) для 1–3-й программы опытов И.М. Коровина, иллюстрирующие эффект расщепления деформаций для материала,
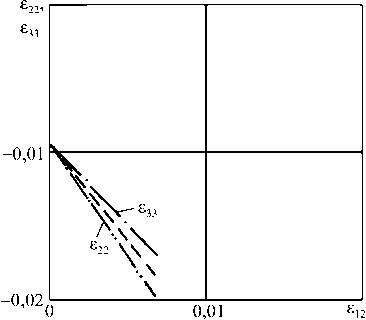
Рис. 6. Эффект расщепления деформаций в опытах И.М. Коровина по программе 1
Fig. 6. “Splitting of deformations” effect in I.M. Korovin’s experiments under load program 1
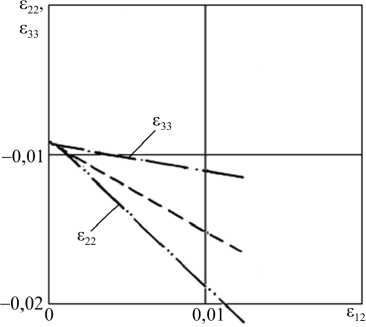
Рис. 7. Эффект расщепления деформаций в опытах И.М. Коровина по программе 2
Fig. 7. “Splitting of deformations” effect in I.M. Korovin’s experiments under load program 2
чувствительного к виду напряженного состояния. На этих же рисунках пунктирными кривыми приведены расчетные кривые ( £ 22 = £ 33 ) в случае нечувствительности материала к виду напряженного состояния.
В изложенном выше эксперименте не приводится данных об изменении кольцевой деформации £ 22 , что позволило бы сопоставить результаты расчета и эксперимента по компоненте Э 2 и выходу траектории деформаций из плоскости траектории напряжений. В экспериментальных исследованиях [3] приводятся необходимые для этого данные по кольцевой деформации. Эксперименты [3] проводились на трубчатых образцах из стали 30ХГСА при мягком нагружении ( ( Р, М )-опыты). Хотя чувствительность этого материала к виду напряженного состояния умеренная – отличие кривых растяжения (сжатия) и кручения составляет порядка 10 %, – выход траектории деформаций из плоскости траектории напряжений имеет место. Траектории напряжений показаны на рис. 9, 10. В программе 1 (см. рис. 9) образец растягивался осевой силой до сти = 500 МПа, а затем закручивался при постоянной осевой силе. В программе 2 (рис. 10) образец вначале закручивался до о 12 = 250 МПа, а далее растягивался осевой силой при постоянном моменте. Таким образом, в обеих программах реализовывались двузвенные траектории напряжений с ортогональным изломом. Экспериментальное подтверждение эффектов «расщепления» и выхода траектории деформаций из плоскости напряжений для ортогональных траекторий (рис. 9, 10) приводится на рис. 11, 12. Изменения составляющих тензора и вектора деформаций, полученные на основе расчетов, показаны соответственно сплошными и пунктирными кривыми. Результаты эксперимента [3] изображаются соответственно светлыми и темными кружками. Явно наблюдаются эффекты «расщепления» и выхода траектории деформаций из плоскости траектории напряжений. Соответствие между расчетом и экспериментом удовлетворительное – отличие не превышает 10 %.
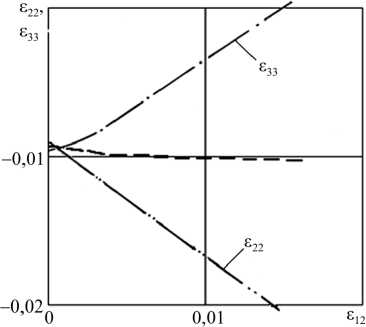
Рис. 8. Эффект расщепления деформаций в опытах И.М. Коровина по программе 3
Fig. 8. “Splitting of deformations” effect in I.M. Korovin’s experiments under load program 3
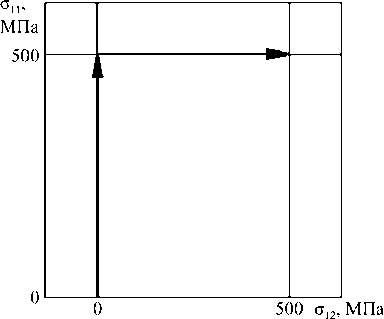
Рис. 9. Траектория напряжений в опытах
А.С. Вавакина и соавторов по программе 1
Fig. 9. Stresses trajectory in A.S. Vavakin and coauthors’ experiments under load program 1
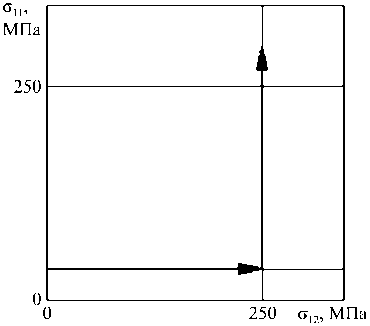
Рис. 10. Траектория напряжений в опытах
А.С. Вавакина и соавторов по программе 2
Fig. 10. Stresses trajectory in A.S. Vavakin and coauthors’ experiments under load program 2
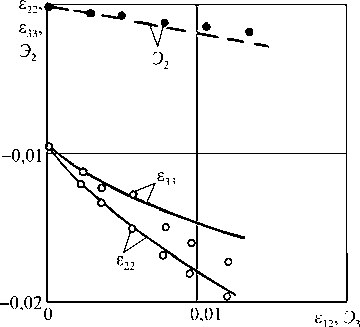
Рис. 11. Эффект расщепления деформаций и эффект Э 2
в опытах А.С. Вавакина и соавторов по программе 1
Fig. 11. “Splitting of deformations” effect and Э2 effect in A.S. Vavakin and coauthors’ experiments under load program 1
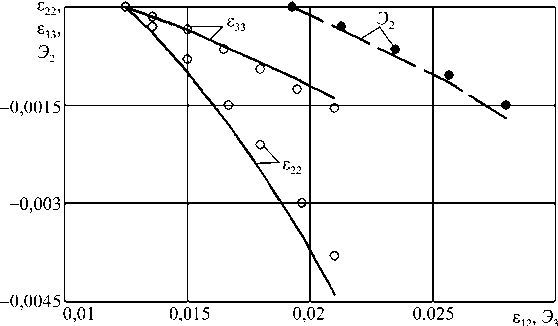
Рис. 12. Эффект расщепления деформаций и эффект Э 2
в опытах А.С. Вавакина и соавторов по программе 2
Fig. 12. “Splitting of deformations” effect and Э2 effect in A.S. Vavakin and coauthors’ experiments under load program 2
Заключение
Сопоставление расчетных и экспериментальных результатов показывает, что предложенный вариант теории упругопластического деформирования достоверно описывает поведение материалов, чувствительных к виду напряженного состояния.
Рассмотрен эффект «расщепления» деформаций, приводящий к тому, что лучевым траекториям дефор- маций (напряжений) могут отвечать нелучевые траектории напряжений (деформаций), а плоским траекториям – неплоские.
Список литературы Пластическое деформирование материалов, чувствительных к виду напряженного состояния
- Коровин И.М. Экспериментальное определение зависимости напряжение-деформация при сложном нагружении по траекториям с одной точкой излома//Инж. журн. МТТ. -1964. -№ 3. -С. 592-600.
- Ohashi Y. Effect of Complicated deformation history on inelastic deformation behavior of metals//Memoirs of Faculty of Engineering Nagoya University. -1982. -Vol. 34. -No. 1. -P. 1-76.
- Вавакин А.С., Мохель А.Н., Степанов Л.П. Исследование характера пластического деформирования стали 30ХГСА в точках резкого излома траектории нагружении (P -M-опыты)/Деп. ВИНИТИ № 2895-83. -М., 1983. -102 c.
- Ильюшин А.А. Пластичность. Основы общей математической теории. -М.: Изд-во АН СССР, 1963. -271 с.
- Кадашевич Ю.И., Новожилов В.В. Теория пластичности, учитывающая остаточные микронапряжения//ПММ. -1958. -Т. 22. -Вып. 1. -С. 78-89.
- Новожилов В.В. О пластическом разрыхлении//ПММ. -1965. -Т. 29. -Вып. 4. -С. 681-689.
- Кадашевич Ю.И. Теория пластичности, учитывающая эффект Баушингера и влияние среднего нормального напряжения на границу текучести//Тр. Ленигр. технол. ин-та целлюлозно-бум. пром-ти. -1965. -Вып. 18. -С. 234-235.
- Коротких Ю.Г. Описание процессов накопления повреждений материала при неизотермическом вязкопластическом деформировании//Проблемы прочности. -1985. -№ 1. -С. 18-23.
- Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. -М.: Физматлит, 2008. -424 с.
- Ломакин Е.В. Зависимость предельного состояния композитных и полимерных материалов от вида напряженного состояния//Механика композитных материалов. -1988. -№ 1. -С. 3-9.
- Ломакин Е.В., Федулов Б.Н. Пластическое деформирование полос из материала с зависящими от вида напряженного состояния свойствами//Вестн. СамГУ. Естественно-научная сер. -2007. -№ 4(54). -С. 263-279.
- Ломакин Е.В. Пластическое течение дилатирующей среды в условиях плоской деформации//Изв. РАН. МТТ. -2000. -№ 6. -С. 58-68.
- Lomakin E.V. Topical Problems in Solid Mechanics. Eds. N.K. Gupta, A.V. Manzhirov. -New Delhi: IIt Delhi. -2008. -P. 122-132.
- Ломакин Е.В., Федулов Б.Н. Теория пластичности и предельного равновесия тел, чувствительных к виду напряженного состояния//Вестн. Нижегород. ун-та им. Н.И. Лобачевского. -2011. -№ 4(4). -С. 1585-1587.
- Федулов Б.Н. Предельное пластическое состояние полосы с отверстием из дилатирующего материала//Вестн. МГУ. Сер. 1. Математика. Механика. -2007. -№ 6. -С. 40-44.
- Ломакин Е.В., Федулов Б.Н. Растяжение полосы, ослабленный вырезами с круговым основанием, в условиях плоской деформации из материала с зависящими от вида напряженного состояния свойствами//Механика твердого тела. -2013. -№ 4. -С. 80-87.
- Расчеты машиностроительных конструкций методом конечных элементов: справ./под общ. ред. В.И. Мяченкова. -М.: Машиностроение, 1989. -520 с.
- Бондарь В.С., Фролов А.Н. Математическое моделирование процессов неупругого поведения и накопления повреждений материала при сложном нагружении//Изв. АН СССР. МТТ. -1990. -№ 6. -C. 99-107.
- Бондарь В.С. Неупругое поведение и разрушение материалов и конструкций при сложном неизотермическом нагружении: дис. … д-ра физ.-мат. наук. -М.: Изд-во МАМИ, 1990. -314 с.
- Бондарь В.С. Неупругость. Варианты теории. -М.: Физматлит, 2004. -144 с.
- Бондарь В.С., Даншин В.В. Пластичность. Пропорциональные и непропорциональные нагружения. -М.: Физматлит, 2008. -174 с.
- Bondar V.S. Inelasticity. Variants of the theory. -New York: Begell House, 2013. -194 p.
- Aravas N. On the Numerical Integration of a Class of Pressure-Dependent Plasticity Models//Int. J. Numer. Methods in Enging. -1987. -Vol. 24. -No. 7. -P. 1395-1416.
- Bardet J. Lode dependences for isotropic pressure-sensitive elastoplastic materials//Journal of Applied Mechanics. -Transactions ASME. -1990. -Vol. 57 (3). -P. 498-506.
- Barlat F., Lege D.J., Brem J.C. A six-component yield function for anisotropic materials//International Journal of Plasticity. -1991. -Vol. 7 (7). -P. 693-712.
- Yielding description for solution strengthened aluminum alloys/F. Barlat, R.C. Becker, Y. Hayashida, Y. Maeda, M. Yanagawa, K. Chung, J.C. Brem, D.J. Lege, K. Matsui, S.J. Murtha, S. Hattori//International Journal of Plasticity. -1997. -Vol. 13 (4). -P. 385-401.
- Menetrey P., Willam K. Triaxial failure criterion for concrete and its generalization//ACI Structural Journal. -1995. -Vol. 92. -P. 311-318.
- Bigoni D., Piccolroza A. A new yield function for geomaterials. Constitutive Modeling and Analysis of Boundary Value Problems in Geotechnical Engineering. Ed. C. Viggiani. -Napoli, 2003. -P. 266-281.
- Linear transformation-based anisotropic yield functions/F. Barlat, H. Aretz, J. Yoon, M. Karabin, J. Brem, R. Dick//International Journal of Plasticity. -2005. -Vol. 21(5). -P. 1009-1039.
- Fossum A., Brannon R. On a viscoplastic model for rocks with mechanism-dependent characteristic times//Acta Geotechnica. -2006. -Vol. 1. -P. 89-106.
- Bai Y., Wierzbicki T. A new model of metal plasticity and fracture with pressure and Lode dependence//Int. J. Plasticity. -2008. -Vol. 24. -P. 1071-1096.
- Мовчан А.А. Феноменологическое описание дислокационного механизма образования дефектов при пластическом деформировании//Проблемы прочности. -1987. -№ 1. -С. 147-155.
- Зубчанинов В.Г. Механика сплошных деформируемых сред. -Тверь: Изд-во ТГТУ, 2000. -703 с.


