Пластическое течение и реоморфическая дифференциация вещества в мантийных ультрамафитах

В настоящее время считается общепринятым, что верхняя мантия Земли имеет ультраосновной состав [30 и др.], вещество ее находится в вязкопластическом состоянии и поэтому в ней могут возникать адвективные [10, 52] и/или конвективные течения [28, 29, 44, 46 и др.], построены многочисленные модели конвек-тирующей мантии (например, [15, 45 и др.]). Вместе с тем одно из следствий до- пущения о возможности возникновения вязких мантийных потоков остается обычно за рамками рассмотрения. Оно состоит в том, что течения возникают в среде, не являющейся истинным флюидом, а обладающей полифазным минеральным составом. Такие течения неизбежно должны вести к перестройке внутренней структуры и вещественным преобразованиям. Направленность структурных и вещественных изменений будет зависеть от конфигурации силовых полей, иниции-

рующих потоки, и от физических свойств частиц, слагающих данную геологическую среду.

Одним из источников информации об особенностях состава и строения верхней мантии геологического прошлого являются ультрамафиты, обнажающиеся в составе офиолитовых ассоциаций складчатых поясов. В настоящей статье проведен анализ главных особенностей строения офиолитовых ультрамафитов, сформулированы основные проблемы существующих генетических концепций, а также предложена оригинальная физическая модель реоморфической дифференциации вещества верхней мантии, позволяющая их разрешить.

Состав и строение ультрамафитов складчатых поясов

Прямую информацию о составе и строении верхней мантии Земли можно получить из трех основных источников: 1) керна глубоководного бурения и материала драгировок с дна Мирового океана, 2) ультраосновных ксенолитов из внутри-плитных базальтов континентов и океанических плит, 3) ультрамафитовых массивов, обнажающихся в составе офиолитовых комплексов.

Многочисленные исследования представителей трех названных типов геологических объектов показали, что, несмотря на некоторые второстепенные особенности, их объединяет главное: ультраос-новной (существенно перидотитовый) состав и постоянное присутствие высокотемпературных пластических деформаций главных породообразующих минералов [30, 60 и др.], на которые затем накладываются вторичные низкотемпературные преобразования пород (в основном серпентинизация). В настоящем исследовании мы ограничимся рассмотрением только высокотемпературной (мантийной) истории ультрамафитов и не будем учитывать наложенные низкотемпературные (коровые) деформации. Учитывая, что наиболее представительный материал о составе и структуре верхней мантии дают офиолиты, в дальнейшем речь пойдет именно о них.

Первичные породы массивов являются ультраосновными тектонитами, претерпевшими высокотемпературное пластическое течение, и представляют собой тугоплавкий остаток (рестит), испытавший частичное плавление и экстракцию из него легкоплавкой базальтовой составляющей. Последняя часто присутствует либо во внутренних частях ультрамафитового разреза в виде даек габброидов, либо в краевых частях массивов формирует крупные дифференцированные тела пи-роксенит-габбрового состава. Наиболее интересны и дискуссионны особенности внутреннего строения реститового комплекса офиолитовых ультрамафитов. Выделим главные черты их строения:

• 1)    сравнительно однообразный минеральный состав рассматриваемых комплексов, которые на 65-80% состоят из магнезиального оливина (Fa 6-12 ), помимо которого в породах присутствуют в заметных количествах лишь энстатит, диопсид и хромшпинелид, спорадически встречаются плагиоклаз и гранат [16, 21 и др.];

• 2)    широкое распространение первичной полосчатости, обусловленной различными количественными соотношениями в «слоях» оливина, пироксенов и хромшпи-нелида, сочетание полосчатости с минеральной уплощенностью и линейностью [35, 37, 71 и др.];

• 3)    присутствие среди перидотитов (лерцолитов и гарцбургитов) дунитовых тел различного размера и морфологии, с дунитовыми телами часто связаны тела хромититов, также обладающие различными размерами, морфологией и степенью концентрации оруденения [27];

• 4)    обычно от перидотитов к дунитам происходит закономерное изменение морфологии и состава хромшпинелидов: ксеноморфные и глиноземистые в лерцолитах постепенно сменяются идиоморфными и высокохромистыми в дунитах и ассоциирующих с ними хромититах [17, 36, 40 и др.];

• 5)    хромититы всегда вмещаются дунитами, но их объемные соотношения в различных случаях могут значительно варьировать [17, 23, 27, 59, 76 и др.];

• 6)    повсеместное распространение в породах следов высокотемпературного пластического течения, отраженного морфологически: в образовании полос скольжения и субзерен в оливине и энстатите, механическом двойниковании пироксенов, изгибе плоскостных элементов строения (ламеллей диопсида, трещин спайности в энстатите); петроструктурно: в образовании предпочтительных оптических ориентировок зерен оливина и пироксенов, идентичных таковым, полученным экспериментально при деформации ультрама-фитов при высоком давлении и температуре [54, 57, 72 и др.].

Помимо указанных выше главных закономерностей строения ультрамафито-вых комплексов, особо следует отметить характер взаимоотношений между шпинелевыми перидотитами, составляющими основу разреза реститов, и дунитами, обычно имеющими подчиненное значение. В состав шпинелевых перидотитов помимо оливина (60-80% по объему) входит заметное количество пироксенов (ортопироксен 15-25%, клинопироксен до 15%), тогда как дуниты являются практически мономинеральными оливиновыми породами. Анализ обширного фактического материала по офиолитовым комплексам мира показывает, что во всех случаях дуниты являются «более поздними», «эпигенетическими» образованиями по отношению к перидотитам [23, 31, 39, 54, 66 и др.]. Это выражается в пересечении дуни-товыми жилами полосчатых гарцбургитов, формировании сетчатого дунит-гарцбургитового комплекса, дунитовых штокверков, будинаже гарцбургитов, включенных в дунитовую матрицу [17]. По мнению авторов настоящей статьи, наблюдаемые явления объясняются не столько «полихронностью» происхождения пород, сколько различной их мобильностью в условиях мантийного пластического потока [35, 36].

Аналогичные взаимоотношения можно наблюдать на микроскопическом уровне между ортопироксеном (энстатитом) и оливином. Одним из первых на меньшую вязкость оливина по сравнению с энстатитом в процессе деформации мантийных ультрабазитов указал А.Николя с соавторами при описании альпийских массивов [71]. В цитируемой работе показано, что при одних и тех же условиях деформирования в зернах оливина происходит трансляционное скольжение в направлении смещения, а в зернах ортопироксена наблюдается разрыв. Подобные соотношения между породообразующими минералами ультрамафитов часто наблюдаются и на массивах Южного Урала [32, 36].

Многочисленные экспериментальные исследования также показали, что в широком диапазоне Р-Т- ε условий вязкость агрегатов энстатита примерно на 25% выше, чем форстерита [57, 61], для оливина характерно явление гидролитического ослабления [64], а также более высокая скорость рекристаллизации отжига по сравнению с пироксенами [57].

Таким образом, рассмотренные выше главные особенности строения и состава офиолитовых ультрамафитов позволяют предположить, что основным механизмом их становления было твердофазное (рео-морфическое) течение в условиях верхней мантии. Прежде чем перейти к изложению физической модели реоморфической дифференциации мантийного вещества, рассмотрим существующие генетические представления и обозначим основные проблемы, связанные с предлагаемыми в них механизмами петрогенезиса.

Основные генетические концепции и их проблемы

Происхождение ультраосновных пород офиолитовых комплексов и связанных с ними месторождений хрома на протяжении долгих лет является предметом оживленной дискуссии. В первой половине XX столетия господствующей гипотезой образования хромититов являлась магматиче- ская, в рамках которой они рассматривались как продукты дифференциации ульт-раосновной магмы (дунитовой или перидотитовой) [6, 17, 20, 22, 26, 42, 43 и др.]. Развитие метасоматической гипотезы [4, 23, 31 и др.], рассматривающей дунит-гарцбургитовые комплексы с хромовым оруденением как продукт метасоматических преобразований перидотитового (эн-статититового) субстрата, было вызвано главным образом невозможностью объяснить магматической дифференциацией факт «эпигенетичности» дунитов и хро-мититов (более тугоплавких) по отношению к окружающим гарцбургитам.

К разновидностям метасоматической гипотезы можно отнести и реакционномагматическую модель образования ульт-рамафитов и хромовых руд в офиолитах, которая в последние годы имеет колоссальное влияние на специалистов, изучающих ультрамафиты во всем мире [5, 38, 65, 66, 78 и др.]. Суть гипотезы сводится к следующему. Гарцбургиты и дуниты офиолитовых комплексов являются не простыми тугоплавкими остатками от частичного плавления пиролита, а представляют собой результат реакции рестита с проникающими сквозь него расплавами, генерированными на большей глубине. Расплавы «расторгают» пироксены и «кристаллизуют» дополнительный оливин, что в предельном случае ведет к формированию дунитов. В некоторых интерпретациях дуниты считаются изолированными «каналами», по которым базальтовые расплавы транспортируются к поверхности [67]. При этом образование хромититов связывается исключительно с транспортировкой сквозь перидотиты бонинитовых расплавов, реакцией бонинитов с перидотитами, расторжением пироксенов, осаждением оливина и высокохро-мистого шпинелида [78 и др.].

Против реакционной (метасоматической) интерпретации петрогенезиса в верхней мантии можно выдвинуть ряд аргументов.

Аргумент 1. В метасоматических гипотезах, как правило, отсутствует описа- ние механизмов растворения – переноса – осаждения мантийного материала, в первую очередь весьма инертного хрома. За исключением реакционно-магматической все они апеллируют к гипотетическим агентам массопереноса, не указывая их конкретного состава.

Аргумент 2. В гарцбургитах, дунитах и хромититах отсутствуют вещественные доказательства образования их при активном участии флюидной фазы. Высокотемпературные «флюидные» минералы (амфиболы, флогопит) здесь обычно отсутствуют.

Аргумент 3. Отсутствуют реакционные взаимоотношения между породообразующими минералами ультрамафитов, например, между оливином и ортопироксеном. При метасоматическом образовании оливина на месте пироксенов в процессе замещения под воздействием флюидов такие соотношения должны наблюдаться повсеместно (везде, где сохранился энстатит), иначе следует признать, что «оливи-низация» – мгновенный процесс, а это противоречит здравому смыслу.

Аргумент 4. Для метасоматических гипотез мантийные ультрабазиты представляют собой статичную субстанцию, сквозь которую проникают расплавы или флюиды и преобразуют ее химическим путем. Максимально, что «дозволяется» кристаллическому каркасу, так это испытывать незначительную деформацию, в результате которой из них удаляется частичный расплав. В то же время без обсуждения предполагается, что все процессы плавления, просачивания и реакции расплава с остаточными минералами происходят внутри поднимающегося мантийного вещества (mantle diapir, upwelling mantle). Механизм этого подъема и его влияние на структуру и вещественный состав мантийного субстрата обычно не рассматриваются.

Аргумент 5. В рамках метасоматических гипотез, в том числе реакционномагматической, нельзя объяснить резкие контакты дунитов и гарцбургитов, а также увеличение содержания ортопироксена в приконтактовых частях гарцбургитов, что очень часто наблюдается в офиолитовых массивах [35].

Аргумент 6. Если дунит – канал, то в нем должно быть достаточно много расплава вплоть до момента «замерзания» системы. Если в момент ее «замерзания» в канале много расплава, то это уже не дунит, т. к. при кристаллизации расплава должно происходить образование базаль-тоидной ассоциации (пироксены, плагиоклаз) и порода по составу будет уже соответствовать лерцолиту. Если же в «канале» при его «замерзании» расплав отсутствует, то может ли он считаться каналом, где протекал расплав? В реальных офиолитах, которые послужили полигоном для разработки реакционномагматических моделей, наблюдаются именно дуниты.

Аргумент 7. В рамках реакционномагматической гипотезы отсутствует механизм образования хромититов как геологических тел. Даже если принять точку зрения, что хромит кристаллизуется в дуните при «расторжении» пироксенов, остается непонятным, какие факторы заставляют его формировать отдельные тела с различающейся концентрацией – от ред-ковкрапленных до массивных руд.

Таким образом, традиционные гипотезы образования ультрамафитов складчатых поясов – магматическая и метасоматическая (включая реакционномагматическую) – сталкиваются с серьезными проблемами при объяснении генезиса хромовых руд в офиолитах. Альтернативой для них является признание ведущим механизмом дифференциации вещества реоморфическое (твердофазное) течение ультрамафитов. Со времени первых исследований пластического течения ультрамафитов, инициированных Григгсом, достигнуты большие успехи как в понимании механизмов пластической деформации главных породообразующих минералов верхней мантии, так и процессов формирования офиолитовых комплексов [9, 37, 51, 54, 56, 57,58, 61, 71, 72, 63, 64, 68 и др.]. Вместе с тем, признавая важную роль пластических деформаций в образовании структуры ультрамафитовых тел, исследователи в большинстве случаев обходят стороной вопрос о связи тектонического течения и дифференциации вещества верхней мантии, и лишь в отдельных работах делается вывод о ведущей роли реоморфизма в процессе мантийного петро- и рудогенеза [3, 11, 34, 35, 36, 50, 54]. В следующем разделе мы представляем физическую модель реоморфической дифференциации мантийного материала, в основе которой лежит термодинамический подход.

Физическая модель реоморфической дифференциации

Рассматриваемые нами в этом разделе геологические структуры не являются изолированными системами. Они обмениваются с внешней средой энергией в виде упругих (сейсмических) волн, теплопере-носа, либо создают вокруг себя поля упругих напряжений, имеют сложный неоднородный химический и фазовый состав и т.п. Поэтому далее для описания подобных систем используется термодинамический подход.

Как известно, в геологических объектах широким распространением пользуется вертикальная стратификация, возникающая в условиях гравитационного поля и образующаяся при осаждении более плотных фаз (кристаллов и обломочных зерен) в менее плотной жидкости (расплаве или воде). Напротив, главной особенностью рассматриваемых нами ультрама-фитовых комплексов является неоднородность распределения компонентов по горизонтальному сечению. Поэтому необходимо выделить внешние факторы, способные создать горизонтальные градиенты распределения компонентов. Кроме гравитационного поля существует множество иных факторов, вызывающих изменения в составе и распределении компонентов в пространстве. К ним можно отнести неоднородность температуры и/или концентрации в слоях, граничащих с рас- сматриваемой системой, внешние источники акустического (вибрационного и сейсмического) воздействия, гидростатические поля (тектонические напряжения), вязкопластические потоки. С каждым из этих факторов можно связать возникновение соответствующих обобщенных сил, проявляющихся в виде разнообразных эффектов (Бенара, Киркендалла, Френкеля), сопровождающихся массопереносом и перераспределением компонентов в горизонтальном направлении. Ограничим рассмотрение только гидродинамическим полем, полагая, что вибрации и температурные градиенты отсутствуют или несущественны.

Гидродинамические поля возникают в породах восходящего мантийного диапира. Эти поля возникают при вязкопластических течениях в твердофазных системах. Сами течения могут быть вызваны разными причинами: компрессией– декомпрессией в окружающих породах, разностью температуры в окружающих систему слоях (термоконвекция), конвекционные течения могут возникать и под действием гравитационного поля [2].

Скорости массопереноса и перераспределения компонентов в условиях вязкопластических потоков могут существенно превышать скорость диффузионных процессов. Поэтому существование вязкопластических течений любого происхождения можно рассматривать в числе факторов, участвующих в формировании структуры верхней мантии.

Экспериментальные наблюдения потоков в двухфазных системах разного типа показали, что частицы в них могут смещаться перпендикулярно оси потока в различных направлениях. Экспериментально установлено, что в вертикальном нисходящем или горизонтальном потоке частицы, имеющие плотность более высокую, чем плотность среды, смещаются к стенке, а частицы с меньшей плотностью – к оси потока. Концентрация дисперсной фазы может быть неоднородной и несимметричной, жидкие частицы могут образовывать пленки на стенках, пузырьки всплывают преимущественно по центральной области вертикальных потоков, крупные частицы могут двигаться, сталкиваясь со стенками, ограничивающими поток. Частицы с нулевой плавучестью двигаются, концентрируясь на удалении и от стенок, и от оси потока, либо осциллируют внутри потока. На движение частиц оказывает влияние множество факторов, в частности, геометрия, скорость, плотность частиц и среды [7, 47].

Многочисленные обзорные работы, экспериментальные и численные исследования последних лет свидетельствуют, что проблема теоретического описания миграции частиц в потоках самого разного типа остаётся актуальной и в настоящее время [8, 13, 69, 73]. Классическое описание основано на аппарате гидродинамики [18, 25, 47], существуют работы, в которых привлекаются методы и понятия статистической физики и термодинамики [12, 13, 14, 41, 48].

Рассмотрим процессы массопереноса в стационарном гидродинамическом поле. Поместим тело массой m b в среду с плотностью ρ , которая движется равномерно и прямолинейно. При этом сечение потока, средняя скорость и эпюра скоростей остаются постоянными по всей длине потока. Простейшими примерами таких потоков являются течение Куэтта – ламинарное течение вязкой жидкости между двумя параллельными стенками/плитами, одна из которых двигается относительно другой, и течение Пуазейля – ламинарное течение вязкой жидкости через каналы в виде прямого кругового цилиндра или слоя между параллельными стенками/плитами под действием перепада давления.

Свяжем систему координат с неподвижной границей потока так, что ось x совпадет с направлением потока, а ось z будет нормальна границам.

Рассмотрим случай, при котором скорость движения центра тела, находящегося на расстоянии r от неподвижной стенки, равна скорости течения v(r) среды на том же уровне. Пусть за время наблюдения тело не успевает смещаться поперёк потока и не вращается под действием обтекающих его потоков.

Система является стационарной, т. к. полная и внутренняя энергия, импульс, количество вещества, состав, масса, объемы жидкой и твёрдой фаз не зависят от времени. Полная энергия системы "тело + среда" имеет вид

F ( r ) = —— W ( r ) стремится изменить по- dr

W = MVL + U , 2

где масса системы M = ^ m i складывается из масс m i , составляющих систему частей. V 0 – скорость движения центра инерции системы в выбранной системе координат, т.е. относительно неподвижной стенки. Внутренняя энергия U включает кинетическую энергию относительного (по отношению к центру инерции системы) движения всех частей системы и потенциальную энергию их взаимодействия [19].

Опишем состояние системы в зависимости от положения тела в потоке. Потенциальную энергию взаимодействия тела со средой примем равной нулю. Тогда внутренняя энергия системы включает только кинетическую энергию движения среды и тела относительно центра инерции системы, движущегося со скоростью V 0 . Пренебрегая локальными потоками среды в окрестности тела, связанными с тем, что один край двигается быстрее потока, а другой медленнее, представим полную энергию системы как

H L r + L2,

W ( r ) = Ap j v ( z ) dz +— j ( pv ⁽ r ) — pv ^{2 (} z )) dz , ⁽²⁾ 00 ² r-Lf' 0

здесь А – параметр, по смыслу соответствующий площади горизонтального сечения системы. Первый интеграл соответствует энергии среды при отсутствии тела. Второе слагаемое равно энергии тела и учитывает энергию среды, которую заменило тело. Предполагается, что тело с плотностью ρ b имеет форму куба со стороной L , основание куба ориентировано параллельно стенкам потока.

Энергия системы (2) зависит от положения тела r. Обобщенная сила

ложение тела и определяет направление самопроизвольного перемещения компонентов системы (тела и среды), при которых полная энергия системы понижается.

В простейшем случае плоского сдвигового течения Куэтта v ( z ) = az действует

сила

F (r)

a ² rm ₀

(

—

k

"

Po J

dv                              3

где a = — - скорость сдвига, m_b = L p_b , m 0 = L ³ ρ 0 – масса тела и масса среды, вы-

тесненной телом, ρ b , ρ 0 – плотность тела и среды соответственно. При нулевой плавучести тела ( ρ b = ρ 0 ) выталкивающая сила отсутствует. Для "легких" тел ( ρ b <  ρ 0 )

сила направлена в сторону увеличения скорости потока. Для "тяжелых" ( ρ b >  ρ 0 ) тел сила направлена в сторону уменьшения скорости потока, к его неподвижной границе.

Существенное отличие силы (3) от силы Архимеда состоит в том, что F ( r ) зависит от положения тела относительно границ системы. Для течения Куэтта это кажется странным, ведь при любом r разность скоростей в окрестности тела одинакова. Однако, вспоминая, что сила дей-

ствует и на тело, и на среду, можно представить это следующим образом: слои, расположенные между неподвижной стенкой и телом, выполняют роль рычага. Как и сила Архимеда, это пример обобщенных или "термодинамических сил", действующих на систему в целом , а не на отдельные составляющие систему тела. Обобщенной координатой является координата центра тяжести тела r . То, что формально сила привязана к положению тела, создаёт иллюзию, что сила действует именно на тело.

Рассмотрим более сложный случай, когда тело движется относительно среды со скоростью v b = v ( r ) + Δ v. Гидродинамика не предлагает простого и однозначного уравнения, описывающего выталкивающую силу в этом случае, поэтому вос-

пользуемся уравнением (2), принимаю-

щим вид

J ч H          r + L2 P ( v ( r j +^ v j ² — P v ⁽ z ⁾

Wr )= Apfv ( z ) dz + L ²j b^      ⁾— dz +A W .⁽⁴⁾

00                  r2                 ²

При больших отклонениях скорости тела от скорости среды пренебрежение вкладом локальных потоков, возникающих в окрестности тела Δ W loc , становится некорректным. Чем сильнее скорость тела отличается от скорости среды, тем больше вклад Δ W loc . Выталкивающая сила, действующая на движущееся в потоке Куэтта

силы) [70]. Есть другие выражения, например, F M = 1.96 ( b 1 Re _p + b ₂ ) p ₀ d ³A va [24] или F Y = 0.052 p ₀ d ³A va , описываю-

тело, имеет вид

F ( r , A v ) = a ² m r 1

—-

I  p0J

^— am_b ^{A v —} d W . (5) dr

щее силу в условиях конкретного эксперимента [77]. В (6), как во всех приведённых уравнениях, сила пропорциональна массе жидкости, вытесненной телом, относительной скорости тела, скорости сдвига, а направление силы может быть разным в зависимости от плотности тел.

Рассмотрим некоторые частные случаи. Для «легких» тел ρ 0 >>  ρ b при малой скорости относительного движения тел |A v | <<  d|a | <  r |a | сила (6) приближенно

В геологических системах при вязко-

пластическом течении относительная скорость движения тел Δ v в твёрдой среде не

равна

F ( r , A v )

far+-] Иv Po J

m ₀ A va .

велика, и последним слагаемым мы пренебрежём. Сгруппируем оставшиеся слагаемые следующим образом:

Она направлена в сторону увеличения r и

F (r, Av ) =

ar ! — л + ^P

A v I Po J Po

p₀ L ³A va

стремится сместить тела, опережающие поток Δ v > 0, в направлении увеличения скорости потока. Если же тело отстаёт от потока Δ v < 0 (например, пузыри в «падающем» потоке), то сила меняет знак при

и сравним эту силу с ранее описанными силами [25]. Выражение (6) не зависит от предыстории, поэтому не имеет отношения к силе Бассэ-Бусинеска, возникающей при ускоренном движении тел. В рассматриваемой модели тело не вращается, поэтому силы Магнуса и Саффмена, зависящие от угловой скорости, отсутствуют. Сила (6) никаким образом не зависит от вязкости среды и не является силой тре- ния.

Описывая движение не вращающегося тела в сдвиговом потоке, часто применяют другую силу Саффмана [53, 74]. В используемых обозначениях она имеет вид

—

F s =

0.5 ^µ

CS T

V L J m 0 A va 05

. Эта сила полу-

чена для неинерционной системы отсчета (привязана к движущемуся телу), что осложняет сопоставление с вариантом (6). Коэффициент C s сложным образом зависит от скорости потока и свойств среды [55]. При изменении условий течения C s может менять знак (направление действия

= P b ^{A v}

ρ 0 a

и направлена в сторону роста скорости потока при r > r0 и в сторону неподвижной стенки при r < r0.

Для тел большой плотности ρ 0 <<  ρ b выражение (6) имеет вид

F ( r , A v ) » ^f 1 —   ] — p ₀ L" A va .

I Av J Po

Сила стремится сместить тяжёлые тела, опережающие поток Δ v > 0 (например, тяжелые тела в восходящем потоке), на

A v уровень r = — .

Различные варианты поведения тел наглядно иллюстрирует зависимость энергии системы от положения и скорости тел в потоке Куэтта (рис. 1). Система, стремясь понизить свою энергию, переносит тела в сторону минимумов энергии.

Для плоского течения Пуазейля v ( z ) = b ( zH - z ²), 0 <  z <  H , где b - параметр, определяющий вид эпюры скоростей, H – ширина потока между неподвижными стенками, пропуская

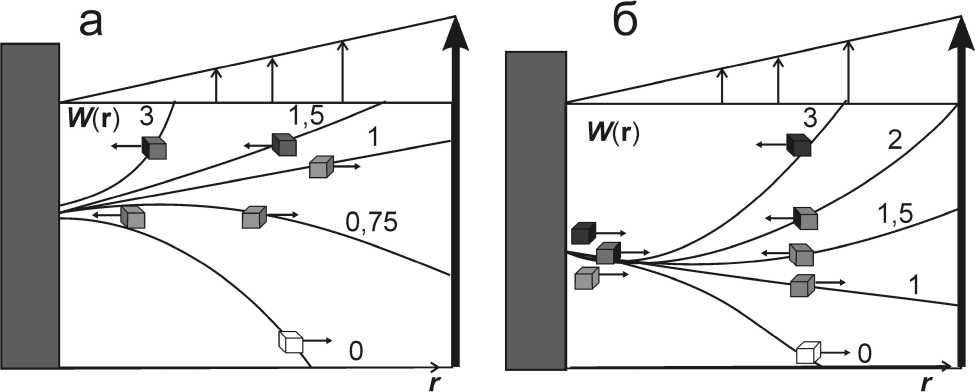
Рис. 1. Зависимость энергии системы от положения тел r в потоке Куэтта для тел, опережающих поток (а) и отстающих от потока (б). Рядом с кривыми указано отношение плотности тел к плотности среды ρ b /ρ 0 . Относительная плотность пузырей принята равной 0, тел с нулевой плавучестью – 1. Стрелками указано направление силы, действующей на тела разной плотности

громоздкую аналитическую запись полной энергии системы, получим

F ( r, F= m o b-

^ ](У H + H^ ^{[ r} - ^

Сила формально разбивается на составляющие, одна из которых зависит от плотности компонентов системы, обращаясь в 0 для тел с нулевой плавучестью (ρb = ρ0), другая от плотности не зависит и действует даже на тела с нулевой плавучестью. В потоке Пуазейля выталкивающая сила зависит и от положения тела относи- тельно стенки r, и от размеров тела L. Вводя безразмерные координаты, можно получить выражение

F ( q ) = A

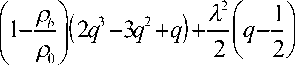
, (9)

где q = h / H , 0 <  q <  1 для пространственной координаты и Л = L / H, 0 <  Л < 1 для размеров тела, A = р₀ L H ³ b ² - коэффициент, учитывающий геометрические характеристики.

Выталкивающая сила (9) антисимметрична относительно середины потока. В центре потока направление силы меняется на противоположное. Полином (2q3 – 3q2 + q) имеет экстремумы в точках q = ‘/г ± 3/66 (0.211, 0.789), симметрич- ных относительно середины потока. Они соответствуют слоям, где вклад первого слагаемого в выталкивающую силу максимален.

Вклад второго слагаемого пропорционален размерам тела и линейно растёт при удалении от центра потока. Независимо от плотности тела эта составляющая выталкивающей силы направлена к стенкам. Для очень мелких частиц ( Л ^ 0) вторым слагаемым можно пренебречь.

В центре потока ( q = 0.5) выталкивающая сила равна нулю. Это соответствует положению равновесия, которое в зависимости от размеров и плотности тел может оказаться устойчивым или неустойчивым (рис. 2).

Для тел большой плотности ( ρ b >  ρ 0 ) сила всюду направлена к ближайшей стенке (рис. 2), но максимальное по величине значение она имеет на некотором удалении от нее. На тела с нулевой плавучестью ( ρ b = ρ 0 ) действует сила F ( q ) = A ^-^ q -^ , которая тоже всюду направлена от центра потока к стенкам.

Для тел любой плотности в окрестности неподвижных стенок ( q = 0 и q = 1) выталкивающая сила не равна нулю, прижимая тела к неподвижной стенке,

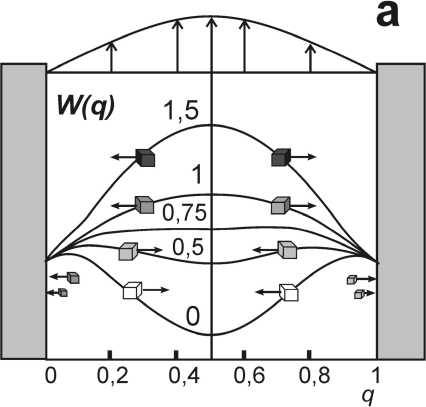
Рис. 2 . Зависимость энергии системы от положения тела r в потоке Пуазейля: а - скорости тела и потока равны; б - тело отстаёт от потока. Цифрами указано отношение плотности тела к плотности среды ρ b /ρ 0 . Относительная плотность каверн или пузырей принята равной 0, тел с нулевой плавучестью – 1. Стрелками показано направление силы, действующей на тела разной плотности

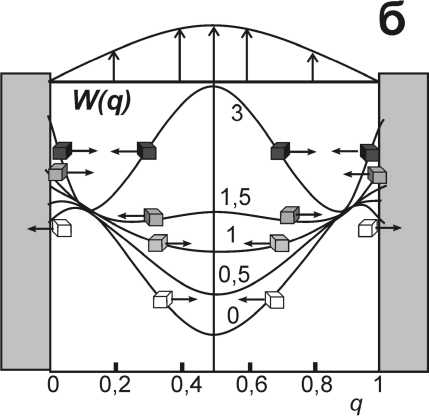
она становится «прижимающей» силой.

Для тел, плотность которых меньше плотности среды, в центральной части потока сила направлена к центру, а на периферии – к стенкам (рис. 2). Положения около q ~ ^ ± 3з 6 6 ( q < 0.211 и q ≥ 0.789), где выталкивающая сила обращается в 0 и меняет направление, зависят от размера и плотности тела. Они соответствуют максимумам энергии (рис. 3) и являются неустойчивым равновесием.

Согласно экспериментальным наблюдениям, в двухфазных потоках частицы могут концентрироваться в положении q « 0.1 v 0.2 и q « 0.8 ^ 0.9, причём центральная часть потока содержит сравнительно мало частиц [47]. Используя термодинамический подход, можно обнаружить, что эта ситуация может возникнуть в потоках Пуазейля, когда скорость "тяжёлых" тел меньше скорости потока Δ v < 0.

Скопления легких компонентов у стенок (см. рис. 2,б) могут образовать слои, двигающиеся в обратном основному потоку направлении. В потоках возможны и другие слоистые структуры (рис. 1–2).

Рассмотренная выше модель, в которой единственная частица двигается прямолинейно и равномерно вместе с потоком среды, практически не выходит за рамки ме- ханики. При описании движения множества тел (дисперсной фазы) в потоке следует использовать в качестве термодинамического потенциала не внутреннюю энергию системы U, а свободную энергию Гиббса G =U + PV – TS или Гельмгольца G =U – TS, где Р – давление, V – объём, T – температура, S – энтропия. Энтропийный вклад позволяет рассмотреть пространственное распределение тел в потоке. При этом появляется другая обобщенная сила, связанная с разностью концентрации дисперсной фазы.

Пусть рассматриваемая система имеет возможность изменять свою энергию, суммарное количество и состав компонентов не меняются во времени (закрытая термодинамическая система). Самопроизвольные процессы в механике происходят в направлении уменьшения энергии системы. Обмен энергией с окружающими геологическими слоями может происходить как на стенках, так и вдоль потока. Выделяющаяся при этом энергия может рассеиваться в виде гидродинамических, акустических или тепловых возмущений, излучаемых системой. В реальных условиях подобные взаимодействия с окружающей средой могут сопровождаться также изменением эпюр скоростей потока, распределения гидростатического давления, рождением вихревых движений среды в окрестности переносимых потоком тел, перемещениями и поворотами самих тел.

В термодинамике самопроизвольные процессы происходят в направлении перехода в равновесное состояние. Критериями равновесного состояния являются экстремумы термодинамического потенциала (минимум свободной энергии или максимум энтропии системы и др.). Во внешнем поле одним из критериев термодинамического равновесия является условие инвариантности суммы химического и механического потенциала. Следуя работам [1, 49], назовём эту сумму механохимиче-ским потенциалом.

Концентрация дисперсных частиц в системе n(q) определяется их индивидуальными свойствами (масса, плотность, модуль упругости) и геометрической конфигурацией поля (однородное, центрально-симметричное, распределенное и др.). Если система содержит несколько компонентов, условием термодинамического равновесия является инвариантность ме-ханохимического потенциала для каждого из компонентов системы:

Ц = ц ( q ) + u ( q ) + p ( q ) V ( q ) ^{+ 0 ln} ( n ( q ) ) = cos, (1 ¹ 0) здесь q – координаты, p ( q ) – гидростатическое давление, V i ( q ) – удельный (на моль или на одну частицу) объём компонента, для несжимаемых компонентов это константа, n l ( q ) – мольная доля компонента, µ_i^o – стандартный химический потенциал компонента. Слагаемое θ ln( n i ) – это энтропийный вклад (энтропия смешения).

Для систем с вязкопластическим тече- нием в однородном гравитационном поле условие инвариантности механохимиче- ского потенциала принимает вид v x, y, z) П,= Ц + pV gz + ( ,^ )

I 2 J

+

, (11)

+ p ( x, y, z ) V i + 0 In ( n i ( x, y, z ) ) = const здесь g – ускорение свободного падения, ρ , V – плотность и удельный (на моль или на одну частицу) объём компонентов, n l ( h )

– доля частиц типа , p ( h ) – гидростатическое давление, v ( x,y,z ) – скорость потока, координата z направлена вверх. Для однокомпонентной несжимаемой жидкости n i = 1 это выражение становится аналогом уравнения Бернулли.

Выражения типа (11) описывают гип- сометрические распределения Для объемного намическом и (11) следует

n ( q ) = C exp -

или пространственные дисперсных компонентов. распределения в гидроди-гравитационном поле из

^M ‘ [ gz ⁺ v ( f^

I ² J

θ

⁺ p ( q ) V

Для слоя, расположенного на фиксированной высоте z = const с прямолинейным горизонтальным ламинарным потоком вдоль оси y, распределение упрощается до

V ( x ) 2

M i ^2- + p ( x V

n ( x ) = Ce      ⁰     .     (12)

Различия в концентрации частиц определены эпюрой скорости v(x) и свойствами компонентов. Для крупнодисперсных систем это выражение имеет смысл ис- пользовать только в окрестности минимумов внутренней энергии U (рис. 1–2) либо в виде отношения концентрации частиц разного типа. Например, для смеси частиц А и В в дисперсионной среде плотностью

ρ0 на основе уравнения (12) получим nA (q) nB (q)

= c ab ^e xp

— ( pAVA - pBVB +( VA - VB ) po ) -q здесь константа САВ определяется исходным составом системы, VА, VВ – объём, а ρА, ρВ – плотность частиц типа А и В соответственно. Это уравнение показывает тенденцию изменения состава дисперсной системы в разных частях потока.

ПРи ( Pa + Po) Va <( Pb + Po) Vb , или — < Pb + Po , (13) VB Pa + Po доля частиц А будет возрастать там, где скорость потока больше. Здесь возможны варианты:

• -    частицы одного размера

( p _A + р о )/( р в + P o ) > 1, что эквивалентно

P A >  P B, — менее плотные там, где скорость выше;

• -    частицы равной плотности V A / V B < 1 – мелкие частицы преобладают там, где скорость выше. В этом случае концентрация и крупных, и мелких частиц малой плотности по-прежнему уменьшается, а частиц большой плотности возрастает к периферии потока;

• -    частицы мелкие, но плотные (или крупные, но легкие ) - ^Va ( P a + Р о ) < V B ( Р в + Р о ) могУт повести себя неоднозначно, например, возможен случай, когда мелкие частицы большой плотности начнут преобладать в области больших скоростей над крупными частицами малой плотности.

Изложенную выше физическую модель вполне можно применить к рассматриваемым нами мантийным породам. Как было отмечено выше, основу офиолитовых ультрамафитов составляют перидотиты, сложенные на 60-80% оливином, на 20-40% пироксенами (энстатитом (2035%) и диопсидом (до 10%)). Геологоструктурные и петрографические данные свидетельствуют о том, что наиболее мобильными являются оливиновые агрегаты, в предельном случае формирующие «слои» дунитов.

Из петрографических наблюдений мантийных ультрамафитов следует, что размеры структурных элементов деформации для сосуществующих оливина, ортопироксена и хромита не одинаковы. Пироксен в пластическом течении участвует в виде зерен или их крупных фрагментов (1-5 мм, в среднем 1,5-2 мм; ρ=3,2 г/см³), оливин – в виде субзерен со средним размером около 0,5 мм (ρ=3,2 г/см³). Подставим в полученное неравенство значения плотности и размеров частиц (структурных элементов деформации) минералов при условии, что дисперсионной средой является оливин. Для пары оливин ( Ol ) – ортопироксен ( Opx ) получим 0.04 « ( V oi /V opx )<((р орх +P 01 )/( O oi +P 01 )) ~ 1. Неравенство выполняется, следовательно, в областях с высокой скоростью потока должна быть выше доля частиц оливина.

В перидотитах помимо главных минералов (Ol, Opx, Cpx) присутствует глиноземистый хромшпинелид в количестве 0,n %, образующий обычно ксеноморфные выделения. По данным экспериментального плавления шпинелевых перидотитов [62, 75], этот минерал одним из первых (вместе с пироксенами) переходит в расплав. Вместе с тем в дунитах уже встречается и часто образует скопления вплоть до месторождений высокохромистый идиоморфный хромшпинелид (хромит). Таким образом, дуниты и хромититы сложены наиболее тугоплавкой минеральной ассоциацией, но всегда обнаруживают более высокую мобильность по сравнению с перидотитами: внедряются в последние, формируют штокверки. Кроме того, в строении месторождений хрома отмечается еще одна важная закономерность: мощные дунитовые тела обычно включают рассеянное оруденение с мелкозернистым хромитом, а тела небольшой мощности среди перидотитов вмещают массивные хромовые руды, сложенные средне- и крупнозернистым хромитом.

Все указанные выше закономерности объяснимы лишь с позиций реоморфиче-ского генезиса мантийных ультрамафито-вых комплексов. Рассмотрим этот вопрос подробнее. Акцессорные хромиты дунитов и бедновкрапленных руд мелкие (0,1-0,8 мм при среднем 0,5 мм; ρ=4,5 г/см³), в более концентрированных рудных телах размер зерен увеличивается до 0,5-3 мм, а наиболее крупнозернистыми являются массивные хромиты (2-10 мм). Тогда частицы хромита ( Chrt ) согласно неравенству 1=( V Ol /V Chrt )<(( ρ Chrt +ρ Ol )/(ρ Ol +p_O i )) « 1.2 должны преобладать в областях с низкими скоростями течения. С уменьшением относительного размера частиц хромита, участвующих в деформации, область распространения хромита может увеличиться.

Прогрессирующее пластическое течение уже расслоенных ультрамафитов может реализоваться в обстановке сжатия, что ведет к образованию на месте полосчатых дунит-перидотитовых комплексов сложных по строению сетчатых и шлиро-во-полосчатых образований того же состава. Деформация локализуется в более слабых (мобильных) дунитовых слоях, приводя к их растеканию, а перидотиты (обычно гарцбургиты) играют роль относительно жестких ограничений как для дунитов, так и для хромититовых тел, которые мигрируют внутри пластичной ду-нитовой оболочки.

Поскольку дунит и гарцбургит имеют постепенные переходы и различие в их реологии определяется количественными соотношениями между оливином и ортопироксеном, в ходе деформации происходит дальнейшее перераспределение зерен данных минералов: оливин стремится к формированию мономинеральных подвижных масс, ортопироксен также образует зоны обогащения вплоть до жил энста-тититов.

В итоге происходит будинаж компетентных гарцбургитов, наиболее крупные ослабленные зоны образуются по механизму трещин отрыва и заполняются реологически слабыми дунитами, они осложнены серией более тонких жил, образованных по механизму сколовых трещин. Формирующаяся таким образом структура соответствует картируемым на массивах гарцбургитового типа шлирово-полосчатым дунит-гарцбургитовым комплексам, в строении которых принимают участие крупные дунитовые тела, обрамленные густым штокверком маломощных дунитовых жил. Крупные обособления дунитов располагаются внутри зон интенсивного пластического течения с определенным шагом, который составляет около 10 км [33].

В хромовых рудах одновременно с ростом содержания рудных минералов увеличивается размер их зерен, а тела, сложенные густовкрапленными и массивными рудами, имеют тенденцию локализоваться вблизи компетентных гарцбургитовых экранов [17, 23]. Последнее объясняется тем, что согласно неравенству (13) при увеличении размеров структурных элементов деформации (зерен) хромита до 2

мм и сохранении таковых для оливина (0,5 мм), мы получаем 0.03125 = ( V Ol /V Chrt ) <( ρ Chrt +ρ Ol ) /(ρ Ol +ρ Ol )) ≈ 1.2, что говорит о сильном разделении в пластическом потоке данных минералов. Следствием этого в условиях сжатия является выжимание более мобильных оливиновых агрегатов в области с меньшим давлением, а залежи массивных хромититов ассоциируют с гарцбургитами, отделяясь от последних маломощной дунитовой оторочкой.

Таким образом, реоморфическая модель позволяет успешно объяснить все главные закономерности строения ультра-мафитовых массивов офиолитовой ассоциации. Надеемся, что дальнейшая разработка представленной модели может решить и более локальные проблемы, связанные с составом и строением рассматриваемых геологических объектов. К последним, в частности, относятся: 1) вариации состава и морфологии хромшпи-нелидов при переходе от лерцолитов к дунитам и хромовым рудам; 2) различный состав рудообразующих хромшпинелидов в различных массивах и их вариации в пределах крупных тел, а также ряд других.

Заключение

В работе обоснована принципиальная модель, способная объяснить закономерности перераспределения вещества верхней мантии в процессе становления офиолитовых комплексов и формирования рудных тел. Разработанная модель разрешает проблемы и противоречия, возникающие при допущении магматического или метасоматического способа образования рассматриваемых геологических объектов.

В текстурах и структурах ультрамафи-тов офиолитовой ассоциации запечатлены признаки пластического течения, которое являлось одним из главных факторов пет-рогенеза и рудообразования. Стратификация мантийного вещества, сопровождавшаяся, в частности, формированием тел хромититов, происходила при твердофазном перераспределении минералов в по- родах, представляющих собой дисперсионную систему. Первопричиной пластического течения и структурирования мог быть декомпрессионный подъем мантийного вещества в пределах рифтогенных структур и сейсмическое воздействие. Дальнейшее усложнение внутренней структуры и более глубокое разделение вещества, вероятно, происходило в обстановке сжатия, что, возможно, сопоставимо с современными геодинамическими обстановками в мантии преддуговых бассейнов.

Особенности деформационного процесса могли определяться воздействием различных физических полей: акустического (вибрационного, сейсмического), гравитационного, гидродинамического и гидростатического. Вероятнее всего, в природных объектах мы имеем дело с результатом комплексного воздействия (суперпозиции) данных факторов. При всех вариантах перечисленных воздействий определяющим параметром является размер частиц, для гравитационного, акустического и гидродинамического полей существенным фактором является плотность, а для гидростатического поля существенным фактором становятся и модули упругости компонентов породы. Подстановка в условия (12, 13) числовых значений физических свойств компонентов мантийных ультрабазитов позволяет получить решения, подтверждающие постоянную ассоциацию в рудных телах хромита с оливином. На основе предложенной модели возможно рассмотрение обратной задачи о том, какие условия могли привести к формированию рудных тел различного размера, морфологии и качественного состава хромитовых руд.

Работа выполнена при поддержке гранта «РФФИ-Поволжье», проект «№14-05-97001 р_повольжье_а»