Плазмон-поляритоны Дьяконова вдоль гиперболического метаматериала

В работе М.И. Дьяконова [1] рассмотрены поверхностные плазмон-поляритоны (ПП) вдоль границы одноосного кристалла и диэлектрика с диэлектрической проницаемостью (ДП) ε, когда оптическая ось параллельна плоскости раздела. Показано, что в случае ε|| > ε > ε⊥ возможно существование поверхностных волн, экспоненциально затухающих от границы и распространяющихся в некотором интервале углов относительно оси. Такие же волны исследованы в работе [2] на границе двух одноосных кристаллов, когда оси параллельны границе раздела и образуют между собой некоторый угол. При этом возникла необходимость представления поля через обыкновенную и необыкновенную волны. В работе [3] рассмотрены волны вдоль границы двух одинаковых анизотропных сред, в общем случае двуосных и немагнитных. Граница раздела получена поворотом двух полупространств с этими средами в разные стороны относительно нормали к ней. Волновод с двухосным диэлектрическим заполнением без диссипации рассмотрен в работе [4], а с одноосным заполнением – в [5]. В последнее время возник устойчивый интерес к гиперболическим метаматериалам (ГММ) из-за их весьма необычных свойств и ПП вдоль их границ. Обзоры по ГММ даны в работах [6 ‒ 9]. ГММ характеризуются большими значениями модуля волнового вектора |k| по сравнению с волновым числом k0, неэллиптическим (почти гиперболическим) уравнением Френеля для дисперсии необыкновенной волны, усилением ряда эффектов: Парселла, анизотропного сверхпланковского излучения, пространственной дисперсии (ПД) [9]. Идеальная поверхность изочастот в виде гиперболоида вращения имеет место в пренебрежении диссипацией и ПД, а реально эти яв- ления ее ограничивают [9]. Поэтому для создания ГММ в оптическом и мягком УФ-диапазонах требуются нанотехнологии с получением слоев порядка нескольких нанометров и менее. ГММ интересны как воноведущие структуры ТГц и оптического диапазонов. В работах [10 ‒ 13] рассмотрен диэлектрический волновод (ДВ), стенки которого выполнены из недиссипативного ГММ. Интересны ПП вдоль слоистых структур [14], поверхностей ГММ [15] и слоев асимметричных ГММ, прорезанных под произвольным углом к оптической оси [16, 17]. В [16] рассматривается аномальное поглощение в слое несимметричного ГММ, а в [17] – усиление отраженной и прошедшей волн в активном слое такого ГММ из графена за счет лазерной накачки. Использован метод матриц 4×4 Берремана. Выросший в последнее время интерес к исследованию ПП на границах периодических метаматериалов или фотонных кристаллов (ФК), а также вдоль метаповерхностей [14, 18] связан с новыми технологическими возможностями их изготовления и практическими потребностями их использования. В работе [19] рассмотрены недиссипативные ПП вдоль границы раздела гиромагнитного ГММ, описываемого диагональным двухкомпонентным тензором диэлектрической проницаемости (ДП) εˆ и гиротропным тензором µˆ . Такой ГММ интересен в плане перестройки дисперсии магнитным полем. Рассмотрена сложная поверхность изочастот в виде гиперболоида и тора, влияние фаз Берри объемных ПП на кираль-ные поверхностные ПП. Численные результаты решения дисперсионного уравнения (ДУ) не приведены. В работе [20] рассмотрены киральные ПП в двухосном ФК без диссипации, одна компонента ДП которого отрицательная, а две другие положительные и различные. В работе [21] использован разработанный авторами ранее способ гомогенизации для ПП в

ГММ. Потери не учитывались и численные результаты для дисперсии не приведены. В работе [22] рассмотрено управление дисперсией ПП в графеновом ГММ внешним постоянным электрическим полем. Оптическая перестройка волн в графеновом ГММ также рассмотрена в обзоре [23], оптически управляемые поверхностные ПП исследовались в работе [24], а объемные ПП – в работе [25]. Волновод в виде симметричного анизотропного слоя ФК без диссипации был рассмотрен в [26]. Диссипация в слоях ГММ в цитированных работах не рассматривалась.

Цель данной работы – рассмотреть диссипативные ПП на границе ГММ, включая случай слоя асимметричного ГММ и ГММ с произвольной ориентацией оси анизотропии. Численные результаты приведены для оси анизотропии, лежащей в плоскости ( x , z ) рис. 1. Получено также ДУ с произвольной ориентацией оси для толстого (полубесконечного) образца. Данная задача в известной литературе не решалась. Задача требует определения волн с комплексными постоянными распространения из комплексного ДУ. Общий случай образца конечной толщины требует поиска корней определителя четвертого порядка, имеющего громоздкий вид. Графическое представление решений такой задачи, зависящее от двух произвольных углов, может представлять отдельную задачу.

Волны вдоль поверхностей раздела диссипативных структур

В упомянутых выше работах диссипация не учитывалась, искались именно волны, локализованные у поверхности. Однако только такими волнами не исчерпывается спектр волн: при диссипации, кроме медленных поверхностных, возможны быстрые поверхностные втекающие волны, а из слоя конечной толщины возможно излучение быстрых вытекающих волн. Все такие комплексные волны также будем называть плазмон-поляритонами (ПП). В запрещенных зонах для поверхностных ПП (ППП) даже при отсутствии диссипации существуют решения в виде комплексных волн с комплексной продольной постоянной распространения и комплексными поперечными ее компонентами, а диссипация способствует переходу от одной ветви к другой через запрещенные зоны [14]. ППП существуют за счет полного внутреннего отражения. ПП возможны и при нарушении полного внутреннего отражения (НПВО), в частности, за счет потерь и втекания энергии. В ДВ (например, выполненных в виде слоя) возможны вытекающие антиповерхностные ПП. В такой волне НПВО происходит при уменьшении частоты ниже критической (на критической частоте фазовая скорость волны равна скорости света в вакууме), и в ней волна экспоненциально нарастает при удалении от поверхности [27]. Такое нарастание есть следствие экспоненциального убывания волны при движении вдоль слоя [27] при выполнении закона сохранения энергии. Вы- текающие ПП возможны в структурах, имеющих конечные (не нулевые и не бесконечные) поперечные сечения слоев. Из листа нулевой толщины (например, из листа графена) невозможно вытекание (если только он не активный, т.е. не оптически накачанный), поскольку нет запасенной энергии. В такой диссипативный лист волна может только втекать из вакуума (с обеих сторон). Из диссипативного полупространства невозможно вытекание в вакуум, поскольку при этом волна должна бесконечно нарастать вглубь.

Возможна только волна, втекающая из вакуума в полупространство [15, 27]. Это ППП, описываемый ДУ Ценнека k | z = k |0 ε / ( ε+ 1 ) . Таким образом, при учете диссипации есть медленные и быстрые втекающие ПП, а также быстрые вытекающие ПП. Если рассматривать недиссипативные полупространства с ДП ε , то вытекающие в них волны можно считать быстрыми по отношению к фазовой скорости c / ε , т.е. такая волна может с одной стороны втекать из вакуума и быть медленной, а с другой стороны вытекать в среду, если ее фазовая скорость удовлетворяет условию c / ε< v p < c . Подводя к такому волноводу призму с ДП ε , можно ее использовать для вывода или ввода энергии. Вместо призмы удобно использовать достаточно широкий ДВ со скошенным торцом, при этом ось ДВ должна быть направлена под углом вытекания. Таким образом, спектр комплексных ПП F ( ω , k )=0 состоит из ветвей, не имеющих разрывов в комплексном пространстве k , а при разрешении этого ДУ в виде k = k ' – i k '' = f ( ω ) ветви k ' = f ' ( ω ) и k '' = f '' ( ω ) не имеют разрывов в частотной области [14, 15]. В бесконечном недиссипативном ФК разрешенное относительно частоты ω = Ω ( k ) ДУ есть уравнение Френеля, которое при постоянстве частоты определяет поверхность изочастот в k -пространстве (здесь важно, что k = k ' , т.е. это действительное трехмерное пространство). В случае диссипации k -пространство шестимерное. В этом случае направление движения фазы v p = k' / |k' | , направление движения энергии ν e = S / | S | и направление движения диссипации v d = k " / |k " | в общем случае не совпадают. Без диссипации можно ввести вектор групповой скорости v g = ∇ k ω = ∇ k Ω ( k ) | k = k ' . Как градиент скаляра это полярный вектор, преобразующийся подобно вектору скорости. При этом возможны разрывы на кривых k ' = f ' ( ω ) в областях, в которых вектор v g не определен. Его использование проблематично не только в этих областях уже при малой диссипации, но и в других областях при существенной диссипации.

Будем рассматривать 1D одноосные ФК, содержащие металлические слои и называемые ГММ. При приведении к главной оси (ось направлена по оси z ) в ГММ имеем ε ⊥ = ε xx = ε yy , ε _|| = ε zz , ε′_⊥ε′ || < 0 . Здесь и далее штрих означает реальную часть. Для простоты будем рассматривать границу ГММ – вакуум, а решения уравнений Максвелла искать в виде:

E ( x , z , t ) = E exp ( i ( to t - k x x - k y y - k_zz ) ) ,

H ( x , z , t ) = H exp ( i ( to t - k x x - k y y - k_zz ) ) .

Подставляя их в уравнения Максвелла, имеем соотношения для амплитуд:

kzH - kvHz = tosos,,E,, z yyzxxx kxHz - kzHx = osp,, E„, x zzxxxy kyHx - kxHy = toSoSZZEZ,(1)

kyEz - kzEy = topoHx, kzEx - kxEz = top0Hy , kxEy - kyEx = top Hz.

Систему уравнений (1) можно записать в свернутом виде k H = toS ₀ S E , - k E = top / H , где использована эквивалентная оператору «ротор» при действии на плоскую волну матрица

- k z

k z 0

- k y

k x

k y

^- k x

странения   kz =± k0 Vs? -J 1 -(kx? + ky) / S||    являются объемными [29].

В качестве примера определения направления движения энергии рассмотрим объемный ПП в ФК, описываемом тензорами ДП S и магнитной проницаемости p . Пишем

E = ( toS ₀ ) ¹ S^{- 1} k H = - ( toS ₀ ) ¹ S ' k x H ,

H = - ( top ₀ ) ¹ p ¹ k E = ( top ₀ ) ¹ p ' k x E .

Для вектора Пойнтинга S =Re( E × H *) /2 имеем S = ( toS ₀ ) 1 Re ( S ¹ ( H * H _k - k H ² ) ) /2. Здесь n = k / k 0 -комплексный вектор замедления (векторный индекс рефракции), H ² = |H| ², H k = k - H . Далее все комплексные величины представляем в виде n = n ' – i n '' , где штрихом обозначена реальная часть, а двойным штрихом – отрицательная мнимая часть, векторными индексами обозначаем проекции. Имеем

H * H „ = H ' ( H n + H n ) - H" ( H n - H ‘ ) +

+ i [ H" ( H n ‘ + H n ) + H ' ( H n - H n- ) ] ,

Такая запись верна для любого (в том числе и недиа-тонального) тензора S, для которого система (1) несколько усложняется, а также и для магнитного ФК при замене I ^ p. Как нетрудно проверить, введенная матрица вырожденная и обладает следующимTи свойствами: матрица k2 не особенная и kS = -(Sk) . Это справедливо для любой симметричной матрицы S . В случае диссипации у такой матрицы smn = snm , т.е. должны быть симметричными действительные и мнимые части ее элементов. В этом общем случае кристалла с диэлектрическими S и магнитными p свойствами и в частном случае (1) равенство нулю определителя шестого порядка есть необходимое условие для существования однородного решения. Поскольку матрица k особенная, каждое из уравнений можно разрешить единственным образом, например, H = -(top0) kE . При подстановке в первое уравнение получаем однородную систему трех уравнений в векторной форме -k2E = k02SE и уравнение Френеля в виде det (k02 S - k) = 0 . Этот определитель третьего порядка, однако в него входят квадраты компонент. Максимальная степень у компонент k четвертая, а у волнового числа может быть шестой. Из другого уравнения следует E = (toS0) S 1 kH , система однородных уравнений (k02I - kS-1 k) H = 0 и уравнение Френеля det (k021 - kS1 k) = 0. Используя коммутационные свойства и симметричность тензора ДП, видим, что оба уравнения Френеля совпадают. Это имеет место и в более общем случае магнитодиэлектрического ФК, а также для бианизотропного ФК. Для одноосного ФК уравнения Френеля разбиваются на два [9, 28]: для обыкновенной волны kz2 = kо£± и для необыкновенной волны S-1 (kx? + ky ) + S!1 kz2 = k02. ПП с постоянной распро

( s ^{- 1} ) ( n ‘ H ² - H ‘ ( H n + H ; . ) +

S = £ H 1

+ H ‘' ( H n - H n -)) - ( s ^{- 1} ) " ( n H ² + +[ H '‘ ( H n + H ;. ) + H ’ ( H n - H n .) ] )

Здесь также обозначено ( S^{- 1} ) = Re ( S^{- 1} ) , ( S^{- 1} ) =- Im ( S^{- 1} ) . Полученное выражение для вектора Пойнтинга обозначим S h . С другой стороны, можно получить такой же вектор Пойнтинга S e , выраженный через поле E . Его получим, заменяя H ^ E , S - 1 ^p^{- 1} , p 0 ^S 0 . Очевидно, должно быть S e = S h . Для доказательства следует использовать векторные соотношения:

k -(E* x H) = cs0E*SE и k -(E x H*) = cp0H*pH , следующие из уравнений Максвелла, а также сопряженные им соотношения, следующие из сопряженных уравнений Максвелла. Имеем k - S = c (s0E*SE + p0H*p H) /4.

При отсутствии диссипации сразу следует условие

2 k - S = c s ₀ Re ( E * S E ) = c p ₀ Re ( H * p H ) .

Указанные уравнения удобны как дополнительные условия, накладываемые на тензоры при гомогенизации.

В электродинамике известна проблема определения плотности энергии, особенно при диссипации, поскольку конструкции типа WE =(ES*E* + E*SE) /4 и WH = ( Hp*H* + H*p H )/4 в общем случае ее не определяют [27, 28]. Проблема связана с запасенной энергией в веществе [27]. Поскольку перенос вещества в использованных балансных уравнениях не рассматривался, приведенные соотношения отвечают переносимой вдоль движения волны электромагнитной энергии. В случае соотношений типа (1) Se = cs0| n E 2-Re(E*(n*E))|/2. Видим, что в общем случае направление вектора Пойнтинга не совпадает с направлением движения фазы n', при этом, если n* -S<0, то волна обратная. Если совпадают направления n' и n'', а все проекции поля H на это направление равны нулю, то в этом случае

Г,.

S h = с Ц о H ² ( s ¹ ) n - ( e ¹ ) n

/2.

Однако это тривиальный случай изотропной среды. Для нее Sh = cЦоH2 (s'n' + s"n")/(2|s|2), и также следует Se = csoE2 (ц"n" + ц"n") / (2 |ц|2). При этом n = Vo д/ёЦ ,

H = ^ЦоЦ / (sos)E , поэтому Sh = Se. В изотропном случае имеем n = ^(sV-sV')- i(е'ц' + ц'е'), n* = ±^(sV -s"Ц )2 + (sV + ^s ")2 + (s^ - s"Ц ) ,(3) n" =   (УЦ - s"ц")2 + (sV + ^s")2 - (УЦ - s"ц"") .

Знак в (3) определяется условием n'' >0, и формально отрицательный знак возможен, только если одновременно s " <0 и Ц " <0. Однако такие изотропные метаматериалы не достижимы, а условие ц "  <0 невозможно и для пространственно однородных сред [30]. Следовательно, однородная плоская волна в изотропной однородной среде всегда прямая. Однако на границах сред возможны комбинации неоднородных плоских волн, при этом движение энергии пограничной волны вдоль заданного направления получается путем усреднения вектора Пойнтинга по поперечному сечению и направлениям k ± . В этом случае вектор k || = k z задает это направление движения. Он может быть выбран вдоль любой из осей (взята ось z ), а условием обратной волны является условие k " k z <  0 [15]. Оно говорит о том, что фаза и энергия движутся в разные стороны, а движение энергии совпадает с направлением движения затухания.

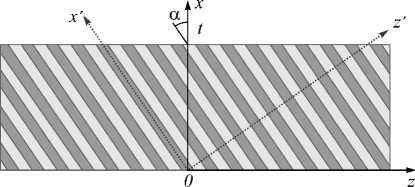
Рис. 1. Слой ГММ с повернутой осью анизотропии (3)

Постановка задачи и ДУ

Нас будут интересовать поверхностные E-волны (ТМ-волны) относительно оси z , идущие вдоль поверхности ГММ рис. 1, для которых H z =0. На этом рисунке ось z и ось анизотропии z' лежат в одной плоскости и повернуты в ней на угол α (нормаль направлена по оси x ). В таком случае при H z =0 это E-волны (ТМ-волны) относительно оси z. В случае произвольного угла поворота оси z (относительно оси x ) волны вдоль нее гибридные, состоящие из E-волн и H-волн (необыкновенной и обыкновенной волн в терминах кристаллооптики). Тогда в ГММ следует использовать их комбинацию и все уравнения (1). Такой случай рассмотрен ниже. В системе координат, связанной с осью анизотропии, имеем две компоненты тензора ДП: s xx = s yy , s zz . Наиболее простой случай имеет место при а = 0 (для него штрихи будем опускать). Далее такое обозначение соответствует нулевому углу. В исходной системе координат при а ^ 0 компоненты тензора ДП будем помечать тильдой. Для H-волны E z = 0, и в этом случае ДУ H-ПП становится совсем простым: таким же, как в изотропной пластине с ДП s xx . В случае движения ПП нормально к плоскости рис. 1 (когда ось z расположена нормально) тензор ДП преобразуется применением матрицы поворота на угол ф = п/2 относительно оси x . При α = 0 ДУ ПП вдоль оси y получим заменой s zz ^s yy . В общем случае гибридного ПП необходим поворот на два произвольных угла относительно двух осей y и x .

В случае рис. 1 и α = 0 имеем k0syykyEz / Z0 - kxkzHz k02syy - kz        ’ kykzHz + k0 (kxs + kzsc EE/ / Zo yz z xxx zxz z

E_x = x

E y

Аналогичные связи можно написать для случая E z =0. Для волны в вакууме k ₀ ² = k x ₀ + k .2 + k_z² . Отношения в (3) являются волновыми сопротивлениями. Первое и третье волновые сопротивления соответствуют переносу энергии вдоль границы соответственно вдоль осей y и z , а второе – в перпендикулярном к ней направлении вдоль x . ДУ ПП вдоль границы раздела x= 0 получается сшиванием. Сшиванию полей соответствует согласование волновых сопротивлений при движении вдоль оси x [15]:

к 02 - k Z k x 0

^к 02 ^е xx ^- k ²

кх ^хх xxx

При этом достаточно использовать по одной волне в каждой среде. Равенство (4) и есть ДУ ПП вдоль поверхности. Оно может быть записано в виде

к 02 - kZ к0 - k2 - kZ

ко2бxx - kZ е^ х к,°8„ - szz / е^к2 - к2 xx zz zz xx z y

Это биквадратное уравнение относительно kz. При ky =0 оно имеет простое решение kz = ± к0 е xx (е zz -1) / (е xx е zz -1).

В случае однородной среды еxx = еzz = е оно описывает дисперсию ПП Ценнека kz = ±к0 ^е / (е +1) . В случае поворота границы раздела на угол п /2 относительно оси у в ДУ ПП (5) следует сделать замены еxx ^еzz: kz = ± к о ^е zz (е xx -1) / (е xx е zz -1) . В этом случае кристаллическая ось z' перпендикулярна границе раздела, и все направления движения равноправны. Для ПП вдоль оси y также имеем ку = ±ко а е22 (е^ -1) / (е^е^ -1). yzzxxxxzz

Гомогенизация периодической плоскослоистой среды из двух компонент в виде слоя металла с ДП е m и слоя диэлектрика с ДП е d в приближении без учета пространственной дисперсии дает е xx' = е m K m + е d K d , е - Х - = ( е _т¹ K m +е - 1 K_d ) . В случае одинаковых коэффициентов заполнения K m = K d = 1 /2, d m = d d = d /2, где d – период, d /2 – толщина слоев, имеем

cos2 (а)е xx + sin2 (а)е zz0

sin (а) cos (а)(е zz-е xx)

еxx' = (еm + еd)/2, еz'z' = 2еmеd/(еm + еd). ДП металла оцениваем по формуле Друде –Лоренца еm = еL - top / (ю2 - iгоюc).

Далее, наряду с волновым числом к ₀ = to / c , будем использовать плазменное волновое число k_p = to p / c . В пренебрежении диссипацией (при нулевой частоте столкновений to _c = 0) е _m = е L - to p / to ² . На низких (по сравнению с плазменной частой) частотах to < to _p / JZ 7 компонента е xx отрицательная, если е _m <- е _d . При этом е _zz > 0. Если же е _m <- е _d , то е xx' > 0 и е _z z <0. Первый случай соответствует ГММ второго типа, а второй – ГММ первого типа [9]. Отметим, что эти условия легко можно уточнить при учете диссипации, т.е. при конечном значении частоты столкновений to c , при этом следует говорить о значениях реальных частей е x _x - и е Z - _Z - . Учет пространственной дисперсии возможен по формулам (20), (21) из работы [9]. Гиперболическая дисперсия означает волны с высоким значением |k| = k >>  k 0 (high- k waves). Однако неограниченных значений быть не может. Имеет место ограничение к <<2 п / d , связанное с гомогенизацией, а также ограничение, связанное с диссипацией. Последнее при комнатной температуре более сильное. Оно может быть снижено использованием сверхнизких температур, и тогда при периоде в несколько нанометров можно ожидать достижение максимальных значений k ~0,1 нм ^{– 1}. Мы будем рассматривать асимметричный ГММ, ось которого повернута на угол α. Матрица поворота вокруг оси y на угол α имеет вид:

Ту (а) =

cos ( а ) 0

sin ( а ) 0

- sin ( а )

cos ( а )

Действуя на вектор E , она дает:

E x = E_x cos ( а ) - E_z sin ( а ) , E' y = E y ,

Ez = Ex sin(а) + Ez cos (а), т.е. имеет место поворот против часовой стрелки. При этом исходная матрица ДП в повернутой системе преобразуется как е = Ту1 (а)еТу (а) = Т(-а)еТ(а) или

sin ( а ) cos ( а )( е zz -е xx )

cos ² ( а ) е zz + sin ² ( а ) е xx

При таком повороте в соотношениях (1) следует учесть недиагональные компоненты тензора (7). В случае движения ПП вдоль оси z имеем ДУ р0 = р, где р0 = V1 - kz2 / к02 , р = (е xx - kz / к02) / а , а=е xx е zz - е x,.

Это уравнение также можно разрешить относительно k z . Если рассмотреть задачу о слое несимметричного ГММ толщины t , то следует учесть волны двух направлений вдоль оси x с различными значениями k x , но с одинаковыми волновыми сопротивлениями, и тогда сшивание полей приводит к ДУ вида

2 рр 0 в = р ² +р 0 , (8)

распадающегося на два: р о =р ( р±7Р 2 - 1 ) . Здесь

exp ( - ik X t ) + exp ( - ik_xt ) exp ( - ik X t ) - exp ( - ik x t ) ’

при этом kx = — kzexz / eXX ± ^(koSXX - kz )A / exx.

В случае симметрии e _xz = 0 , k X = - k x , P = i / tan ( k x t ) и ПП имеют либо электрическую, либо магнитную стенки в центре слоя. В этом случае ДУ имеют вид

Ро = р(itan(kxt /2)) , где верхний знак соответствует «электрической стенке», а нижний – «магнитной стенке».

Рассмотрим теперь ПП, движущийся под углом к оси z вдоль границы такого асимметричного ГММ. Задачу можно решить путем еще одного поворота системы координат вокруг оси x на угол ф , образуемый новой осью z'' со старой осью z . Тогда k y'' =0, но тензор ДП приобретает сложный вид. Матрицу поворота

Новая ДП e имеет полностью заполненную симметричную матрицу. ДУ для мод вдоль такого слоя можно построить, используя матрицу передачи 4 × 4 Бер-ремана для анизотропного слоя. Она связывает поля по обе границы слоя, и, налагая условия излучения (втекания или вытекания), получаем довольно громоздкий вид ДУ в виде равенства нулю определителя четвертого порядка, который мы не приводим.

Мы рассмотрим более простое решение этой задачи в старой системе координат, непосредственно используя сшивание и считая слой толстым. Здесь уже нужно учесть две волны E и H вдоль оси z при наличии компоненты k y . Выражаем все поля в ГММ через AE z и BH z (с произвольными амплитудами A и B ). В вакууме берем поля с другими помеченными нулем амплитудами: A 0 E z и B 0 H z . Сшивая компоненты E z , H z , E y , H y , получаем однородную систему линейных уравнений. При сшивании E z и H z сразу имеем A 0 = A , B 0 = B , что снижает размерность. Для поперечных компонент получаем

E x

( k x k_z - k 0² S xz ) E z + Z 0 k 0 k y H

22 k z    k 0 ^e xx

Tx (ф) =

cos ( ф ) sin ( ф )

- sin ( ф ) cos ( ф )

следует применить к ДП (7):

S = T - ( ф ) е T x ( ф ) .

E y

kzkvEz - ZokokxHz zyz x z kz - k2e ....

k x k z H z - k 0 Ё yy k y E z / Z 0

kz - k2e yy        ’ kykzHz + k0 (sxxkx + sxzkz ) Ez / Z0 kz - k2e xx

ДУ для такого ПП имеет вид

( k z k y ) ² k 0²

k_{x 0}          k_x     Ve xx k x +e _xzk_z     k_{x 0}

k z - k 0²    k z - k 0² e yy Д k z - k 0 e xx     k z - k 0²

[ ( k z - k 0² ) ^{- 1} - ( k z - k 0² e xx ) ^{- 1} ] [ ( k z - k 0² ) - ( k z - k 0² e yy ) ^{- 1} ]

Оно описывает гибридные моды с компонентами ky и kz, распространяющиеся под углом к оси z. Входящую в это ДУ величину kx следует находить из уравнения Френеля общего вида. В частных случаях ДУ (9) упрощается. При kz =0 или ky =0 левая часть (9) обращается в нуль, уравнение Френеля также упрощается, а ДУ распадается на два для ПП, движущегося вдоль оси y, и два для ПП вдоль оси z. В первом случае это ПП, движущийся перпендикулярно оси анизотропии. Во втором случае имеем два ДУ kz = k02 (kx - kx0Syy) / (kx - kx0) и

(exxkx + exzkz)(kz - k02) = kx0 (kz2 - k2еxx), а движение идет в плоскости оси анизотропии. При симметрии k2 =ezz (k02 - kz / sxx) и первое уравнение при α =0 приобретает вид kz = k02 (e xx - s zz) / (e xx - e zz).

Это H-ПП. Соответственно, второе уравнение описывает E-ПП, который рассмотрен выше. В случае k z =0

первое уравнение имеет вид k_{x 0} = k_x / e yy . Оно упрощается при α= 0:

k y = k ₀ ² ( S xx -e _zz ) / ( S xx - 1 ) .

В этом случае второе уравнение превращается в соотношение k x = k x 0 , не имеющее решений. Можно получить упрощения ДУ и для случая а = п /2.

Представление поля внутри слоя через моды E и H эквивалентно распространению в слое в двух направлениях обыкновенной и необыкновенной волн, но более удобно. Для обыкновенных волн вектор E лежит в плоскости, перпендикулярной оси анизотропии, поэтому произвольное направление этого вектора требует введения двух волн: обыкновенной и необыкновенной. Конечность слоя означает необходимость введения волн с двумя поперечными компонентами волнового вектора. Разделение ПП на обыкновенный и необыкновенный для асимметричного ГММ в общем случае не происходит, но возможно в частных случаях при а =0 и а = п /2.

Плотность энергии в метаматериале

Плотность энергии для дисперсии среды, описываемой ДП s m ( to ) c законом Друде -Лоренца, известна. Считаем, что резонансные частоты в члене s _L ( to ) лежат существенно выше рассматриваемой частоты to и почти не оказывают влияние, т.е. s _L ( to ) = s _L = const. Поэтому плотность энергии в металле описывается выражением W = W e + W m , в котором

W e =S o [s l +to p / ( to ² + to 2 ) ] E ² /4, W h =Ц о Н ²/4.

Поскольку H = ^s ₀ ( s' _m - i s" _m ) / ц ₀ E , то для металла W m =S o [ 2 s L -s' m + ^ + C ] E 2 /4. (10)

При отсутствии диссипации имеем W_m = s ₀ ( s _L + |s' _m I) E ² /2 ниже частоты to _p / J& t , а выше нее W_m = s ₀ s _L E 2 /2. Считаем, что и диэлектрик описывается формулой Лоренца, все резонансные частоты которой также лежат далеко. Тогда W d = s ₀ s d E 2 /2, и полная средняя за период плотность энергии в ГММ дается формулой W HM =( W m d m + W d d d )/ d .

Численные результаты

Мы рассматриваем металлические слои с параметрами s l = 9,0, to p = 1,36 ■ 10¹⁶, to c = 2,8 ■ 10¹⁴ Гц и диэлектрические слои с s d = 3,0. Для использования длин волн вплоть до 300 нм достаточно взять период d ~10 нм. Слой асимметричного ГММ представлен на рис. 1. Он является волноводом для ПП вдоль оси z . Результаты численного итерационного решения ДУ (8) приведены на рис. 2 и 3 для разных углов α и разных ветвей ДУ (знак « + » и «-» в формуле для Р ). В случае симметрии рис. 2 соответствует магнитной стенке в центре слоя, а рис. 3 – электрической стенке в центре слоя. В случае металлической пленки это соответственно антисимметричные и симметричные ПП (по компоненте H y ). Стрелками показаны места вставок более детальных графиков. На дисперсионных ветвях имеются участки, для которых ПП обратные, причем как медленные, так и быстрые. Для рис. 3 такие участки характерны для медленных ПП.

Итерации сходятся до значений нормированной невязки порядка 10 –10, однако скорость сходимости разная: от нескольких единиц до нескольких тысяч итераций. Для решения ДУ использован метод минимальных невязок с коррекцией сходимости: параметр итерации на каждом шаге подбирался из условия равенства нулю производной правой части итерационной формулы, что обеспечивает сходимость. Однако она может быть медленной, когда параметр итерации мал, поэтому использовался алгоритм его корректировки, позволяющий снизить максимальное число итераций до нескольких сотен. Определение оптимального параметра итерации производилось мето- дом релаксации и требовало вычисления производной функции, определяющей ДУ. При слабой диссипации отрицательная ДП слоев металла создает поток мощности в металлических пленках, противоположный движению фазы и потоку в диэлектрике и в вакууме, что может приводить к обратным ПП. В областях сильных потерь (около плазмонных резонансов) ПП прямые. Поворот оси позволяет управлять дисперсией. Замедление в симметричной структуре рис. 1 несколько больше замедления в сплошной металлической пленке той же толщины.

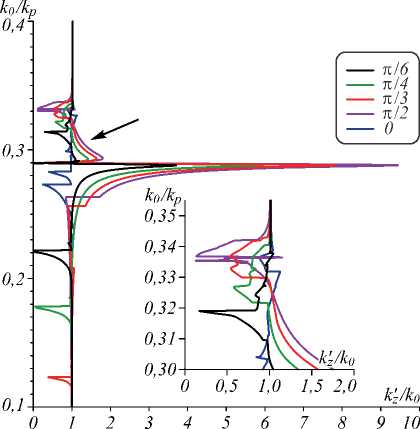
Рис. 2. Дисперсия замедления в слое ГММ толщины 50 нм при разных углах α: ветвь ДУ со знаком “+”

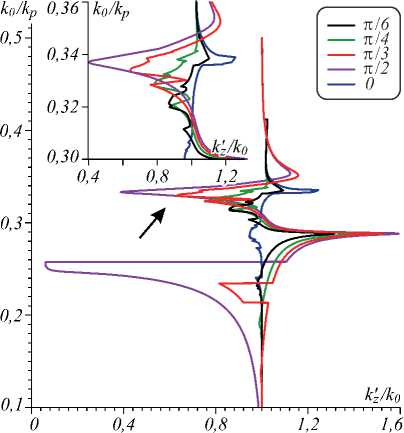
Рис. 3. Дисперсия замедления в слое асимметричного ГММ толщины 50 нм при разных углах α: ветвь ДУ со знаком “‒”

Результаты расчета дисперсии и потерь для ПП вдоль границы полубесконечного образца ГММ при а = 0 и а = п /2 приведены на рис. 4, 5 и 6. Часть кривых левее n' = 1 соответствует быстрым втекающим волнам, а правее – медленным. Волны в плоскослои- стой среде c а = п /2 более медленные, а в области выше частоты плазмонного резонанса обратные. Это отличает плоскослоистую среду от сплошной металлической, для которой обратных волн нет. Для ГММ с а = 0 обратных волн нет, а максимальное замедление соответствует более высоким частотам, для которых ет > 0 . Кривые построены так, что k'> 0, поэтому обратным волнам соответствуют как бы отрицательные потери. Часть из ветвей на рис. 2, 3 также соответствует обратным волнам, при этом быстрым ветвям (n' < 1) соответствуют вытекающие волны. Все приведенные кривые не имеют разрывов и получены путем решения ДУ при плавном изменении частоты. Было использовано несколько тысяч частотных точек, поэтому все ветви с резким переходом от нормальной дисперсии к аномальной отрицательной дисперсии и наоборот имеют не менее 5 точек. Резкие переходы обусловлены малой диссипацией. Увеличение диссипации (загрубение) сглаживает кривые. Отсутствие диссипации приводит к появлению запрещенных зон. В них kz мнимые, а волны эванесцент-ные. Для толстой подложки рис. 4 ‒ 6 проявляется только один резонанс, и кривые более гладкие. Рис. 6 соответствует ПП типа Ценнека [15], при этом аномальной отрицательной дисперсии соответствует прямая волна, потери максимальны при резонансе и высокие в области аномальной дисперсии (запрещенной зоне). В вакууме энергия всегда переносится вдоль движения фазы. Наличие обратных волн – это интегральный эффект, связанный с тем, что в металлических структурах компонента вектора Пойнтинга может менять знак при е'т < 0 , а полный поток энергии дается интегрированием компоненты Sz по поперечному сечению и есть разность двух противоположных потоков.

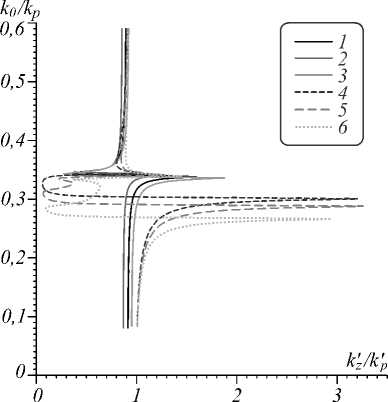
Рис. 4. Дисперсия E-ПП вдоль полупространства ГММ со структурой, соответствующей α = 0 (кривые 1 ‒ 3) и а = п /2 (кривые 4 - 6): зависимость нормированного волнового числа от замедления n ' = k ' /k₀ при разных

ДП e d : 2 (кривые 1 - 4), 3 (кривые 2 - 5) и 5 (кривые 3 - 6)

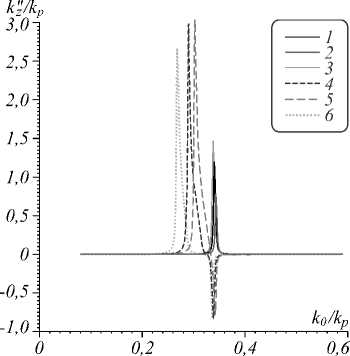
Рис. 5. Нормированные потери k ' / k p E-ПП вдоль полупространства ГММ, соответствующие дисперсии рис. 3 для а = 0 (кривые 1 - 3) и а = п /2 (кривые 4 - 6) в зависимости от нормированного волнового числа k0 / kp при разных ДП e d : 2 (кривые 1 - 4), 3 (кривые 2 - 5) и 5 (кривые 3 ‒ 6)

В области плазмонного резонанса k ' « k ' ~1/ Vs", т.е. для получения больших замедлений следует снижать диссипацию. Оценка для первой структуры дает в области резонанса k_z = k ₀ ( 1 - i ) ^ ( 1 + е d ² - 2/ е d ) / е'' / 2 . Для второй структуры рис. 4 имеют место два резонанса: низкочастотный с k_z = k ₀ ( 1 - i ) е d / ( 1 + e d ) е" при е m ® - е d , и на более высокой частоте с k z = k 0 ( 1 + i ) ( 1 + е 5 -е d ) / [ ( 1 + е 5 ) 2 е''] , при е m « 1 / е d . Непосредственно видно, что последний соответствует обратному ПП. Все ПП на рис. 4 ‒ 6 втекающие, поскольку вытекание из диссипативного полупространства невозможно.

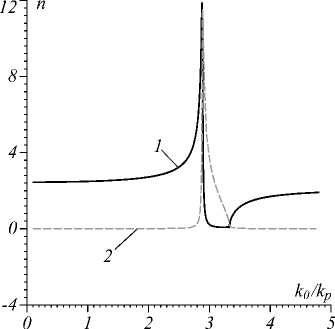
Рис. 6. Комплексный коэффициент замедления n = n’ ‒ in” в слое ГММ толщины 5000 нм при а = п /2 в зависимости от нормированной частоты: n’ – кривая 1, n” – кривая 2

Заключение

В работе с использованием простейшей гомогенизации получены точные решения для плазмон-поляритонов Дьяконова вдоль поверхности в общем случае асимметричного слоя гиперболического мета- материала в виде плоскослоистой периодической ме-талл-диэлектрической структуры, ось анизотропии которой лежит в плоскости распространения и повернута относительно оси распространения. Рассчитаны дисперсии ПП вдоль слоя конечной толщины и полупространства из такого ГММ, а также потери. Получены дисперсионные уравнения и для движения ПП под произвольным углом вдоль границы полупространства асимметричного ГММ. Учет пространственной дисперсии, т.е. зависимости е(к0,kx,kz) возможен, но приводит к сложным нелинейным дисперсионным уравнениям и уравнениям Френеля, анализировать которые возможно только численно. Как пространственная дисперсия, так и диссипация искажают гиперболический закон дисперсии и ограничивают по модулю компоненты волнового вектора объемных волн, т.е. замыкают поверхность изочастот.

Найдены условия существования медленных и быстрых, втекающих и вытекающих, а также прямых и обратных поляритонов. Рассмотренный волновод в виде слоя асимметричного гиперболического метаматериала может быть использован в оптическом, ИУ- и ТГц-диапазонах. В качестве реализации ГММ в ТГц-диапазоне удобно использовать структуры с листами графена. В таких ГММ возможна компенсация потерь при применении лазерной оптической накачки в видимом диапазоне. Потери играют существенную роль при возбуждении и распространении ПП [9, 14, 15, 24]. Они максимальны при максимальном замедлении. Пренебрежение диссипацией приводит к появлению запрещенных зон в области быстрых вытекающих волн с отсутствием в них действительных решений. Следует отметить, что ПП без диссипации вдоль поверхности анизотропных кристаллов рассматривались еще в обзоре [31]. Анализ потерь требует определения комплексных корней, что усложняет численное решение. Однако такой анализ позволяет определить направление затухания волн и классифицировать их как прямые или обратные, что существенно проще, чем вычисление вектора Пойнтинга. Обратные ПП интересны для фокусировки ПП на поверхности. Приложение внешнего магнитного поля (например, вдоль оси ГММ) позволяет создавать невзаимные волноведущие структуры.

Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию (проект № FSRR-2020-0004).