Площадь питания дерева как фактор его роста

В лесоведении сложилось убеждение, что развитие, прирост и в целом размеры деревьев в древостое в значительной степени зависят от площади питания дерева [Assmann, 1961; Поляков, 1973; Мартынов, 1976; Тябера, 1982; Сеннов,1999; Нагимов, 2000; Плантационное…, 2007]. Исследование средней площади питания деревьев или густоты древостоя, как внутреннего биотического фактора, позволило установить закон морфогенеза одноярусных древостоев Г.С. Разина, по которому каждый древостой один раз достигает максимума в своем развитии, после чего снижает прирост тем раньше и сильнее, чем больше была его начальная густота [Разин, 1979; Рогозин, 2018а].

Доказано, что средняя площадь питания дерева (густота древостоя) определяет размеры деревьев,

например, в насаждениях сосны с силой 88–94% [Нагимов, 2000]. Однако касательно индивидуальной площади питания дерева, например в микроценозах, нет ясности. Неизвестно, с какой силой она влияет на размер дерева в сравнении, например, с влиянием генотипа дерева. Если установить их более или менее точные значения, то на более сильный из них как раз и следует воздействовать в первую очередь для увеличения продуктивности дерева и древостоя в целом.

Поясним, что есть сильнейшие отличия в расчетах «средних» и «индивидуальных» площадей питания. Первая отражает действие фактора густоты на уровне всего фитоценоза, и данных по этой позиции достаточно, в особенности для лесных культур [Поляков, 1973; Мартынов, 1976; Маслаков, 1984; Плантационное…, 2007; Голиков, 2014], тогда как для второй величины, действующей как фактор на уровне отдельных деревьев, исследований немного, а методы различны [Марченко, 1995; Горячев, 1999; Грабарник, 2010; Борисов и др. 2014; Вайс, 2014]. Так, из данных обширного исследования на эту тему [Нагимов, 2000, с. 305] следует, что в методе обычных полигонов питания корреляционные отношения между площадью питания и приростом дерева были в среднем равны всего лишь 0.27. Влияние второго фактора, а именно генотипа дерева, на индивидуальные размеры деревьев сосны составляет, по данным генетиков-селекционеров, от 20 до 40% [Исаков, 1999; Тараканов и др., 2002; Тараканов, 2003; Царев, 2013]. В итоге получаем теоретически примерно равную силу влияния генотипа и площади питания дерева на его размер. В сумме они составляют около 60% и остается еще 40% влияния неучитываемых факторов.

Данные эти справедливы для сосняков в молодом и среднем возрасте, и неясно, какими они будут в спелом возрасте, когда цикл развития фитоценоза завершается. Можно предполагать, что с возрастом влияние индивидуальной площади питания будет слабеть, так как все типы размещения деревьев в древостое – случайный, кластерный и равномерный существуют как необходимые элементы его структуры до возраста спелости [Нестеров, 1961; Маслаков, 1984, 1999; Марченко, 1995; Сеннов, 1999]. О них известно давно, но до конкретных расчетов силы влияния факторов, вызывающих образование столь разнообразных структур, дело еще не дошло. Происходит лишь фиксация типов расположения деревьев с самым общим объяснением причин их появления на основе парадигмы конкурентного давления и естественного изреживания где, как ни странно, нет выясненных долей влияния этих факторов, несмотря на то, что их рассматривают в качестве основных при модельном подходе [Грабарник, 2010]. Можно согласиться, что случайный тип размещения возникает в результате конкуренции. А кластерный тип? Ясного ответа пока нет, и о причинах столь сложной структуры даже самых простых насаждений по-прежнему известно немного, что обусловливает актуальность ее изучения самыми разными методами.

Мы проводили работы в наиболее старом из обследованных вблизи г. Перми лесов, в древостоях сосны обыкновенной ( Pinus sylvestris L.). Их изучение нужно для представления о том, до какого предельного возраста они еще могут выполнять свои средообразующие функции. В этой связи важно выяснить их структуру, которая будет так или иначе отражать завершение жизненного цикла развития древостоя сосны, когда конкуренция между деревьями верхнего яруса ослабевает.

Цель исследования – выяснить силу влияния индивидуальной площади питания дерева на его размеры в спелом насаждении как фактора в количественном выражении.

Выбор метода исследования

Теоретически важно понять, как дерево использует доставшуюся ему площадь питания и каких достигает размеров к возрасту естественной спелости без насильственного увеличения размеров личного пространства. Средняя площадь питания в растениеводстве рассчитывается весьма просто: через густоту стояния растений на единице площади [Синягин, 1975]. Иное дело в лесоводстве, где определяют индивидуальную площадь питания каждого дерева, применяя более сложные методы полигонов с учетом расстояний до „соседей“. Мы провели их анализ [Рогозин, 2018 б ], где рассмотрели следующие методы: измерение расстояний между деревьями, полигоны роста с простым делением расстояний между „соседями“, полигоны с делением расстояний между „соседями“ пропорционально их диаметрам и выборочные круговые площадки, подробно описанные З.Я. Нагимовым [2000], а также метод «социальных групп» с отношением суммы диаметров крон соседствующих деревьев к диаметру кроны центрального дерева [Вайс, 2014]. Рассматривались также длительные опыты по рубкам ухода с увеличением площади питания в среднем возрасте насаждений [Сеннов, 1984, 1999].

Критический анализ этих работ показал, что если в них оговаривалось и принималось положение о том, что чем больше размеры деревьев, тем больше и приходящиеся им площади питания, то тогда для оценки влияния площади питания на прирост дерева использовали три зависимых переменных величины: текущий прирост дерева по диаметру (величина 1); размер дерева (величина 2); площадь питания дерева, определяемая по расстояниям от „соседей“ пропорционально их размерам (величина 3). Так как первая и третья величины зависят от второй (являются частью этой второй величины), то первая величина будет зависима от третьей. Но тогда пропорциональная пло- щадь питания как фактор оказывается уже не пригодной для выяснения силы ее влияния на размер дерева. Поэтому независимой переменной величиной в площади питания дерева будет, по нашему мнению, ее значение, определяемое по полигонам с простым делением расстояний между „соседя-ми“. Иными словами, следует выяснить, как дерево распорядилось доставшейся ему ранее площадью, причем безотносительно к размерам соседствующих деревьев, которые признаются в прошлом потенциально равными в освоении этой доставшейся им лично площади питания. Еще одной независимой переменной может быть среднее расстояние до ближних „соседей“ (обычно 7–10), а также расстояние до самого ближнего „соседа“. Эти величины (площадь питания и расстояние до „соседей“) могут выступать как факторы. И по ним уже можно будет корректно рассчитать силу их влияния на размер дерева. Все другие методы оперируют уже зависимыми переменными величинами, и они не могут выступать в качестве факторов [Рогозин, 2018б].

Поэтому в настоящей работе мы выбрали метод обычных полигонов питания для центрального дерева с простым делением расстояний на 1/2 к его „соседям“, известный как метод Брауна [Нагимов, 2000], а также использовали среднее расстояние до 7–12 соседствующих деревьев.

Материал и методика

Использовано перестойное насаждение сосны обыкновенной ( Рinus sylvestris L.) в Пермском городском лесничестве (леса г. Перми), в кв. 1 бывших лесов завода им. С.М. Кирова (ныне кв. 61 Нижне-Курьинского участкового лесничества), южнее остановки автобуса «ТЭЦ-14». Здесь на площади 2 га обнаружены деревья с диаметрами до 68 см. Древостой оставляет хорошее впечатление; его структура не нарушена, так как вывозку древесины от санитарных рубок осуществляли по просветам между деревьями.

Были заложены две пробные площади: участок «Южный» и участок «Северный» площадью 1.094 и 1.109 га соответственно, примыкающие друг к другу. Каждое дерево, всего 736 шт., нанесли на план с точностью ±10–35 см, которая была определена при перекрестных линейных засечках, а также после распределения невязки всего полигона в масштабе 1:100. Взаимное расположение деревьев в биогруппах определялось точнее (± 3–5 см). Для работы карта была оцифрована в программе ArcGIS с использованием 60 шейп-файлов. На каждом дереве делали отметку на высоте 1.3 м, где измеряли окружность ствола с округлением до 0.5 см, после чего расчетным путем определяли диаметр с округлением до ± 0.1 см. Возраст определили в 2017–2018 гг. по кернам древесины на высоте 1.3 м. Всего изучили 21 керн от средних и крупных деревьев. К слоям древесины на керне добавляли 7 лет, считая, что за это время сосна здесь могла достигать высоты 1.3 м. Возраст сосны оказался в среднем 184 года, с колебаниями от 174 до 195 лет. Выяснили, что сосна заселяла эту территорию с 1823 г. и период заселения составил 21 год. История заселения участков сосной связана со сплошной рубкой леса и выжиганием угля на этой территории в 1820-е гг.

Таксационная характеристика участка «Южный», где были проведены исследования, оказалась следующей. Состав 10С, ед. Е. Возраст 184 года, средняя высота 32 м, средний диаметр 39.8 см, сумма площадей сечения 42.8 м²/га, полнота 0.91, запас 610 м³/га. Единично встречается ель с диаметрами 20–45 см. Тип леса – сосняк кислич-никовый, в кустарничниковом ярусе преобладает черника (70%) и брусника (30%). Местоположение ровное, с поднятием территории на 1.5–2.0 м в западной части; тип условий «свежий бор» (В 2 ), почва супесчаная, класс бонитета 1. Текущая густота 344 шт./га. Есть подрост ели густотой 0.3–1.5 тыс. шт./га высотой 2–5 м в возрасте 35 лет, который появился после низового пожара 1982 г. Санитарное состояние сосны, с учетом её возраста, хорошее; имеются стволы с наличием плодовых тел сосновой губки (9%). В 2003 г. (14 лет назад) здесь прошел ветровал с вывалом 6.8% деревьев. Частоты деревьев по диаметрам соответствуют нормальному распределению.

Методика выстраивания полигонов питания подробно описана в литературе [Тябера, 1976; Усольцев и др., 2018]. В нашем случае эту работу мы начинали с выбора модельного дерева, после чего на готовом плане расположения деревьев его соединяли линиями с 3–8 соседствующими деревьями. На этих линиях-лучах находили середину и отмечали ее крестиком (рис. 1).

Далее от крестика в обе стороны прокладывали перпендикулярные линии до соединения с такими же линиями от соседнего луча. В результате получали многоугольники разной формы. Там, где были прогалины, правило перпендикулярности нарушали, так как требовалось свести вместе до 6–7 полигонов, причем в точке, от которой до деревьев по краю прогалины было бы примерно равное расстояние. Вторым моментом было нахождение «точек компромисса» в районе расположения биогрупп. Всего таких точек компромисса, обозначенных более жирным крестиком, на рисунке показано четыре (рис. 2).

Результаты исследований

Изучение расстояния до „соседей“

Вначале мы воспользовались традиционным для лесоводов и таксаторов способом определения нужных показателей на модельных деревьях, которых вначале было отобрано 40 шт. Их отбор проводился не в полевых, а в камеральных условиях, и удалось в полной мере выполнить главные условия их правильного выбора – случайность и репрезентативность. Для этого ведомость всех деревьев сортировали по возрастанию диаметров и выбирали модели через равные промежутки соответственно частотам диаметра (рис. 3).

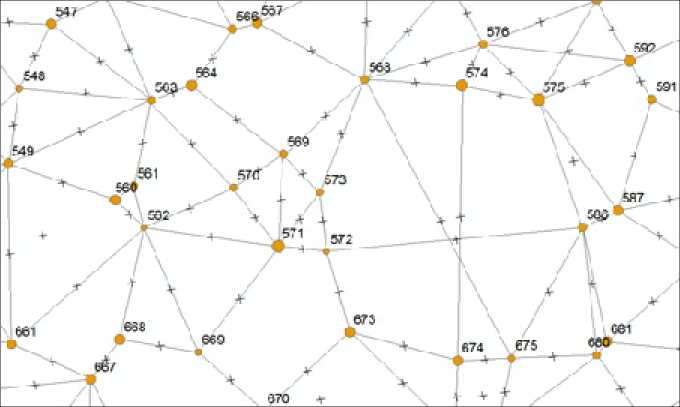
Рис. 1 . Соединение линиями 3–8 деревьев-„соседей“ и отметка на этих линиях середины расстояния между ними

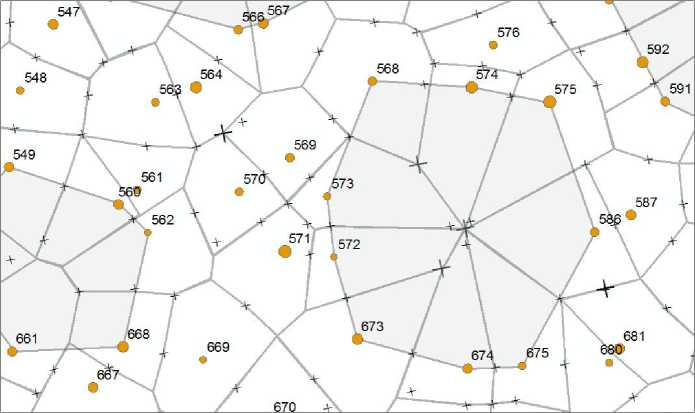
Рис. 2 . Выстраивание полигонов питания деревьев сосны в 184-летнем древостое. Пояснения в тексте

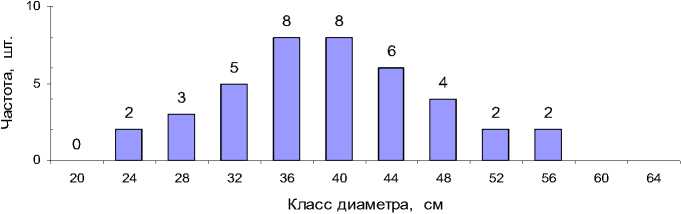
Рис. 3 . Репрезентативная выборка моделей по частотам классов диаметра

Камеральный способ выбора моделей позволил избежать предпочтений тем или иным деревьям, что неизбежно происходит при «полевом» способе, когда их осознанно выбирают часто вдали от окон и прогалин. В этой репрезентативной выборке среднее значение расстояния до 7–12 „соседей“ составило 720 см. Диаметры деревьев-моделей коррелировали здесь с расстоянием до окружающих их соседей с r = 0.167±0.150 (рис. 2).

Считая эти расстояния фактором, можно опре- делить силу его влияния по коэффициенту детерминации, который рассчитывают через квадрат корреляции, что определит его значение r2 = 0.1672 = 0.028 или 2.8%. Аппроксимация линейной связи здесь равна R2 = 0.008 (рис. 4), что также указывает на очень слабую силу влияния этого расстояния, равную 0.8%.

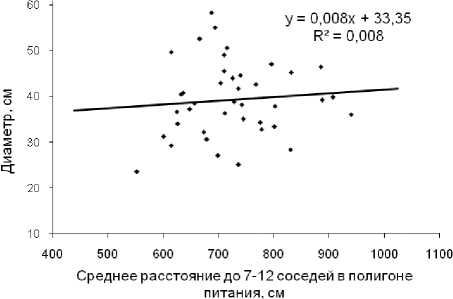
Рис. 4. Влияние среднего расстояния до „соседей“ на диаметр модельных деревьев сосны

Так как влияние оказалось очень слабым, то для более детального выяснения его значений число моделей увеличили до 55 шт., и в этой, уже увеличенной выборке, где малых и крупных моделей было больше, деревья разделили на три группы: отставшие в росте с диаметром 21–30 см (12 шт.), средние с диаметром 31–47 см (29 шт.) и крупные с диаметром 48–59 см (14 шт.). Оказалось, что среднее расстояние до „соседей“ в этих группах постепенно увеличивалось и составило 632, 708 и 755 см соответственно. Если соотнести квадраты указанных расстояний со средним расстоянием до соседствующих деревьев (720 см), то получим усиление взаимодействия с „соседями“ для отставших в росте деревьев в 7202 / 6322 = 1.3 раза, а для крупных ослабление взаимодействия до 7202 / 7552 = 0.91 раза. Однако, даже в этой увеличенной (и уже неслучайной) выборке, коэффициент корреляции повысился всего лишь до r = 0.26±0.13 при аппроксимации тренда связи R2 = 0.068, а влияние расстояния до „соседей“ на диаметр дерева оказалось по-прежнему слабым и равным всего лишь 6.8%.

Таким образом, среднее расстояние до 7–12 „соседей“ влияет на диаметр сосны в случайной репрезентативной выборке с силой всего лишь 2.8%, что позволяет отнести этот фактор к очень слабому, что явно противоречит парадигме конкуренции, где фактор расстояния до „соседей“ должен быть сильным.

Изучение полигонов питания

Построение полигонов для выбранных случай- но и репрезентативно 40 моделей показало, что доставшаяся дереву площадь питания повлияла на его диаметр в возрасте 184 года в очень слабой степени. Корреляция этих показателей оказалась равна r = 0.30±0.14 (коэффициент детерминации 9%), при аппроксимации тренда линейной связи R2 = 0.010, что дает оценку силы влияния площади питания на диаметр дерева на уровне всего 1.0%.

При выстраивании полигонов вокруг моделей сразу выяснилось, что для точной прокладки контура таких полигонов их нужно строить также и у 3–5 и более „соседей“ модельного дерева, особенно вблизи прогалин и в биогруппах. Поэтому далее мы выстроили полигоны питания уже для всех деревьев, исключая деревья по краям участка (рис. 5).

Всего удалось рассчитать площади питания у 323 деревьев из 375, при максимальном значении 79.9 м³ и минимальном – 7.9 м³. Средняя площадь питания оказалась равной 25.7 ± 0.58 м³ при вариации 40.9%. Исследование полигонов питания показало, что деревья использовали доставшиеся им индивидуальные площади питаний совершенно по-разному. Между площадью питания дерева и его диаметром корреляция оказалась равна r = 0.277±0.051, которая была достоверна (t факт =5.4 > t 0.99 = 2.6). Коэффициент детерминации на ее основе равен 0.077, что очень близко к значению аппроксимации линий регрессии линейной (R² = 0.076), степенной (R² = 0.075) и полиномиальной (R² = 0.078). Это дает достаточно надежную оценку силы влияния доставшейся дереву площади питания на его диаметр в 184 года, равную в среднем 7.7% (рис. 6).

Заметим, что при исключении из этой общей выборки лишь одного значения (точка в правом нижнем углу на поле диаграммы) связь поднималась до r = 0.303±0.051, а значения аппроксимации регрессии увеличились до 9.1%.

Как видим, даже «очистка» выборки от сильно уклоняющихся значений мало что изменила. Связь все равно осталась на очень слабом уровне, практически незначимом. Такая связь никак не может быть основанием для утверждения о том, что «чем больше дереву досталась площадь питания, тем крупнее оно сформировало по размерам ствол к возрасту спелости». Здесь имеется лишь тенденция. Аппроксимация линии тренда (R2 = 0.076) показывает, что лишь 7.6% изменчивости диаметра детерминировано доставшейся дереву площадью питания. В самом деле, разброс точек настолько велик, что при модальной площади питания 15– 35 м2 сформировались деревья как самые мелкие, так и самые крупные, с колебаниями диаметров от 21 до 59 см.

Выстраивание полигонов питания требует сложных интерполяций. Более простым выглядит замер расстояний до 7–12 соседей, поэтому интересна корреляция между средним расстоянием до них и площадью питания. Искомая корреляция, рассчитанная по модельным деревьям, оказалась среднего уровня (r = 0.57±0.11), а это значит, что замена площади питания связанной с ней характеристикой в виде расстояния до „соседей“ не вполне корректна.

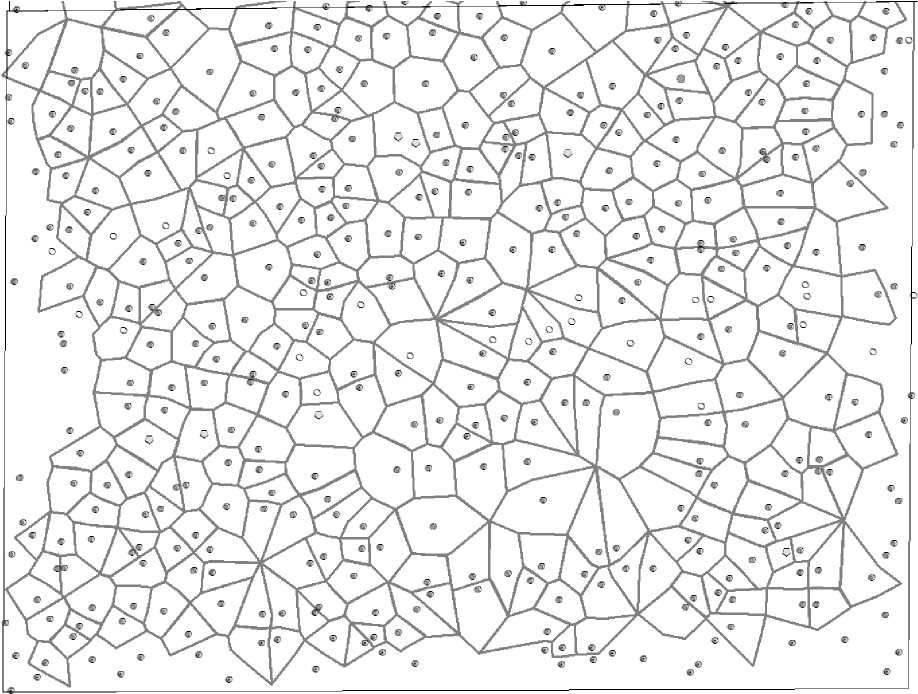
Рис. 5 . Полигоны питания деревьев сосны: темные точки – живые; овалы –деревья, вываленные ветром 14 лет назад и недавно отпавшие деревья на площади 1.094 га

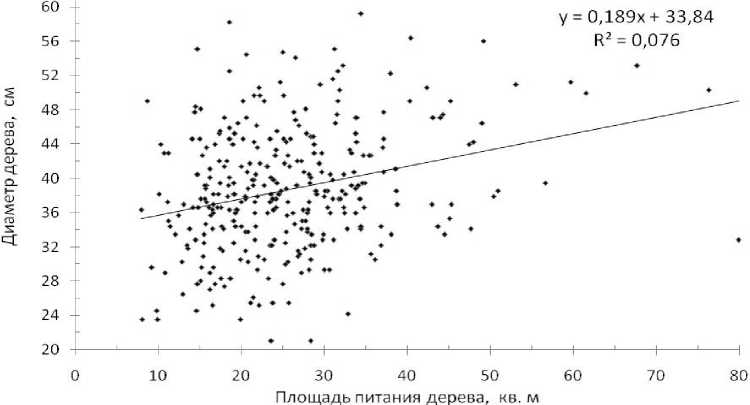
Рис. 6 . Влияние площади питания дерева на его диаметр

Так как в нашем распоряжении оказалась выборка из 323 деревьев, то мы разделили ее на две части: в первую часть отобрали деревья, площадь питания которых захватывала часть территории прогалин (125 шт.), а во вторую те, которые находились вдали от них, т.е., как бы суммировали микроценозы «редкие» и «густые». Оказалось, что средние диаметры в первой группе были несколько выше (40.1±0.7), чем во второй группе (37.8±0.5), и это было вполне ожидаемо. Неожиданным оказалось другое, а именно, деревья вблизи прогалин более активно воспользовались доставшейся им дополнительной площадью питания, и при ее средней величине 31.5±1.0 м3 она коррелировала с диаметром дерева при r = 0.400±0.075, тогда как без прогалин она оказалась равна 22.0±0.6 м3 и вообще не влияла на диаметр дерева, так как корреляция оказалась близка к нулю при r = 0.081±0.071. При этом вариация и пределы колебаний площади питания остались близкими, т.е., при отсутствии в структуре древостоя прогалин и более плотном стоянии деревьев, влияние доставшейся дереву площади питания на его размеры прекращается. И это опять-таки противоречит устоявшимся представлениям о том, что с увеличением густоты микроценозов деревья должны более активно использовать любое увеличение индивидуальной площади питания.

Обсуждение результатов

Размеры деревьев сосны оказались только на 7.6% обусловлены влиянием площади питания, а 92.4% изменчивости их размеров определяло влияние неизвестных и неучтенных факторов. Это намного ниже результатов других авторов при расчетах площади питания по полигонам, где при «полевом» способе отбора моделей (т.е. вдали от окон и прогалин) влияние площади питания достигло в среднем 27% [Нагимов, 2000]. Но это были не случайные, а типические выборки, и неслучайная методика их отбора вполне объясняет причину повышения влияния площади питания. Сравнивая собственные результаты с результатами у других авторов, З.Я. Нагимов признает, что и у них [Поляков, 1973; Мартынов, 1976; Тябера, 1982] были близкие результаты.

Все эти экспериментальные факты в целом лишают теоретических оснований давнее положение (точнее, предположение, а если еще точнее, то гипотезу) лесоводства о том, что при увеличении индивидуальной площади питания деревья должны увеличивать свои размеры, так как конкуренция ослабевает. Действительно, она становится меньше. Однако полученные результаты свидетельствуют, что таких деревьев, «правильно реагирующих» на увеличение личной площади питания, в возрасте спелости оказывается меньшинство. И в литературе есть сведения, подтверждающие отсутствие влияния расстояния до соседей на размер деревьев-лидеров.

Это обнаружилось в культурах сосны одинаковой густоты, но с разным индексом равномерности, при схемах посадки 2.2×2.2 м, 5.0×1.0 м, а также 1.5×1.5 м и 2.0×1.1 м. Оказалось, что сокращение шага посадки с 2.2 до 1.0 м, т. е. в 2.2 раза, достоверно не повлияло на размер 500 и 1000 самых крупных деревьев на 1 га в возрасте 35 лет [Плантационное…, 2007, с. 133–137].

По-видимому, здесь дело в том, что именно в возрасте 20–35 лет в большинстве древостоев высших классов бонитета разворачивается основная драма их развития с достижением максимума прироста, после которого он снижается и начинается фаза регресса в развитии древостоя как сообщества, и на этот тренд падения повлиять уже очень трудно [Рогозин, 2018а]. Однако здесь возникает парадокс – прирост фитоценоза падает, но его сохраняют крупные деревья, продолжающие развивать свои кроны. Лесовод стремится увеличить для них площади питания, удаляя соседей-конкурентов (и получить при этом деловую древесину). Казалось бы, после этого деревья должны увеличивать свои кроны и прирост более интенсивно, но в большинстве случаев этого не происходит, так как в 30–45 лет в полную силу проявляется закон морфогенеза древостоев Г.С. Разина с переходом их развития к регрессу, когда текущий прирост резко падает. Именно в это время срабатывает также и важнейший механизм гомеостаза популяции с изменением частот правых и левых форм, имеющих доказанные генетические отличия. Дело в том, что каждая популяция включает в себя субпопуляции-изомеры (правые и левые формы), а изменение их частот – необратимый процесс, и их частота сохраняется далее до возраста естественной спелости, обеспечивая устойчивость фитоценоза путем регуляции текущей густоты в этот критический период с помощью генетических механизмов и отмирания части этих форм, не имеющих адаптации к усилению конкуренции, в результате чего выживают особи партнерского типа. Этот процесс был объяснен на модельных примерах в культурах сосны и ели [Голиков, 2014; Рогозин, 2018а].

Однако, если использовать «пропорциональные» полигоны питания, (повторно отметим, что такие полигоны зависимы от размеров дерева), то мы получим площадь питания, которая будет давать предсказуемо более высокую связь с приростом и размером деревьев в центре таких полигонов. Они используются в способах Штера, угловых проб и их модификаций с учетом размеров крон и коэффициентов конкурентного давления [Нагимов, 2000; Вайс, 2014], а также в исследованиях с использованием так называемых «областей доминирования» [Борисов и др., 2014; Иванов и др., 2017]. На наш взгляд, необходимо весьма критично отнестись к таким полигонам, так как они дают зависимые переменные и не могут выступать в качестве факторов.

Влияние доставшейся дереву индивидуальной площади питания на его диаметр оказалось у нас почти в 8 раз слабее, чем это получалось у ряда авторов при расчетах площади питания по пропорциональным полигонам, т. е. при ее расчете по зависимым переменным величинам. Так, расчеты по нескольким корреляционным отношениям по данным из обширного исследования З.Я. Нагимова [2000] показали, что пропорциональная площадь питания действует там на размер дерева с силой в среднем 59%. Однако в нашей последней работе [Рогозин, 2018б] мы показали, что ее применение в качестве фактора некорректно. Доверяя авторитетам, еще совсем недавно мы ошибочно считали ее фактором, действующим с силой 59% [Рогозин, 2018а], так как это хорошо согласовывалось с представлениями о древостое как сообществе растений, объединенных борьбой за существование [Сукачев, 1953], где конкуренция играет главную роль и где влияние площади питания должно быть сильным. Эта идеологема, что называется, застилала глаза и мешала разглядеть нестыковки давней теории естественного отбора с ее «борьбой за существование» с многообразием реальных взаимодействий деревьев. В насаждениях конкуренция является всего лишь одним из типов взаимодействий – наряду с толерантностью и партнерством деревьев, которые проявляют себя, например, разнесением во времени на 1–2 недели пика прироста у деревьев при их близком расположении, что было зафиксировано в биогруппах в девственных елово-пихтовых лесах Урала [Горячев, 1999].

Поэтому для проверки наших подозрений о резком повышении влияния пропорциональных полигонов питания на размер дерева, мы специально рассчитали также расстояния между центральным деревом и его 7–12 „соседями“ с делением расстояния к ним на две части пропорционально их диаметрам. В результате получили «пропорциональные» расстояния до „соседей“. Вполне ожидаемо связь между средним «пропорциональным» расстоянием до них и диаметром дерева сразу возросла до r = 0.60±0.09 при аппроксимации тренда связи R2 = 0.364, а в увеличенной выборке из 55 моделей она повысилась вообще до r = 0.71±0.07. И это увеличение было вызвано не повышением силы «влияния» расстояний, а расчетом этих расстояний так, что в них уже было влияние размера дерева на это расстояние (бóльшую половину расстояния приписывали крупному, а меньшую – мелкому дереву). Естественно, корреляции резко возросли, и была получена оценка «силы влияния» в 36.4% (по R2 = 0.364), которая сразу увеличилась на порядок в сравнении с влиянием независимой переменной (простого среднего расстояния до „соседей“), где ее влияние было всего лишь 2.8%.

Вполне очевидно, что далее и пропорциональная площадь питания, как зависимая переменная, также будет образовывать более высокую связь с диаметром дерева. И проверка ее повышения не нуждается в дополнительных расчетах, которые достаточно сложны, так как использование пропорциональных полигонов в качестве «фактора», влияющего на прирост и на размер дерева, происходит по недоразумению, допущенному в самом начале их применения в 1970-е гг. [Assmann, 1961; Поляков, 1973; Тябера, 176]. В таких полигонах уже есть влияние размера дерева, так как большая часть площади приписывается крупному, а меньшая – мелкому дереву.

Анализ темы конкуренции деревьев в работах отечественных и зарубежных исследователей в историческом аспекте показал [Усольцев и др., 2018], что указанное «недоразумение» с пропорциональной площадью питания и ее широким применением [Вороной, 1952; Тябера, 1982; Нагимов, 2000; Грабарник, 2010; Борисов и др., 2014] получилось неслучайно. Дело в том, что с конца XIX в. в биологии начала доминировать теория отбора Ч. Дарвина с его борьбой за существование и выживанием сильнейших особей, и буквально единичные работы были посвящены теме кооперации и партнерства. Дарвинизм и поныне является «…отправной точкой любого биологического исследования по умолчанию» (Усольцев и др., 2018, с. 234). Грубая модель эволюции Ч. Дарвина была навязана всему миру его воинствующими последователями-атеистами, преследовавшими политические цели (Баландин, 2010). Множество противоречащих дарвинизму работ более 100 лет не включались в парадигму биологии вплоть до XXI в., начиная с работ выдающихся ученых К.Ф. Кесслера, В.М. Бехтерева, В.В. Докучаева. Они полагали, что «…организация сообществ построена на единстве процессов конкуренции и кооперации как в животном, так и в растительном мирах. При этом закон взаимной помощи в прогрессивной эволюции играет гораздо более важную роль, чем закон взаимной борьбы» [Усольцев и др., 2018, с. 236].

Недавно появились работы [Демаков и др., 2011; Демаков, 2018], где многомерный пространственный анализ с подробным картированием деревьев показал, что их размеры зависят в большей степени не от внутривидовой конкуренции, а от экологической неоднородности биотопа и наличия в нем благоприятных и неблагоприятных зон. Еще в одной из работ изучение микроценозов в 80–150летних смешанных древостоях с высокой полнотой, состоящих из шести пород, показало [Шанин, 2015], что деревья освоили большинство учетных площадок размером 5×5 м очень слабо, так как полнота и густота их оказалась низкой, а диаметр деревьев небольшим. Число же площадок с очень высокой полнотой составило всего 1.6–3.7%. Деревья на них оказались очень крупными, при этом также и число деревьев на них было выше среднего уровня. Данный феномен авторы [Демаков и др., 2011] предложили доказывать в дальнейших исследованиях с трех позиций: наличием в биотопе особо благоприятных зон для роста деревьев; наследственными свойствами особей; проявлением принципа агрегации особей Олли, т.е. эффектом группы [Alle, 1931, 1938; Одум, 1975; Марченко, 1995].

Современные методы пространственного анализа, в частности, работа со слоями карт в программе ArcMap, позволили нам получить новые данные, подтверждающие полученное ранее резкое снижение конкуренции между деревьями в спелом возрасте [Рогозин, 2018в, г]. Данные эти чрезвычайно важны. Они позволяют утверждать, что фенотип дерева в древостое определяют отнюдь не конкуренты-„соседи“, которые ограничивают ресурсы питания и влияют на размер индивидуальной площади питания дерева в микроценозе, а иные факторы, которые нам пока неизвестны или трудноопределимы.

Заключение

Итак, репрезентативная выборка моделей позволила установить, что индивидуальная площадь питания дерева достоверно коррелирует с его диаметром при r = 0.277±0.051, что характеризует силу влияния этого фактора как слабую. По коэффициенту аппроксимации тренда этой связи сила этого влияния составляет 7.6%. Более сильным фактором, по литературным данным, можно считать влияние генотипа дерева, действующего с силой около 30%. Вследствие этого можно утверждать, что индивидуальный размер дерева в насаждении определяет, в первую очередь, генотип дерева, действующий в 4 раза сильнее, чем доставшаяся дереву площадь питания. В сумме эти два фактора определяют размер дерева на 40%. В итоге получается, что нам неизвестна большая часть (60%) факторов, определяющих размеры деревьев в древостое. Поэтому в практическом плане рубки ухода в среднем и приспевающем возрасте (прореживания, проходные рубки), которые увеличивают индивидуальные площади питания деревьев, теоретически могут повлиять на размер деревьев к возрасту спелости с силой менее 10%. Во много раз сильнее повлияет генотип, проявления которого опознаются по деревьям-лидерам и которые следует сохранять даже при самых малых расстояниях между ними (в биогруппах). Именно на этот генетический фактор и должны быть направлены уси- лия лесоводов, обеспечивающие крупным деревьям комфортные условия с самого раннего возраста, с проведением активной регуляции общей густоты фитоценоза, которая действует на размеры всех деревьев насаждения с силой около 90%. Регуляцию следует заканчивать задолго до наступления максимума прироста, т. е. в возрасте 10–15 лет, а далее проводить уход по низовому способу.

Полученные результаты весьма серьезны – они меняют наше общее представление о силе влияния расстояний между деревьями и площадями их питания на их продукционные показатели. Прежде они считались сильными факторами априорно, а теперь, по результатам наших исследований в старых насаждениях сосны, будут отнесены к факторам, слабо влияющим на размер соседствующих деревьев. И это слабое влияние регистрируется здесь как результат всего предшествующего развития деревьев в насаждении. При этом остаются невыясненными их численные значения в прошлом. Поэтому для выяснения их влияния в динамике нужны дальнейшие исследования на репрезентативных выборках в более молодых (средневозрастных и приспевающих) насаждениях.