Плотность дисперсно-наполненных композитов

В статье приводятся методы определения плотности, их анализ, сравнение расчетных значений с экспериментальными. Рассматривается связь плотности с состоянием структуры полимерного композиционного материала. Даются рекомендации по использованию методик измерения плотности композитов и его компонентов для осуществления оптимизации составов.

Плотность непосредственно связана как с состоянием структуры композитного материала (КМ) в целом, так и с состоянием его отдельных компонентов и является важным показателем. Известно, что граничные слои матрицы у поверхности частиц наполнителя обладают более высокой структурированностью, чем матрица в массиве. Это приводит к существенным изменениям в строении матрицы и оказывает непосредственное влияние на ее плотность. Кроме того, в КМ в той или иной мере развиваются процессы порообразования, влияющие в первую очередь на плотность материала.

Наиболее простым методом плотность КМ определяется в соответствии с правилом смеси, являющимся по существу соотношением аддитивности:

РС1= Рги + Рр О ~ иХ <0’65 ^ и ^ °>4), (D где рс, pf и рр— плотности композита, наполнителя и ненаполненной матрицы соответственно. Такая зависимость дает приемлемую оценку плотности лишь в середине интервала наполнения (0,65 > и > 0,4).

При малом и большом содержании наполнителя проявляются краевые несоответствия, обусловленные преимущественным влиянием одной из фаз. Действительно, при малом содержании наполнителя (0,4>и>0) плотность КМ в основном зависит от плотности матрицы, тогда как при высоких степенях наполнения (0,87>и>0,6) она определяется преимущественно плотностью наполнителя.

Для малонаполненных композитов с минеральными наполнителями принимается гипотеза, что относительное уплотнение композита пропорционально объемному содержанию наполнителя:

Д pc/pp = (pc-pp)/pp=v.

Данное соотношение приводит к простой зависимости:

рс2 = Рр (1 + и), (0,4 > о > 0),        (2)

особенностью которой является отсутствие величины плотности наполнителя.

Произведем анализ второго краевого решения, характерного для высоконаполненных композитов. Высокое наполнение обеспечивается полидисперсным наполнителем, для которого плотность упаковки соответствует величине д-0,868. В этой связи принимается гипотеза, согласно которой плотность КМ в первом приближении не должна превышать Рс~ Л Pf = 0*868 рг Иначе это выражение записывается в виде

Pc-Pf(i~^), где д = 0,868, а = 8,7. Если плотность упаковки наполнителя не достигает предельной величины (д - 0,868) и находится в интервале значений 0,87 > v > 0,65, характерном для высоко-наполненных КМ, приведенная зависимость принимает более общую форму:

Р_ЕЗ = Р_Г(1- а), (0,87 > v > 0,6),      (3)

где а — постоянная величина. Отметим, что формула (3) справедлива при о >0,1.

В аддитивном равенстве (1) не учтено то обстоятельство, что часть объема матрицы переходит в состояние уплотненных граничных слоев. Оценка усредненного значения уплотнения матрицы показала (табл.), что эффект уплотнения может достигать 7 %. Эго незначительно отличается от интервала уплотнения (3^6) %, установленного Ю. С. Липатовым [1]. Для численных оценок можно принять величину уплотнения, равную ~3%, тогда Р| ~ ~ 1,03 рр. Объемная доля граничных слоев определяется из выражения vt = 0,48 и. Тогда плотность КМ можно определить по уравнению

P^PfV + PpU-v-vJ + p.v,.

Несложные преобразования полученного равенства с учетом вычисленных значений р( и и, позволяют получить расчетную зависимость:

Р^ = РС1 + 1,44 • 103 р о, (0,87 > v > 0,4), (4) где р{] — плотность КМ по уравнению (1).

Экспериментальные исследования плотности производились на трех сериях образцов из эпоксидных (серия 1 и 3) и полиэфирных (серия 2) композитов (см. табл.). В качестве наполнителей использовались молотый кварц (серия 1), молотый кварцевый песок (серия 2) и молотая слюда (серия 3). Вследствие анизометрии отдельных частичек слюды, имеющих пластинчатую форму, высокого наполнения эпоксидной смолы в образцах третьей серии достигнуть не удалось. Объемное содержание наполнителя изменялось в интервале 0,71 >u>0. С целью отличия расчетных значений плотности КМ по приведенным формулам использованы порядковые индексы рс1, рй, Рс3,Рс4.

Сравнительный анализ показал, что расчетные зависимости (1), (2), (3), (4) могут использоваться в соответствующих интервалах содержания наполнителя для прогнозирования плотности дисперсно-наполненных композитов с минеральными наполнителями.

Измерение плотности ненаполненной матрицы рр осуществляется технически несложно. В свою очередь плотность матрицы в композите рт можно оценить лишь приблизительно. Поскольку композит является

Таблица

Сравнение экспериментальных (р) и расчетных (р^ р_е2 р, р_с4) значений плотности исследованных композитов

	рс10"3, кг/м3	Рс1ЮЛ кг/м3	рс30-3, кг/м3	Р/ЮЛ кг/м3	кг/м3	р-10"3, кг/м3
Серия 1 (pf = 2,5-103, кг/м1)
0	1,22	1,22	1,22		1,22	1,22
0,29	1,57	1,59	1,57		1,60	1,07
0,45	1,77	1,78	1,77		1,79	1,10
0,55	1,94	1,92			1,94	1,28
0,62	2,04	2,01		2,04	2,03	1,31
0,67	2,11	2,08		2,07	2,10	1,32
0,71	2,15	2,13		2,10	2,15	1,28
Серия 2 (pf = 2,56-103, кг/м3)
0	1,24	1,24	1,24		1,24	1,240
0,31	1,64	1,65	1,63		1,66	1,180
0,48	1,91	1,87	1,84		1,89	1,397
0,58	2,02	2,00		2,05	2,02	1,290
0,65	2,1	2,10		2,10	2,12	1,250
Серия 3 (pf = 2,6-103, кг/м3)
0	1,17	1,17	1,17		1,17
0,037	1,19	1,22	1,21		1,22
0,088	1,25	1,30	1,27		1,30
0,162	1,32	1,40	1,36		1,40
0,278	1,52	1,57	1,5		1,57

многокомпонентной системой, в которой ее составляющие связаны в единую структуру, то выделение из общих свойств КМ какого-либо свойства одного из компонентов (в данном случае р„) не всегда представляется возможным. Замена рт на рр неадекватна, поскольку при наполнении композита матрица трансформируется в пленочное состояние, отличающееся от ненаполненного полимера.

Обычно для определения плотности матрицы используется экспериментально-расчетный метод. Ввиду того что жесткие частицы неорганических материалов не претерпевают каких-либо изменений в структуре композита, их плотность считается неизменной. Далее измеряется плотность композита ре и расчетным путем находится рт. Представим формулу для расчета в общем виде:

Р^Р^ + Р^О-^-^ + Мы <5> где pf и рь— плотность соответственно наполнителя и воздуха; иь — объемная доля воздушных включений в композите. Согласно выражению (17), плотность матрицы в композите составляет:

Рт = (pr- Pf» - РьЧ)z о - V - »ь) (6)

Для расчета рш необходимо знание всех величин, входящих в правую часть равенства. Значения рс, pf и рь определяются экспериментально. При этом плотность воздуха заведомо известна и составляет ph = 1,3 кг/м3.

Если композит содержит большое количество изолированных пор, то объем воздуха иь невозможно установить опытным путем. В этом случае воздушные включения устраняются. Образцы композита измельчаются до такой степени, чтобы в отдельных частичках композитного порошка не оставалось пор, после чего определяется плотность полученного порошка. Считается, что таким образом получается плотность композита без пор. Однако при измельчении нарушается пленочная структура матрицы, разрушаются адгезионные слои. Все это приводит к тому, что измельченная матрица теряет присущие ей специфические свойства, что вносит погрешность в вычисление рт.

Эффект уплотнения матрицы в композите можно установить в результате косвенного, сравнительного расчета. Обозначим плотность матрицы с воздушными включениями ртЬ. Тогда формула (5) приобретает вид:

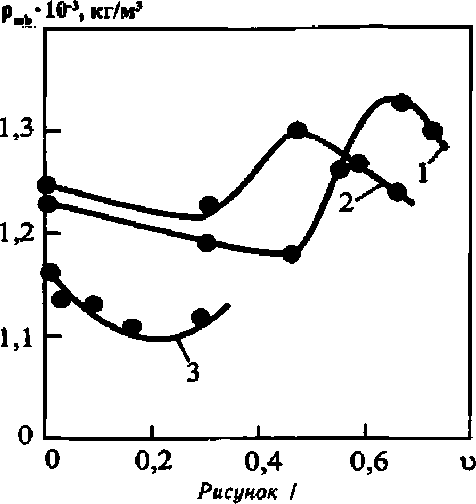
Зависимость плотности матрицы от объемного содержания наполнителя: 1, 2, 3 — КМ соответственно 1, 2 и 3-й серий (см. табл.)

P^P^ + P^U-V)- ^

Здесь предполагается, что частицы наполнителя пор не имеют. Из формулы (7) несложно рассчитать р^, предварительно определив Pf и и.

Расчеты показали, что плотность р^ претерпевает экстремальное изменение при и = =0,5. Для эпоксидного композита, наполненного молотой слюдой, такого наполнения достигнуть не удалось из-за высокой дисперсности и анизометрии отдельных частичек слюды.

Уплотнение матрицы по сравнению с нена-полненным полимером (о = 0) в среднем составило 6 %. Возможно, происходит снижение пористости при наполнении композита, тогда окажется, что эффект уплотнения матрицы является артефактом. В то же время микроскопические исследования показывают, что с увеличением степени наполнения пористость КМ возрастает.

Обсудим вопрос о пористости матрицы более детально. Рассмотрим, например, полиэфирный композит, у которого эффект уплотнения матрицы наиболее выражен при и =0,48. Подставив табличные данные pf и рс, соответствующие и=0,48, в формулу (3), получим рпА = 1,31 КУкг/м3. Для ненаполненной полиэфирной смолы с воздушными включениями имеем р^ = 1,24 Ю^г/м3 (см. табл.). Складывается впечатление, что по- ристость матрицы при и = 0,48 меньше, чем у ненаполненной смолы. В связи с этим произведем сравнительные расчеты. Примем р^ за точку отсчета и предположим, что истинная плотность матрицы в композите рга соответствует этому значению.

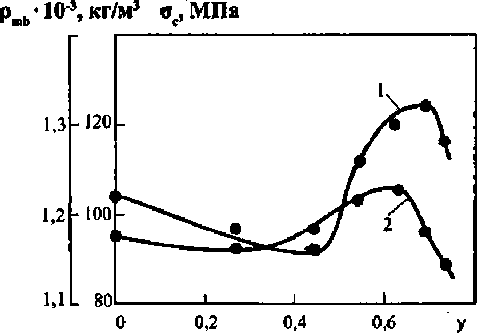
Рисунок 2

Зависимость плотности матрицы (1) и прочности при сжатии (2) эпоксидного композита от объемного содержания молотого кварца (Su= 100 мг/кг). Серия 1

Отсюда по формулам (5) и (7) находим:

РшьО-^Р^О-^Ч^РьЧ- ^

Учитывая, что для композита v = 0,48, на ходим оь = -0,029. Величина характеризует уменьшение (знак «минус» перед иь) величины р^ в сравнении с р^, что равносильно снижению объемной доли пор у матрицы на 0,029. Не следует, однако, полагать, что так и происходит в действительности, просто в данном случае иь служит оценочным эквивалентом. Запишем р^ в виде

Ррь^РрО-^ + РьЧ- ^ где рр — плотность ненаполненной смолы без воздушных включений.

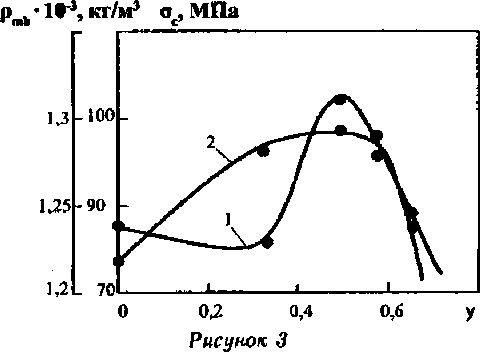
Зависимость плотности матрицы (1) и прочности при сжатии (2) полиэфирного композита от объемного содержания молотого кварцевого песка (Se = 150 м1/кг). Серия 2

Из формулы (9) определим, какой должна быть рр при снижении пористости смолы на иь =0,029. Если окажется, что она совпадает с pinb, то уплотнения не существует. Расчет показал, что рр = 1,28 103 кг/м3 Следовательно, если даже пустотность ненаполненной смолы уменьшается на vh = 0,029, то плотность ее не достигает значения р^ = 1,31 - 103 кг/м3.

Таким образом, эффект уплотнения Др = = pmb-ррь™ 30 кг/м3 наблюдается и в этом случае. Истинного значения ртсравнительный расчет не выявил, поскольку неизвестна точная доля пор оь. Можно лишь отметить, что оно было бы выше величины ршЬ= 1,31 103 кг/м3

На рис. 2—4 приведены зависимости плотности р^, прочности при сжатии о. и предела текучести ат от содержания наполнителя в композитах первой и второй серий. Видно, что между кривыми pmb = f (и) и о. = f (v) прослеживается корреляция (см. рис. 2, 3). Видимо, в ее основе заложен механизм перехода квазижидкостной фазы КМ в кв азитвердотельную.

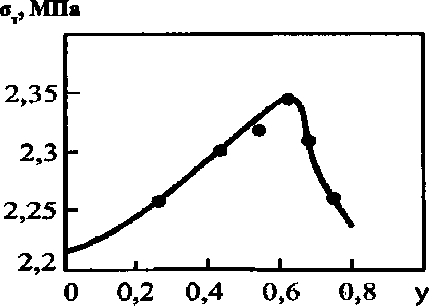
Рисунок 4

Зависимость предела текучести эпоксидного композита, наполненного молотым кварцем, от объемного содержания наполнителя.

Серия 1

Интерпретация уплотнения матрицы заключается в следующем. При относительном смещении частиц наполнителя в процессе совмещения компонентов композита на полимерную матрицу действуют значительные сдвиговые напряжения, приводящие к снижению конформационной подвижности макромолекул, а следовательно, к проявлению эффекта ориентирования в пленочной фазе матрицы.

Такой процесс можно грубо уподобить упрочняющей ориентационной вытяжке полимера. О снижении подвижности цепочек макромолекул полимерной матрицы свидетельствует хрупкий характер разрушения высоконапол-_№^^«„™_т< т. пх;лпшл липшидл i ud >  х^ t cpniccлпс з^д^слия п сдвиговые напряжения создают в структуре матрицы условия, приводящие к сближению линейно-ориентированных макромолекул. В результате наблюдается общее повышение ее плотности. Уменьшение р^ при малых о (см. рис. 1) связано с нарушением регулярности структуры матрицы в массиве отдельными

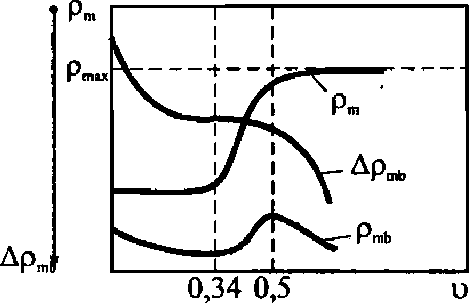
Рисунок 5

Зависимость плотности полимерной матрицы в композите от объемного содержания наполнителя частицами наполнителя, приводящим к ее разрыхлению и порообразованию. В высоконапол-ненных КМ (у > 0,5) происходит интенсификация порообразования вследствие дробления пленочной матрицы. Становится ясным, что увеличение плотности матрицы ртс ее переходом в пленочное состояние и разуплотнение за счет воздушных включений (-Др^) есть два конкурирующих фактора.

На рис. 5 представлены функции -Др = = f (и) и pm = f (у). Их сумма дает результирующую кривую;

^mb ^^ = Рщ (^) ~ ^^mb (^)* <10>

С повышением и порообразование (и его эквивалент |АртЬ|) непрерывно увеличивается. В свою очередь рт практически не меняется до наполнения у = 0,34. При и > 0,34 вследствие образования перколяционного каркаса из пленочной матрицы и его развития рт нарастает по затухающей кривой до значения pmii, характеризующего предельно устойчивую пленку матрицы.

Здесь величина р_т берется средней по объему композита. Тот факт, что р_т не меняется в интервале и = ((Н0,34), не говорит о том, что в отдельных микрообъемах КМ локальная плотность матрицы постоянна. жл nviev 1срлил иира^исапллл vna j me при. и < 0,34 начинает расти.

Поскольку при наполнении КМ происходит последовательный переход матрицы из состояния массива в состояние уплотненных граничных слоев, формирующих пленочную фазу матрицы, возникает непосредственный интерес в нахождении плотности матрицы (pt) в граничных слоях. По результатам оценки плотности матрицы (р^) с воздушными включениями можно заранее предположить, что pt в процессе наполнения композита будет так же, как и р^, изменяться экстремально — от возрастания к снижению.

Для нахождения расчетной зависимости используем гипотезу, согласно которой объем матрицы с плотностью рт поделен между фазой матрицы в массиве и плотностью рр, соответствующей плотности ненаполненно-го полимера, и пленочной фазой матрицы с плотностью ре, сформированной из граничных слоев полимера. Принимая это во внимание и используя правило смеси, имеем

P_t = Рг» + Р_ьи_ь ^ Р, v, + р₀ (I - и - v_b- у,), (И) где у₍ — объемная доля пленочной матрицы в композите, р₀ — плотность матрицы в состоянии массива. Искомая величина р, находится из выражения

Р. = [ре - Pf° - Ръиь - Ро (1 - У - vt" V)] / и,. (12) Приведенное равенство имеет три неизвестных: р0, у( и иь. В первом приближении можно принять, что плотность матрицы в массиве совпадает по величине с плотностью ненаполнен-ного полимера р0 = р., и тем самым сократить число неизвестных. Здесь представляется возможным независимо установить лишь и^ тогда как значение иь из простых соображений не определяется. В данном случае зависимость (12) можно использовать в расчетах, если пренебречь воздушными включениями. Таким образом, пористость будет учтена в искомой величине р, и тем самым будет занижать ее значение. Тем не менее, если окажется, что pt> рр для каких-либо определенных значений содержания наполнителя у, то это будет подтверждением предположения об уплотнении матрицы в граничном слое. Исключая неза- висимое влияние пористости, получим более простое выражение:

p. = [pc-pf»-pp(l-v-yl)]/yl-

Принимая во внимание соотношение (4.15), определим окончательную расчетную зависимость:

р, = [рс - prv - рр (1 - 1,48v)J / 0,48v.    (13)

В табл, представлены результаты расчета pt для первой и второй серии образцов.

Анализ показывает, что плотность граничных слоев полимерной матрицы pt изменяется нерегулярно с ростом объемного содержания наполнителя, а зависимость pt = f(u) имеет сложную S-образную форму с двумя экстремумами (см. табл.). Причем при значениях содержания наполнителя и, соответствующих экстремуму-максимуму, наблюдается превы шение плотности матрицы в граничных слоях в сравнении с ненаполненным полимером в среднем составившее 10 %.

Следует отметить, что положение экстремума-максимума на оси и полностью соответствует положению экстремума-максимума графической зависимости изменения прочности от объемного содержания наполнителя (см. рис. 2 и 3), который отвечает оптимальной структуре композита и отражается рецептурным показателем оптимального объемного содержания (ив)наполнителя. Поэтому представляется весьма целесообразным производить поиск оптимального рецептурного решения по нетрудоемкой методике измерения плотности композита и его отдельных компонентов.