Плотность спинового углового момента в остром фокусе светового поля с фазовой и поляризационной сингулярностями

В параксиальных световых полях плотность спинового углового момента (СУМ) рассматривается как скалярная величина, так как поперечные компоненты вектора СУМ пренебрежимо малы. В условиях острой фокусировки поперечный СУМ может давать существенный вклад, что приводит к такому физическому эффекту, как фотонное колесо [1]. Если же СУМ имеет только продольную компоненту (хотя в пучке до фокусировки она была равна нулю), возникает эффект продольной магнетизации [2]. Наряду с волнами, распространяющимися в пространстве, поперечный СУМ исследовался в затухающих волнах [3], а также в диэлектрических и металлических волноводах [4]. В работе [5] СУМ измерялся экспериментально, а в [6, 7] изучалось воздействие спина светового поля на микрообъекты. В остром фокусе СУМ исследовался для Гауссовых пучков [8] и для оптических вихрей [9]. В [10] рассматривалась острая фокусировка оптических вихрей с поляризационной сингулярностью, однако исследовался только орбитальный угловой момент, но не спиновый. В данной работе получены аналитические выражения для компонент вектора плотности СУМ оптического вихря с поляризационной сингулярностью, включая радиальную, азимутальную и седловую поляризацию. На примере узкого кольцевого пучка показано наличие в фокальной плоскости областей с полностью продольным СУМ для азимутальной поляризации, полностью поперечным СУМ для седловой поляризации и приближённо поперечным для радиальной.

• 1.    Общие выражения для плотности СУМ в остром фокусе светового поля

с поляризационной и фазовой сингулярностью

В [11] получены формулы для декартовых компонент вектора электрической напряжённости светового поля в окрестности острого фокуса апланатической системы. Если в начальной плоскости имеется линейно поляризованный (вдоль оси x ) оптический вихрь с комплексной амплитудой A ( 9 )exp( in ф ), где n - топологический заряд вихря, A ( 9 ) - функция радиальной аподизации фокусируемого излучения, то вблизи фокуса комплексная амплитуда в цилиндрических координатах ( r , ф , z ) равна [10, 12]:

i n - 1

E x ( r , ф , z ) = — e i" ^ф ( 2 1 о, „ + e1 2, n + 2 + e1 2, n - 2 ) ,

E y ( r , ф , z ) = i—e " ^ф ( - e 2 1 2, „ + 2 + e 2 1 2, „ - 2 ) ,

Ez (r, Ф, z) = -ineinф (e»11,„ +1 - e-iф11,„-1), где функции Ip,n имеют вид (p =0, 1, 2):

Ip, n = kfJ sin 9 Vcos9 sinp (9/ 2) cos2-p (9/ 2)x

XA(9)e-kzcos9 J (^)d9,

где ^ = kr sin 9 , а определяет апертуру фокусировки, а 9 - угол с оптической осью, задающий положение точки на сходящемся сферическом волновом фронте.

Основываясь на (1) и (2), рассмотрим далее световое поле следующего вида:

E = A ( 9 ) e ™ ^ф

a 1 x e im ^ф + a _{2 x}e ^{- im ф} a 1 _ye^{im ф} + a ₂ y e ^{- im ф}

где n и m - целые числа, a 1 x , a 1 y , a 2 x и a 2 y - комплексные числа. Выражение (3) описывает световые поля с фазовыми и поляризационными сингулярностями. При m = 0 поле (3) является эллиптически поляризо

2. Плотность СУМ в остром фокусе оптического вихря с азимутальной поляризацией

ванным оптическим вихрем с топологическим зарядом n . При m = 1, a i x = a 2 x =1/2, a 1 y = - i /2 и a 2 y = i /2 поле (3) имеет радиальную поляризацию (если при этом m >1, то поле является поляризационным вихрем [13]). При m = 1, a 1 x = i /2, a 2 x = - i /2, a 1 y = a 2 y =1/2 поле (3) имеет азимутальную поляризацию. Если m = 1, a 1 x = a 2 x =1/2, a 1 y = i /2 и a 2 y = - i /2, поле (3) имеет седловую поляризацию. В теории векторных полей такие сингулярности известны как источник / сток, циркуляция и седло [14] (рис. 1).

\\\\f///Z   Zz.------ Z/MWWX

XXX \ \ f Z ZZ /Z,----/// / | \ \\\

^sxi/гх^              Z-ZZIIWX-^

Z / Z ! I \ X \ X        " ~" / / / X X X \ f / / / Z

а)                     б)                    в)

Рис. 1. Виды векторых сингулярностей: источник/сток (а), циркуляция (б), седло (в)

Плотность СУМ светового поля (с точностью до постоянного множителя) находится по формуле [3, 9]:

s = 4 Im ( E * х E ) .

Подставив (3) в (4), получим составляющие ности СУМ в цилиндрических координатах:

s z = Re { [ R 1 e^{-im ф} + ( - 1) ^mR ₂ e^{im ф}] * х

х[91 e -im ф + (-1)m 92 e™ф]}, sr =-2Im {[91 e-im ф + (-1) meim ф92 ]х х [Z 1 eimф + (-1)me-imфZ2]}, s ф = 2Re{[R1 e -im ф + (-1) meim ф R 2 ]х х [Z 1 eimф + (-1)me-imфZ2]},

плот-

где

Rp ( r, ф) = уp+e 1 ф( I0,n_(_1)pm + I2, n _(_1)pm+2 ) + \(8)

^+у p ^- e ф ( I 0, n - ( - 1 ) p m ⁺ I 2, n - ( - 1 ) p m - 2 ) ,

• ⁹ p ⁽ r , ф ) = У p + e^-iф ( I * n - ( - 1 )    ^- I 2, n - ( - 1 ) + 2 ) ^-

• \(9)

• -у* ^ф I *      „ -1 *

^{p (} 0, n - ( - 1 ) p m      2, n - ( - 1 ) p m - 2 )

Zp (r, ф) =

= v , e1 фТ      „    — y e 1 ф у P + e    1,n-(-1)pm+1    у p-e     1,n-(-1)pm-1,

где p =1,2, g p ± = ( a px т ia py )/2.

Выражения (5)-(10) являются общими для полей вида (3). Далее рассмотрим частные случаи.

В случае азимутальной поляризации у ₁₊ = Y 2- =0, у _1-= i /2, у ₂₊ = - i /2. Поэтому

s z

1 2              2

4 (| I 0, n - m|     |I 0, n + m | ⁺ | I 2

2, n + m - 2 |      |I 2

2, n - m + 2

+

- 1 ^m .

+ 2___ L_ P p j P ^-2 i ( ^{m -1} )ф *

+ 2 ^Re { ^e         ( I 0, n + m I 2, n - m + 2

*

² 2, n + m - 2-^0, n - m

При m = 1 плотность СУМ не зависит от угла ф :

s z = ~ ( ¹ 0, n - 1 ^{+ 1} 2, n - 1    ^{- 1} 0, n + 1 ^{+ 1} 2, n + 1

1² ) ■

Например, если фокусируется узкий кольцевой

пучок ( A ( 9 ) = 5 ( 9 - 9 a )), то

s z

kL Y 2 J

sin² 9 ₀ cos 9 ₀ х

х [ J 2 - 1 ( kr sin 9 ₀ ) - J_n n _{+ 1} ( kr sin 9 ₀ ) ] .

Из (13) следует, что продольная составляющая СУМ меняет знак на кольцах с радиусами

r p =у n , p /( k sin 9 0 ) , r ‘ =у П , p /( k sin 9 0 ) ,          (14)

где у _n , _p и у '_n , _p - соответственно p -й нуль функции Бесселя n -го порядка и её производной. Из неравенств для нулей функции Бесселя следует, что в центральной области ( r < r' 1 ) фокальной плоскости и внутри колец r_p < r < r'_p ( p =1,2,...) поляризация правая круговая, а в кольцах r'_p <  r <  r p она левая круговая.

Для поперечных компонент общие выражения громоздки, но из них для случая m = 1 следует, что обе они равны нулю: s_r = s _Ф = 0, то есть в случае азимутальной поляризации вектор плотности СУМ имеет только продольную составляющую. В таком фокусе можно реализовать 100% магнетизацию материала за счёт обратного эффекта Фарадея [2].

3. Плотность СУМ в остром фокусе оптического вихря с радиальной поляризацией

В случае радиальной поляризации у ₁₊ = у _2- = 0, у _1- = у ₂₊=1/2. Выражение для продольной составляющей СУМ отличается от выражения для азимутальной поляризации только знаком второго слагаемого:

s

= 4 (1 1 0. n - m |² -| 1 0, n + m |' + | l 2

2, n + m - 2

| ^- I I 2, n - m + 2 | )

-

- 1 ^m .

V ‘            ^{- 2} i ( ^{m - 1} ) ф     *

---2---^Re{ e  ^{v 7}  ( I 0, n + m I 2, n - m + 2

*

I 2, n + m - 2-

Для поперечных компонент СУМ общие выражения громоздки, но если принять за фокальную плоскость z = 0 и если в начальной плоскости комплексная амплитуда A ( 9 ) вещественна, то функции I 0, n , I 1, n , I 2, n также вещественны и тогда при m = 1 радиальная составляющая плотности СУМ равна нулю. При этом азимутальная составляющая имеет вид:

s ф = ( ¹ 0, n - 1 ^{- 1} 0, n + 1 ^{+ 1} 2, n + 1 ^{- 1} 2, n - 1 ) ¹ 1, n . ⁽¹⁶⁾

Это выражение отличается от выражения для продольной составляющей. Однако если фокусируется радиально поляризованный узкий кольцевой пучок, то есть A ( 6 ) = 5 ( 0 - О с ), то

S Ф

М

sin³ 6 0 cos²

6 0 J n ( kr sin 6 0 ) x

x [ J n — i ( kr sin 6 с ) - J n + i ( kr sin 6 0 ) ] .

Однако в случае седловой поляризации, в отличие от радиальной, в фокальной плоскости есть точки, в которых продольная составляющая СУМ равна нулю, а поперечная отлична от нуля (фотонное колесо). Так, на рис.3 показаны двумерные сечения распределений радиальной, азимутальной и продольной составляющих вектора плотности СУМ для радиальной и седловой поляризации, построенные вдоль оси x .

Из (17) видно, что 5 _Ф = 0, когда аргумент функции Бесселя равен нулю функции Бесселя или её производной, то есть на тех же радиусах (14), на которых обращается в ноль и продольная компонента плотности СУМ.

4. Плотность СУМ в остром фокусе оптического вихря с седловой поляризацией

В случае седловой поляризации y i- = у ₂₊ = 0, Y 1 ₊ = у _2-=1/2. Продольная компонента плотности СУМ при этом равна:

а)

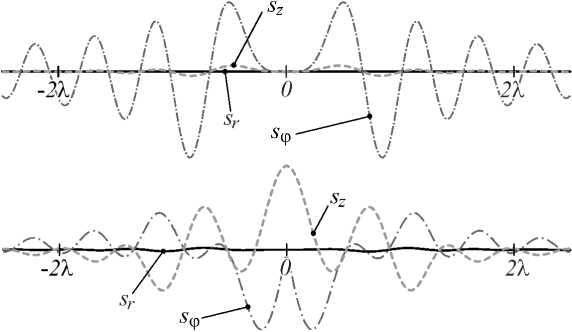
Рис. 3. Сечения распределений радиальной (кривые sr ), азимутальной (кривые 5Ф) и продольной (кривые Sz ) составляющих вектора плотности СУМ для радиальной (а) и седловой (б) поляризации

б)

2, n + m + 2

I ⁺ I^{2 2}

2, n - m - 2

+

( - 1 ) m     ,

^{- 2} i ( m ^{+ 1} ) ф * J

⁺ 2 Re { e        ( ² 0, n + m² 2, n - m - 2

-

*

2, n + m + 2 ² 0, n - m

Из (18) и аналогичных выражений для поперечных компонент следует, что в отличие от случая радиальной поляризации при m = 1 распределение плотности СУМ не обладает вращательной симметрией.

5. Численный расчёт плотности СУМ узкого кольцевого пучка с поляризационными сингулярностями в окрестности острого фокуса

На рис.2 показаны распределения продольной составляющей плотности СУМ узкого кольцевого пучка в фокальной плоскости для радиальной и седловой поляризации, рассчитанные по формулам (4). При расчёте использовались следующие значения параметров: длина волны X = 532 нм, фокусное расстояние f = 100 X , угол конических волн пучка 6 ₀ = 85°, топологический заряд оптического вихря n =3.

Из рис. 3 а видно, что в случае радиальной поляризации действительно компоненты s_r и s _Ф равны нулю при одних и тех же значениях радиальной координаты r . Однако фотонное колесо всё же формируется, но не точно, а приближённо, когда продольная компонента СУМ не равна нулю, но азимутальная компонента во много раз её превосходит. На рис. 3 б видно, что при седловой поляризации в центре картины (в самом фокусе) вектор плотности СУМ ориентирован продольно, в то время как вокруг центра имеется кольцо, на котором продольная компонента СУМ равна нулю, а азимутальная компонента сравнима с продольной компонентой в центре. На этом кольце и формируется фотонное колесо.

а)

Рис. 2. Распределения продольной составляющей вектора плотности СУМ (в условных единицах) узкого кольцевого пучка в фокальной плоскости для радиальной (а) и седловой (б) поляризации (чёрный цвет – минимум, белый цвет – максимум)

б)

На рис.2 видно, что в случае радиальной поляризации продольная составляющая обладает вращательной симметрией, а в случае седловой – только симметрией относительно декартовых координат.

Заключение

В данной работе получены выражения для радиальной, азимутальной и продольной компонент вектора плотности СУМ вблизи острого фокуса оптического вихря с поляризационной сингулярностью (с радиальной, азимутальной и седловой поляризацией). Для азимутальной поляризации установлено, что вектор СУМ ориентирован продольно (100% магнетизация [2]). Для радиальной поляризации показано, что вектор СУМ может иметь ненулевую азимутальную составляющую, при этом другая поперечная составляющая, радиальная, равна нулю. Численное моделирование на примере узкого кольцевого пучка показало, что при радиальной поляризации в фокальной плоскости есть области, где азимутальная компонента СУМ на порядок превосходит продольную, но обе они обращаются в нуль одновременно. В случае седловой поляризации есть области, где продольная компонента строго равна нулю и вектор плотности СУМ ориентирован азимутально.

Работа выполнена при поддержке Российского научного фонда (грант 17-19-01186) в частях «Численный расчёт плотности СУМ узкого кольцевого пучка с поляризационными сингулярностями в окрестности острого фокуса» и «Плотность СУМ в остром фокусе оптического вихря с радиальной поляризацией», Российского фонда фундаментальных исследований (грант 18-07-01129) в части «Общие выражения для плотности СУМ в остром фокусе светового поля с поляризационной и фазовой сингулярностью» и грант 1807-01380 в части «Плотность СУМ в остром фокусе оптического вихря с азимутальной поляризацией», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «Плотность СУМ в остром фокусе оптического вихря с седловой поляризацией».