По ту сторону интенсивности, или моменты интенсивности и измерение спектра оптических вихрей сложных пучков

Среди множества первостепенных проблем современной сингулярной оптики ключевым направлением исследований является формирование сложных сингулярных пучков, их разделение на парциальные вихревые пучки, измерение орбитального углового момента (ОУМ) и спектра оптических вихрей [1, 2]. Эти исследования находят отражение в ряде прикладных задач, например, в системах уплотненной передачи информации через многомодовые оптические волокна [3], в квантовом перепутывании состояний в узлах квантовых компьютеров [4], в оптической криптографии [5] и т.д. В данной работе мы сфокусируем внимание только на системах разделения парциальных сингулярных пучков в массиве оптических вихрей на основе голографических фильтров. Основные принципы и физические процессы, лежащие в основе селекции (разделения, сортировки) оптических вихрей, можно найти, например, в работах [6–10] и списке литературы в них. Формирование сложных сингулярных пучков и их разделение на стандартные вихревые пучки фактически являются зеркально симметричными процессами. Сложный сингулярный пучок формируется с помощью голографического фильтра на основе компьютерного моделирования голограммы таким образом, чтобы каждому парциальному исходному пучку с заданным значением топологического заряда оптического вихря соответствовало пространственное положение в прямоугольных или полярных координатах. Восстановленный пучок представляет собой комбинацию парциальных когерентных пучков с общей оптической осью. После прохождения оптической системы комбинированный пучок (массив оптических вихрей) падает на тот же оптика. – 2018. – Т. 42, № 5. – С. 736-743. – голографический фильтр. На выходе фильтра формируется пространственный веер стандартных пучков. Каждой пространственной координате светового веера в поперечном сечении соответствует конкретное значение топологического заряда. Известно однозначное соответствие между величиной топологического заряда m и значением ОУМ ℓz, приходящийся на один фотон m = ℓz для каждого элементарного сингулярного пучка (см., например, [11] и список литературы). Измеряя нормированную интенсивность в каждом парциальном пучке, можно построить гистограммы (линейчатый спектр) интенсивности и ОУМ массива оптических вихрей. В данной работе мы не будем обсуждать проблемы разрешающей способности и влияние перекрестных помех. Они достаточно подробно рассмотрены в ряде статей (см., например, [12]). Отметим только, что данный подход ограничен исключительно измерением интенсивности и опускает из внимания измерение начальной фазы парциальных пучков. Это существенно ограничивает дополнительное число степеней свободы в системах передачи информации. На этой проблеме мы остановимся подробнее в дальнейшем изложении.

Поставим вопрос об измерении ОУМ массива вихрей несколько иначе. Возможно ли измерить ОУМ всего массива, а не каждого вихревого пучка в отдельности? Такой вопрос правомерен, например, для пучков с дробными топологическими зарядами (см., например, [13, 14] и списки литературы). Действительно, авторам статьи [15] удалось измерить полный ОУМ различных массивов вихрей, используя единственную цилиндрическую линзу. Ключевым моментом в этом процессе является подход на основе моментов интенсивности jj x yq 3( x, y) dx dy

J =                        ,

^,       jj 3 ( x , y ) d x d y

S

где x , y – координаты точки в поперечном сечении S , 3 ( x , y ) - распределение интенсивности, p , q - целые числа.

Распределение Вигнера было впервые введено Юджином Вигнером [16] для анализа квантовых поправок к классической статистической физике в 1932 г. и адаптировано М. Ху [17] в 1962 г. для цифрового анализа оптических изображений в форме выражения (1). Заметим, что более общее выражение для моментов интенсивности включает в себя также импульсы (координаты волнового вектора) и позволяет упростить анализ распространения параксиальных пучков в оптической системе (см., например [18, 19] и списки литературы). Например, моменты J 0,1 и J 1,0 характеризуют положение «центра тяжести» пучка в поперечном сечении, моменты J 0,2 и J 2,0 задают радиусы перетяжки пучка вдоль оси x и y , соответственно, а комбинация моментов

^J 3,0

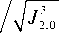
и J _0,3

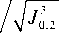
задаёт скручивание пучка вдоль осей x и y , соответственно. Авторы работы [15] нашли однозначное соответствие между моментом интенсивности J 1,1 = J_x , y ( x , y ) в выражении (1) в фокальной плоскости цилиндрической линзы и ОУМ и измерили величину ℓ z для пучков как с целым, так и с дробным топологическим зарядом. Мы задали себе вопрос: возможно ли измерить как ОУМ массива оптических вихрей, так и квадраты амплитуд и начальных фаз комбинированных пучков.

Таким образом, целью настоящей работы явилась теоретическая разработка метода измерений квадратов амплитуд C m , начальных фаз в m и ОУМ I z комбинированных сингулярных пучков, переносящих N оптических вихрей с топологическими зарядами m в случае невырожденного и чисто вырожденного состояния оптических вихрей.

1. Модель массива вихрей и метод измерений

В общем случае сложный массив оптических вихрей удобно представить в виде разложения по эле- ментарным параксиальным пучкам в виде ортогональных полиномов с гауссовой огибающей [20, 21]. Представим простейшую модель комбинированного пучка с массивом оптических вихрей в виде разложе- ния по скалярным пучкам Лагерра – Гаусса низшего порядка в плоскости перетяжки z =0

N

^(r, ф, z = 0)= £ «И. = m=-N

N C m r m e ⁽ m ^ m ) G ( r )

= S              ’

m=-N       Nm где G = exp(-r 2), ф - азимутальный угол, r = ^ x2 + y2 / w0 - нормированная радиальная коор дината, Nm = ^j 2 m 1 m !п - нормировочный множи тель, Cm и pm - амплитуды и начальные фазы парциальных пучков.

Сначала ограничим наш анализ невырожденным случаем, когда комбинированный пучок включает в себя только N пучков с одинаковым знаком топологического заряда: m >0 или m <0. Как мы увидим далее, такое ограничение является существенным для выбранных для анализа функций момента интенсивности M p , q ( r , ф ).

Запишем распределение интенсивности в виде

N-1 z~’23( r, ф) = Т*Ф = £ -m-r2 mG2 +

m S N m

N -1 C C

+2 у n m r m0, NmNm m ^ n

, m + n

cos [ ( m - n ) ф] X

N -1

m,n m, n=0, m * n c c n m m+m

------r X

N m N m

^X sin [ ( m ^- n ) ф] sin P m , n G 2 ,

Где в mn = в m в n .

Зададимся целью найти систему уравнений для комбинации моментов интенсивности J p , q , включающих в себя только квадраты амплитуд С_m ² и только перекрестные члены     X mn = C m C n cos в mn    и

X mn = C m C n sin в mn . Для этого перепишем моменты интенсивности (1) в более общем виде с функцией моментов M p , q

J

p , q

jj ^Mp , q ( x , у )³( x , у ) d x ^d у

S jj 3( x, y) dx dy

S

Для выделения первого члена в уравнении (3) используем функцию момента интенсивности в виде

M p = r 2 p , P = 2,1,2,..., N .                     (5)

Подставляя в (4) выражения (3) и (5), получаем систему N линейных уравнений для квадратов действительных амплитуд С_m ² :

₌ N ( rn ⁺ p ) ^!

J 2 ^p ^42?^ m ! C m ^, ,                    (6)

p = 1, 2, 3, ..., N - 2.

В левой части уравнений (6) стоят моменты интенсивности

J ₂ p = jj r ^{2 p} 3 ( r , ф ) d 5 ,                               (7)

S которые можно измерить в эксперименте, а в правой части - искомые величины ICmI2. Площадь d5 = rdrdф. Чтобы система уравнений стала замкнутой, полагаем p = 1/2 и находим

N —¹

V J 2,0 + J 0,2 = S         r ( m + 1/2 ) C m .         (8)

m =0 4V2 m !

Для нахождения перекрёстных членов X m и Y m выберем функции моментов в виде

M P ) = r” cos P ^ и M P ) = r p sin P ^ ■

После подстановки получаем

^J 2 ( P +1 ) ,1

2 2 ^{( p + 1 )}

N -1 p

EE m=0, k=0

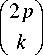
M

--— X

^Nn^Nn 1

^{X X}m . - 1

+ ^Mm . - 2

^Nm^Nn 2

X m,n2

;

J

1.2 ( P +1 )      2 2 ( P +1 )

N -1 P

EE (-1)P- k x m=0, k=0

X

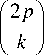
^Mm . - Y + M m . - 2 Y

_{NmNn 1}   m , n 1    _{NmNn 2}   m , n 2

где

- 1 = I m - 2( p - k ) ± 3I, - ₂ = I m - 2( p - k ) ± 11,

J 1,2( p +1) = JJ r 2 p ⁺ 3 sin 2 ⁽ p ^{+ 1)} Ф cos Ф d r d ф ■ S

Полученная система 3 N -уравнений ставит во взаимно однозначное соответствие множество моментов интенсивности с множеством квадратов интенсивности С_m ² и перекрёстных членов X m и Y m . Разность начальных фаз p -m находим как tg p -m = Y m / X m ■ Если задать p o = 0, то можно найти все остальные начальные фазы р _m из системы линейных уравнений Р -m = Р m Р - ■

Это значит, что моменты интенсивности вырождены относительно знака топологического заряда оптических вихрей. Отсюда следует, что уравнения (6), (7), (9), (10) нельзя использовать для вырожденных массивов вихрей. Однако имеется исключение, которое мы назвали чисто вырожденным состоянием, когда C m = C –m и начальная фаза принимает два значения р m = 0, п . В этом случае можно использовать уравнения (6), (7) и (9).

M

M ₌ f ^{m + -1} 2 ⁺¹_G2_d m , n _1,2                                     ^.

В левой части (9) и (10) стоят измеряемые моменты интенсивности

J 2( p +1)1 = JJ r 2 ^{P + 3}cos 2( ^{P + 1)} Ф sin Ф d r d ф и S

2. Эксперимент

На основе вышеописанного метода измерений квадратов коэффициентов вихревых пучков волнового массива была разработана экспериментальная установка, приведенная на рис. 1, которая позволяет измерять не только спектр вихрей, но и ОУМ массива.

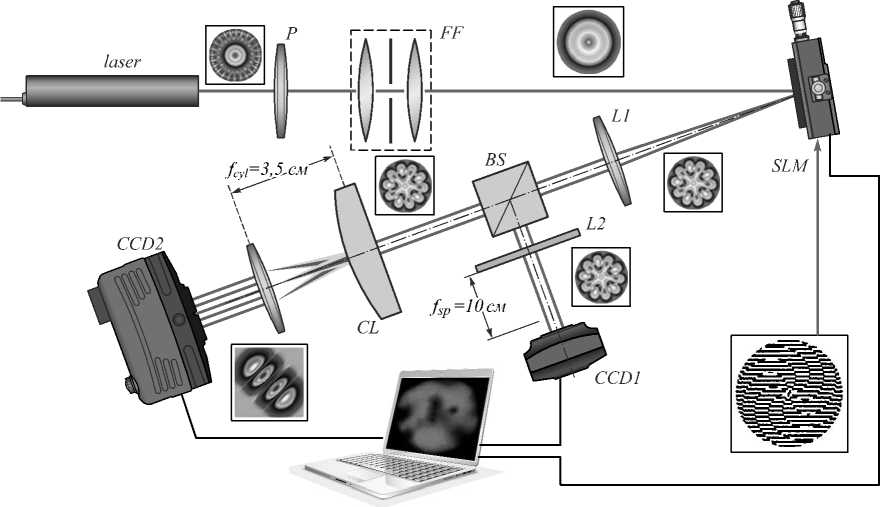
Рис. 1. Экспериментальная установка для измерения спектра вихрей и ОУМ массива сингулярных пучков. P – поляризатор, FF – пространственный фильтр, SLM – пространственный модулятор пучка (3840×2160 пикселей), L1, L2 – сферические линзы с фокальным расстоянием f L1 = 20 см и f sp = 10 см, BS – делительная призма, CL – цилиндрическая линза с фокальным расстоянием f cyl = 10 см, CCD1,2 – CCD-камеры (1920×1280 пикселей)

Свет от основной моды He-Ne лазера ( X =0,628 мкм) проходит через поляризатор P, пространственный фильтр FF и попадает на пространственный модулятор SLM. Жидкокристаллический элемент модулятора управляется с помощью компьютера, программа которого создает требуемый рельеф голографической ре-

шетки. Отраженный пучок переносит массив оптических вихрей с заданными значениями амплитуд C m , начальных фаз р m и топологических зарядов m ■ Далее комбинированный пучок расщепляется делительной призмой BS на два плеча. В первом плече сферическая линза L2 ( F = 10 см) проецирует комбинированный пу-

чок на входное окно ССD1-камеры, расположенное в фокальной плоскости сферической линзы. CCD1-камера сопряжена с компьютером.

Во втором плече сферическая линза L1 ( F =25 см) отображает пучок в плоскость цилиндрической линзы LC ( F =3,5 см). В свою очередь, цилиндрическая линза проецирует пучок на входное окно CCD2-камеры, расположенное в фокальной плоскости этой линзы. CCD2-камера также сопряжена с компьютером. Выходные сигналы SLM модулятора и обеих ССD камер синхронизированы между собой таким образом, чтобы результаты измерений выводились на экран монитора в реальном масштабе времени.

Предварительно измерялись перетяжки комбинированных пучков в плоскости ССD1-камеры в первом плече и в плоскости цилиндрической линзы CL в соответствии с формулами, приведенными в параграфе 1. Измерение перетяжки комбинированного пучка осуществлялось перед всем циклом измерений.

В общем случае комбинированный пучок имеет сложную форму поперечного сечения. Поэтому в обоих случаях измерялись перетяжки для сферических линз:

_w ( i )_=/( i ) h/^jM _w( 2 *=./( ² * _w² = j²^

w x J 2,0 ’ w y J 02 ’ w x J 2,0 ’ w y J 02

и вычислялась средняя перетяжка w1 = (wX1* + wУ**) /2, w2 = (wf* + wУ2)) / 2

в первом и втором плече соответственно. Естественно, такое приближение не дает точного результата и при вычислениях возникает определенная погрешность. Но конечные результаты всегда сравниваются с исходными значениями. Как показали дальнейшие калибровочные измерения, допускаемое приближение является достаточным. В процессе вычислений все длины под интегралами для моментов интенсивности и ОУМ нормировались на радиусы этих перетяжек.

Для определения квадратов амплитуд и начальных фаз решались уравнения (6), (7), (9), (10). При калиб- ровочных измерениях компьютер задавал значения амплитуд и фаз в режиме случайных чисел. Измерения ОУМ проводились согласно методу, подробно описанному в работе [15] согласно формуле

4л

I = — J z                xy

^ fcyl

4 л f

X

ff x • У -3 cyl ( X ’ y) dS

X             --- ff 3 cyl ( X ’ У ) dS

S

На рис. 2 приведено теоретическое ( а ) и экспериментальное ( б ) калибровочное распределение интенсивности на входном окне CCD1- камеры, а на рис. 2 в изображён вид амплитудной голографической решётки на SLM-модуляторе, формирующей комбинированный пучок.

а)

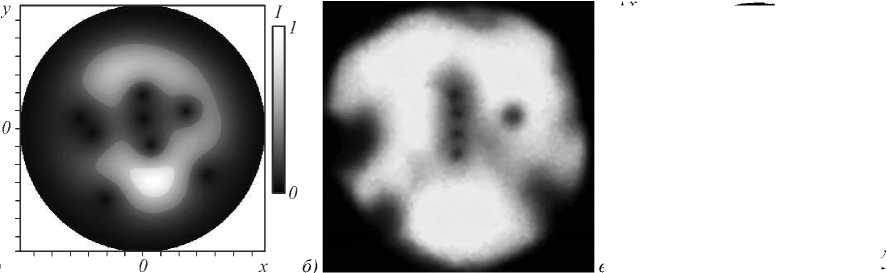
Рис. 2. Типичное теоретическое (а) и экспериментальное (б) распределение интенсивности (1920×1280 пикселей) на входном окне CCD1-камеры для массива из N=10 пучков и соответствующая амплитудная голографическая решётка на SLM модуляторе (в)

Результаты калибровочных измерений иллюстрируют гистограммы на рис. 3. Параллельно измерялись ОУМ во втором плече экспериментальной установки. Измерения показали, что в случае калибровки устройства орбитальный угловой момент всего комбинированного пучка равен ℓ z =4,2, а расчёт по формуле (11) даёт ℓ z = 3,9. На гистограммах приведена зависимость квадрата амплитуды C, ^ (рис. 3 а ) и начальной фазы Р _и от топологического заряда m парциальных вихрей. Сравнение теоретических и экспериментальных результатов показало, что относительная ошибка измерений квадрата амплитуды не превышает 5%, фазы – 6–7 %. Для величины ОУМ ошибка составила 4 %.

Вторую серию измерений мы проводили для случая чисто вырожденного состояния. Величины амплитуд задавались выражением Cm = (–1)m sinn (am), где a – частотный параметр, n = 1, 2, 3, .... Знак (–) указывает на скачок фазы на л.

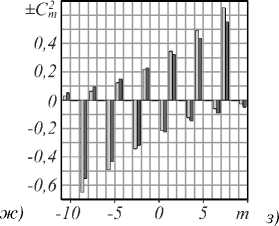
Результаты теоретического расчёта и эксперимента массива с N =21 представлены на рис. 4.

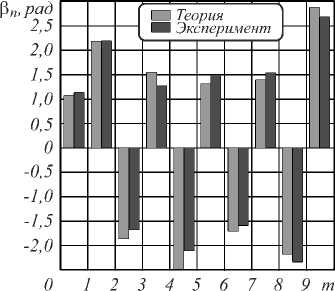
Рис. 4 а - в – иллюстрируют теоретическое распределение интенсивности 3 ( x, y) при изменении частотного параметра а в сотом знаке после запятой и n = 7. Рис. 4 г-е иллюстрируют 3 ( x, y), изменённые после модулятора SLM, рис. 4 ж-и задают экспериментальный и теоретический спектр вихрей парциальных пучков, а рис. 4 к-м иллюстрируют распределение интенсивности при значениях амплитуд и фаз, заданных экспериментальным спектром вихрей на рисунках рис. 4 г-е . Заметим, что даже очень малые изменения параметра a регистрируются экспериментально в спектре вихрей.

а)

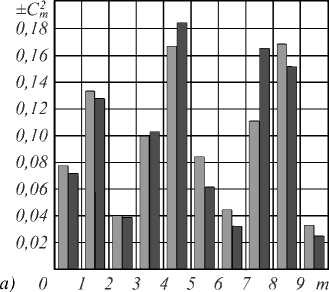
Рис. 3. Спектр вихрей волнового массива N=10: С_m ² (m) (а), β _m(m) (б). Дробный ОУМ: теория ℓ z =3,9, эксперимент ℓ z =4,2

г)

д)

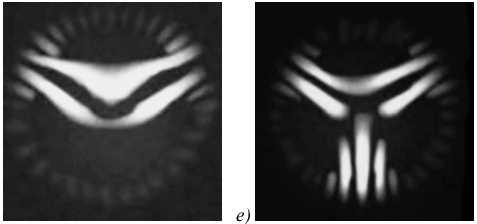
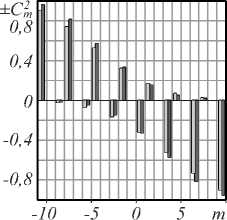
Рис. 4. Чисто вырожденное состояние волнового массива: теоретическое распределение интенсивности (а–в); распределение интенсивности после модулятора SLM (г–е); совмещённый спектр квадратов амплитуд C_m ² и фаз β m (ж-и); распределение интенсивности, полученное при восстановлении структуры пучка с амплитудами и фазами, приведёнными на гистограммах (к–м). Отрицательным значениям C_m ² соответствует скачок фазы на π .

Нижняя строчка соответствует степени корреляции η между исходным распределением интенсивности ℑ (x,y), амплитудами и фазами согласно спектрам (к–м): η =0,83 (к), η =0,89 (л), η =0,84 (м)

Для оценки погрешности измерений мы использовали функцию корреляции между исходным распределением интенсивности 3 th (x, y) и экспериментальными значениями 3 ex (x, y) со спектром вихрем, полу- ченным на эксперименте, согласно соотношению

Я ³ th ( x , У )³ exp, ( ^x , y ) d ^S

n = ----»—

th exp

^J 00 ^J 00

.

Полученные результаты степени корреляции располагаются в интервале n =0,83^0,91, что указывает на хорошее согласование теории и эксперимента.

Таким образом, мы разработали основы метода измерения спектрального состава вихрей в сложных невырожденных комбинированных сингулярных пучках, а также в чисто вырожденных массивах оптических вихрей, который основан на регистрации моментов интенсивности J p , q в плоскости перетяжки. При этом световой пучок не подвергается каким-либо преобразованиям, разрушающим структуру волнового фронта. Это позволяет измерять как квадраты амплитуд С_m ² , так и начальные фазы парциальных пучков. Высокая степень корреляции n между исходным распределением интенсивности и распределением интенсивности, построенным согласно экспериментальному спектру вихрей, указывает на надежность представленного метода измерений без разрезок и склеек волнового фронта. Для измерения спектра вихрей с различной степенью вырождения относительно знака топологического заряда требуется измерение моментов интенсивности при астигматичном преобразовании пучка, что будет рассмотрено в дальнейших работах.