Податливость газодинамического подшипника с эластичным компенсатором перемещения

Подшипники, обеспечивающие отсутствие контакта между движущейся деталью и корпусом, находят широкое применение в технике. Их преимуществами являются чрезвычайно малое трение и отсутствие износа даже при высоких частотах вращения. В качестве смазочных

Интерес вызывают газодинамические подшипники, в которых несущая способность слоя газовой смазки создается за счет гидродинамического эффекта [1]. Такие подшипники находят применение в малонагруженных приборах и в некоторых видах технологического оборудования [1]. Их применение в машиностроении ограничивается по причине малой несущей способности и высокой податливости, для снижения которой традиционными методами приходится уменьшать рабочие зазоры подшипников либо увеличивать их частоту вращения и диаметр. При этом возникают очевидные конструкторские и технологические ограничения.

В настоящей работе предложен и рассмотрен газодинамический подшипник с активным управлением положения смазываемых элементов. Конструкция подшипника показана на рис. 1.

Цапфа 1 поддерживается газовым слоем 2, разделяющим поверхности цапфы и опорной втулки 3 при вращении. В отличие от традиционной конструкции подшипников опорная втулка 3 выполнена подвижной. Возможность её смещения обеспечивается эластичной прокладкой 4. Во втулке 3 выполнены отверстия 5, выходящие в непроточные полости 6, образованные эластичной прокладкой 4, корпусом 7 и опорной втулкой 3. При вращении цапфы 1 в несущем слое подшипника возникает газовый клин, разделяющий поверхности цапфы 1 и опорной втулки 3. При этом в нагруженной и разгруженной областях подшипника в соответствующих полостях 6 компенсатора, в которые смазка без сопротивления попадает из несущего слоя 2 через отвер-

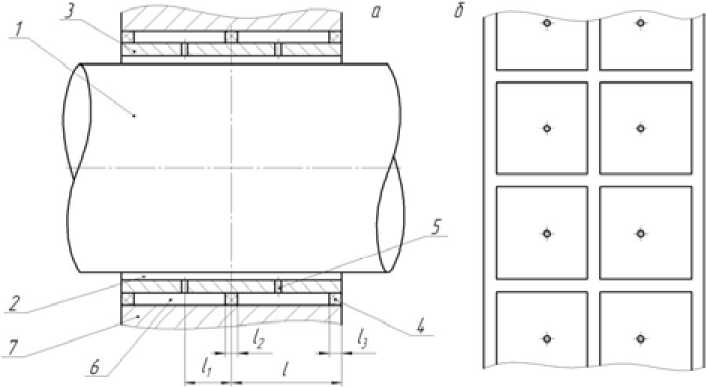
Рис. 1. Газодинамический подшипник: а – осевой разрез; б – развёртка эластичной прокладки и опорной втулки стия 5, повышается и понижается давление, под действием чего происходит смещение опорной втулки 3 навстречу вектору внешней силы. Этот эффект обеспечивает снижение суммарной податливости цапфы относительно корпуса подшипника.

Математическое моделирование

Функция давления p ( z , ф) в несущем газовом слое подшипника удовлетворяет краевой задаче для дифференциального уравнения Рейнольдса [2]

• 1    д Г, д p ) д ( . д p ^      д( ph )

• --—I h p — 1 +--I h p — 1 = 6u®——-,

r 0 д ф (   д ф ) д z ( д z ) дф                       _m

( )

p (z, 0) = p (z, 2n), |p (z, 0) = |p (z, 2n), |p (0, ф) = 0, p (l, ф) = Pa, дф дф      дz где z, ф - продольная и окружная координаты; r0 - радиус цапфы; 1 - половина длины подшипника; μ – динамическая вязкость газовой смазки; ω – угловая скорость вращения цапфы; h(ф) = h0 - e cos ф - функция зазора в смазочном слое; h0 - толщина слоя смазки при центральном положении цапфы; e – эксцентриситет цапфы и втулки; pa – давление окружающей среды.

При достаточно большом числе секций эластичной прокладки 3 функцию распределения давления в компенсаторе 6 можно считать моногармонической и давление в них приближенно описать одномерной функцией p ( 1 1 , ф), где 1 1 - расстояние от поперечной плоскости симметрии подшипника до плоскости расположения отверстий 5, через которые сжатая смазка поступает в полости компенсатора.

Расчет податливости подшипника проведен в безразмерной форме. За масштабы основных величин приняты: наружный радиус r ₀ для линейных размеров, p a - для давлений, 2п r ₀ ² p a - для сил, h ₀ - для смазочного зазора и эксцентриситетов.

Безразмерным аналогом (1) является задача

4 H - - д - l+Af H > P д - WPM д ф (    д ф ) д Z (    д Z )     д ф

, х , х дР х х дР х х дР

- (Z ,0) = - (Z ,2п), — (Z ,0) =   (Z ,2-Л),—(0, ф) = 0, P (L, ф) = 1.

^{д ф        д ф       д} Z

Здесь H (φ) = 1 – ε cos φ – безразмерная функция зазора; ε – относительный эксцентриситет цапфы; L - половина безразмерной длины подшипника; P ( Z , ф) - безразмерная функция давления в несущем слое; Z - безразмерная продольная координата; Л = 6р.® r ₀2 / h 0 p_a - «число сжимаемости» газовой пленки [3].

Рассмотрим работу подшипника при малых поперечных перемещениях цапфы ε << 1. В этом случае задача (2) может быть упрощена посредством ее линеаризации. Нахождение ее решения проведем в комплексной форме [3]. Для этого положим

H(ф) = 1 - £e-iф, P(Z, ф) = 1 + U(Z)£e-iф.

После линеаризации ⁽²⁾ и разделения переменных, получим задачу для функции U ⁽ Z )

U ( I i ^Л) U i ^л , . U '(G) = 0, U ( L ) = 0.

Решением этой задачи является функция

iЛГch^Z 1) U ( z ) =              1 ,

X2 ( chXL   )

где X = V1 - iЛ.

Комплексная форма безразмерной несущей способности подшипника определяется выражением

2π L2π L где

W1 = - J J(P -1) eфdZdф=- J J Re {иEe-iф} e1фdZdф = А]Б, π00              π00

A _iЛ Г th^^ l J

¹ = I² 1           J .

Модуль главного вектора реакции несущего слоя подшипника равен действующей на цапфу внешней силе

I Ai| £ = F.

С наружной стороны втулки несущей способности противодействует сила

W2 = ^4 КP(L1,ФН]e"dZdФ=12/jRe{^(А>ee*dZdФ = A£ π00                   π00

где Rm – безразмерный наружный радиус втулки, L4 = L – 0.5L2 – L3, л _i^L4 Rm

A ² =    X ²

( ch XL1

[ chXT " *J'

Проекция эксцентриситета втулки и корпуса на главный вектор реакции подшипника определяется выражением

em = Km Re{ A1 A2} e,

где K_m – коэффициент податливости эластичной прокладки. Это соотношение представляет собой уравнение силового равновесия втулки.

Суммарный эксцентриситет цапфы и корпуса равен

- = - + -s           m.

Решив систему линейных уравнений (3) – (5), получим искомую формулу податливости подшипника относительно его корпуса в направлении действия главного вектора реакции несущего слоя

е

K =

F

_ 1 + Km Re {A - A2}

A 1

.

В предельном случае Л ^ да имеем A 1 = L, A ₂ = R m L 4 , поэтому при больших угловых скоростях вращения цапфы податливость подшипника может быть оценена с помощью более простой формулы

K =

1 — L 4 K m ( R m - 1 ) L

Результаты исследования

На рис. 2 представлены зависимости податливости K подшипника от «числа сжимаемости» Л. Кривая для K m = 0 (абсолютно жесткая прокладка) соответствует обычному газодинамическому подшипнику. В нем зависимость K (Λ) является монотонно убывающей функцией.

С увеличением K m , когда прокладка приобретает упругие свойства, податливость подшипника уменьшается и может достигать нулевого или отрицательных значений (цапфа относительно корпуса не смещается либо движется во встречном по отношению к внешней силе направлении). При этом зависимости K (Λ), как видно на рис. 2, приобретают унимодальный характер, который проявляется на них в виде экстремума-минимума.

Экстремальный характер кривых можно объяснить исходя из анализа эпюр функции |U(Z)|, которые показаны на рис. 3. Кривые характеризует продольную конфигурацию газового клина, который образуется в несущем слое подшипника в результате гидродинамического эффекта. При относительно малых значениях параметра Λ перепад давления в газовом клине, как видно на графиках, мал и наибольшие его значения приходятся на узкую область центральной части несущего слоя. Если питающие компенсатор отверстия расположены в этой части подшипника, то превосходство интегральной реакции постоянного по длине компенсатора давления, которое значительно превышает соответствующий показатель в несущем слое, способствует быстрому уменьшению податливости до ее минимального значения. С увеличением частоты вращения цапфы при умеренных значениях параметра Л размер газового клина быстро расши-

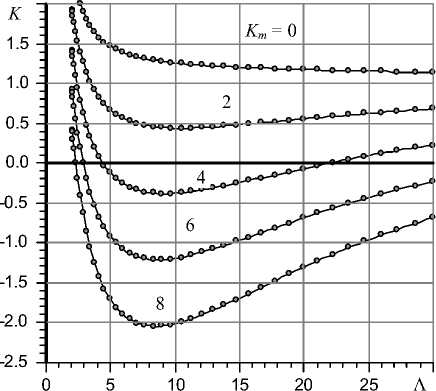
Рис. 2. Зависимости податливости K от «числа сжимаемости» Λ при различных значениях податливости

K_m эластичной прокладки, L = 1.5, L 1 = 0.2, L ₂ = L ₃ = 0.1, R m = 1.2

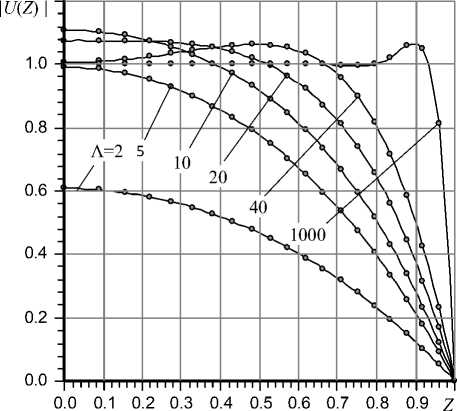
Рис. 3. Функция |U(Z) | при различных значениях «числа сжимаемости» Λ, L = 1

ряется, давление в нем возрастает, что влечет ослабление силового противодействия реакции несущего слоя со стороны сил давления в компенсаторе.

В результате этого при дальнейшем повышении частоты вращения цапфы функция податливости меняет свой характер и, достигнув своего минимума, начинает увеличиваться. При этом, как следует из анализа формулы (6), подшипник может обладать низкой положительной, нулевой и отрицательной податливостью при предельно высоких частотах вращения цапфы.

Упомянутый характер эпюр функции |U(Z)| позволяет управлять желаемым видом характеристики податливости K (Л) посредством назначения требуемого значения параметра L 1 , а также параметров L ₂ и L ₃. Как видно на рис. 4, чем больше значение параметра L 1 , тем больше и абсцисса минимума K (Λ).

С увеличением L 1 минимальные значения K в точках экстремума растут, однако их всегда можно уменьшить, увеличив податливость K m эластичной прокладки. Так, при L 1 = 0.25 оптимальным с точки зрения минимума податливости является Л ~ 9. Если L 1 = 0.5, то минимум податливости имеет место при Л ~ 32, а при L 1 = 0.75 оптимальным будет значение Л ~ 160.

На рис. 4 видно также, что с увеличением значений параметра L 1 характеристика податливости K (Λ) в области экстремума становится более стабильной.

Заключение

Представленная математическая модель статического состояния рассмотренного газодинамического подшипника, аналитическое решение дифференциальной задачи, полученное в комплексной форме, дают возможность выполнить исследование его статической податливости.

Полученные результаты позволяют сделать вывод о возможности существенного снижения податливости конструкции, а также достижения очень низких, нулевых и отрицательных – 662 –

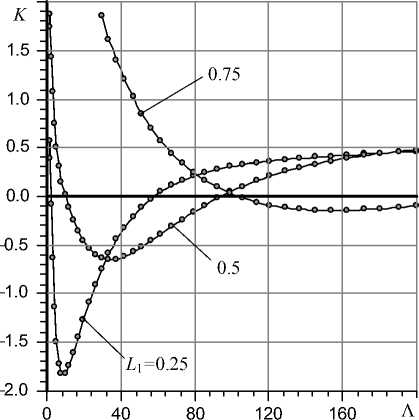
Рис. 4. Зависимости податливости K от «числа сжимаемости» Л при различных значениях параметра L 1 , L = 1, L 2 = L ₃ = 0.1, R m = 1.2, K m = 8

величин, когда такие подшипники способны компенсировать положительную податливость других элементов конструкций, в которых они используются.

Показано, что при соответствующем подборе конструктивных параметров можно получить требуемые статические характеристики подшипника.