Подавление помех на цифровых голографических изображениях

Для решения целого ряда задач обнаружения и идентификации различных объектов в объёмной среде в последние годы активно используются методы цифровой голографии. В частности, применяется осевая схема записи цифровых голограмм (схема Габора) [1, 2] с целью определения размеров, форм, координат и идентификации взвешенных частиц различной природы. Такие частицы встречаются достаточно часто в различных средах: в газах, жидкостях и твёрдых телах, образуя взвеси (золи) – многофазные системы, соответственно, аэрозоли, гидрозоли и солидозоли. Примерами таких взвесей и частиц, их образующих, являются: планктон и другие частицы в морской воде (морской снег, твёрдые неорганические частицы, газовые пузыри и т.п.), объёмные дефекты и включения в оптических материалах, аэрозольные частицы, капли в факеле распыла форсунок, эритроциты и др. Соответствующие применения, в частности, рассмотрены в работах [3, 4].

В качестве основных преимуществ методов цифровой голографии можно отметить следующее:

• 1)    возможность определения конкретных геометрических размеров объектов и их расположения в объёме образца с заданной точностью;

• 2)    возможность проведения исследований внутри среды без ограничения исследуемого объёма рабочим сечением объектива микроскопа, в том числе в средах с высоким показателем преломления в постэкспериментальном режиме;

• 3)    возможность записи и численного восстановления цифровых голограмм на длине волны 1,064 мкм материалов, непрозрачных в видимом диапазоне длин волн, но прозрачных в ИК-диапазоне, например, таких оптических материалов, как ZnGeP 2 , Ge и т.д. Это, в свою очередь, позволяет визуализировать дефектную 3D-структуру данных материалов, не видимую глазом человека, поскольку получаемые с ПЗС-матрицы изображения записываются в виде монохромного чёрно-белого изображения;

• 4)    возможность изучения каждого обнаруженного дефекта с достаточной для его идентификации детализацией в объёме матричного носителя, значительно превышающем размеры дефекта;

• 5)    возможность получения и хранения информации о пространственном положении дефектов, их ориентации и форме;

• 6)    возможность привязки координат каждого дефекта к точкам исследуемого объекта (объёма среды) и построения трёхмерного распределения частиц по объему;

• 7)    возможность проведения контрольных измерений в режиме реального времени, определяемых характерными временными интервалами изменения измеряемой величины;

• 8)    возможность синтеза апертуры для увеличения допустимого поперечного сечения исследуемого образца.

Среди преимуществ осевой схемы записи голограмм Габора можно обозначить простоту реализации оптической схемы записи цифровых голограмм и низкие требования к когерентности лазерного источника.

Однако одной из проблем, значительно ограничивающих потенциал применения методов цифровой голографии, является наличие помех на цифровых голографических изображениях. Эти помехи приводят к беспорядочно распределённому зернистому шуму в воспроизводимой интенсивности, фоновым флуктуациям, паразитным полосам и дифракционным петлям в восстановленном изображении. Случайное колебание интенсивности или фазы, генерируемое самим объектом, не меняется со временем и фактически содержит подробную информацию об исследуемом объекте. Флуктуация, генерирующаяся внутри системы по другим различным причинам, влияет на качество голографического изображения. Зачастую помехи являются следствием интерференционных взаимодействий волн, отражающихся от структурных дефектов исследуемого оптического элемента либо от его граней. Наличие помех значительно искажает голографические данные о размерах и местоположении дефекта или приводит к полной потере информации о дефекте [5].

Для решения этой проблемы на данный момент существует два основных класса подходов. Первый класс включает изменение оптической схемы записи голограммы, и второй – численное подавление помех. Наиболее известными методами первой категории является внеосевая, впервые предложенная Лейтом и Упатниексом, и осевая голографии [6]. Данные подходы оказываются менее подходящими для изучения набора небольших объектов из-за необходимости регистрации большого объема данных (цифровых голограмм) [7], которые восстанавливаются и с использованием специальных алгоритмов обрабатываются, что занимает длительное время и большие ресурсы памяти ЭВМ. Вторым классом методов подавления помех является метод усреднения по большому количеству изображений [8, 9]. Существует три метода усреднения:

• 1)    усреднение с использованием мультиспек-трального источника излучения на этапе регистрации цифровой голограммы [10];

• 2)    усреднение с использованием мультиспек-трального источника излучения на этапе восстановления цифровой голограммы;

• 3)    усреднение по нескольким цифровым голограммам [11].

Однако данные методы малоэффективны в данной задаче, так как, как и для внеосевой и осевой голографии, усреднение требует регистрации большого объёма данных для одного исследуемого объекта и большие ресурсы памяти ЭВМ.

В данной статье продемонстрирован разработанный программный модуль цифровой фильтрации (удаления) помех с восстановленных и исходных цифровых голографических изображений. Он позволяет сохранять «полезную» информацию о регистрируемых дефектах оптического материала при записи единичной голограммы.

• 1.    Используемое оборудование

В работе использовалась цифровая голографическая камера (ЦГК), которая представлена на рис. 1. В табл. 1 представлены характеристики используемой камеры.

Рис. 1. Цифровая голографическая камера ЦГК-1,064

Табл. 1. Характеристики ЦГК-1,064

	Характеристика	Значение
1	Длина волны	1,064 мкм
2	Мощность излучения	50 мВт
3	Поле зрения	100×80 мм
4	Разрешение матрицы	2048×2948 Размер пикселя – 3,5 мкм
5	Исследуемая толщина материала	50 см и более (в зависимости от коэффициента поглощения материала)
6	Частота кадров для записи динамических процессов	До 120 кадров в секунду
7	Интерфейс	Ethernet 1 Гбит/с

В цифровой голографической камере, представленной на рис. 1, используется способ визуализации, представляющий собой типичную осевую схему записи цифровых голограмм Габора (рис. 2) при ис- пользовании компьютерной обработки полученных изображений.

Источник 1 представляет собой лазерный диод с плоскопараллельным пучком света. Данный пучок проходит через коллиматор 2, образуя пучок необходимого диаметра, проходящий, в свою очередь, через исследуемый образец 3. Результатом прохождения пучка через исследуемый образец является формирование интерференционной картины, состоящий из ча- сти излучения, прошедшего через однородную часть образца без рассеяния на дефектах (опорная волна), и части излучения, рассеянного на дефектах и неоднородностях (предметная или объектная волна). Далее ПЗС-камера 4 регистрирует полученную интерференционную картину. Картина отправляется в память компьютера 5 в виде дискретного двумерного массива. Что и представляет собой, в конечном итоге, цифровую голограмму объема среды [12, 13].

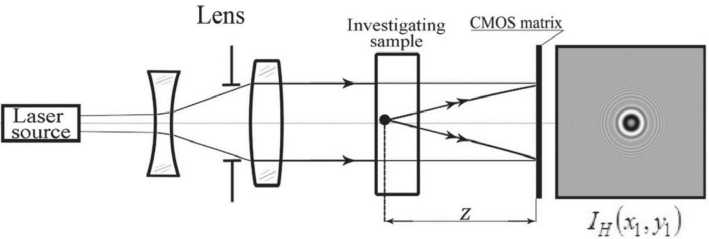
Рис. 2. Схема цифровой голографической камеры

Далее двумерный массив принимается как исходное распределение поля U(x1, y1) (с точностью до константы) в плоскости голограммы. Данное распределение при помощи численного расчета дифракцион- ного интеграла (1) позволяет рассчитать распределение поля в плоскости на заданном расстоянии от плоскости голограммы U(x2, y2), расположенной на расстоянии z от плоскости голограммы U(x1, y1) [14].

1 ? ?               ( 2 п Л Г i П            2 Z       ч2\ V .

и ( x 2 , у 2 ) =      [( U ( X У 1 ) exp I i — z I exp I     ( ( X i - x 2 ) + ( У 1 - У 2 ) ) | dx i dy i ,                                   (1)

i A,z                       A          z A

-^-^

где λ – длина волны, z – расстояние между плоскостью голограммы и плоскостью восстановления.

Соответственно, слой за слоем можно формировать изображение исследуемого объёма образца, меняя в интеграле (1) расстояние (шаг) z для расчёта распределения интенсивности в различных сечениях объёма образца, используемых в исследованиях. При этом на каждом восстановленном изображении поперечного сечения монокристалла визуализируются дефекты (неоднородности), что позволяет определить их трёхмерные координаты, форму, ориентацию, расположение в образце. Т.е. восстановление изображений происходит численно, при этом изображение исследуемого объема формируется в процессе обработки послойно. Такая методика может быть названа виртуальным микроскопом из-за сходства процесса послойного восстановления с процессом продольной наводки микроскопа.

На рис. 3 представлен пример цифровой фокусировки изображения дефекта в образце при помощи изменения расстояния между плоскостью записи голограммы и плоскостью восстановления цифровой голограммы в координатном пространстве. Восстановленные изображения формировались с шагом 300 мкм по координате z . На рис. 3 а наблюдается расфокусировка изображения дефекта в обе стороны от сфокусированного состояния в условной точке «0» рис. 3 б . Таким образом, плоскость, на которой формируется сфокусированное изображение дефектов, находится на таком же расстоянии от плоскости регистрации голограммы, что и реальный регистрируемый дефект.

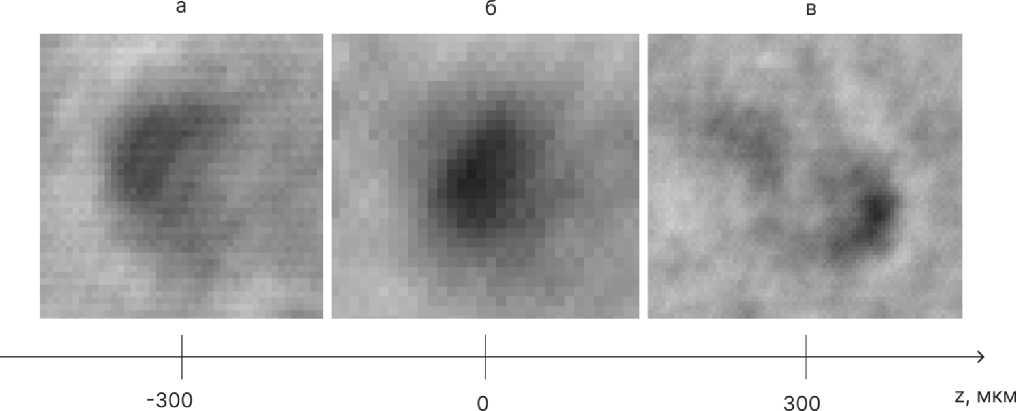
Рис. 3. Пример полной расфокусировки (а, в) и полной фокусировки (б) дефекта

В данной работе в качестве исследуемых образцов используются лазерноактивные и нелинейные оптические материалы, применяемые для генерации мощного излучения в среднем ИК-диапазоне: ZnS, ZnSe и ZnGeP 2 .

2. Алгоритм подавления помех от когерентных шумов

В рамках данной работы создан программный модуль цифровой фильтрации (селективный фильтр) по-

давления помех на восстановленных цифровых голографических изображениях и на голограммах. Фильтр основан на использовании оператора усреднения [15] и предназначен для обработки 8-битных изображений в палитре оттенков серого формата BMP. Данный формат используется в работе в силу поддержки им различных глубин цвета (1-, 4-, 8-, 16-, 24- и 32-битные изображения), простотой преобразования в матрицу и устойчивости к сжатию без потерь качества. Схема работы алгоритма подавления помех представлена на рис. 4.

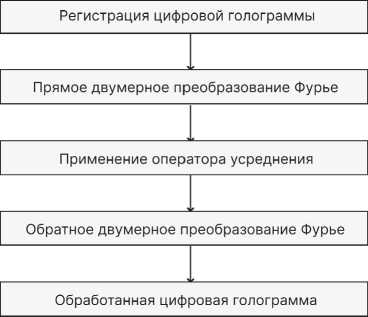
Рис. 4. Схема алгоритма подавления помех

На первом этапе работы фильтра к цифровому голографическому изображению в координатной плоскости применяется двумерное преобразование Фурье (ПДПФ).

Это позволяет получить функцию пространственных частот распределения интенсивности в плоскости записи цифровой голограммы или в плоскости восстановления цифрового голографического изображения. Выбор плоскости зависит от того, обрабатываем мы цифровую голограмму или уже восстановленное голографическое изображение координатной плоскости.

После применения ПДПФ на голографическом изображении в частотном пространстве помехам будут соответствовать артефакты, обладающие яркостью белого цвета ниже определенного значения в рамках палитры оттенков серого. Следует отметить, что наиболее значимая информация о распределении амплитуды и фазы, которая необходима для корректного обратного двумерного преобразования Фурье (ОДПФ) без потери «полезной» информации, находится в центре изображения и теряет свою информативность по мере удаления от него.

Для устранения помех используется алгоритм адаптивного размытия с пороговой обработкой. Алгоритм определяет пиксели с яркостью белого цвета в палитре оттенков серого ниже 50. Данное значение установлено экспериментальным путем для обеспечения максимально эффективного подавления помех на цифровом голографическом изображении при минимальной потере «полезной» информации о местоположении и форме дефектов на Фурье-

преобразованном изображении. Выбранным пикселям устанавливается среднее значение яркости окружающих пикселей, создавая эффект размытия. Этот процесс реализуется на основе матричной формулы оператора усреднения (2), тем самым приводя все пиксели Фурье-изображения к яркости, удовлетворяющей описанным выше требованиям.

A = 1

Последующее обратное двумерное преобразование Фурье приводит к получению цифрового голографического изображения в координатной плоскости полностью свободного от наличия помех при минимальных потерях «полезной» информации о неоднородностях и дефектах, регистрируемых в объёме образца. Результаты работы фильтра и их обсуждение представлены в следующем параграфе статьи.

3. Экспериментальные результаты работы и их обсуждение

Алгоритм фильтра определяет тёмные пиксели (с яркостью ниже 50 в палитре серого цвета) и устанавливает им среднее значение окружающих пикселей, создавая эффект размытия на основе матричной формулы оператора усреднения (2).

Для таких пикселей градиент устанавливаемых значений можно изменять путём суже-ния/расширения матрицы оператора усреднения в алгоритме размытия. Количество пикселей, которые

будут обработаны, можно регулировать параметром δ (пороговое значение). Он отвечает за значение яркости белого для пикселей, которые подлежат обработке. Пиксели, не попадающие в данный диапазон, остаются с прежним значением яркости. На рис. 5 представлен пример обработанного цифрового голографического изображения в частотной области пространства (Фурье-преобразованного изображения) вблизи его центральной части рис. 5 а .

Рис. 5 Пример обработки Фурье-преобразованного изображения фильтром, а) оригинал и б) обработанная версия

Было замечено, что при такой обработке возникает ситуация, когда через центр Фурье-преобразованного изображения проходит полоса тёмных пикселей, принимаемых алгоритмом за частотные составляющие помех. При этом экспериментально установлено, что любые изменения в центральной части Фурье-преобразованного цифрового голографического изображения в радиусе 25–45 пикселей от центра приводят к значительному ухудшению резкости как изображения в целом, так и изображения дефектов, или даже к полной потере информации о них.

На рис. 6 представлен пример такой обработки. На рис. 6 а показано исходное восстановленное изображение в координатном пространстве. На рис. 6 б представлено то же самое восстановленное изображение в частотной области, при этом к центру изображения в пределах прямоугольника площадью 35 пикселей применён разработанный цифровой фильтр. Вынесенный фрагмент изображения на рис. 6 б демонстрирует применение фильтра к центру изображения. Как упоминалось выше, такое выделение приводит к потере резкости и контрастности как самого изображения, так и дефектов на нём. На изображении рис. 6 в продемонстрировано восстановленное голографическое изображение после такой фильтрации с потерей резкости и контрастности изображения в координатном пространстве.

Также экспериментально установлено, что вне центральной части изображения в виде конусов с углом развёртки 45–90 градусов имеются области, при воздействии на которые сильно уменьшается резкость изображения и практически теряются некоторые дефекты при обратном преобразовании Фурье. На рис. 7 представлен пример обработки данных областей фильтром. Видно, что после обработки изобра- жения дефектов теряют резкость и контрастность, а некоторые дефекты становятся едва различимы. Такая обработка в дальнейшем приведет к неправильному поиску дефектов в материале по голограмме.

Рис. 6. Результат обработки фильтром центральной части Фурье-изображения, а) восстановленное цифровое голографическое изображение, б) Фурье-преобразование, в) обработанное изображение

Рис. 7. Пример обработки фильтром левой верхней и правой нижней части изображения

Для предотвращения ситуаций искажения информации на изображении в разработанный фильтр подавления помех было добавлено несколько функций, при помощи которых задаются области изображения, где обработка будет запрещена. Первая из этих функций задаёт радиус от центра (в пикселях), в котором размытие пикселей не будет происходить, даже если они попадают под критерий оператора усреднения. Вторая функция создает такую же защитную область, но в виде конусов с регулируемым углом развертки, начинающуюся в левой верхней и правой нижней части изображения частотного пространства. Расположение установлено экспериментально внесением изменений в этих четвертях, которые приводят к искажениям на изображении, при этом никак не влияют на помехи (зоны могут быть инвертированы при других режимах регистрации голограммы).

На основании результатов обработки был сделан вывод, что в частотном пространстве голограммы информация о помехах локализована и расположена диагонально вдоль изображения, а большая часть информации о дефектах расположена вблизи центра голографического изображения в частотном пространстве (рис. 8). В ходе экспериментальных работ с разработанным фильтром не было выявлено случаев появления случайных ложных изображений дефектов. Даже некорректная работа фильтра приводит лишь к ухудшению контрастности и четкости изображений, регистрируемых дефектов, что и отображено на рис. 6, 7.

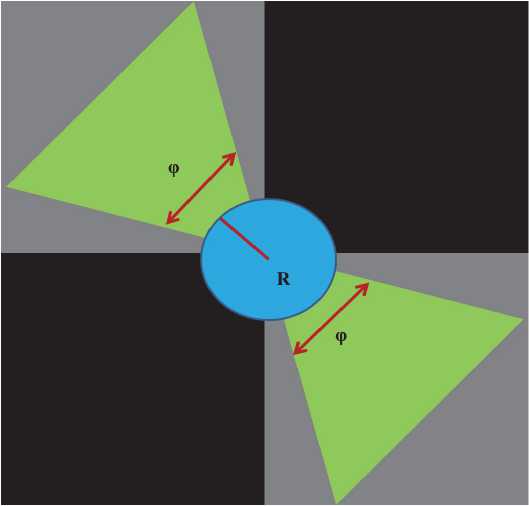
Рис. 8. Визуальное представление работы «защитных» функций фильтра, зеленым и синим цветом показаны области, защищенные от воздействия оператора Лапласа

Помехи условно можно разделить на две категории: концентрические круги, поперечные и продольные полосы, наблюдаемые в координатном пространстве голограммы. Как уже было сказано ранее, они появляются из-за интерференционных взаимодействий волн, отражающихся от структурных дефектов исследуемого оптического элемента, либо переотражений на границе раздела двух сред (от граней образца).

Причём, если сделать обратное действие и применить размытие к менее тёмным пикселям голографического изображения в частотном пространстве, то останутся только помехи (рис. 9). Как можно заметить, слева на восстановленном изображении отчётливо просматриваются дефекты, скрытые на фоне помех, а справа, после описанной обработки, различимы лишь шумовые полосы.

Рис. 9. Восстановленное цифровое голографическое изображение и его вид после обработки фильтром

Размытие тёмных пикселей голографического изображения в частотном пространстве при помощи селективного фильтра с защитными областями приводит к подавлению помех в координатном пространстве голограммы. На рис. 10 представлен результат работы фильтра на примере цифровых голографических изображений, содержащих изображения дефектов.

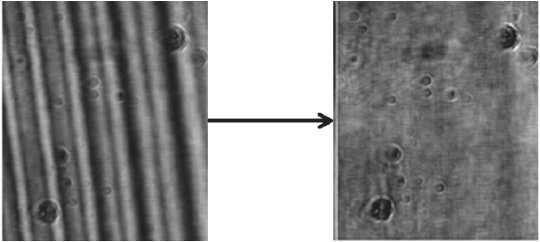
Рис. 10. Результат обработки восстановленного цифрового голографического изображения на примере фрагментов оригинала изображения рис. 6а и Фурье-преобразования рис. 5

После применения фильтра исчезли практически все концентрические круги, за исключением нескольких вблизи края образца. Данное исключение связано с тем, что цифровая голограмма представляет собой дискретную ограниченную функцию. Для расчёта восстановленного изображения использовалось матричное представление выражения (1), которое вычисляется с применением алгоритмов на основе быстрого преобразования Фурье. Однако за счёт конечных размеров апертуры голограммы, ограниченных размерами регистрирующей ПЗС-матрицы, на краях регистрируемых голограмм наблюдаются дифракция, приводящая к наличию дифракционных полос на краях цифровых голограмм. К сожалению, данный тип помех на цифровых голографических изображениях не удалось убрать при помощи разработанного алгоритма.

На остальных изображениях в координатном пространстве, которые представляют собой увеличенные фрагменты изображений до и после обработки, можно заметить, что там, где были полосы чёрного цвета, детализация дефектов частично отсутствует. Это можно обосновать изначальным отсутствием инфор- мации об этих частях дефектов на оригинальном восстановленном изображении из-за сильных искажений помехами.

Рассмотрим пример работы селективного фильтра на восстановленном голографическом изображении рис. 11. Изображению рис. 11 а соответствует исходная восстановленная цифровая голограмма в координатном пространстве, на которой видны значительные помехи в виде полос. Видно, что на изображении рис. 11 в после применения фильтра контрастных полос на голографическом изображении в координатном пространстве стало значительно меньше, особенно заметных в углах изображения. На вынесенных фрагментах рис. 11 а , в наглядно показано ослабление влияния помех на дефекты.

Рис. 11. Результат обработки восстановленного цифрового голографического изображения селективным фильтром, а) восстановленное цифровое голографическое изображение, б) фурье-преобразование, в) обработанное изображение

На рис. 12 представлен ещё один пример восстановленного голографического изображения до и после обработки. На рис. 12 а слева видны контрастные полосы от помех, после обработки на рис. 12 б они практически исчезают, за исключением областей возле верхнего и нижнего края изображения. При этом более мелкие полосы по всему остальному изображению удалены без ущерба детализации изображения.

Также работоспособность фильтра была опробована на исходной цифровой голограмме, записанной в формате BMP. На рис. 13 приведён пример обработки исходной голограммы и последующего восстановления цифрового голографического изображения.

На восстановленном изображении области дефектов остаются резкими, а большинство помех практически полностью исчезают. Однако сохраняются помехи по контуру, а также несколько сильных интерференционных полос около края голограммы и восстановленного изображения, что, скорее всего, связано с особенностями численного восстановления голограмм. Как показали проведенные тесты, после подавления шумовых составляющих голографическое изображение можно восстанавливать без ущерба для контрастности и детализации изображений дефектов и неоднородностей.

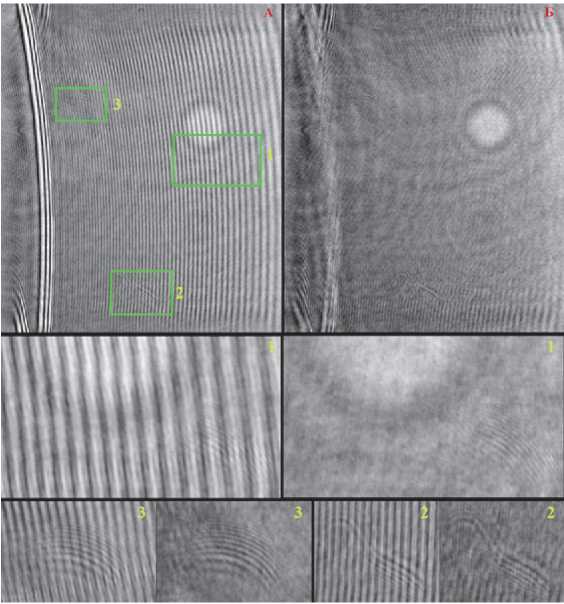
Рис. 12. Результат обработки восстановленного цифрового голографического изображения: а) оригинал,

б) обработанное изображение

Рис. 13. Результаты обработки голограммы фильтром: а), б) оригинал и обработанная голограмма, в), г) оригинал и обработанное восстановленное изображение в одинаковой плоскости

Оператор усреднения в представленных примерах применялся к правому верхнему и левому нижнему квадранту (I и III квадранты Фурье-спектра) Фурье-изображения голограммы. На рис. 10, 11, 12 наклон полос составляет, как правило, более 90°-180°. Гармоники пространственного спектра, соответствующие этим полосам, располагаются в I и III квадрантах плоскости Фурье-частот. Фильтрация в I и III квадрантах плоскости Фурье-частот приводит к ожидаемому результату. В случае рис. 13 наклон полос составляет существенно меньше 90°. Возможно, что гармоники от таких структур могут располагаться во II и IV квадрантах плоскости Фурье-частот, поэтому фильтрация в I и III квадрантах по разработанному алгоритму могла оказаться менее эффективной в данном случае. В дальнейшем необходимо рассмотреть условия применения фильтрации во II и IV квадрантах плоскости Фурье-частот для голографических изображений с подобным расположением помех в пространственной плоскости, с целью минимизации потерь полезной информации и улучшения качества фильтрации изображения. Вероятно, учёт общего направления периодических структур на изображениях позволит подобрать более гибкие условия применения оператора усреднения.

Заключение

Разработан алгоритм подавления помех как с исходных цифровых голограмм, так и с восстановленных голографических изображений, за счет применения эффекта размытия на основе оператора усреднения к Фурье-преобразованным цифровым голографическим изображениям в частотном пространстве. В ходе работы были экспериментально определены области изображений частотного пространства, в которых локализована «полезная» информация о регистрируемых объектах, и области, в которых локализована информация о помехах регистрируемых голограмм. На основе полученной информации была разработана функция защиты областей Фурье преобразованных цифровых голографических изображений, содержащих информацию о регистрируемых объектах. На основании результатов обработки показано, что после Фурье-преобразования цифрового голографического изображения информация о помехах локализована и расположена диагонально вдоль изображения, а большая часть информации о дефектах расположена вблизи центра изображения частотного пространства в радиусе 25–45 пикселей от центра голограммы.

По результатам обработки многочисленных цифровых голографических изображений было выявлено, что разработанный фильтр способен удалять помехи без потери информации о форме и местоположении регистрируемых объектов.

Как выявили экспериментальные исследования, данный фильтр не способен удалять помехи с восстановленных голографических изображений, вызванных конечными размерами голограммы. В целом, разработанный фильтр подавления помех применим для широкого спектра цифровых голографических приложений, при этом не требует больших ресурсов как оперативной памяти, так и процессора ЭВМ.

Результаты были получены в рамках выполнения государственного задания Минобрнауки России, проект № FSWM-2020-0038.