Подбор потенциала межатомного взаимодействия для бериллия

Актуальность исследования бериллия обусловлена использованием данного материала в проекте международного экспериментального термоядерного реактора (ИТЭР). Бериллий выбран в качестве материала защитных пластин для 80% поверхностей, взаимодействующих с плазмой. В связи с этим особенно важно исследовать следующие свойства данного материала: радиационная стойкость, стойкость к термоциклическим нагрузкам, распухание при взаимодействии с радиационным облучением. Исследование физических свойств бериллия, по причине его дороговизны и потенциальной опасности для здоровья, наиболее целесообразно производить с использованием компьютерного моделирования. Такое моделирование производится на различных уровнях детализации в рамках многомасштабного подхода. Для моделирования на атомномолекулярном уровне систем, состоящих из большого числа атомов, используются эмпирические потенциалы межатомного взаимодействия.

В настоящее время имеется небольшое количество работ по расчетным исследованиям свойств бериллия методами ab initio (см., например, работу [1]), а также подбору потенциала межатомного взаимодействия. Так в работах [24] для построения потенциала межатомного взаимодействия бериллия был выбран метод погру-

Прокофьев Максим Владимирович, младший научный сотрудник.

женного атома (embedded atom method, EAM). В EAM энергия системы, состоящая из набора атомов, представлена как сумма энергии парных взаимодействий и энергии, необходимой для внедрения («погружения») каждого из атомов в электронную плотность, создаваемую всеми остальными атомами.

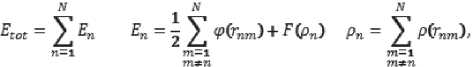
где E _tot – энергия системы из N атомов, с _n – электронная плотность в точке расположения атома n , которую создают все окружающие атомы, Р( r nm ) – электронная плотность, создаваемая атомом m в точке расположения атома n , F ( Р _n ) - энергия необходимая для того, чтобы поместить атом в электронную плотность Р_n , ф( r nm ) - парный потенциал взаимодействия между атомами n и m , находящимися на расстоянии r _nm .

Авторами перечисленных работ было достигнуто хорошее соответствие расчетных значений упругих постоянных, энергии связи и энергии образования вакансий с их экспериментальными значениями. Но функциональные зависимости ф( r ) и Р ( r ) подобранных потенциалов взаимодействия не связаны друг с другом, что не является физически обоснованным, так как парная часть взаимодействия в металлах также обусловлена распределением электронной плотности атома. По этой причине в данной работе для подбора потенциала межатомного взаимодействия бериллия был использован потенциал взаимодействия для чистых металлов, предложенный в работах В.Е. Зализняка и О.А. Золотова [5, 6]. В этих работах предлагается специального вида аппроксимация распределения электронной плотности атомов Р ( r ), из которой следует парный потенциал взаимодействия ф ( r ) и вид функции энергии внедрения F ( с ).

• 2.    ПОСТРОЕНИЕ ПОТЕНЦИАЛА

Для рассмотрения электростатического взаимодействия атомов используют квазикласси-ческую модель, где заряд электронов считается «размазанным» вокруг ядра, и подбирают параметры плотности распределения заряда из сравнения с экспериментальными данными. Самый простой вид функции распределения зарядов – сферически симметричный. Исходя из решения уравнения Шредингера для водородоподобного атома и учитывая, что при расчете энергии взаимодействия двух атомов физически интересны большие расстояния между ними, т.е. внешние оболочки, авторами работ [5, 6] была предложена следующая аппроксимация плотности заряда электронного облака с учетом нормировки оя5              .

oCr) =------------------ fl + ВтУе ^ar

P йпСбар + 12£2 + a2) P где Q - заряд ядра атома, tt, P — подгонные параметры.

После интегрирования уравнения Пуассона, используя полученную зависимость плотности распределения заряда и учитывая энергии взаимодействия двух ядер друг с другом, их электронных оболочек и ядер с электронными оболочками другого атома, форма парной части взаимодействия имеет следующий вид

e yaQ2        v1

Функция внедрения F ( с ) задавалась в следующем виде

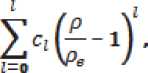
где Р e - равновесная электронная плотность, cl – коэффициенты, определяющиеся в процессе параметризации потенциала взаимодействия.

Таким образом, из трех подгонных параметров необходимо подобрать только а , P , а параметр У , как и коэффициенты энергии внедрения c_l будут определены, исходя из решения системы уравнения, состоящей из следующих уравнений:

равновесная электронная плотность рв = / pW.

£__। уравнение равновесия кристаллической решетки

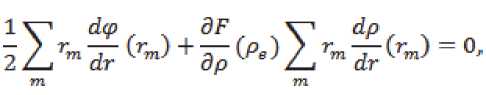
энергия связи на атом

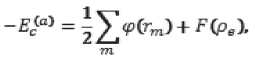
энергия образования вакансии

-Е^ = ^Д,»^* ^(Pel^PtTm)-- g^i (Pe^P ЧГтУ

значение модуля всестороннего сжатия

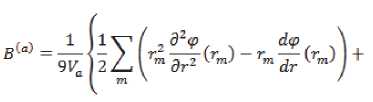
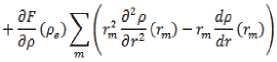
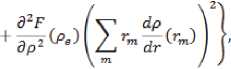
где V_a – атомный объем, r_m – расстояние от начала координат, которые связаны с одним из атомов идеального, однородного кристалла при нулевой температуре, до атома m .

Для различных пар значений ( P ) вычисляются значения ^р e , ^у , F ( ce ), F ( ^р e ), F ”( ^р e ), при которых выполняются следующие условия (Е_с - E_c^Y + (Е, - Е^)¹ + (В - B^Y = 0, у > 0.

dF           д'РРСРв'ХО,    — <А,)<0,    -=-?<Рв’>>0ор           ор

где E_c , E_v , B – экспериментальные значения энергии сублимации, энергии образования вакансии и модуля всестороннего сжатия.

Из полученного множества выбирается пара оптимальных значений ( а , P ), при которых величина

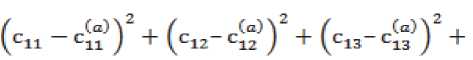
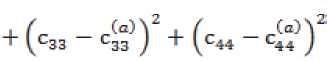
принимает минимальное значение, где c11, c12, c13, c33, c44 – экспериментальные значения упругих постоянных, c11(а), c12(а), c13(а), c33(а), c44(а) – вычисленные значения упругих постоянных.

Коэффициенты c_l функции вложенной энергии определяются из вычисленных значений р e ,

F ( с _e ), F’ ( с _e ), F’’ ( с _e ), условия F (0) = 0 и условия удовлетворения подобранного потенциала межатомного взаимодействия уравнению состояния Розе при 0.8 < а‘ <1.6 .

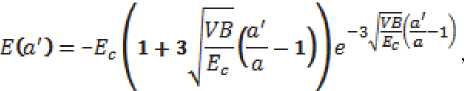
где B – модуль всестороннего сжатия, V – атомный объем, а – параметр идеальной кристаллической решетки, E _c – энергия сублимации (на один атом системы).

При параметризации учитывалось влияние только ближайших соседних атомов, расположенных на расстояние не более 2 c , где с – параметр ГПУ решетки.

• 3.    РЕЗУЛЬТАТ ПАРАМЕТРИЗАЦИИ ПОТЕНЦИАЛА ВЗАИМОДЕЙСТВИЯ

Значения физических величин, используемых для нахождения параметров а и Р для чистого бериллия, приведены в табл. 1.

Таблица 1. Значение физических величин бериллия

Физическая величи на	Зн ачен ие
? , А	2,2856
с , А	3,5831
Ec , эВ/атом	3,32
Ev , эВ	1,11
B , эВ/А3	0,7255
c11 , эВ/А3	1,8325
c12, эВ/А3	0,16 13
c13, эВ/А3	0,0874
c33, эВ/А3	2,2263
c44, эВ/А3	1,0373
Q , e	4

Вычисленные значения параметров парного потенциала взаимодействия и энергии внедрения

Таблица 2. Значение параметров потенциала бериллия

Параметр Зн ачен ие α, 1/А 1,307 β, 1/А -0,172 γ 0,5243 ρe, e/A3 0,23239 с0, эВ -5,25434 с1, эВ -3,04278 с2 , эВ 0,02463 с3, эВ -0,38497 с4, эВ 0,21 854 для чистого бериллия приведены в табл. 2.

В табл. 3 представлено сравнение экспериментальных и вычисленных значений упругих постоянных, энергии внедрения и энергии образования вакансии бериллия.

• 4.    ЗАКЛЮЧЕНИЕ

В работе были подобраны параметры потенциала межатомного взаимодействия чистого бериллия. Наблюдается хорошее соответствие между вычисленными и экспериментальными значениями различных физических параметров бериллия, за исключением значений упругих постоянных c12, c13, c44. Для более точного описания упругих постоянных возможно потребуется модификация аналитических выражений, описывающих потенциал. Однако, построенный потенциал межатомного взаимодействия можно использовать для моделирования процессов дефектообразования в бериллии под воздействием радиационного облучения и термических нагрузок.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг. и при частичной поддержке РФФИ – проекты 12-08-97076 и 13-01-00945

Таблица 3. Экспериментальные и вычисленные значения физических величин бериллия

Физиче ска я вели чина	Экспериментальные зна чен ия	Вычисленные зна чен ия
E c , эВ	3,32	3,32
Ev , эВ	1,11	1,11
B , эВ/А3	0,7255	0,7255
c11 , эВ/А3	1,8325	1,8098
c12, эВ/А3	0,1613	0,6132
c13, эВ/А3	0,0874	0,5530
c33, эВ/А3	2,2263	2,1659
c44, эВ/А3	1,0373	0,5983