Поддержание зоны покрытия спутниковой многолучевой гибридной зеркальной антенны при контроле текущего профиля рефлектора по сигналам наземного маяка

Спутники связи, реализующие технологию HTS (High Throughput Satellite), прочно вошли в состав глобальных сетей широкополосного доступа. Их разработка и совершенствование сопряжены с решением ряда сложных технических задач. В частности, для формирования игольчатых лучей в доли углового градуса используются крупногабаритные зеркальные антенны. Требования к точности ориентации лучей столь высоки, что приходится считаться даже с относительно малы-

ми искажениями профиля рефлектора, вызванными, например, изменчивостью солнечного теплового потока при вращении спутника вокруг Земли и вместе с ней. Искажение профиля рефлектора проявляется прежде всего в нарушении требуемой ориентации лучей наряду с некоторым изменением их формы и снижением коэффициента направленного действия (КНД).

Естественно, применяются конструктивные и технологические решения, повышающие жесткость и температурную стабильность рефлектора [1, 2]. Однако в случае зонтичных конструкций этих средств недостаточно и требуются адаптивно управляемые системы компенсации, как правило, включающие оптические каналы фотограмметрии, и |_ 0СМ1ЛЧЕСКИЕ АППАРАТЫ VI технологии к^нв голографических или лазерных измерений [3–7] для контроля текущего профиля рефлектора, и механические системы коррекции на основе многокоординатных приводов [1, 4, 5, 8–12]. По результатам измерений координат достаточного числа точек рефлектора [5, 13] вычисляется поверхность так называемого параболоида наилучшего соответствия (ПНС), или «Best-fit rotational paraboloid» в английской терминологии. Математическим и алгоритмическим вопросам реконструкции ПНС посвящен ряд работ [14–17]. Смещение оптической оси ПНС с номинального направления

• ¹⁸⁶ является наиболее опасным фактором. Поэтому двухкоординатный привод управляемого поворота рефлектора в узле крепления к несущей штанге [7, 18] выполняет основную роль механической системы юстировки спутниковой антенны на орбите. В дополнение к этому контроль положения концов спиц зонтичного рефлектора и система со-

• ответствующих оттяжек позволяют поддерживать не только требуемую ориентацию оптической оси, но в определенной мере и форму поверхности рефлектора [19].

В случае многолучевой гибридной зеркальной антенны (МГЗА) перспективной альтернативой механическим системам выступает электронная стабилизация лучей за счет адаптивного управления векторами весовых коэффициентов (ВВК) кластеров, формирующих лучи [2, 20, 21]. Причем становится возможным отказаться и от оптической системы контроля профиля рефлектора. Во-первых, сигналы, принимаемые элементами антенной решетки (АР) от наземного источника-маяка, образно говоря, несут в себе отпечаток рефлектора, и в принципе, позволяют судить о теку-

Том 8

щем состоянии рефлектора [22]. Во-вторых, благоприятная особенность состоит в том, что в силу малых искажений профиля рефлектора можно вычислить ПНС по сигнальному отпечатку на ограниченном числе элементов АР, в качестве которых может выступать широко применяемый на практике кластер гексагональной структуры из семи элементов. Таким образом, цель работы – исследование возможностей как контроля профиля рефлектора, так и стабилизации лучей спутниковой многолучевой гибридной зеркальной антенны электронными средствами.

1.    Рефлектор и его параболоид наилучшего соответствия 1.1.    Конфигурация МГЗА

Офсетная оптическая схема крупногабаритной спутниковой МГЗА предопределена тем, что АР размещена на корпусе аппарата, а рефлектор, как правило, зонтичного типа – на выдвижном кронштейне. Естественно, оптическая ось МГЗА ориентирована на центр рабочей области, а отклонение периферийных лучей при их ширине ≈ 0,8° в разы превышает это значение (для геостационарного спутника земной шар видится в угловом секторе ± 8°). В интересах поддержания параметров периферийных лучей на уровне центральных используют длиннофокусный рефлектор.

На рисунке 1 представлена МГЗА, геометрия которой повторяет российский проект «Рефлектор 2025» для покрытия территории РФ в L-диапазоне (частоты вблизи 2ГГц). Зеркало представляет собой вырезку из параболоида вращения с фокусным расстоянием F = 7,4 м, высекаемую цилин-

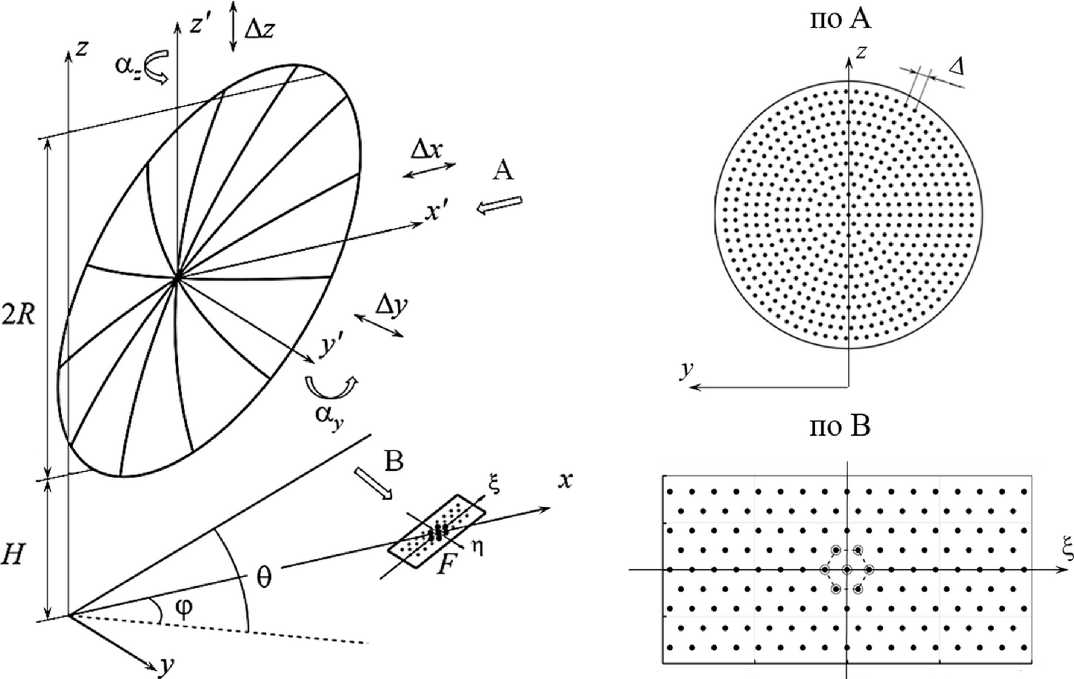
Рисунок 1. Геометрия МГЗА и используемые системы координат

дром радиуса R = 6 м, ось которого параллельна оптической оси 0x и смещена по оси 0z на расстояние ( R + H ) для обеспечения просвета-клиренса H = 3 м. Отказ от привычной привязки полярной оси z к оптической оси параболоида обусловлен тем, что у экватора координатные линии сферической системы хорошо сочетаются с прямоугольной конфигурацией рабочей области.

Конструктивно рефлектор состоит из двенадцати спиц-ребер необходимого профиля и натянутого на них сетеполотна из тонкой золоченой нити. Центральная зона рефлектора, обладающая большей жесткостью, служит местом крепления к выдвижной несущей штанге. Поэтому наряду с глобальной системой координат ( x , y , z ) полезно ввести параллельную ей систему отсчета ( x ′, y ′, z ′), привязанную к центру рефлектора, в которой описывать искажения рефлектора в виде малых поворотов на углы a z и a y вокруг осей z ‘ и у ‘ соответственно смещений Δ x , Δ y , Δ z вдоль одноименных осей и изменения фокусного расстояния на Δ F . При таком классе искажений гарантируется существование точного решения задачи реконструкции ПНС, что важно на этапе оценки эффективности и выбора подходящих численных алгоритмов.

Сохраняя габариты АР (1х2 м²) и ее гексагональную структуру с междуэлементным расстоянием в 0,8 ^, где ^ = 15 см, для большей универсальности получаемых оценок будем считать, что МГЗА формирует 51 луч, которые покрывают прямоугольную рабочую область ±3° по углу места θ и ±1,5° по азимуту φ. Соответственно, АР состоит из восьмидесяти четырех элементов, образующих пятьдесят один кластер гексагональной конфигурации, которые частично перекрываются. На рисунке 1 (вид B) выделен центральный кластер. Центр АР совмещен с фокусом параболоида, а ее плоскость наклонена под углом в о = 62° к оси 0х так, что нормаль ориентирована в центр рефлектора (рисунок 1). Оси ξ и η образуют локальную систему координат для полотна АР и ее элементов {ξ n , η n }.

В системе координат (x, у, z) произвольная точка номинальной поверхности рефлектора представляется радиус-вектором r = {( y2 + z2)/4 F; y; z }T. (1)

Здесь и в дальнейшем символ Т означает транспонирование. В локальной системе координат ( x ʹ, y ʹ, z ʹ) с учетом (1) точкам номинального рефлектора соответствует вектор r ’ = r - r₀ . Здесь

валентного ПНС смещается от центра АР в пределах сферы радиуса 83 мм. Будучи параболоидом вращения, ПНС однозначно определяется шестимерным вектором т = { A F ; a _z ; а y ; A x ; A y ; A z } отклонений его параметров от номинальных значений. Введем обозначения: d = { A x ; A y ; A z } для вектора смещения и Ψ для матрицы поворотов

T =

cos a _y cos a _z sinα _z

- sin a _z cosa _y cosα _z

- cos a _z sina _y

sinα _y sinα _z

sin a _y 0

cosa _y J

С учетом (1) и (2) равенство

r ( т ) = r₀ + Tr ' + d

задает точки ПНС с параметрами τ .

2                     T r, ={(H + R) /4F;0;H + R} есть радиус-вектор

центра номинального рефлектора.

В реальных условиях рефлектор испытывает небольшие искажения. Уровень этих искажений таков, что, по оценкам разработчиков, фокус экви-

1.2. Расчетная модель МГЗА

Широко применяемые среды электродинамического моделирования, такие как CST, FEKO, HFSS, реализуют достаточно строгие численные методы, позволяющие учесть краевые и поляризационные эффекты, взаимодействие элементов АР и т.п. При габаритах антенны порядка 100 λ, как это имеет место в рассматриваемом случае, расчет каждого луча длится десятки минут, что существенно ограничивает возможности многовариантных вычислений, необходимых, например, для вероятностных оценок эффективности стабилизации лучей. Это побуждает применять менее затратные алгоритмы приближенного моделирования крупногабаритных зеркал. Тем более что особенности рассматриваемой антенны благоприятствуют этому.

Во-первых, при длиннофокусной схеме кривизна рефлектора не велика, и отраженное поле имеет практически ту же поляризацию, что и облучающее поле. Поэтому и поля, и диаграммы направленности описываются скалярными функциями, относящимися к основной поляризации. Во-вторых, благодаря офсетной схеме и значительному просвету H , полотно АР не затеняет апертуру зеркала. Наконец, рабочая область МГЗА ограничена небольшим телесным углом у оптической оси. Всё это позволяет существенно упростить расчеты.

Следуя [20, 23], сигнал n -го элемента АР при облучении с направления (θ, φ) будем вычислять в простейшем варианте физической оптики как сумму сферических волн от достаточно большого числа P max точек рефлектора ( p = 1… P max ):

Sn ( т, 0,Ф ) = £ Ip ( т,0,ф ) f0 ( V n, p ) exp (— jkrp ) / rn, p,(4) p где Ip (т,0,ф) = exp(jkrp (т)• r0 (0,ф)) — это ток, наводимый падающей с направления (0, ф) плоской волной в p-ой точке ПНС, г0 (0,ф) = = {cos0cosф;cos0 sin ф; sin 0} - орт направления

U |_ ОСМИЧЕСКИЕ АППАРАТЫ VI

ТЕХНОЛОГА нш

(θ, φ), r_{p, n} – расстояние между p -точкой ПНС (3) и n- элементом решетки.

Диаграмма направленности (ДН) F (0, ф), соответствующая кластеру с ВВК { W_n }, находится как взвешенная сумма сигналов (4), т.е.

f ( е,ф ) = £ W n S n ( т ,е,ф ) ,

притом что угловые Координаты (0, ф) варьируются в ограниченных пределах.

В [23] подтверждена приемлемая точность расчета ДН по (5) и (4) в сравнении с ДН, рассчитанными в среде Ticra Grasp. Определенную роль 188 в обеспечении этой точности играет число Pmax точек и то, как они расположены на поверхности рефлектора. Естественно, использовать равномерно плотное распределение координат точек (yp′, zp′) в пределах круга радиуса R (рисунок 1, вид А). При выбранном дискрете Δ это реализуется в виде серии окружностей радиусов ρm с шагом, близким к Δ, на которых точки расположены с угловым дискретом dψm = trunс(2πρm/Δ), где функция trunс означает целую часть числа. Как показано в [16, 20], при рассматриваемых габаритах рефлектора достаточно Pmax = 150 точек.

2.    Алгоритм реконструкции параболоида наилучшего соответствия

В отличие от работ [5, 13, 16, 24], где ПНС аппроксимирует выборку контролируемых (так называемых реперных) точек рефлектора, в рассматриваемой постановке задачи под ПНС понимается параболоид с такими параметрами τ , при которых плоская волна от маяка с известного направления (0_О, ф₀) порождает на задействованном (на этапе реконструкции) кластере сигналы S ( τ ) = { S_n ( τ )} ( n = 1..7), максимально близкие к принятым в текущей ситуации сигналам S(°) = { S_n ^(o)}, т.е. сигнальному отпечатку от реального рефлектора. При этом ПНС выступает в роли не геометрического, а электродинамического эквивалента текущего профиля рефлектора.

Как меру отличия таких разнородных сигналов (вычисленных и измеренных) удобно исполь-

Том 8

зовать упомянутое выше значение «среднеквадратичного отклонения по форме» [25], которое дается выражением

*² ( т ) =¹ -| ( ^S ( т ) , ^{S ( 0 )} )|²/I I^s ( т )||²|||S ⁽ ' ^о)| [.        (6)

Здесь крупные скобки в числителе означают скалярное произведение комплекснозначных векторов. Реконструкция ПНС сводится к минимизации целевого функционала (6) по искомым параметрам τ. Решение этой задачи может быть найдено лишь численными методами, в частности градиентного спуска [26]. Тем более что могут быть получены хотя и громоздкие, но аналитические выражения градиента функционала (6). Как показывают статистические расчеты, для градиентного спуска в рассматриваемой задаче г-. ,“-..„ad.2 (г))         (7)

оптимальное значение скорости спуска достигается при значении шага h = 10^–3.

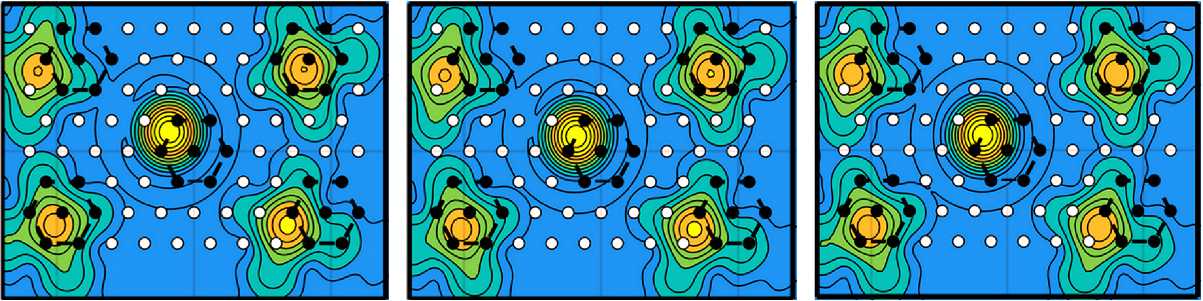
При всей кажущейся простоте задачи – по семи отсчетам найти шесть параметров - критическая особенность ее состоит в том, что при относительно малых значениях такие параметры, как A F и А х , a z и А у , а y и A z , вызывают весьма схожие изменения сигнального отпечатка. Например, по сигнальному отпечатку рефлектора, фокус которого смещен на 83 мм за счет одновременного поворота рефлектора вокруг осей z и y на 15ʹ, в результате градиентного спуска по (7) может реконструироваться ПНС № 1 с параметрами τ ₁ = {–0,46 мм; 10,74ʹ; 13,7ʹ; –1,72 мм; 3,57 мм; –13,84 мм} при ε₁ = –36,1 дБ, а может ПНС № 2 с параметрами т ₂ = {-34,56 мм; 1,06'; 1,69'; -37,08 мм; 45,67 мм; -36,72 мм} при с₂ = -26,7 дБ. В первом случае ПНС реконструировался преимущественно за счет поворотов (что корректно), во втором - за счет смещений вершины. В обеих ситуациях фокальные пятна, порождаемые каждым из этих ПНС, близки к пятнам от реального рефлектора, и в этом смысле оба ПНС эквивалентны реальному рефлектору. На рисунке 2 представлены амплитудные рельефы пяти фокальных пятен: при облучении из центра рабочей области (по которому осуществлялась ре-

абв

Рисунок 2. Амплитудные топограммы фокальных пятен: а – для искаженного рефлектора; б – для реконструированного ПНС № 1; в – для реконструированного ПНС № 2

конструкция ПНС) и при четырех периферийных направлениях облучения.

Несмотря на различие параметров моделируемого реального параболоида и реконструированных, структура фокальных пятен остается очень близкой. С физической точки зрения это объясняется возможностью электродинамической эквивалентности рефлекторов, не совпадающих геометрий наподобие того, как эквивалентны параболоиды с совпадающей точкой фокуса при отличающихся фокусных расстояниях. Формально же это проявляется в том, что рельеф целевой функции е²( т ) содержит плоские участки (плато), и процесс минимизации может завершаться в разных точках на этих плато.

3.    Дофокусировка МГЗА по ПНС

В соответствии с известным принципом формирования максимума ДН для формирования луча в m -ом направлении {θ _m , φ _m } весовые коэффициенты кластера W m должны быть пропорциональны комплексно-сопряженным значениям сигналов S _m от плоских волн, приходящих с направлений {θ _m , φ _m }. Для краткости сигналы S _m будем именовать фокальными пятнами. ВВК рассчитываются по номинальному профилю рефлектора т ₀, записываются в процессоре и воспроизводятся при обработке сигналов кластеров. При искаженном профиле рефлектора необходимо корректировать ВВК в соответствии с изменяющимися сигналами S m *, которые вычисляются по (4) после того, как найдены текущие значения параметров τ ПНС.

В функциональном отношении наиболее «вредным» искажением является отклонение оптической оси рефлектора от требуемого направления, поэтому за основу для оценки эффективности выбрано искажение τ_max = {0; 16ʹ; 22ʹ; 0; 0; 0}.

Вектор τ = γ τ_max масштабировался случайным параметром у в диапазоне от 0 до 1. Для оценки эффективности использовался минимаксный критерий, полученные зависимости представлены на рисунке 3. Здесь кривая 1 – минимальный средний уровень коэффициента усиления среди всех лучей системы (для каждого луча рассчитывается коэффициент усиления (КУ) в 130 точках, равномерно распределенных по круговой области диаметром 0,7° в плоскости углов θ и φ, с центром, совпадающим с номинальным положением луча; из полученных наборов берется среднее, затем минимум от средних значений при отсутствии адаптации ВВК, кривая 2 – аналогичный параметр при адаптации ВВК по ПНС, кривая 3 - при адаптации ВВК по рефлектору.

На рисунке 3 кривые 2 и 3 совпадают в пределах графической точности, что говорит об одинаковой эффективности адаптации ВВК как при расчете по ПНС, так и по рефлектору, если бы его профиль был известен. Соответствующие значения отличаются в 3-м знаке, естественно, в пользу адаптации ВВК по рефлектору.

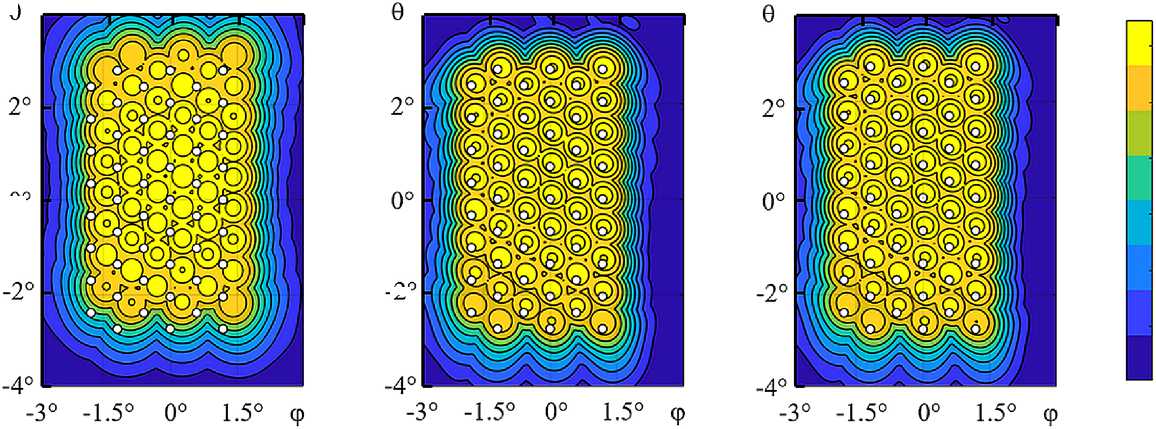
На рисунке 4 и рисунке 5 ( а – в ) для примера приведены топограммы лучей. Слева - топограм-ма лучей без коррекции ВВК, в середине - с коррекцией ВВК по реконструированному ПНС, справа - с оптимальной коррекцией ВВК по профилю рефлектора, как если бы он был известен. Белыми точками обозначены номинальные положения лучей. Моделировались два характерных варианта искажений. В первом случае (рисунок 4) моделировалось искажение профиля, соответствующее повороту (относительно локальных осей координат, привязанных к вершине параболоида) рефлектора на α _zy = 15ʹ от номинального положения.

На рисунке 5 представлены аналогичные результаты для случая, когда искажения рефлек-

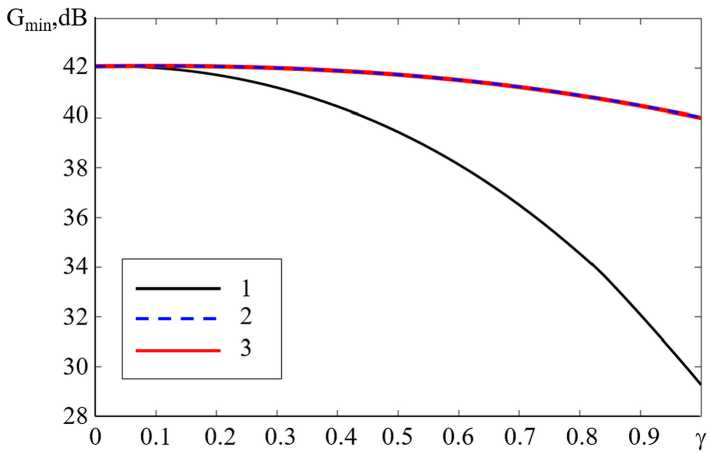
Рисунок 3. Минимальный средний коэффициент усиления во всех зонах обслуживания:

1 – без коррекции ВВК; 2 – с коррекцией ВВК по ПНС;

3 – с коррекцией ВВК по фактическому профилю рефлектора

If I — ОСМИНЕСКИЕ АППАРАТЫ VI ТЕХНОЛОГИЙ иен

Том 8

A

-2°

G, dB

б

а

в

Рисунок 4. Топограммы лучей МГЗА: а – без коррекции ВВК; б – с коррекцией по ПНС; в – с коррекцией по рефлектору; г – цветовая шкала к рисункам а-в

0°

-3° -1.5° 0° 1.5° ср -3° -1.5° 0° 1.5° ср -3° -1.5° 0° 1.5° ср а  бв

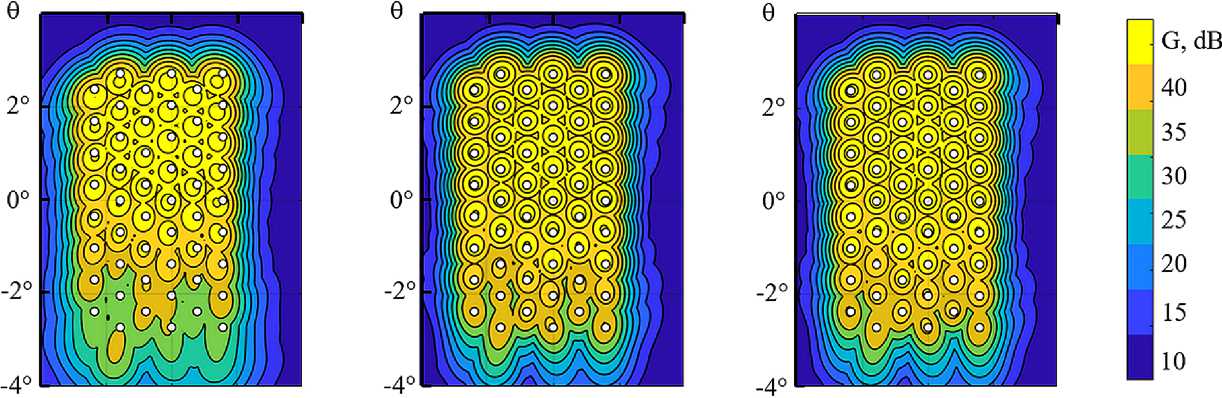
Рисунок 5. Топограммы лучей МГЗА: а – без коррекции ВВК; б – с коррекцией по ПНС; в – с коррекцией по рефлектору; г – цветовая шкала к рисункам а-в

тора не сводятся к параллельным смещениям и угловым отклонениям, а затрагивают его форму в виде «козырькового» отклонения профиля рефлектора по оси 0 х , что соответствует формуле x ( y , z ) = ( у ² + z ² ) / 4 F + d sin² ( п ( z - H - R ) / 4 R ) с максимальным отклонением d = 70 мм у верхнего края зеркала. Направление на маяк совпадало с оптической осью МГЗА (0_О = 0°, ф₀ = 0°). Расчеты сигнального отпечатка S⁽⁽⁰⁾ и ДН лучей МГЗА выполнялись в среде CST Studio Suite методом интегральных уравнений. Причем АР состояла из турникетных облучателей, соответствующим питанием которых обеспечивалась круговая поляризация.

Как видно из левых топограмм на рисунках 4 и 5, в ситуации без дофокусировки лучи смещены и коэффициент усиления в центрах их локальных зон заметно снизился. Средние и правые то-пограммы подтверждают существенный эффект в восстановлении как ориентации лучей, так и их коэффициентов усиления. Кроме того, эффект от дофокусировки по ПНС близок к предельно возможному эффекту при оптимальной дофокуси-ровке по реальному рефлектору.

4.    О принципе формирования луча в заданном направлении

Формирование максимума ДН возбуждением элементов АР пропорционально комплексно-сопряженным значениям f n * (0 m , ф m ) их ДН в желаемом направлении {0 m , ф m } настолько органично по физике (синфазное сложение полей в этом направлении и малые траты мощности на элементы, слабо туда излучающие), что как само собой разумеющееся этот принцип не может не быть известным. Однако оказались безуспешными попытки найти в учебниках по антеннам (А. А. Пистолькорса, А. З. Фрадина, О. Г. Вендика, Д. М. Сазонова, Д. И. Воскресенского), включая фундаментальный труд Баланиса К. А. «Теория антенн: анализ и проектирование», хотя бы на уровне формулы упоминание такого подхода. Поскольку этот принцип положен в основу предлагаемой электронной адаптации лучей спутниковой ГЗА к эксплуатационным искажениям рефлектора, то считаем оправданным изложить этот принцип углубленно.

В случае АР из большого числа элементов, индивидуальные ДН которых слабо направлены, формирование луча в желаемом направлении (00, ф0) достигается за счет фазирования, обеспечивающего синфазное сложение полей в этом направлении. Соответствующий прием составляет суть электронного сканирования и детально исследован применительно к линейным, плоским и выпуклым АР. Ситуация с МГЗА иная: крупногабаритный рефлектор, облучаемый элементами АР, создает набор узких индивидуальных лучей, ориентация которых зависит от положения соответствующего элемента на антенном полотне. Формирование луча, покрывающего локальный участок рабочей зоны кластером элементов вместо одиночного, позволяет повысить КУ в пределах этого участка и снизить уровень бокового излучения в пользу развязки между каналами. Естественно, возникает вопрос об оптимальном возбуждении кластеров.

Не усложняя анализ, будем считать, что поляризация полей всех элементов АР одинакова, и ДН, соответствующая вектору W весовых коэффициентов { W_n } некоторого кластера (здесь n ‒ индекс элементов кластера), описывается простейшим и в то же время универсальным равенством

F (в, Ф»С n W n f (в, Ф). (8)

Здесь fn(0, ф) - это ненормированная индивидуальная ДН n-го элемента в единой глобальной системе координат, которая для элемента, расположенного в точке (xn, yn, zn), определяется следующим образом fn (в,Ф) = en (0, Ф) exp(j k(xn sin0 cosФ + + yn sin0 sinф + zn cos0)),

где e n (0, ф) - комплекснозначная функция, описывающая поле n -го элемента в дальней зоне при единичной амплитуде его возбуждения и начале координат, совмещенном с точкой ( x_n , y_n , z_n ) расположения n -го элемента. Отсутствие нормировки индивидуальных ДН, приводящей к учету энергетических потерь, свойственных конкретному элементу, или выигрыша за счет коэффициента усиления (направленность плюс КПД) - играет важную смысловую роль в критерии оптимальности луча, сформированного АР.

По здравому смыслу эвристический прием формирования луча в заданном направлении (00, ф0) сводится к несложной догадке: зададим-ка ВКК равным комплексно-сопряженным значениям индивидуальных ДН в направлении максимума { Wn =fn* (00, ф0)}. Во-первых, в этом направлении поля от всех элементов АР будут складываться в фазе: F(6o, Фо) = Znfn Ч, Фо) fn (00, Фо) =Z n\fn (00, Фо) |2 . Во-вторых, если какой-то элемент не излучает в этом направлении или излучает слабо, то и не следует на него расходовать подводимую мощность. Рациональность такого подхода не вызывает сомнения, но остается открытым вопрос, являет- ся ли это решение в каком-либо смысле оптимальным.

Аналогия с оптимальной фильтрацией. ДН линейного излучателя F (0) есть Фурье преобразование от амплитудно-фазового распределения (АФР) W ( x ) точно так же, как временная зависимость s ( t ) сигнала связана с его спектром S(ra). Известно, что максимально возможное отношение сигнал/шум на выходе фильтра обеспечивается при оптимальной частотной характеристике K_opt(ω), которая повторяет комплексносопряженный спектр сигнала K_opt(ra) = S * (ra). При этом мощность шума на выходе Р_ш = п_ш ||K_opt(ra)||² есть произведение его спектральной плотности п_ш и квадрата нормы частотной характеристики фильтра. Эти результаты трансформируются в ситуацию с линейной антенной заменой s(t) на F (0) и К(ю) на W ( x ). Теперь выходом пространственного фильтра служит «точка» 0_О дальней зоны, а коэффициентами передачи К(ю) спектральных составляющих на выход фильтра теперь являются коэффициенты передачи от элементов x к «выходу антенны» 0 0 , т.е. значения f ( x , 0 0 ) индивидуальных ДН. Ясно, что в антенном случае задача инверсная: задан «фильтр» f ( x , 0₀) и следует найти тот «сигнал» W( x ), который обеспечит результат, оптимальный в вышеуказанном смысле. Сути дела это не меняет и в антенной нотации приводит к равенству W ( x ) = f * ( x , 0 0 ).

Очевидно, что АР произвольной конфигурации аналогична ситуации с сигналом линейчатого спектра S(ra _n ), и это соотношение трансформируется в обобщенное АФР

{W n = f n *(0 о , Ф о )}. (10)

При этом ясно, что исходный критерий оптимальности этого решения (максимум отношения сигнал/шум) теперь означает максимум интенсивности поля в направлении 0₀ при ограниченной норме АФР || W ||². Если бы квадрат нормы АФР был пропорционален подводимой мощности, то решение (10) соответствовало бы максимальному коэффициенту направленного действия в направлении (0₀, ф₀). Но электродинамическое взаимодействие элементов АР изменяет их входные сопротивления, и потому сформулированное выше толкование критерия оптимальности решения (10) не строгое, вполне приемлемое, если шаг решетки не слишком мал. Представляют интерес количественные оценки отклонения решения (10) от строгого решения на максимум КНД.

Оптимальное решение. Поиск АФР, соответствующего максимуму КНД в требуемом направлении, составляет суть синтеза антенны по ДН в виде δ-функции. Давно [25, 27] показано, что если равенство (8) воспринимать как оператор, отображающий пространство АФР { W } в пространство реализуемых ДН { F (0, ф)}, то сопря-

I/ - J — 0СМ1ЛМЕ АППАРАТЫ VI ТЕХНОЛОГА иен женный ему оператор осуществляет обратное преобразование по правилу

W ( x ) = f _{4 n} F^, Ф) f * ( x ,e, 9)d Q ,

где Fо(0, ф) - синтезируемая ДН. Для заданной ДН F0(0, ф) в виде двухмерной 5-функции 5(0 - 0о, ф - ф0) и антенны в виде решетки выражение (11) с очевидностью превращается в {Wn = fn* (0о, ф0)}, т.е. совпадает с (10). Решение (11), не являясь предельно точным, обладает рядом привлекательных качеств [27]. В частности, среди всех решений с одинаковой точностью о2 = ||F(0, ф) - F0(0, ф)||2 мини-192 мальна его реактивность Q = || W(x )||2 / || F(0, ф)||2, характеризующая чувствительность ДН F(0, ф) к случайным погрешностям реализации АФР W(x) и к изменению частоты (узкополосность антенны). И это в дополнение к отмеченной выше энергетической эффективности, если ||W(x)||2 может вос- приниматься как подводимая к антенне мощность.

Ясно, что в отсутствии потерь (при КПД антенны 100 %) подводимая мощность совпадает с мощностью излучения, которая характеризуется квадратом нормы ДН || F (0, ф)||², а не квадратом нормы АФР || W ( x )||². В случае антенной решетки, как отмечалось выше, с ростом шага δ x ослабевает электродинамическое взаимодействие ее элементов и значение || W ( x )||² все точнее характеризует подводимую мощность. На примере линейной антенной решетки оценим отличие КНД, свойственного решению (10), от максимально возможного КНД.

Будем считать, что линейная АР состоит из N элементов длиной 5x, вплотную примыкающих друг к другу, имитирующих гипотетические конструкции с равномерным и синфазным амплитудно-фазовым распределением. Тем самым индивидуальная ДН n-го элемента соответствует выражению fn(0) = sinc(0.5в5xcos0) exp(jexn cos0), (12)

Том 8

где в = 2n/Z - волновое число, угол 0 отсчитывается от оси 0 x решетки, а sinc(x) обозначает функцию sin(x)/x. Задача наилучшего среднеквадратичного приближения линейной комбинации ^ n W n f n (e) известных функций f n (0) к требуемой ДН F ₀ = 5(0 - 0₀) сводится к системе линейных уравнений, решение которой и есть АФР, обеспечивающее максимальный КНД в направлении 0_о. На рисунке 6 представлены расчетные результаты.

Как обычно, КНД есть отношение G = | F (0_о)|²/|| F (0)||², а мерилом реактивности АФР выступает отношение Q = || W ||²/||F(0)||² - чем меньше излучаемая мощность при единичной норме АФР, тем хуже, реактивнее АФР. Ясно, что в решетке с плотным расположением элементов (малым волновым размером δ x /λ) наряду с хорошо излучающими АФР существуют реактивные, плохо излучающие АФР (с противофазно возбужденными соседними элементами). В точном решении присутствуют и реактивные составляющие в той мере, насколько они могут повысить КНД. В решении (10), благодаря свойствам сопряженного оператора (11), реактивные составляющие присутствуют с весами, обратными их реактивности [25], что и обеспечивает энергетическую оптимальность решения.

Как видно из графиков, выигрыш в КНД при замене решения (10) на точное решение невелик. По графикам его трудно определить, а расчеты показывают, что в приведенных ситуациях максимальное различие кривых G(δ x /λ) составляет: а) 0.18, б) 0.231, в) 0.225. По мере увеличения шага решетки оно сокращается и при 5 x >  0.5 Z приближенное решение практически не уступает точному. В то же время для АР с малым шагом указанный скромный выигрыш по КНД оплачивается почти двукратным ростом реактивности. Наконец заметим, что на первый взгляд неожиданное (ведь раз-

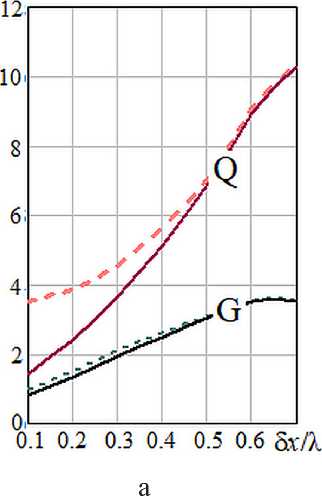
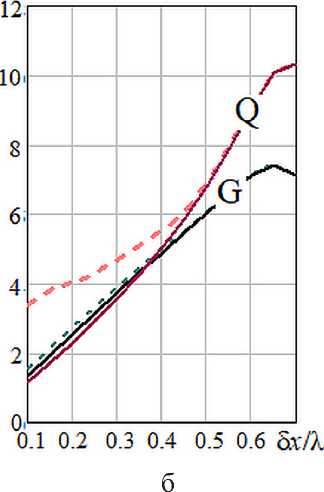
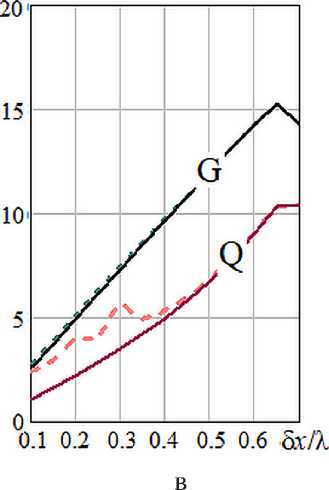
Рисунок 6. Зависимости КНД (G) и реактивности (Q) сопоставляемых решений (приближенное ‒ сплошная линия, точное ‒ пунктир) от шага δx антенной решетки и числа N ее элементов: а – N=6; б – N=12; в – N=24

мер АР увеличивается) замедление роста и спад КНД при 5 x > 0.65 X связаны с тем, что при отклоненном от нормали луче (было задано 0_О = 60°) в область видимых углов входит интерференционный максимум, что и снижает КНД.

Итак, расчеты подтверждают, что не требующий вычислительных затрат принцип комплексного сопряжения значений индивидуальных ДН в заданном направлении обеспечивает близкое к предельно возможному значению КНД.

Заключение

Отметим два момента, отражающих особенность проблемы электронной стабилизации лучей МГЗА при искажениях профиля рефлектора в условиях эксплуатационных нагрузок, стабилизации с реконструкцией ПНС по сигнальному отпечатку от наземного маяка.

Во-первых, естественно, максимально точное соответствие ПНС текущему профилю рефлектора желательно, однако решающим фактором является электродинамическая эквивалентность ПНС и рефлектора, что предоставляет некую степень свободы в вычислительном плане.

Во-вторых, указанные выше пары параметров ПНС (малые угловые повороты и параллельные смещения) коррелированы между собой в том смысле, что вызывают схожие изменения в сигнальных отпечатках. Поэтому число варьируемых параметров ПНС может быть сокращено в интересах ускорения вычислений и сокращения нагрузки на процессор канала стабилизации.

Статистические оценки эффективности электронной стабилизации лучей МГЗА в зависимости от уровня деформаций и алгоритмов реконструкции ПНС, включая сокращение числа параметров, могут стать предметом дальнейших исследований.