Подъем воды в ксилеме растений с трахеидальной проводимостью

Введение. Наличие вертикального восходящего потока воды в ксилеме растений объясняется действием силы поверхностного натяжения воды в менисках капилляров [1]. При объяснении подъема воды в капилляре радиуса r на высоту h традиционно рассматривают погруженный в воду стеклянный вертикальный капилляр и записывают условие равенства двух сил:

— силы, обусловленной весом столба воды в капилляре Р, направленной вертикально вниз,

—силы поверхностного натяжения воды в мениске капилляра F н, направленной вверх.

Уравнение равновесия этих сил для цилиндрического капилляра записывается в виде

Р = F н ^ 71 r ² h р g = 2 71 r а cos а,                                           (1)

где р , g , а,о— соответственно плотность воды, ускорение свободного падения, угол смачивания и коэффициент поверхностного натяжения воды.

Процессы и машины агроинженерных систем

Из (1) следует известная формула Жюрена, позволяющая определить высоту подъема воды в вертикальном :

ъ 2cycosct h Ж — ------.

г ру

.

Следует отметить, что применение формулы (2) для оценки высоты подъема воды в капиллярной системе древесных растений не позволяет учитывать силу сопротивления движению воды, обусловленную анатомическим строением капиллярной сети ксилемы . Кроме того, не принимается во внимание и сила, обусловленная осмотическим потенциалом корневой системы и приводящая к появлению действующего в сторону F и корневого давления /2_кор. Согласно [3, 4] его величина для растений средней полосы при оптимальных условиях составляет 0,15 МПа. Капилляр ксилемы, по которому поднимается вода, например, у хвойных деревьев состоит из связанных посредством пор трахеид. В отличие от хвойных, ксилема лиственных деревьев состоит из сосудов, связанных между собой имеющимися на их поверхности многочисленными порами. Существуют также ксилемы смешанного типа — трахеидально-сосудистые. Поив этом случае связь между элементами таких ксилем осуществляется посредством пор.

С учетом вышеизложенного соотношение (1) может быть записано следующим образом:

Р + F СП = F _н+ F кор "^ 71 r ² h р g + F СП = 2 кr□ cos а + тг r ² /?кор ,

где F СП =    i — суммарная сила сопротивления движению воды, обусловленная гидравлическими потерями напора при ее движении через сложную капиллярную структуру, содержащую N пор ; Ркор — корневое давление.

В литературных источниках отсутствуют сведения о гидравлических потерях напора при движении воды как через одиночную пору, так и через их совокупность.

Среди большого разнообразия видов пор растений [5] наиболее полно изучены и описаны геометрические размеры и строение округлых окаймленных пор с торусом. Они представляют собой высокоэффективный водопроводящий элемент. В структуре ксилемы хвойных деревьев трахеиды с окаймленными порами составляют 90–95 % от общего объема древесины. . Окаймленные поры расположены преимущественно на радиальных стенках у концов трахеид, которыми каждая трахеида вклинивается между соседними, образуя плотное соединение. Поры в стенках двух смежных трахеид располагаются одна против другой, образуя пару. На радиальной стенке трахеиды может находиться до 90 окаймленных пор, которые участвуют в проведении воды.

Цель работы. Расчет гидравлических потерь, возникающих при движении воды в ксилеме деревьев через одиночную окаймленную пору с торусом и через их совокупность, а также оценка влияния этих потерь на величину высоты подъема воды в капиллярах ксилемы.

Основная часть. На рис. 1 представлена модель участка трахеиды с внутренним диаметром D =2 R _т, которая имеет на противоположных радиальных стенках по одной одинаковой окаймленной поре с округлым отверстием.

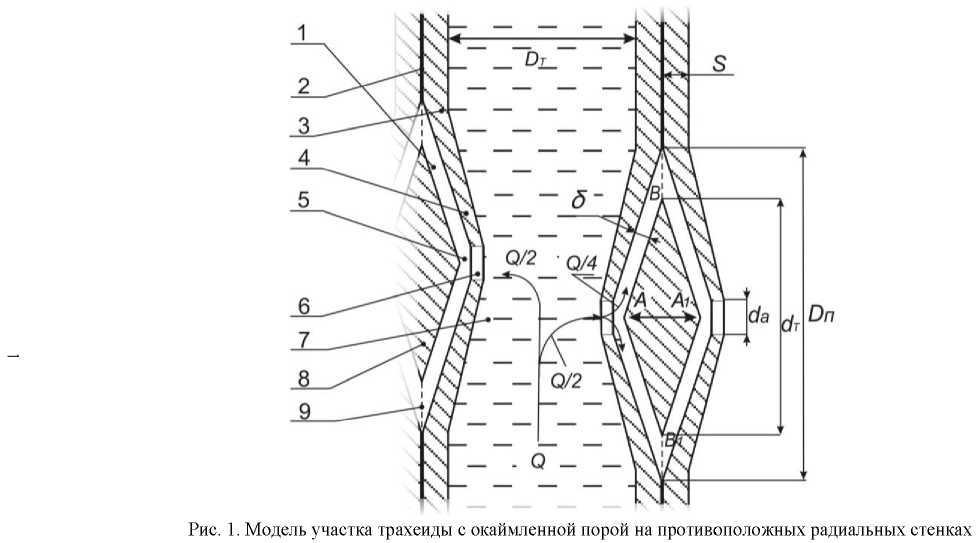
Окаймленные поры, образующиеся в стенках трахеид и сосудов, характеризуются тем, что полость поры сужается в направлении от замыкающей пленки к внутреннему отверстию поры. В окаймленной поре можно различить воронковидный поровый канал (1), расширяющийся по направлению к замыкающей пленке (2). Вторичная стен-118 ка 3 нависает в виде валика (4) над расширенной частью канала и образует камеру поры (5). Канал сообщается внеш- ним отверстием с камерой поры, а внутренним (апертура поры) (6) — с полостью (7) самой трахеиды. Это хорошо видно на фотографиях, выполненных с помощью оптического и электронного микроскопов [6]. Срединная часть замыкающей пленки окаймленной поры имеет чечевицеобразное утолщение, называемое торусом (8). Торус соединен с замыкающей пленкой тонкими нитями (9). Между ними нет никакой перепонки. Поэтому часть замыкающей пленки поры, на которой подвешен торус , не является сплошной перегородкой и не создает препятствия при движении воды.

У ранних трахеид средний радиальный размер составляет для лиственных и хвойных пород соответственно 52·10–6 и 40-10–6 м, а ^ поздних — 22·10–6 и 20-10–6 м. Тангенциальный размер в обоих случаях примерно 30 10–6 м [7].

Диаметр окаймленных пор D _пколеблется от 8·10^–6до 31-10–6 м, а диаметр входного и выходного отверстий в порах d _а (апертура) — от 4-10–6 до 8-10–6 м. Диаметр торуса ( d ) всегда больше d _а. Численные данные о соотношении диаметра торуса, диаметра поры и максимальной его толщинs (А4 1, см. рис. 1) в литературных источниках не приводятся. Толщина вторичной стенки поры s может достигать 1010–6 м.

Для определенности положим, что пора симметрична относительно вертикали и горизонтали и зазор б (поровый канал) между торусом и стенкой поры одинаков на всем пути движения воды. При этом максимальная толщина торуса равна 1010–6 м— толщине вторичной клеточной стенки. Тогда пути ЛВЛ 1 = АВ 1 4 1 = l , проходимые водой внутри поры в указанных выше пределах диапазона диаметров D п, одинаковы и находятся в следующем интервале: 5·10^–6< l <30-10 –6 м.

В силу одинаковости пор общий поток воды Q , передаваемый из трахеиды к смежным с ней трахеидам, делится пополам, и в каждую пору поступает объем воды, равный Q /2. В поровой камере вода обтекает торус восходящим и нисходящим потоками, каждый из которых имеет объем q = Q /4.

Объем Q зависит от скорости подъема воды в растении V, величина которой варьируется в широких пределах и зависит от вида растения, времени суток и сезона. В [8] представлены значения скоростей подъема воды в ксилеме растений. Большинство из них — в пределах от 1 до 10 м/ч. В [9] приводятся данные, согласно которым максимальная скорость движения воды в хвойных растениях — 1,2 м/ч, в лиственных значительно выше, а в дубе — 27–40 м/ч.

Для определения величины потерь гидравлического напора воды при прохождении ее через окаймленную пору с торусом воспользуемся формулой Пуазейля, описывающей закономерность течения вязкой несжимаемой жидкости в тонкой цилиндрической капиллярной трубке [10]:

q = к d ⁴ ( p 1 — p2 ) / (128 l ц),

где q — секундный объемный расход воды,м³ /с; p 1 – p 2 = Др — перепад давления на входе и выходе из окаймленной поры, Па; d — диаметр капилляра, м; р — коэффициент динамичеcкой вязкости воды, Па с ; l — длина капилляра, м.

Из (4) следует:

p 1 – p 2 = Др = 128 l Б q / (л d ⁴)                                            (5)

Величину d в (5) выберем, исходя из следующих соображений. Поступающая через апертуру в пору вода движется на участке ВАВ 1 вдоль конического зазора. При этом по мере ее продвижения количество воды, приходящееся на единицу площади поперечного сечения зазора, уменьшается — следовательно, уменьшается скорость ее движения и гидравлические потери. Но на участке ВА 1 в 1 коническое расширение сменяется уменьшением площади сечения зазора. Это приводит к увеличению скорости движения воды и усилению гидравлического сопротивления. В результате в силу симметрии гидравлические потери будут определяться только величиной пути, по которому движется в зазоре вода. Поэтому движение воды в зазоре можно рассматривать как происходящее в капилляре длиной l при d = б.

Исходя из возможных соотношений D п и d ,зададим диапазон изменения б: 2·10^–6<5<8·10^–6м. Примем диапазон изменения V : 0,28·10^–3< V <2,2-10 –3 м/с.

В табл. 1 приведены величины объема воды q = Q /4 ( Q = тс Ry V /4), проходящей за секунду через зазор б по пути АВА 1 между поверхностью торуса и внутренней поверхностью вторичной стенки окаймленной поры. При этом диаметры трахеид D т равны 2010–6, 30'10–6 и 40-10–6 м, и вода проходит через смежные стенки трахеид с разным количеством пор N . В каждом случае скорость подъема воды в ксилеме V — 1, 4 и 8 м/ч. Можно видеть, что объем воды, проходящей через одиночную пору в течение секунды, уменьшается прямо пропорционально N и увеличивается прямо пропорционально V .

Процессы и машины агроинженерных систем

Таблица 1

Объем воды, протекающей в секунду через зазор между торосом и поверхностью окаймленной поры

D Т-106, м	V ■ 10 3, м/с	q 1013, м3/с                                          I
		N
		1	10	25	50
20	0,28	0,22	0,022	0,0088	0,0044
	1,10	0,87	0,087	0,0348	0,0174
	2,20	1,74	0,174	0,0697	0,0350
30	0,28	0,50	0,050	0,0198	0,0100
	1,10	1,96	0,196	0,0780	0,0390
	2,20	3,90	0,390	0,1550	0,0770
40	0,28	0,87	0,087	0,0350	0,0178
	1,10	3,50	0,350	0,1390	0,0700
	2,20	7,00	0,700	0,2790	0,1400

На рис . 2 приведены рассчитанные по формуле (5) величины потерь давления Лр_МИн во время прохождения водой окаймленной поры при минимальных значениях величин V vIHH = – 3 м/с, N vIHH = 1, l МИН = – 6 М И §мин = –6 м, принятых в рассматриваемой нами модели . Диаметры трахеид —20-10–6 , 30-10–6и 40-10–6 м. Из рисунка следует, что при прохождении воды через одиночную пору с 5_МИН = –6 м величина Др^мин возрастает при увеличении диаметра трахеиды.

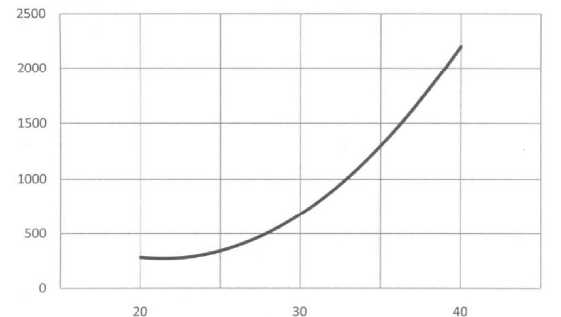
Армин, Па

Рис. 2. Зависимость Армия от диаметра трахеиды D г D г-10-6 , М

На основании (5) могут быть определены величины Др для других значений указанных выше величин по еле-

дующим соотношениям.

Увеличение l приводит к увеличению потерь давления, то есть

=

МИН Др мин

Увеличение количества окаймленных пор, участвующих в проведении воды, приводит к уменьшению потерь

давления, а именно

=

Л/мин Др ,

Увеличение скорости продвижения воды в трахеидах ксилемы увеличивает потери давления, что описывается

соотношением

=

.

,

6 бмин

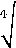
Ар

Ар мин

С учетом данных табл. 1 и рис. 2 по соотношениям (б)-(9) проведены расчеты величины диапазона изменения Ар. При этом рассматриваются изменения l в пределах 5•IO ⁶<  l < 30-10 ⁶ м и V , 8 — в пределах 0,28•IO ³ < V < 2,210^-3 м/с и 2 10^-6< 8 < 8-10^-6 м.

В табл. 2. представлены результаты расчета для трахеид диаметрами DT, равными 20-10 6 м и 40-10 6 м. При N =            (N = воду пор на стенке трахеиды.

Таблица 2

Потери давления при прохождении водой окаймленной поры

N	D T -106,м	01(0 м/с	6	Интервал изменения Ар, Па при 5-10 6<  l < 30- Ю 6м
1	20	0,28	2	281  1690
			8	1,1 - 6,6
		2,2	2	2220  13340
			8	8,7 52
	40	0,28	2	2200 - 13200
			8	4,4
		2,2	2	8940 - 53200
			8	35
50	20	0,28	2	5,6
			8	0,02 - 1,3
		2,2	2	45
			8	0,17
	40	0,28	2	22
			8	0,09
		2,2-103	2	179
			8	0,7

. 2, N = 1,                                             l , V D .

пых условиях приводит к уменьшению Ар. Абсолютная величина Ар в пределах рассматриваемого изменения пара-

1,1                                                                  N ,

N = 1.

При увеличении количества пор на стенке трахеиды до 50 Ар значительно уменьшается и варьируется в пределах от 0,02 до 1080 Па.

Как было отмечено выше, движение воды в коническом зазоре окаймленной поры в силу симметрии физиче-l принять за положительное направление действующих сил в сторону силы поверхностного натяжения, то для участков

,       1,       1, 1 1

• 3,    ):

Fpn = -ДР sin (90 - ) + ДР sin (90 - ) + ДР sin (90 - ) - ДР sin (90 - ) = 0.(10)

F,

Ситуация изменяется при отсутствии симметрии. Если повернуть оси по часовой стрелке на угол у/2, то сто

• 1         13, ).

,11

ложенными под углом у к горизонтали. Тогда для равнодействующей силы на выходе воды из поры можно записать

:

Fpn = -ДР sin (90 - у) + ДР + ДР - ДР sin (90 - у) = 2 ДР (1 - sin (90 - у ))^0.(11)

Процессы и машины агроинженерных систем

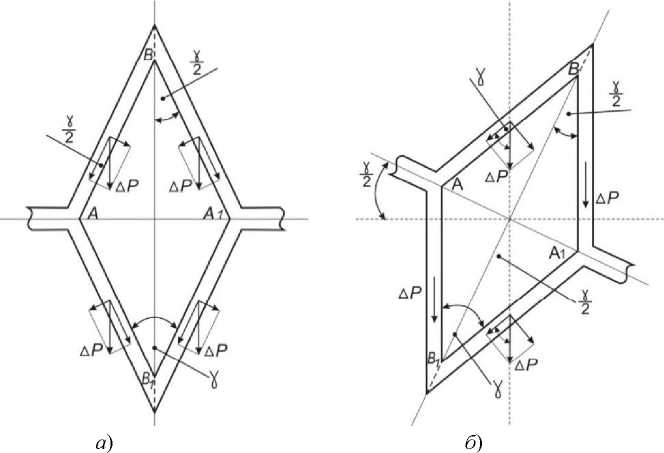
Рис. 3. Распределение сил в зазоре окаймленной поры, вертикально ориентированной (а) и наклоненной под углом к вертикали (б)

Трахеида не является вертикальным цилиндром, а клиновидно сужается радиальными стенками к концам, одной третью поверхности соприкасаясь с клиновидными поверхностями концов трахеид следующих уровней [7]. Поэтому вертикальная ось симметрии поры может быть наклонена. Угол у клина на конце трахеиды лежит в пределах 17-22 градусов. Величина F _pn в одиночной поре в зависимости от у может принимать значения в пределах:

F _pn = (0,015 - 0,035) ДР = (0,015 - 0,035) л8²р g l /8 = (0,002 - 0,0044) л8² p g l                 (12)

Тогда при минимальном и максимальном количестве трахеид на одном погонном метре величина F _pn соответственно равна:

(0,33 -^ 9) л:8² p g l и (8 -^ 19) л8² p g l.

С учетом вышеизложенного уравнение (3) может быть записано в виде

Р + F en — F pn = F _H + F _Kop ^ л г ² hpg + F _cn - F _plI = 2л r a cos a + л г ² /?_кор.

Подставляя в (13) аналитические соотношения для величин F _cn = л Ry Ар и F _pn из (11) и полагая, что в стволах деревьев хвойных пород длина трахеид A h находится в диапазоне от 2,5-Ю ^Зм до 5-10"³м [7], получим:

к Ry hpg + 32 к Ry -^ l ц V / N 84 — ^л8² p g l (1 — sin (90 — у) =2л Ry a cos a + uRy p^-           (14)

Сокращая (14) на л Rypg и учитывая (2), получим

32й£игИ    l 6²(1—sin(90 —у)) '

AhW54pg        ДНЯ^ ,

2ocos ct pg Ry

pg

pg'

Отсюда h = (h« + E™) / (1 + pg

32fl£UrH _ Z6²(l-sin(90-y))

AhW54pg       ДНЯ^

Уравнение (16) позволяет определить высоту подъема воды в капилляре ксилемы, состоящей из вертикальной цепочки трахеид, с учетом анатомического строения окаймленных пор.

Используя уравнения (13) и (14), можно выяснить степень участия корневого давления в подъеме воды в ксилеме. Для этого составим отношение сил:

F cn / F _KOp = 32 л R^ l ц V / N S⁴ kR^ р_юр = 32 Ry h l p V / Ah N S⁴ p^.                   (17)

Если F _cп/ F _KOp = 1, то вода под действием силы F _H поднимается на высоту h _ж, так как корневое давление компенсирует гидравлические потери при движении воды через поры.

При F cn / F _Kop<  1 корневое давление способствует подъему воды, и она поднимается на высоту, большую h _ж. ^22 При F _cn / F _Kop >  1 часть F _H расходуется на преодоление F _cп, и вода не может достичь h _ж.

Записав (17) в виде

,            ДН54..

— Д^КОр 7 ,

¹ 32Rf I цУ

= 0,15

Так, h < 1,34 N при RT =10-10-6 м, l = 5-Ю-6 м, ц = 1,002-10-3 Пас, V = 0,28-10-3 м/с, 8 = 2-Ю-6 м, hh = 2,5103 .          N = противления Fal. оказываемого порой, составляет соответственно 1,34 и 66,9 м. При 8 = 8-Ю 6н и прочих равных условиях h < 341 N. Выражение h < 0,014 N верно при Rt = 20-10 6 м, l = 30-IO-6 м, V = 2,2-10-3 м/с, 8 = 2-10-6 м, Дh = 5-10 3 м, а при 8 = 8-10-6 м h < 3,63 N Задавая N, можно определить h.

Большая вариативность переменных в (18) не позволяет перебором параметров наглядно представить результаты возможных вариантов их сочетания. Решить это можно табулированием результатов расчета. Отметим следующее. Каждая трахеида одной своей третью вклинивается радиальными стенками между радиальными стенками двух трахеид следующего уровня, где и расположена основная масса окаймленных пор [7]. При этом на одном погонном метре может быть размещено от 260 до 530 трахеид (в среднем 395). Полагая, что все трахеиды по высоте ксилемы . 2,

Таблица 3

Потери давления на погонном метре трахеидального капилляра ксилемы

N	D 6,	V 3	6,	Интервал изменения Др,МПа при 5-10-6< l < 30-10-6 ми количестве трахеид на 1 м
				260	395	530
1	20	0,28	2	0,073-0,439	0,111-0,667	0,149-0,895
			8	0,000286-0,0018	0,00043-0,0026	0,0006-(0,0035)
		2,2	2	0,572-3,468	0,087-5,27	1,77-7,07
			8	0,0022-(0,0045)	(0,0034)-0,021	(0,0049)-0,029
	40	0,28	2	0,572-3,468	0,87-5,21	1,78-7,07
			8	0,0011-(0,0068)	0,0018-(0,011)	0,0023-(0,0138)
		2,2	2	2,324-13,83	3,53-21,0	4,74-28,19
			8	(0,0091)-0,055	(0,014)-0,083	0,0186-0,111
50	20	0,28	2	0,0014-(0,0088)	0,0022-(0,013)	0,00297-0,018
			8	0,000005-0,0003	0,00008-0,0005	0,00001-0,0007
		2,2	2	(0,0117)-0,069	0,018-0,106	0,024-0,142
			8	0,00004-0,00027	0,00007-0,0004	0,0009-0,0006
	40	0,28	2	(0,0057)-0,035	(0,0087)-0,053	0,0012-0,072
			8	0,000023-0,00014	0,000036-0,0002	0,00005-0,0003
		2,2	2	0,046-0,28	0,071-0,427	0,0948-0,572
			8	0,000182-0,001	0,00028-0,0017	0,00037-0,0022

0,15

(                                                 )                                 .

l

)

черкиванием и скобками. В остальных случаях (шрифт без выделений) величина Др либо значительно превосходит ркор, либо равенство возможно при меньших высотах капилляра.

.                                                   N =                                              l , V

D .

лах 0,073 ^ 28,19 МПа, что значительно превышает р_юр. По мере увеличения 8 (при прочих равных условиях) величина Ар уменьшается: при 8 = 8-10^-6 м ее диапазон — 0,000286 ^ 0,111 МПа. Она увеличивается прямо пропорционально l ,                                                                                                  h .

N                                                                                                 .

Так, при N = 50 и 8 = 2-10^-6 м на одном погонном метре капилляра Ар находится в пределах 0,0014 ^ 0,572 МПа для

Процессы и машины агроинженерных систем

ряда значений l , V , D_т и длины трахеиды Др < р_кор. При 8 = 8·10^–6 м Др < /?кор и находится в пределах 0,000005 ÷ 0,0022 МПа .

Малая величина б характерна для мелких пор с D _ппорядка 810–6 м. В этом случае, учитывая размер торуса, который не может быть меньше d _а, зазор б между ним и стенкой поры не может быть больше 2·10^–6 м. Следовательно, Др велико, и ксилема с таким размером пор не может поднимать воду на большую высоту. Для крупной поры с D п = 30·10^–6 М И d _а = 8·10^–6м величина б может достигать 8- 10^–6 м. При этом Др не велико, и ксилема с такими порами на стенках трахеид может поднимать воду на большую высоту. Этот результат хорошо согласуется с [7], где сказано, что на радиальных стенках, особенно у концов ранних трахеид, имеется от 70 до 90 крупных окаймленных пор с округлыми отверстиями.

Следует заметить, что корневое давление не является постоянной величиной. Оно зависит от условий жизнедеятельности корня и таких факторов, как :

творе и клетках корня минеральных веществ, воды, кислорода и др. Корневое давление может быть значительно ниже 0,15 МПа. Поэтому корневое давление частично или полностью компенсирует Ар, позволяя силам поверхностного натяжения в капиллярах ксилемы поднять воду на максимально возможную высоту. И если корневое давление падает, например, при недостатке влаги в почве, то силам поверхностного натяжения приходится преодолевать силы сопротивления. Они не могут поднять воду на прежнюю высоту, и растение начинает увядать с верхних уровней, где дефицит воды больше.

Выводы.

• 1.    Получено уравнение, позволяющее определить высоту подъема воды в капилляре ксилемы растений с тра-хеидальной проводимостью. При этом учитывается анатомическое строение трахеид и окаймленных пор, а также ориентация последних. Показано, что движение воды через окаймленную пору можно рассматривать как течение воды через капилляр. Его длина равна пути, который проходит вода при обтекании торуса, а диаметр равен величине зазора между поверхностью торуса и внутренней стенкой трахеиды.

• 2.    Определены границы изменения гидравлических потерь при движении воды — как через одиночную окаймленную пору, так и через их совокупность в зависимости от зазора и длины пути, проходимого водой в поре. Показано, что сопротивление одиночной окаймленной поры велико и при скоростях подъема воды в ксилеме 1 – 8 м/час находится в пределах 0,073–28 МПа. При увеличении количества пор на стенке трахеиды гидравлические потери уменьшаются и составляют для тех же скоростей движения воды 0,000005–0,057 МПа.

• 3.    Увеличение диаметра полости трахеиды, диаметра окаймленной поры и торуса (при прочих равных условиях) приводит к росту гидравлических потерь.

• 4.    Увеличение длины трахеиды и зазора между поверхностями торуса и внутренней стенки трахеиды (при прочих равных условиях) приводит к снижению гидравлических потерь. Последнее обусловлено снижением скорости потока в зазоре.

• 5.    При наклонном положении поры на стенке трахеиды необходимо учитывать направленную в сторону подъема воды дополнительную силу, возникающую из-за перераспределения веса воды, действующего на поверхность торуса и стенки поры.

• 6.    Основной силой, осуществляющей подъем воды в ксилеме растений, является сила поверхностного натяжения в менисках капилляров.

• 7.    Полученные результаты позволяют предположить, что при длительном дефиците воды или высоком содержании солей в почвенном растворе корневое давление может быть мало, близко к нулю и даже отрицательно. В этом случае силам поверхностного натяжения приходится преодолевать сопротивление движению воды окаймленными порами. В результате вода в ксилеме не может подниматься на прежнюю высоту, что способствует увяданию, которое начинается с наиболее удаленных от комля концов самых длинных ветвей верхних ярусов растения.