Подход к адаптивной пространственной интерполяции геофизической информации

Одним из источников данных о геофизических процессах являются результаты наблюдений наземных и околоземных информационно-измерительных средств, осуществляющих регистрацию искомых параметров с заданной периодичностью в установленных пространственных точках. Собранная информация помогает исследовать геофизические процессы и понять их природу, а также является важным источником данных для оперативного принятия решений в вопросах, касающихся обеспечения техносферной безопасности [1, 2].

Здесь очевидны две значимые проблемы. Первая из них сопряжена с несовершенством информационно-измерительных средств: приборы выходят из строя или дают кратковременный сбой, тем самым прерывая временной ряд геофизических данных [3]. Вторая проблема характеризуется пространственной неравномерностью расположения измерительных устройств, что не позволяет оценить значения геофизических параметров в тех пространственных обла- стях, где отсутствуют и / или недоступны регистрирующие их приборы [3, 4].

В результате при решении прикладных и научных задач пользователь сталкивается с недостатком пространственных данных. Выраженная пространственная анизотропия геофизических данных не позволяет восстанавливать неполные временные ряды известными статистическими методами, поскольку последние не учитывают особенностей геофизических процессов применительно к различным пространственным областям и условиям.

При этом известные исследования свидетельствуют о статистической однородности пространственных геофизических данных, что выражается в примерно равном изменении значений геофизических параметров в одной пространственной области под воздействием одних и тех же внешних факторов [5, 6].

Примером геофизической информации являются геомагнитные данные, регистрируемые неравномерно распределенными по земной поверхности магнитными обсерваториями и вариационными станциями [7]. Данные используются учеными и исследователями для оценки геомагнитной обстановки при изучении геофизических процессов, а также при решении различных задач [8].

Важно учитывать данную особенность геофизических данных для их интерполяции. Разделенные на пространственные группы данные могут быть определены как статистически однородные и демонстрировать общие вариационные тенденции и характеристики.

1.    Постановка задачи

В общем виде задача пространственной интерполяции может быть представлена следующим образом [9, 10]. Пусть известны атрибутивные значения параметра Z в опорных n пространственных точках ( p 1 ,… p n ), каждая из которых задана парой географических координат ( x i , y i ). Предполагается, что атрибутивный параметр Z является пространственнозависимым. Имеет место множество известных значений параметра Z вида:

{ Z ( P 1 ) ,..., Z ( P n ) } или { Z ( X 1 ,У 1 ) ,..., Z ( X n , У п ) } . (1)

Тогда целью решения задачи пространственной интерполяции является определение значения атрибутивного параметра Z в точке p 0 с координатами ( x 0 , y 0 ) на основе обработки и анализа значений того же параметра в опорных точках ( p 1 ,… p n ). Задача сводится к построению интерполяционной функции:

Z ( p 0 ) ~ Z * ( p 0 ) , (2)

где p 0 – интерполируемая точка с координатами ( x 0 , y 0 ), Z *( p 0 ) – оценка неизвестного значения Z ( p 0 ).

Подавляющее большинство методов пространственной интерполяции построены на соотношении для средневзвешенного пространственного прогнозирования:

n

Z * ( p о ) = ^Z ( Pi ) , (3) i = 1

где p i – опорная точка с координатами ( x i , y i ), Z *( p 0 ) – оценка неизвестного значения Z(p ₀), X i - вес опорной точки p i , n – количество опорных точек.

Значение выражения (3) можно объяснить следующим образом: при прочих равных условиях чем ближе известная точка к искомой, тем большее влияние она оказывает на оценку неизвестного значения Z *( p 0 ). Фактически различие между методами, использующими подобное усреднение, заключается в способе расчета весовых коэффициентов и применения их к опорным точкам.

Произвольная точка p 0 с координатами ( x 0 , y 0 ) должна быть при этом выбрана таким образом, чтобы не совпасть координатно с опорными точками:

P о ( x о , У о ) : ( x о , У о ) * ( х , , y i ) , V i = 1,..., п . (4)

Интерполированная точка может быть переведена в группу опорных. На этой основе могут быть интерполированы новые точки. Однако ошибка восстановления данных при этом тем выше, чем больше в группе опорных точек интерполированных значений.

Необходимо принимать в расчет особенности интерполируемых данных. Так, для обработки геомагнитной информации следует учитывать характер изменения значений параметров поля в зависимости от широтной области: в средних широтах вариации поля минимальны, по мере приближения к полюсам и экватору они становятся более выраженными.

Известные методы пространственной интерполяции демонстрируют отличающиеся по точности результаты на различных пространственных областях при различных внешних факторах и условиях, а также варьирующейся анизотропии значений соответствующего атрибутивного параметра. Если учитывать данное наблюдение, то возможно повысить эффективность применения методов пространственной интерполяции относительно данных, характеризующих некоторый процесс.

2.    Состояние вопроса

Множество методов интерполяции пространственных данных можно разделить на две группы. В основе детерминированных методов лежат функции расстояния между точками [11]. Такие методы характеризуются высокой скоростью обработки и учитывают взаимное расположение объектов. Статистические методы основаны на функции статистического пространственного сходства, которая рассчитывается как глобальная характеристика множества объектов при восприятии их свойств [12]. Их достоинством является чувствительность к разнонаправленности данных, поэтому такие методы чаще используют для интерполяции поверхностей.

Сравнительные характеристики методов пространственной интерполяции представлены в табл. 1. Среди методов указаны и те, что применяются для интерполяции геофизических данных. Анализируя результаты из табл. 1, отметим, что методы наилучшим образом применимы к данным, относительно равномерно распределенным по земной поверхности и характеризующимся минимальной анизотропией атрибутивных значений. Данные, атрибутивные значения которых напрямую зависят от внешних факторов и пространственной области, плохо поддаются восстановлению такими методами.

В контексте современных тенденций активного внедрения искусственного интеллекта и машинного обучения в решение актуальных задач представляется целесообразным отметить известные подходы к пространственной интерполяции, основанные, в частности, на методах глубокого обучения. Так, в работе [13] обсуждаются возможности глубокой нейронной сети Deep Geospatial Interpolation Network (DGIN), которая выявляет пространственные и временные зависимости данных, оценивает соседние значения и выполняет на этой основе интерполяцию. Другой пример – использование для пространственной интерполяции методов геометрического глубокого обучения (Deep Geometric Learning), также ориентированных на отслеживание пространственно-временных зависимостей опорных точек [14] с точки зрения их пространственной симметрии и инвариантности. Перечисленные и другие подобные им методы демонстрируют приемлемое значение среднеквадратической ошибки на тестовых данных. Вместе с тем применение глубокого обучения сопряжено с высокими вычислительными затратами, связанными с обработкой больших массивов данных. Указанные подходы не учитывают влияния внешних факторов и особенности физических процессов, протекающих в соответствующих пространственных регионах. Глубокие нейронные сети не позволяют идентифицировать причины (в частности, физического характера) получения тех или иных результатов интерполяции. Безусловно, как и рассмотренные выше статистические и геостатистические методы, подходы на базе глубокого обучения целесообразно применять на локальных областях – с меньшим числом данных и параметров. Но связанные с этим вычислительные затраты являются неоправданными в контексте получаемого при этом результата (без адаптации подхода).

Необходимо разработать подход, который обеспечит пространственную интерполяцию, учитывающую специфику внешних факторов, в том числе особенности пространственного распределения параметров описываемого процесса. При этом, как показали исследования, рассмотренные методы можно считать эффективными локально: для небольшого набора точек, для относительно регулярной опорной сети точек, для данных, демонстрирующих сравнительно низкую анизотропию внутри некоторого пространственного региона.

Важно использовать преимущества этих методов и реализовать их комбинирование в зависимости от расположения опорных пространственных точек, внешних факторов, а также особенности описываемых обрабатываемыми данными процессов.

Табл. 1. Сравнительные характеристики методов пространственной интерполяции

Название метода	Тип метода	Положение опорных точек	Внешние факторы	Значимые недостатки
Метод линейной интерполяции [15]	Статистический	Нет	Нет	- увеличение значения ошибки интерполяции по мере удаления опорных точек друг от друга
Метод обратных взвешенных расстояний (Шепарда) [16]	Детерминированный	Да	Нет	-    эффективен только на регулярной пространственной сетке -    увеличение значения ошибки интерполяции по мере удаления опорных точек друг от друга
Метод полиномиальной регрессии [17]	Статистический	Нет	Нет	-    не учитывает пространственную привязку опорных точек -    применим только для данных с минимальной пространственной анизотропией
Метод нерегулярной триангуляционной сети [18]	Статистический	Нет	Нет	-    чрезмерная сложность создания уровней детализации и низкая реактивность при реализации -    увеличение значения ошибки интерполяции по мере удаления опорных точек друг от друга
Метод кригинга [19, 20]	Детерминированный	Да	Нет	-    эффективен при большом количестве опорных точек на интерполируемой поверхности -    увеличение значения ошибки интерполяции по мере удаления опорных точек друг от друга
Радиальная интерполяция [21]	Детерминированный	Да	Нет	- применим только для данных с минимальной пространственной анизотропией
Метод градиентных плоскостей [22]	Детерминированный	Да	Нет	-    эффективен только на регулярной пространственной сетке -    увеличение значения ошибки интерполяции по мере удаления опорных точек друг от друга -    применим только для данных с минимальной пространственной анизотропией
Метод сплайнов [23]	Детерминированный	Да	Нет
Метод трендов [24]	Детерминированный	Да	Нет

3.    Характеристика исходных данных

В качестве исходных данных рассматриваются результаты наблюдения параметров геомагнитного поля магнитными обсерваториями и вариационными станциями. При этом особенности распределения данных таковы, что для определенных пространственных групп наблюдается тенденция повторяемости значений [3, 4].

Нередкими являются ситуации, при которых необходимо оценить геомагнитную обстановку в тех пространственных регионах, где отсутствуют сред- ства регистрации параметров геомагнитного поля [3]. Такие задачи часто связаны с обеспечением техно-сферной безопасности. Так, известны эффекты воздействия геомагнитных вариаций на точность бурения скважин при использовании буров с магнитной системой ориентации, а также насыщение стали сердечников ввиду генерации квазистационарных геоин-дуцированных токов при проявления разности потенциалов в удаленных точках на земной поверхности в нулевой последовательности линий через заземленные нейтрали трансформаторов [3].

Специфика геомагнитных данных определяется динамикой их изменения по мере движения по географическим широтам и долготам. Так, в области средних широт значения параметров геомагнитного поля зависят от наименьшего количества внешних факторов [4]. При этом по мере приближения к экватору и полюсам число факторов, влияющих на результаты наблюдений, возрастает, что приводит к росту неопределенности данных о состоянии геомагнитного поля, но повышает информативность каждой итерации геомагнитного мониторинга.

Кроме того, было установлено, что на значения параметров геомагнитного поля и его вариаций в пределах одного широтного диапазона оказывают влияние одни и те же внешние факторы, в результате чего информационная энтропия с изменением географической долготы остается относительно неизменной. В общем виде это свидетельствует о высокой связности процессов, определяющих регистрируемые значения на различных географических долготах и одном диапазоне широт.

4.    Описание предлагаемого подхода к интерполяции

Особенности геопространственных данных, связанные с выраженной зависимостью вариабельности и созависимости значений от пространственного расположения опорных точек, представляется целесообразным использовать для повышения эффективности пространственной интерполяции. Предлагается в зависимости от полученных на этапе предварительной обработки данных результатов для отдельных пространственных областей и / или при определенной совокупности внешних факторов использовать те методы интерполяции, которые демонстрируют наилучшие результаты с точки зрения минимизации ошибки восстановления данных.

В этой связи процедуру пространственной интерполяции необходимо предварить дополнительными действиями, направленными на оценку эффективности методов интерполяции в различных пространственных областях и / или при различных внешних факторах, которые могут оказывать влияние на результат интерполяции. Для этого должна быть проведена серия вычислительных экспериментов на различных регионах и при различных условиях (при необходимости), обеспечивающая сравнительный анализ известных методов пространственной интерполяции в контексте значения обеспечивающей их ошибки восстановления данных.

При этом пространственная зависимость атрибутивных значений позволяет предположить, что при отборе в вычислительный эксперимент соответствующие методы интерполяции должны учитывать пространственное распределение опорных точек. Для повышения наглядности экспериментов необходимо заранее выделить исследуемые методы интерполяции и объединить их в табличный реестр, в котором должны фиксироваться результаты оценки эффективности каждого метода.

В контексте обработки геомагнитной информации, источниками которой являются пространственно неравномерно распределенные обсерватории, анализ эффективности методов интерполяции был проведен применительно к перечисленным в табл. 1. Все пространственные регионы были разделены на группы: высоко-, низкоширотные и приэкваториальные. Физически классификация обусловлена спецификой вариаций поля: от слабой динамики в средних широтах к выраженной по мере приближения к экстремальным широтам.

Анализ эффективности методов пространственной интерполяции был проведен для каждого из регионов по имеющимся годовым геомагнитным данным, регистрируемым магнитными обсерваториями и станциями с шагом в 1 мин. Для простоты была рассмотрена горизонтальная составляющая вектора геомагнитного поля.

Для проведения вычислительных экспериментов из исходных данных на каждом этапе изымалась одна пространственная точка, атрибутивное значение в которой было рассмотрено как неизвестное и требующее вычисления методами интерполяции. Далее результат сравнивался с оригинальным значением. Для каждой комбинации факторов было проведено порядка 50 вычислительных экспериментов, что позволило оценить качество методов пространственной интерполяции.

В качестве дополнительных параметров были рассмотрены значения Kp-индексов, характеризующие геомагнитную обстановку в трехчасовые временные интервалы. По аналогии с пространственной классификацией были выделены три варианта геомагнитной обстановки, при которых были исследованы перечисленные в табл. 1 методы. Так, эксперименты были проведены в условиях спокойной магнитосферы, слабой и сильной магнитной бури, что позволило оценить разницу в результатах пространственной интерполяции не только в контексте выделенной пространственной области, но также и при заданных условиях. Такой подход может быть расширен введением дополнительной декомпозиции пространственных областей, а также внешними факторами, которые могут повлиять на результаты интерполяции.

На последующем этапе для выделенных пространственных областей и значений параметров внешних факторов была проведена пространственная интерполяция методами, перечисленными в табл. 1. Методы показали хорошие результаты пространственной интерполяции в средних широтах в условиях спокойной магнитосферы. При этом по мере приближения к экстремальным широтам качество применяемых методов существенно разнится. Значимый вклад в формируемый результат обработки вносят и указанные внешние факторы: чем выше значения индексов геомагнитной активности, тем больше ошибка пространственной интерполяции.

По результатам вычислительных экспериментов на высокоширотных геомагнитных данных было установлено, что наименьшая ошибка восстановления при любой геомагнитной обстановке обеспечивается методами кригинга [19, 20] (табл. 2). Указанные методы базируются на пространственной модели опорных точек, представляемой в виде вариограммы. Соответствующая модель используется для прогнозирования атрибутивных значений в искомых пространственных точках.

Метод кригинга основан на том принципе, что опорные точки имеют тем больший вес в прогностической модели, чем ближе они пространственно расположены к искомой точке. При этом особенностью метода, благодаря которой обеспечивается приемлемая точность восстановления, является то, что он опирается на модель некоторой пространственной структуры, формируемой с помощью свойств второго порядка – вариограммы или ковариации по случайной функции Z ( x ) [20].

Метод кригинга использует средневзвешенное значение наблюдений z ( x i , y i ) в качестве оценки. При этом оптимальные веса опорных точек в линейной прогностической модели означают, что окончательная оценка должна быть несмещенной и иметь минимальную дисперсию ошибки среди всех несмещенных линейных предикторов. Эти результирующие веса будут зависеть от предположений о среднем значении m ( z ), а также от вариограммы или ковариационной функции Z ( x ).

Применение кригинга для вычисления значения Z ^*( x 0 , y 0 ) в точке ( x 0 , y 0 ) на основе n точек вида Z ( x i , y i ) сводится к линейно регрессионной оценке вида:

Z * ( x 0 , y 0 ) - m ( x 0 , y 0 ) =

= E n^‘ I Z ( x,y i ) - m ( X i ,y i ) ] ,

где m ( x i , y i ) и m ( x 0 , y 0 ) – математическое ожидание Z ( x i , y i ) и Z ( x 0 , y 0 ).

При этом основная сложность в определении веса X I так, чтобы минимизировать дисперсию [19]

о E ( X i ,y i ) = Var { Z * ( x 0 , y 0 ) — Z ( X i ,y i ) } .             (6)

Случайная функция Z ( x i , y i ) имеет вид:

Z ( X, y i ) = m ( X i , y i ) + R ( X i , y i ) ,                       (7)

где m ( x i , y i ) – детерминистический тренд, R ( x i , y i ) – стационарная случайная функция с математическим ожиданием, равным нулю, и ковариацией C R ( h )%

Cov { R ( X i , y i ) , R ( X i , y i + h ) } =

= E { R ( x , -, y^ R ( X i ,y i + h ) } = C R ( h ) .

Таким образом, математическое ожидание пространственно-зависимого атрибутивного значения Z ( x i , y i ) в точке ( x i , y i ) будет эквивалентно значению тренда [20]:

E { Z ( X, y i ) } = m ( X i , y i ) . (9)

В условиях спокойной магнитосферы наиболее эффективна пространственная интерполяция посредством простого кригинга, когда среднее значение m ( z ) постоянно и известно на всей области исследования. Тогда оценка простого кригинга имеет вид:

Z * ( X 0 , y 0 ) = m + E n =M Z ( X i , y i ) - m ]• (10)

В простом кригинге весовые коэффициенты определяются только корреляцией, которая строится на основе исходных данных. Если имеется несколько наборов данных, описываемых одинаковыми функциями ковариации в одних и тех же точках, то для моделирования в произвольной точке достаточно решить систему уравнения кригинга один раз, чтобы найти веса, которые затем могут использоваться для всех остальных точек. Основным недостатком при этом можно обозначить предположение, что среднее значение постоянно, в то время как в большинстве случаев такое невозможно.

В условиях неспокойной магнитосферы наилучшие результаты показал обычный кригинг [19]. Данный метод основан на предположении, что среднее значение m ( z ) постоянно, но неизвестно на всей области исследования, т.е. для всех точек ( x i , y i ) при i = 1,.. n m ( z ) = const.

Оценка обычного кригинга может быть представлена как линейная комбинация исходных данных вида:

Z * ( x 0 , y 0 ) = E ^Z ( X i , y i ) • (11)

Простой кригинг удобен для локальной оценки, поскольку его применение не требует, чтобы среднее было постоянным на всей области, оно постоянно только в непосредственной близости к точке, для которой выполняется интерполяция, то есть в ее окрестности.

В области сильной магнитной бури наилучшие показатели по минимизации ошибки пространственной интерполяции в ходе проведенных вычисли- тельных экспериментов показал метод универсального кригинга с константной функцией (кригинг с трендом) [20]. В этом случае моделируется тренд данных как линейная комбинация базисных функций fk (x 0, y 0) с коэффициентами Pit. Последние неизвестны и постоянны внутри окрестности оцениваемой точки (x0, y0):

Z * ( x 0 , y 0 ) = ^ n f ( X i , y , -) p k + R ( x 0 , y 0 ) . (12)

Анализ результатов экспериментов показал, что вариации кригинга используют статистические модели для более точного моделирования пространственных данных по сравнению с иными методами при тех же условиях. Кригинг позволяет оценивать точность результатов пространственной интерполяции исходя из соответствующих статистических моделей. В условиях высокой неопределенности для обозначенных областей и внешних факторов это свойство представляет особую значимость.

Далее анализ результатов проведенных вычислительных экспериментов показал, что в низких и средних широтах наилучшие результаты пространственной интерполяции демонстрирует триангуляция Делоне, описание которой представлено выше [18]. С точки зрения алгоритма, реализация метода триангуляции Делоне может быть выполнена следующим образом.

Табл. 2. Результаты оценки значения метрики RMSE методов интерполяции применительно к геомагнитным данным

3 В CO О Oh EC H О О s о u Он W к	Oh о о о U to U о	Методы интерполяции, значение среднеквадратической ошибки RMSE
		s s	Ph О	EC о § S 2 § & c £	E E S 4 Ph W H EC	E S S §	4 Ph E a 4 о 2	ffl E E S	X e н о S * °    o я 2 2 & S	О Ч О 2	ffl ч о
Область высоких широт	0,…,4	3,23	5,56	2,98	1,82	1,6	5,56	3,18	4,14	5,12	4,98
	5,…,4	4,16	6,12	3,12	2,19	1,89	6,12	4,78	6,29	7,15	6,89
	7,…,9	5,32	8,45	7,15	3,45	2,51	8,45	6,97	7,15	9,12	8,97
Область средних широт	0,…,4	1,2	1,51	1,78	0,17	0,54	1,51	3,21	4,78	5,97	5,3
	5,…,4	2,5	4,8	2,41	0,65	0,97	4,8	4,86	5,9	5,95	6,3
	7,…,9	3,1	5,73	5,53	1,31	1,35	5,73	12,1	10,4	11,5	11,9
Область низких широт	0,…,4	18,6	17,12	10,15	0,22	7,36	17,12	10,6	11,8	12,1	11,78
	5,…,4	22,19	20,45	15,92	2,12	10,12	20,45	15,8	16,2	16,98	16,45
	7,…,9	40,1	28,34	27,6	3,5	12,7	28,34	28,7	28,9	27,6	25,1

На первом этапе осуществляется сортировка имеющихся вершин с координатами ( x i , y i ) так, чтобы выделить супертреугольник. Создается перечень треугольников, подлежащих удалению, а также список вершин.

Далее перебираются вершины и треугольники из сформированных ранее списков. Для каждого треугольника предпринимается попытка создать описанную вокруг него окружность. Если окружность охватывает вершину, то треугольник переносится в список запрещенных. Если окружность построить невозможно из-за непересекающихся перпендикулярных биссектрис, то треугольник перемещается в список для удаления. После перебора всех вершин и треугольников все треугольники, попавшие в список на удаление, удаляются.

Формируется список запрещенных ребер, для чего перебираются запрещенные треугольники и для каждого из них последовательно перебираются его ребра. Уникальные ребра добавляются в список ребер, а все запрещенные треугольники удаляются из списка.

Ребра из списка снова перебираются. Для каждого уникального ребра и текущей вершины создается новый треугольник, который добавляется в список треугольников. Далее удаляют все те треугольники, кото- рые делят свои вершины с вершинами супертреугольников. Результатом является перечень сформированных треугольников, которые используются для вычисления недостающих значений при интерполяции.

Таким образом, результаты экспериментов свидетельствуют о том, что различные методы пространственной интерполяции демонстрируют неодинаковую эффективность для различных областей и внешних факторов. В этой связи целесообразным представляется динамический подбор методов интерполяции по результатам заранее проведенных вычислительных экспериментов.

5.    Алгоритм и технологии реализации решения

На начальном этапе алгоритм предполагает выполнение вычислительных экспериментов для набора данных с целью выявления результативности методов для областей и факторов.

Далее модели пространственной интерполяции должны быть обучены на имеющихся наборах пространственных данных. Пул методов должен быть полностью подготовлен для применения, в том числе в динамическом режиме для восстановления значений в точках. Выполняется непосредственно процедура точечной интерполяции. Для каждой простран- ственной точки оценивается ее принадлежность пространственному региону, выделенному и проанализированному ранее. В зависимости от геопространственной привязки выделяется группа методов интерполяции с наилучшими показателями эффективности восстановления данных.

Здесь же оцениваются значения внешних факторов. В совокупности с параметрами выделенного пространственного региона, к которому относится восстанавливаемая точка, значение такого фактора определяет, какой метод следует применить для обработки опорных точек.

Так, в случае интерполяции геомагнитных данных определяющими являются принадлежность точки пространственному региону, с одной стороны, и параметры геомагнитной обстановки по значению Kp-индекса, с другой. Из пула методов выбирается кригинг или триангуляция Делоне с выполненной настройкой. Выбранный метод используется для вычисления искомого атрибутивного значения в заданной пространственной точке.

Для пользователя, решающего задачу вычисления атрибутивного значения в произвольной точке, алгоритм может быть представлен следующей последовательностью этапов. Пользователь задает искомые временные параметры, либо могут быть использованы значения, заданные по умолчанию (например, текущие).

Далее необходимо определить значения внешних факторов, способных оказывать влияние на результат восстановления данных. Так, в случае геомагнитных данных это значения Kp-индекса геомагнитной активности.

Пользователь определяет пространственные точки для выполнения процедуры интерполяции. На серверной стороне обрабатываются параметры пространственной области и значения внешних факторов, на основании чего выделяется наиболее эффективный метод интерполяции. Серверный сценарий, реализующий метод интерполяции, запускается на выполнение с набором входных параметров с клиентской стороны, в результате чего формируются атрибутивные значения, откликом направляемые пользователю для последующей работы.

Для обеспечения доступа к возможностям решения широкому кругу пользователей и приложений представляется целесообразным его веб-ориентированная реализация. Вычислительно затратные процедуры, связанные как с обработкой геопространственных данных, так и подбором методов интерполяции с их последующим применением, реализуются на серверной стороне в распределенной архитектуре веб-приложения на языке программирования Python на базе архитектуры MVC (Model – View – Controller) [21, 26], которая разделяет приложение на три компонента: модель, представление и контроллер.

Целесообразно использовать программное решение и так, что в качестве клиента выступает некоторое стороннее приложение, использующее запрашиваемые пространственные и атрибутивные данные для обработки, анализа и / или визуализации. Тогда представление может быть построено на базе микросервисного паттерна проектирования по типу API [27].

6.    Апробация и оценка качества решения

Для апробации решения был разработан исследовательский прототип веб-приложения, обеспечивающего пространственную интерполяцию с учетом эффективности доступных методов при различных сочетаниях внешних и внутренних факторов. Для повышения наглядности результаты интерполяции обработаны и визуализированы на клиентской стороне в виде интегрированного пространственного слоя на виртуальном глобусе (рис. 1).

В качестве инфраструктуры исследовательского прототипа была реализована вариация MVC-паттерна, построенная на базе серверного фреймворка Django. Серверные сценарии реализованы на языке программирования Python [3 –4, 25], клиентская составляющая основана на языке программирования JavaScript. Кроме того, на клиентской стороне обработка, анализ и визуализация пространственных данных реализована на базе ArcGIS API for JavaScript.

В качестве исходных данных выступают результаты наблюдений параметров геомагнитного поля, полученные магнитными обсерваториями в рамках проекта SuperMAG . Входная информация представлена в виде данных, прошедших обработку и интегрированных в GeoJSON-файл. Данные были отобраны таким образом, чтобы по ним можно было оценить широкий спектр временных (суточные, сезонные, годовые) и возмущенных (связанных с повышенной геомагнитной активностью) вариаций геомагнитного поля. В годовых наблюдениях представлены данные, отражающие указанные вариации, поэтому их применение представляется в целом достаточным для оценки эффективности предложенного решения.

Серверные сценарии, реализующие подборы наиболее эффективных в заданных условиях методов пространственной интерполяции, функционируют в фоновом режиме. Пул исходных методов представлен перечнем, приведенным в табл. 1. Каждому методу поставлена в соответствие реализующая его в серверном сценарии программная функция, вызываемая с помощью MVC-контроллера при запуске фонового процесса.

В качестве внешнего параметра выступает магнитная обстановка, которая определяется значением Kp-индекса геомагнитной активности. Вместе с искомой точкой, для которой необходимо вычислить атрибутивное значение, на вход серверным сценариям подается временная метка. На основании этого определяется значение Kp-индекса, также влияющее на выбор метода интерполяции.

Последующая обработка выполняется на серверной стороне и заключается в вычислении атрибутивного значения заданной пространственной точки с указан- ными географической привязкой и временной меткой. В соответствии с проведенными исследованиями при этом задействованы методы кригинга для высокоширотных и триангуляции Делоне для низкоширотных точек, что реализуется серверными программными сценариями.

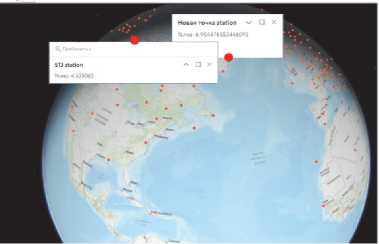
Рис. 1. Экранные формы, демонстрирующие результаты интерполяции геомагнитных данных в высокоширотной области методом кригинга (а) и низкоширотной области методом триангуляции Делоне (б)

Табл. 3. Результаты оценки значения метрики R2 методов интерполяции применительно к геомагнитным данным

OJ и и о та 2 & я о 2 о s к &	Он « ^ ей И та н и s м та й та о U О	Методы интерполяции, коэффициент детерминации R2
		S о	о	2 « § Рн	та О S Ч Н Ч	S S	та Он н ч о си	W а й сч К ч S CU ч н та И Он Я	X 2 эк я н о s й	и	и о 3	я © е s
Область высоких широт	0,…,4	0,32	-0,82	0,21	0,38	0,47	-0,82	0,18	0,04	-0,76	0,18	0,47
	5,…,4	0,36	0,15	0,44	0,58	0,75	0,15	0,33	0,18	-0,13	0,09	0,75
	7,…,9	-0,21	0,14	0,18	0,33	0,81	0,14	0,37	0,15	-0,17	-0,98	0,81
Область средних широт	0,…,4	0,63	0,47	0,35	0,88	0,54	0,47	0,23	0,17	-0,91	-0,8	0,88
	5,…,4	0,35	0,15	2,41	0,76	0,56	0,15	0,02	-0,79	-0,65	-0,6	0,76
	7,…,9	0,22	-0,23	-0,93	0,52	0,44	-0,73	-0,21	-0.4	-0,7	-0,12	0,52
Область низких широт	0,…,4	-0.87	-0,78	-0,25	0,84	-0,46	-0,78	-0,56	-0,48	-0.71	-0,67	0,84
	5,…,4	-0.98	-0.93	-0,52	0,62	-0,32	-0.93	-0,58	-0.72	-0.85	-0,65	0,62
	7,…,9	-0,9	-0,81	-0,75	0,42	-0,41	-0,81	-0,82	-0,78	-0,71	-0,83	0,42

Экспериментальные исследования проводились на геомагнитных данных в различные периоды геомагнитной активности на клиентской стороне с применением ЭВМ (СPU Intel Core i5 10300H, 2,5– 4,5 ГГц, оперативная память 4 ГБ, скорость интер-нет-соединения ~52.4 Мбит/с) и на серверной стороне (на базе веб-сервера с процессором 72 * Intel(R) Xeon(R) Gold 6140 CPU, 2.30 ГГц). При оценке времени отклика от сервера установлено, что выполнение запроса занимает ~12 с, что соответствует требованиям к производительным вебприложениям. Оценка ошибки интерполяции в сравнении с известными подходами показала ее сокращение в среднеширотных областях – на 4,71 нТл, в высокоширотных областях – на 4,95 нТл, в низкоширотных областях – на 16,7 нТл. Сопоставимые результаты показал анализ значения коэффициента детерминации (табл. 3).

Заключение

Одной из проблем при работе с пространственной информацией является ее выраженная пространственная анизотропия. Источники информации неравномер- но распределены по земной поверхности, что создает сложности при изучении различных процессов и явлений, а также в процессе принятия решений.

Примером такой информации являются геомагнитные данные. Их неравномерное распределение по земной поверхности создает сложности в использовании данных как при изучении геомагнитного поля, так при принятии решений на этой основе. Известные методы интерполяции здесь показывают себя недостаточно эффективно: не учитывают их пространственной привязки, а также не принимают в расчет зависимость данных от внешних факторов и их неоднородность для различных областей.

Предлагается подход, основанный на комбинировании методов интерполяции, демонстрирующих наилучшие результаты восстановления данных при различных сочетаниях внешних и внутренних условий. Предлагается предварительно оценивать значение ошибки интерполяции, которую обеспечивают методы восстановления для различных пространственных областей и внешних факторов. Далее определяется принадлежность восстанавливаемого значения области, оцениваются значения факторов и опре- деляется наиболее эффективный метод, который и применяется для восстановления.

Результаты экспериментов показали, что применение предложенного подхода позволяет снизить значение ошибки восстановления геомагнитных данных по сравнению с известными подходами в среднеширотных областях – на 4,71 нТл, в высокоширотных областях – на 4,95 нТл, в низкоширотных областях – на 16,7 нТл. В контексте дальнейших исследований планируется дополнить пул методов локальной интерполяции подходами на основе методов глубокого обучения для повышения лучших метрик восстановления данных.

Исследование выполнено при поддержке Российского научного фонда (проект No 21-77-30010).

Авторы благодарят рецензентов за ряд конструктивных замечаний и предложений, позволивших существенно улучшить работу.