Подход к формализации индивидуального маршрутного проектирования

поверхностей может быть обеспечено выполнением относительно несложных методов формообразования. Качество изделия в целом определяется геометрической точностью, микрогеометрическими и физико-механическими характеристиками отдельных обработанных поверхностей и точностью взаимного расположения поверхностей. Такие показатели качества обеспечиваются, соответственно, выбором не только методов окончательной обработки, но и выбором базовых поверхностей и последовательности обработки и смены баз. Качество и точность обработанной поверхности оценивается комплексом показателей, каждый из которых можно рассматривать как параметр технологического метода, с помощью которого получено определенное состояние поверхности изделия. Совокупность диапазонов значений технологических показателей для различных методов обработки называют таблицами точности обработки и используют в качестве информационной базы технологического проектирования. Основным недостатком традиционных таблиц точности, фактически определяющим невозможность формализованного решения задачи проектирования последовательности обработки, является отсутствие значений, определяющих величины изменения технологических показателей при каждом последующем переходе обработки. Кроме того, сами значения технологических показателей, приводимые в справочной литературе [ 9 9], также являются неоднозначными. Как следствие, достоверность результатов неформализованного проектирования последовательности обработки на базе нечетких исходных данных требует проверки в условиях опытного производства.

Если каждый из технологических показателей метода обработки рассматривать как случайную величину [5], то подход к проектированию последовательности обработки может быть следующим – последовательность обработки формируется таким образом [1,7], чтобы каждая последующая технологическая операция существенно улучшала показатели качества и точности изделия. Предположим, что 2 метода обработки, смежные в технологической последовательности, существенно различаются по достижимым значениям показателя, если случайные величины, определяющие эти методы, принадлежат различным генеральным совокупностям. Традиционные [2,3] статистические критерии – Стьюдента, Крамера-Уэлча и др. – не позволяют оценить сходство или различие случайных величин с заранее неизвестным законом распределения на основании анализа выборочных совокупностей бесконечно большого объема. Такие случайные величины составляют содержание таблиц точности обработки. Решить задачу сравнения двух случайных величин можно предположив, что законы распределения вероятностей для определенных производственных условий являются одинаковыми и используя в качестве критерия коэффициент вариации (1) – величину [1010] отношения стандартного отклонения S к среднему значению Xmid, не зависящую от объемов выборочных совокупностей. В соответствии с теоремой о сложении случайных величин X1 и X2 с одинаковыми законами распределения, коэффициент вариации разности случайных величин без учета знака можно определить:

v =  S 212 + Si

mid mid

X 1   - X 2

Закон распределения случайной величины Δ X =| X 1 ^mid – X 2 ^mid | совпадает с законами распределения сравниваемых случайных величин. Легко заметить, что величина

A Z =

mid mid

1 X 2

S ls b S s?

обратная по отношению к вариации разности (1) представляет собой стандартизованное и нормализованное значение случайной величины Δ X , которое можно использовать для оценки вероятности нахождения произвольного значения случайной величины в заданном интервале. Таким образом, коэффициент вариации разности (1) можно использовать, так же как и разность Δ Z (2), в качестве статистического критерия, определяющего сходство двух случайных величин.

Анализ (рис. 1) наиболее часто используемых в технологическом проектировании законов распределения вероятностей позволяет сделать следующее заключение – доверительная вероятность, рассчитанная для общепринятых [1010] пороговых значений коэффициента ва- риации (V≤0,17 или V≤0,33) в случае распределения Симпсона и равновероятного распределения безусловно выше, чем для нормального распределения, следовательно условие сходства значений разности случайных величин тем более выполняется и выводы, сделанные для закона нормального распределения также справедливы.

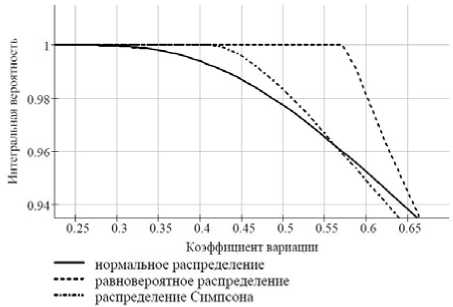
Рис. 1. Зависимость интегральной вероятности от вида распределения

Проведем оценку существенности различий технологических параметров для отдельных этапов механической обработки. Статистический анализ справочной и научно-технической литературы позволил определить технологические параметры основных этапов механической обработки (табл. 1). Для каждой пары методов обработки (табл. 1) рассчитаны величины изменения технологических показателей. Оценка вероятности в соответствии с коэффициентом вариации (1) показывает достаточную достоверность результатов расчета (табл. 2) – в среднем 97%.

Таблица 1. Интервалы значений технологических параметров этапов обработки

Этап обработки		Квалитет точности IT		Шероховатость поверхности R a , мкм
0	заготовка	14	17	18,75	80,00
1	черновая	13	16	8,00	39,17
2	получистовая	12	13	5,90	11,75
3	чистовая	9	11	2,10	4,35
4	тонкая	7	8	0,27	1,73
5	отделочная	5	7	0,10	0,61
6	доводочная	5	7	0,02	0,16

Значения в табл. 2 сгруппированы следующим образом: выше главной диагонали в каждой части таблицы приведена величина изменения технологического показателя в результате осуществления «следующего» этапа обработки после «предыдущего». Ниже главной диагонали – оценка достоверности изменения. Оцен- ка достоверности симметрична величине изменения относительно главной диагонали матрицы. Например, выполнение отделочной обработки после тонкой позволяет повысить точность вы- полняемых размеров на 1-2 квалитета точности с достоверностью более 99,9% и уменьшить высоту микронеровностей Ra в среднем в 2,8 раза с вероятностью 98,8%.

Таблица 1. Повышение точности и качества обработки

Предыдущий этап обработки		Повышение точности (разность)							Повышение качества (отношение)
		Следующий этап обработки							Следующий этап обработки
		0	1	2	3	4	5	6	0	1	2	3	4	5	6
0	Заготовка		1,0	3,0	5,5	8,0	9,5	9,5		2,1	5,6	15,3	49,2	139,4	548,6
1	Черновая	0,843		2,0	4,5	7,0	8,5	8,5	0,976		2,7	7,3	23,5	66,6	262,0
2	Получистовая	1,0	1,0		2,5	5,0	6,5	6,5	1,0	0,995		2,7	8,8	24,9	98,1
3	Чистовая	1,0	1,0	1,0		2,5	4,0	4,0	1,0	1,0	1,0		3,2	9,1	35,8
4	Тонкая	1,0	1,0	1,0	1,0		1,5	1,5	1,0	1,0	1,0	1,0		2,8	11,1
5	Отделочная	1,0	1,0	1,0	1,0	1,0		0,0	1,0	1,0	1,0	1,0	0,988		3,9
6	Доводочная	1,0	1,0	1,0	1,0	1,0	0,000		1,0	1,0	1,0	1,0	1,0	0,998

Примечание: жирным шрифтом выделены значения, приблизительно соответствующие общепринятым представлениям о структуре технологического процесса

Дополнение традиционных (табл. 1) таблиц точности обработки достоверными данными о величинах изменения технологических показателей позволяет применить к проектированию последовательности обработки не только теоретико-множественные алгоритмы [66], но и методы дискретной математики. Предлагаемая методика статистического анализа нормативносправочных массивов лежит в основе разрабатываемой в ВолгГТУ информационной системы для автоматизированного проектирования и оптимизации последовательности обработки поверхностей. Разрабатываемый программноинформационный комплекс представляет со- бой самостоятельный функциональный модуль системы более высокого уровня. На рис. 2 приведен пример вызова расчетного модуля из пакета программ AutoCAD. Исходные данные для построения последовательности обработки могут быть введены с помощью диалоговых окон программы, либо «прочитаны» непосредственно с электронного чертежа изделия. Результатом расчета является последовательность обработки (рис. 4), обеспечивающая получение заданного качества поверхности и оценка вероятности получения требуемого качества. Результат расчета представляется в виде графа вариантов (рис. 3) и текста (рис. 4).

СапрТП

Окно Справка

Оптимизация маршрута обработки поверхности

Информационно-справочная система обработки

Рис. 2 . Вызов модуля проектирования последовательности обработки

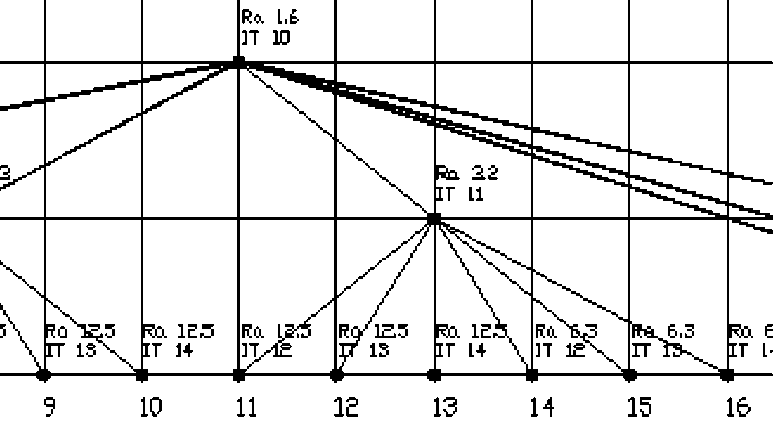
Рис. 3. Фрагмент дерева вариантов обработки зя деталь ^ 12 мм, Ra 1,6 квалитет 10

>н при продольной подаче черновое  12  £5 )   < Точение при продо/ьноп подаче! получисговое  И  6,3 )   < Точение при пр при продольной подаче' черновое  13  25 >   < Точение при продольной подаче, палучиотрпсе  11  6,3 >   \ Точение при пг при продольной подаче! черновое  14  25 )   ( Точение при продольной подаче' получиставое  И  6,3 )   < Точение при пг при продольной подаче' черновое  12  L2.5 )   ( Тачение при продольной подаче' полутоновое  11  63 )   ( Точение приг при продольной подаче' черновое  13  12.5 )   ( Точение при продольной подаче, полутоновое  И  63 )   ( Точение приг при продольной подаче' черновое  14  12,5 >   < Точение при продольной подаче получиотовое  11  6,3 >   < Точение приг при продольной подаче! черновое  13  25 )   ( Точение при продольной подаче! поличиотовое  12  6.3 )   ( Точение прип при продольной подаче' черновое  14  25 )   ( Точение при продольной подаче' по/нчиотовое  12  6,3 )   < Точение прип

Рис.4. Фрагмент списка вариантов последовательности обработки

Вывод: предлагаемый подход позволяет достоверно определять величины повышения точности и качества, которые можно рассматривать в качестве критериев формализованного проектирования технологических процессов. Проверка достоверности получаемых результатов может быть выполнена с использованием методики размерного анализа технологических процессов.