Подход к формированию значения метрики сетевого маршрута

В информационно-вычислительных сетях, как глобальных, так и локальных, каждый сетевой маршрут включает в себя такие параметры, как адрес субъекта, к которому осуществляется доступ (адресат), перечень сетевых узлов (маршрутизаторов) и метрику маршрута [5].

Параметр «метрика» становится актуальным в случае, когда адресат оказывается достижим для отправителя (субъекта сети, осуществляющего доступ) более чем одним путем, то есть набором альтернативных маршрутов. В этом случае метрика как показатель уровня предпочтения в какой-либо одинаковой для всех маршрутов ценовой шкале становится определяющей для выбора конкретного маршрута.

Задача назначения метрики каждому из альтернативных маршрутов в случае применения принципа маршрутизации от отправителя представляется актуальной.

Постановка задачи

В качестве ценовой шкалы могут быть использованы: количество узлов сети (маршрутизаторов), которые должно пройти сообщение от отправителя к адресату; временная задержка, обеспечивающая преодоление того или иного маршрута; надежность маршрута, выраженная через относительное количество ошибок при прохождении сообщением

Баглюк Сергей Иванович кандидат технических наук, доцент, преподаватель 24-й кафедры. Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: интеллект homo sapiens. Автор более 20 опубликованных научных работ.

маршрута; вектор расстояния при дистанционно-векторной маршрутизации, который определяется как сумма фрагментов (стоимостей) всего пути.

Принцип маршрутизации от отправителя (маршрутизация от источника) применяется как при классическом многошаговом алгоритме маршрутизации в версии 4-го протокола IP (IPv4), так и в качестве одного из основных в версии 6-го протокола IP (IPv6). Суть принципа заключается в том [2], что отправитель задает в отправляемом в сеть пакете полный маршрут его следования через все промежуточные маршрутизаторы. Тем самым отправитель каждому маршруту ставит в соответствие показатель уровня предпочтения – метрику. Чем меньше значение метрики, тем предпочтительнее маршрут. Ситуацию с равными значениями метрик (балансировку) (ECMP) опустим.

Рассмотрим вариант назначения метрики отправителем на основе статистических данных о количестве потерянных пакетов из серии тестовых пакетов при их прохождении по каждому из альтернативных маршрутов в течение определенного временного интервала, например суток. Суточный временной интервал интересен тем, что он характерен цикличностью загрузки каналов: спонтанно-пиковыми загрузками в дневное время и относительно стабильным уровнем загрузки в ночное время (выполнение бэкапов, плановых репликаций баз данных и др.).

Для этого введем понятие граничного значения временной задержки прохождения пакета как времени ожидания, мс, ответа на тестовый пакет, соответствующего заданному сообщению запроса Если ответное сообщение не получено в течение времени ожидания, отображается сообщение об ошибке, и тестовый пакет считается потерянным (сообщение «превышен интервал ожидания для запроса»).

Наиболее простой способ получения статистики о потерянных пакетах из каждой одинаковой тестовой серии при их прохождении по альтернативным маршрутам – воспользоваться командой ping (в терминале ОС семейства Linux или командной строке ОС семейства Windows) с ключами, позволяющими задавать количество тестовых пакетов в серии (количество пакетов эхозапроса), время ожидания сообщения эхоответа и длину каждого пакета в байтах.

Подход к формированию значения метрики сетевого маршрута

Количество пакетов эхозапроса задается ключами [-c] или [/n]; граничное значение временной задержки указывается ключами [–W] или [/w] с аргументом «время ожидания в миллисекундах»; количество байт в пакете эхозапроса – ключами [-s] или [/l] для ОС семейств Linux и Windows соответственно. Таким образом, получение статистических данных о реактивности каждого из маршрутов на протяжении определенного (назначенного) временного интервала – достаточно рутинная задача.

Суточный интервал может быть разбит на подынтервалы, на которых собраны статистические данные о реактивности маршрутов, например, путем посылки серии ping-пакетов в начале и средине каждого часа. Полученные данные о количестве недоставленных пакетов (отказов) на каждом подынтервале позволяют построить гистограммы, отображающие количество отказов по ping-запросам в течение суток для каждого альтернативного маршрута.

Каждая из гистограмм может быть приближенно (регрессионный анализ) описана непрерывным закон распределения количества потерянных пакетов (граничных временных задержек) на всем временном интервале. В качестве примера рассмотрим графическую иллюстрацию двух вариантов законов распределения количества потерянных пакетов для двух маршрутов (см. Рисунок 1):

• •    равномерный закон распределения количества потерянных пакетов в течение суток с плотностью распределения f₁(t) = 1/t₄, условно – маршрут 1 ;

• •    нормальный закон распределения количества потерянных пакетов с плотностью рас-

• 1        (t - M (t ))2

пределения f₂(t) = ,— e ^2a   , математическим ожиданием М(t) и среднеквадрати-

V 2пст ческим отклонением σ = 1, условно – маршрут 2.

Плотность распределения характеризует количество потерянных пакетов (сообщений «превышен интервал ожидания для запроса») на каждом тестовом подынтервале для каждого маршрута.

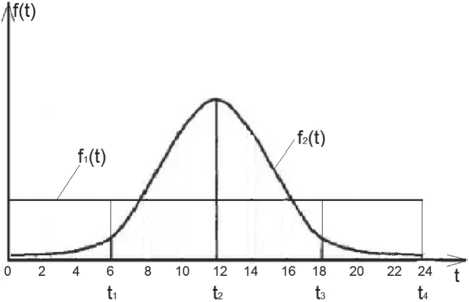
Рисунок 1. Законы распределения количества потерянных пакетов по двум альтернативным маршрутам

Условием нормировки является равенство площадей подкривых 1 и 2 плотностей рас-

24                  24

пределения f₁(t)иf₂(t): S 1 = S 2 = 1, где S 1 = J f 1 ( x ) dx и S 2 = J f ₂ ( x ) dx [3].

Таким образом, в формализованном виде задача назначения величин L метрик сетевых маршрутов как задача ранжирования площадей S подкривых плотностей распределения количества потерянных пакетов для соответствующих маршрутов примет вид arg minL (Si) e {S.|VS , i,k = 1..n, k ^ i: L(S ) > L(S.)},

Si где L(Si), L(Sk) – значения метрик i-го и k-го альтернативных маршрутов, назначаемые в каждом интервале; n – количество альтернативных сетевых маршрутов.

Определение метрик маршрутов

Формирование величин метрик выполняется путем сравнения площадей подкривых [1], образованных плотностями распределений количества потерянных пакетов. Чем меньше площадь подкривой плотности распределения на одинаковом временном интервале, тем меньшая временная задержка прохождения пакетов по маршруту, соответствующему этой плотности распределения.

Для иллюстрации формирования величин метрик рассмотрим четыре равных (четверть суток) временных фрагмента: 0–t1, t1–t2, t2–t3 и t3–t4. Тогда при вышепринятых законах распределения визуальное сравнение площадей на первом и четвертом фрагментах говорит о том, что метрика для маршрута, у которого плотность распределения количества потерянных пакетов подчиняется нормальному закону, меньше метрики маршрута, у которого плотность распределения подчиняется равномерному закону. Следовательно, для этих временных фрагментов в качестве основного сетевого маршрута предпочтительнее выбирать маршрут 2. И наоборот, для второго и третьего временных фрагментов сравнение площадей подкривых позволяет сделать вывод, что в качестве основного сетевого маршрута предпочтительнее выбирать маршрут 1.

В аналитическом виде выражения для площадей подкривых по каждому из четырех фрагментов для равномерного распределения примут вид t1                                                      ' 2                                                               ,

S ,^0-1 = [ / 1 ( x ) dx  = - ; S ,^1-2 = [ / 1 ( x ) dx  = —- ; S ,^2-3 = -—² ; S ,^3-4 = ——-

₀                 t _{4             t}                     t ₄                  t ₄                   t ₄

аналогичные выражения для нормального распределения запишем в виде [4]

^S2- =

2П

t j ^x-       1

[e ² dx = —

2 t i

/

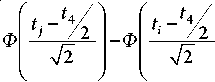
где i, j – нижний и верхний индексы границ соответствующего фрагмента, i = 0,

,3, j = 1,

(

…, 4; соответственно, Ô

t

. , ^'^

– функции Лапласа.

7             7

Нижний индекс в записи символа площади указывает на номер маршрута (закона рас- пределения).

Вычислим площади подкривых каждого из распределений для указанных четырех временных фрагментов.

Для равномерного распределения площади подкривой плотности распределения количества потерянных пакетов для всех четырех фрагментов одинаковы и равны L(S1) = 0,25.

Для симметричного нормального распределения с параметрами M(t) при t = t4/2 и σ = 1 площади подкривых на втором и третьем фрагментах будут равны L(S21-2) = L(S22-

Подход к формированию значения метрики сетевого маршрута

• ³) ≈ 0,43 (1,5 σ в каждую сторону от центра распределения), а на первом и четвертом – L(S₂^0-1) = L(S₂^3-4) ≈ 0,069, что подтверждает выполненное выше визуальное сравнение площадей и следующий из этого вывод.

Смену маршрута на каждом временном фрагменте можно выполнять путем установки актуальной метрики маршрута (команда route change…).

Заключение

Рассмотрен подход к формированию величин метрик для альтернативных сетевых маршрутов информационно-вычислительных сетей, который основан на анализе реактивности каждого из альтернативных маршрутов, полученной из статистических данных о количестве потерянных пакетов в течение определенного временного интервала и выводов в виде сформированных для них метрик.

Рассмотренный подход позволяет автоматически ранжировать маршруты по степени их предпочтительности и исключает при этом элемент субъективности.