Подход к математическому моделированию производства на авиастроительном предприятии на основе развития метода сетевого планирования управления

Оптимизация использования ресурсов при выполнении комплексов работ является общей задачей, для решения которой разработано множество достаточно строгих методов решения. Одной из наиболее удачных реализацией является метод сетевого планирования, который был разработан в 60-х годах прошлого века и был оптимизирован для существовавшей советской системы плановой экономики. Однако в настоящее время использование подобных средств на крупном самолетостроительном предприятии затруднено вследствие сложного характера связей между параметрами ресурсов предприятия и показателями его функционирования, особенно в условиях неопределенностей, например, таких как неизвестное количество самолетов в партии заказа или отсутствие четко формализованных связей между производством изделий разных типов. Авторами предлагается подход к построению математических моделей авиастроительных предприятий, основанный на развитии метода сетевого планирования управления.

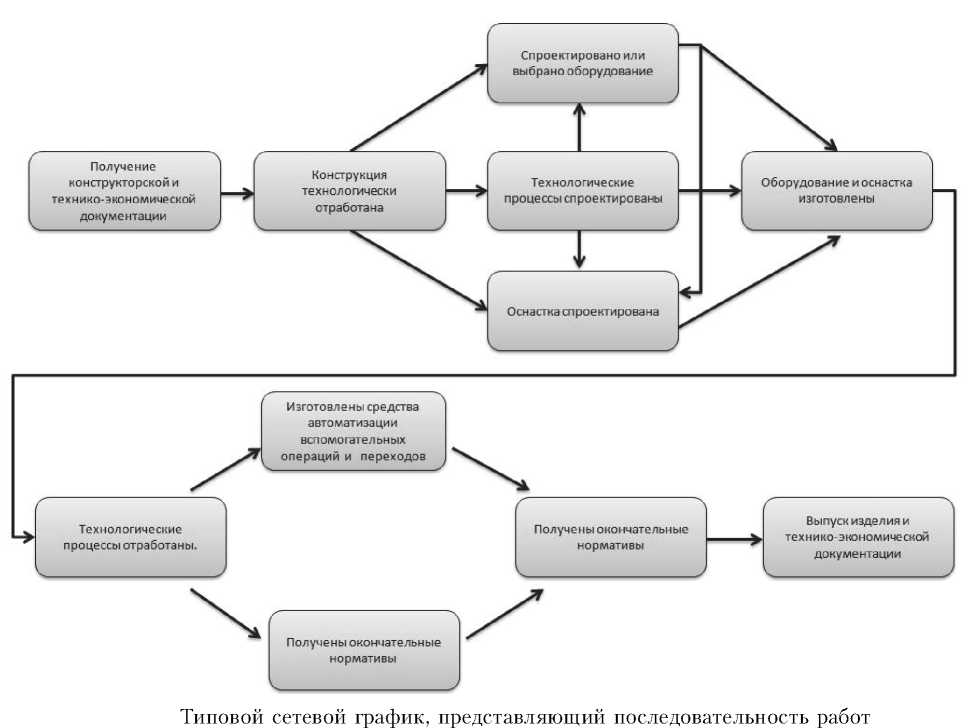
Предприятие производит и ремонтирует самолеты определенных типов. В соответствии с производственной программой можно выделить целенаправленные комплексы работ, которые можно описать с помощью раздельных сетевых моделей. В типовом графике (рис. 1) показаны укрупненные работы, характеризующие процесс подготовки к запуску нового изделия. Подобные этапы в реальном графике расписываются до конкретного исполнителя. Обычно для упрощения планирования и управления сетевой моделью осуществляют переход от непрерывного модельного времени к дискретному. Однако раздельное рассмотрение такого рода моделей несет в себе предпосылки того, что производство, организованное по оптимизированным частным моделям, будет далеко не оптимальным в целом. По большому счету это определяется тем, что между ком-

Чоракаев Олег Эдуардович, аспирант.

плексами работ возникает конкуренция за динамически распределяемые ресурсы, которая влияет на сроки выполнения работ по разным программам. В то же время обеспечение комплекса работ статически (т.е. постоянно на протяжении всего процесса) всем комплектом ресурсов не оправдано по экономическим соображениям.

Реализация каждого комплекса работ осуществляется выполнением определенного множества технологических процессов. Связь понятия «работа» в теории сетевого планирования и «технологический процесс» в организации производства очевидна. Технологический процесс содержит в себе информацию о ресурсах, необходимых для выполнения работы, он может быть оценен экономически, определяется время на его выполнение. Важно отметить то, что работа должна быть реализована.

Смысл предлагаемого метода заключается в том, что взаимосвязанный комплект исполнителей, оборудования, оснастки, деталей и материалов, обеспечивающий выполнение технологического процесса, объединяется как понятие рабочего места. Т.е. рабочее место – это комбинация необходимых названных ресурсов, которая обеспечивает выполнение работы с той или иной эффективностью. Другие ресурсы, такие как энергия, финансовые средства, производственные площади и т.д. учитываются опосредовано. Важно отметить, что элемент модели «рабочее место» создается под конкретный технологический процесс, а работа как отдельная часть производства может быть выполнена различными технологическими процессами, на разных «рабочих местах».

Рабочие места можно представить вершинами графа G(V,L), соединенными дугами – переходами. V – множество вершин, L –множество ребер или дуг. В целом граф является ориентированным, так как работы выполняются в определенной последовательности и частично связанным, так как из множества «рабочих мест», предусмотренных для выполнения конкретной работы дугами, будет связана лишь одна вершина. Вход дуги в вершину означает выполнение ра-

при технологической подготовке производства

боты. Пример графа представлен на рис. 2. Граф G таким образом отображает выполнение некоторого множества комплексов работ за достаточно большой (пусть год) промежуток времени.

В существующей системе подготовки производства достаточно хорошо отработаны вопросы оценки эффективности и оптимизации одиночного технологического процесса (рис. 3), что позволяет получить выигрыш в рамках крупносерийных производств. Но в рамках существующего авиационного производства, в условиях интенсивного движения ресурсов по своим траекториям, задаваемыми «рабочими местами», к себестоимости реализуемого технологического процесса необходимо прибавить стоимости переводов отдельных ресурсов из предыдущих вершин графа G (из пре-

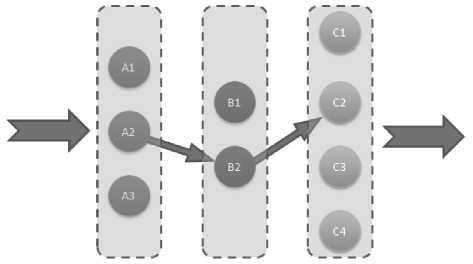
Рис. 2. Граф G(9,2), отражающий 2 работы, 9 рабочих мест в 3 множествах дыдущих «рабочих мест») в заданную вершину, где и происходит реализация заданного технологического процесса (рис. 4).

Именно эти дополнительные расходы не позволяют говорить об оптимальности производства в целом, даже если оптимизированы отдельные комплексы работ. Проекция работ из всего множества комплексов работ (рис. 5) на имеющиеся у предприятия ресурсы позволяет построить матрицу проекций работ, таблицу, в которой конкретная единичная работа выступает как название строки, а названиями столбцов выступают отдельные ресурсы и группы отдельных ресурсов. Элементами таблицы выступают значения признака возможности использования отдельных ресурсов в отношении различных работ. Значение признака равно 1, если ресурс может быть задействован для данной работы, или 0, если ресурс нельзя (нецелесообразно) задействовать (рис. 6).

На основе разрешенных комбинаций ресурсов со значением признака «может быть использован» по строке работы можно строить различные варианты технологического процесса выполнения работы (рис. 7). Каждый вариант будет задавать свою вершину графа G. Среди них обязательно будет и применяемый в настоящее время на предприятии. Одним из параметров вершины является время выполнения связанного с ней технологического процесса. Общее количество вершин V определяет размерность модели. Для предлагаемого метода моделирования про-

№р	Предш. ресурсы	Оборудование				Оснастка				Персонал
		1	1			1	1			1	1
		1						1		1
1.3			1				1				1	1
1.4	1.1, 1.2			1					1		1	1
	1.3		1				1			1	1
	1.3				1				1			1
	1.4, 1.5	1	1			1		1		1		1
	1.6				1			1			1	1
		1	1				1	1		1	1
		1	1			1				1	1
2.3	2.2			1					1			1
2.4	2.2		1	1			1	1	1		1	1
	2.1, 2.3				1			1				1
	2.3, 2.4				1				1		1

Рис. 6. Пример матрицы проекции работ

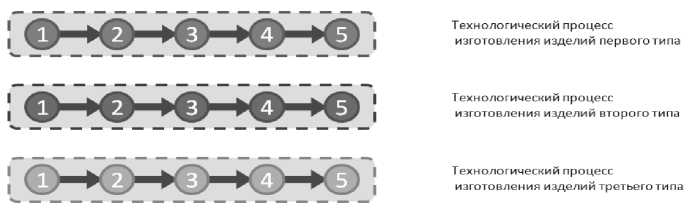
Рис. 3. Оптимизация единичных технологических процессов в рамках серийного производства

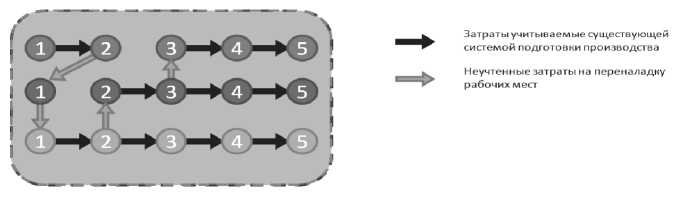
Рис. 4. Реализуемый технологический процесс в рамках существующего авиационного производства.

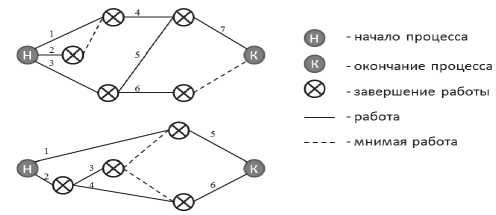
Рис. 5. Технологические процессы изготовления двух видов изделий на предприятии

изводства важно иметь оценку себестоимости каждого варианта технологического процесса выполнения работы. При применении метода существующие САМ-системы позволяют осуществить быстрый переход от одного варианта технологического процесса к другому.

Следующим интегральным элементом модели должны быть матрицы перехода ресурсов. Это квадратные матрицы размером VxV. Для каждого ресурса необходимо строить столько матриц, сколько параметров перевода ресурса отслеживаться. Например, элементом одной матрицы является оценка стоимости перевода ресурса из одного «рабочего места» в другое для тех мест, где такой перевод возможен и очень большое число, отображающее невозможность перевода ресурса на то место, где использование этого ресурса не предусмотрено (рис. 8а). Элементом следующей матрицы является время перевода. Там, где перевод невозможен, ставится очень большое время (рис. 8б). Например, перевод ресурса реально может быть связан с установкой стапеля, перезагрузкой программы на станке, получением отдельным рабочим или бригадой нового задания.

Не вызывает сомнений тот факт, что у различных однотипных ресурсов, которые могут использоваться для реализации технологического процесса, различные показатели «эффектив-ность/стоимость». При расчете сетевых моделей задействованный в одном комплексе работ ре-

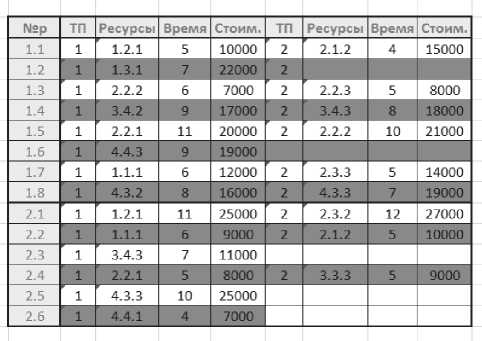
Рис. 7. Совокупность различных вариантов техпроцесса выполнения работы

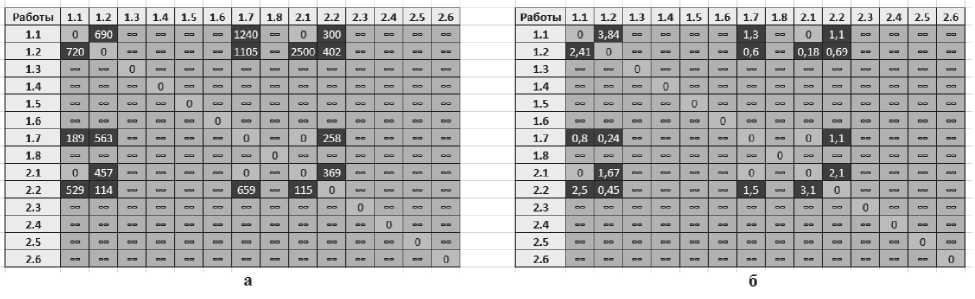
Рис. 8. Матрицы перевода ресурсов по стоимости (а), по времени (б)

сурс не может быть использован в то же самое время в рамках других комплексов. Это вызывает необходимость задействовать менее эффективные ресурсы. Подход предполагает поиск таких распределений ресурсов, которые делают более оптимальным всё производство в целом.

Концептуально матрицы проекций работ и перевода ресурсов являются динамическими. Они могут быть изменены в любое время. И шаги моделирования производства будут заключаться в выборе оптимальной по определенному критерию следующей вершины («рабочего места») с учетом возможности ее включения, определяемого возможностью выделения в данный момент определенных вершиной ресурсов.

Существует множество факторов, негативно влияющих на производство. Это поломки оборудования, ошибки персонала, перебои в снабжении, болезни сотрудников, неблагоприятные погодные и другие условия, запланировать которые невозможно. Но можно учесть их влияние на производство на основе статистики. Предприятие имеет определенную статистику по основным факторам, влияющим на производство. Использование этой статистики в рамках предлагаемой модели позволит получить более реалистичные оценки показателей выполнения комплексов работ. Причем этот учет будет не грубым с погрешностью десятков процентов, а более точным с погрешностью в единицы процентов. Основная идея использования статистики предприятия заключается в моделировании производства с учетом случайного воздействия на конкретные ресурсы, причем законы этого воздействия задаются на основе имеющейся статистики. Многократный прогон модели позволит получить статистически обоснованные оценки общих показателей производства.

У авторов в настоящий момент имеются идеи относительно алгоритмов оптимизации, но они требуют дополнительной проработки. Особенно это касается решения задач очень большой размерности.

Предлагаемая модель может быть использована как на этапе планирования, так и на этапе оперативного управления. Во втором случае в матрицы проекций и переводов необходимо внести данные, соответствующие возникшей производственной ситуации и произвести оптимизацию по «невыполненной» части графа. Это позволит получить те изменения первоначальных планов, которые позволят наиболее эффективно разрешить возникшую проблему.