Подход к моделированию динамики процесса раскрытия крупногабаритных солнечных батарей космических аппаратов

Система энергообеспечения — одна из наиболее важных систем космического объекта (КО) (пилотируемого или грузового корабля, автоматического космического аппарата, орбитальной станции, межорбитального буксира), от надежности которой зависит, сможет ли КО выполнить свою долгосрочную миссию [1–7].

После вывода на целевую орбиту внутренние источники энергии могут поддерживать функционирование КО в течение короткого промежутка времени

(нескольких часов), после чего наступают необратимые изменения, приводящие к деградации систем КО и его потере. Внешним источником энергии для КО являются солнечные батареи (СБ). На участке выведения они зафиксированы в компактном транспортировочном положении, позволяющем разместить их в ограниченном объеме под обтекателем. Для обеспечения внешнего притока энергии к КО необходимо осуществить их раскрытие. Таким образом, процесс раскрытия СБ становится одной из ключевых динамических операций, что предъявляет высокие требования к обоснованности выбора характеристик элементов системы раскрытия.

На ранних стадиях проектирования СБ рассматривается целый ряд кинематических схем раскрытия, типов механических связей между элементами СБ (панелями, рамами, штангами), конфигурации самой батареи и т. д. На поздних стадиях, при наземной отработке системы раскрытия СБ на стендах, условия невесомости, как правило, воспроизводятся путем обезвешивания каждого элемента СБ с помощью блочно-тросовой системы. Фрагмент корпуса КО жестко крепится к полу, поэтому зафиксировать угловые возмущения, получаемые КО при раскрытии СБ, не представляется возможным. Воспроизведение на стенде нештатных ситуаций раскрытия также проблематично [8, 9]. В связи с этим, основным способом подтверждения правильности принимаемых технических решений является детальное математическое моделирование процесса раскрытия СБ.

Модель механической системы

Известны различные конструкции и схемы раскрытия СБ.

Батареи очень большой площади предназначены для обеспечения энергией орбитальных станций. Они выполняются по рулонной технологии, позволяющей достичь высокой удельной мощности (200–500 Вт/кг). Солнечные батареи транспортных пилотируемых или грузовых кораблей, автоматических космических аппаратов (АКА) изготавливаются с жесткими раскрываемыми панелями.

Простейшие кинематические схемы раскрытия [10] (однофазные схемы) предполагают прямой перевод СБ из транспортировочного положения в рабочее

(рис. 1, а ). В связи с существующей тенденцией резкого увеличения энергопотребления и соответствующим ростом размеров самой СБ все чаще используются более сложные (многофазные) схемы раскрытия [10, 11], при которых существует одно (рис. 1, в ) или несколько (рис. 1, б ) промежуточных фиксированных положений. В первой фазе раскрытия осуществляется разворот целого пакета панелей до некоторого фиксированного положения, относительно которого происходит дальнейшее движение, и так до полного раскрытия СБ.

В исходном (транспортировочном) положении СБ компактно сложены и зафиксированы на корпусе автоматического космического аппарата (АКА). При раскрытии батареи происходит расфикса-ция, перевод батареи в конечное (рабочее) положение и фиксация батареи в нем. Поэтому система раскрытия включает в себя следующие структурные элементы:

• •    средства фиксации в транспортировочном положении, которые при подаче соответствующей команды снимают наложенные механические ограничения, разрешая относительное движение элементов батареи (панелей, рам, штанг). В качестве средств фиксации часто используются пирозамки [12];

• •    средства инициации разворота элементов батареи. Относительный разворот пары панелей СБ, как правило, осуществляется пружинами кручения, установленными на оси вращения. Для преодоления на начальном участке сил трения используются короткоходовые пружинные толкатели [12];

• •    средства фиксации батареи в раскрытом (рабочем) положении выполняются в виде устройства замкового типа.

Кроме того, на современных СБ применяются дополнительные средства:

• •    средства тросовой синхронизации относительного углового движения соседних пар элементов СБ. Устройство синхронизации ускоряет разворот «отстающей» пары элементов СБ и одновременно тормозит «спешащую» пару. Оно представляет собой замкнутый подпружиненный (для компенсации температурных деформаций) трос, переброшенный через два шкива, принадлежащих расположенным через один элементам СБ. Применение тросовой синхронизации позволяет снизить нагрузки на элементы батареи и повысить надежность системы

раскрытия, благодаря возможности осуществления процесса раскрытия даже при отказе одной из пружин кручения, установленных в осях разворота;

• •    средства торможения (демпферы), гасящие относительную угловую скорость пары соседних элементов батарей перед фиксацией их в рабочем конечном положении с целью снижения ударных нагрузок в момент фиксаций.

Подходы к математическому моделированию процесса раскрытия СБ основываются, как правило, на методах аналитической механики, с максимальным учетом конкретных особенностей моделируемой системы — конструкции СБ, кинематической схемы ее раскрытия, средств инициации разворота панелей, свойств отдельных элементов конструкции СБ и т. д. [11, 13–21].

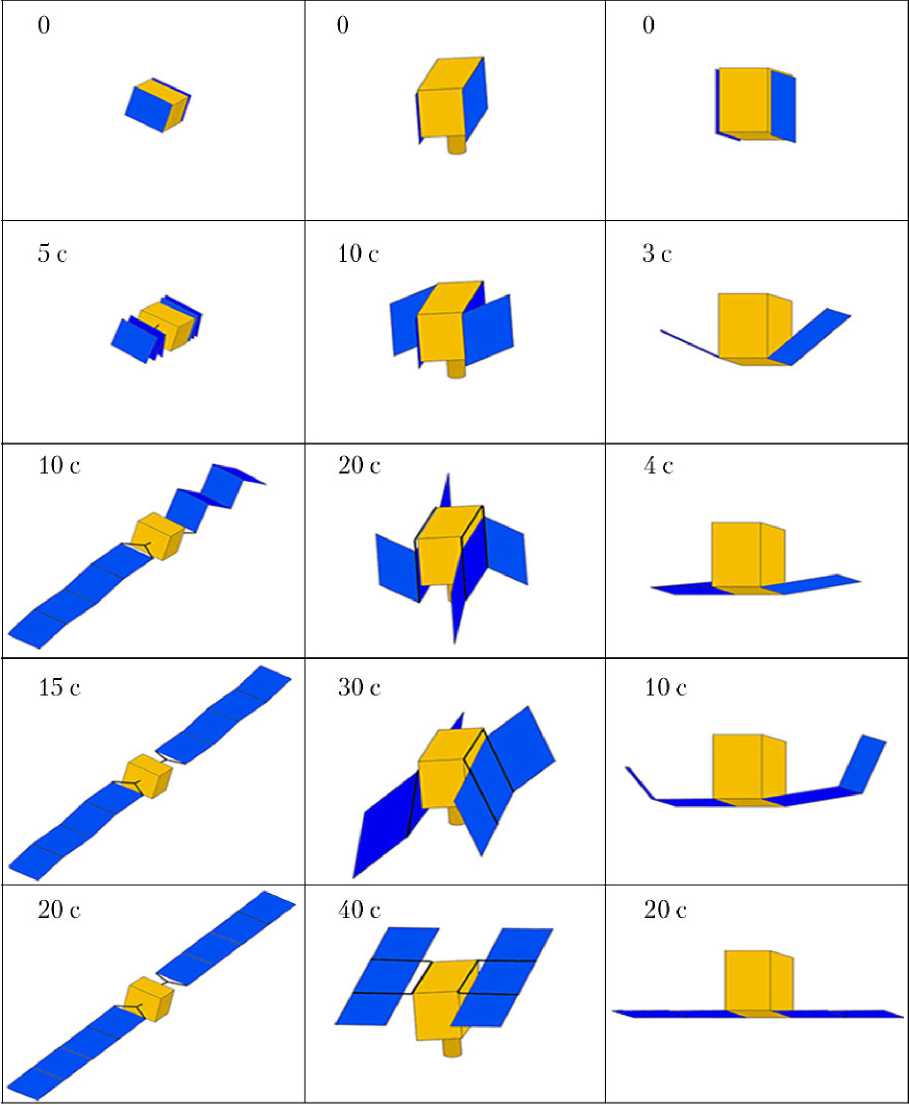
б)

а)

в)

Рис. 1. Кинематические схемы раскрытия солнечных батарей: а — аппараты типа «Ямал» (однофазная схема); б — «Н»-образная схема (трехфазная схема); в — аппарат «БелКА» (двухфазная схема)

Можно использовать уравнения Лагранжа 2-го рода. Для ряда существующих (чаще всего, однофазных) схем такой подход позволяет получить систему уравнений движения минимальной размерности, равной имеющемуся числу степеней свободы системы [22, 23]. Однако реализация этого подхода для описания раскрытия крупногабаритных батарей имеет ряд трудностей. При моделировании многофазных схем в процессе раскрытия общее число степеней свободы системы меняется (увеличивается), поскольку для каждой новой фазы характерно снятие дополнительных связей. Таким образом, для каждой новой фазы необходимо заново составлять систему уравнений движения (вводить соответствующую ей дополнительную обобщенную координату), аналитически переопределять кинетическую энергию системы и обобщенные силы в соответствии с появившимися степенями свободы. Это расширяет размерность неразвязанной системы уравнений движения и увеличивает трудоемкость ее решения. Кроме того, в рамках такого подхода невозможно напрямую определить реакции в узлах разворота элементов СБ, что является одной из главных целей расчета.

Представляется целесообразной разработка подхода, который включал бы универсальное формирование расчетной модели на базе парциальных геометрических и инерционных характеристик каждого тела системы, удобного для разработки эффективных численных алгоритмов и высокоскоростных программных реализаций.

Предлагаемый подход основан на представлении конструкции КА и СБ как пространственной структурно-сложной системы тел, совершающих относительное движение под действием специфических силовых факторов. Подход справедлив для случая, когда панели СБ представляют собой жесткие конструкции и рассматриваются как твердые тела. Учет упругих свойств элементов СБ (когда это необходимо) — самостоятельная проблема, не затрагиваемая в данной статье.

Метод описания динамики процесса раскрытия предполагает разбиение механической системы на отдельные тела (корпус КА, элементы СБ). Для каждого тела системы записываются уравнения движения центра масс и уравнения пространственного вращения относительно центра масс на основе общих теорем динамики. Записываются кинематические соотношения, позволяющие определить компоненты матриц линейного преобразования систем координат, которые вводятся для описания абсолютного и относительного движений рассматриваемых тел. Для определения сил и моментов реакций связей, действующих на данное выделенное тело со стороны других тел, составляется специальная система уравнений связей. Система динамических уравнений движения, кинематических уравнений и уравнений связей решается совместно. Для ее решения существуют численные методы, учитывающие специфику исследуемого процесса.

При предложенном подходе для многофазных схем раскрытия появление каждой новой степени свободы означает снятие ограничений по соответствующей этой степени свободы координате и обнуление проекции силы или момента реакции связи.

Возможности рассматриваемого подхода проиллюстрированы на примере схемы раскрытия СБ типа «гармошка» (см. рис. 1, а ) [10, 11]. Такая схема реализована, например, на АКА серии «Ямал», а также некоторых других (рис. 2).

Уравнения поступательного перемещения центра масс каждого тела рассматриваемой механической системы и уравнения вращательного движения относительно центра масс, соответственно, будут иметь вид:

m _i a _i = F _{0 i} + R _i ; (1)

[ I _{0 i} ] ε _i + ω _i × ([ I _{0 i} ] ω _i ) = L _{0 i} + L _i + L ( R _i ) _ci , (2)

где a _i и ε _i — ускорение центра масс и угловое ускорение i -го тела системы, соответственно; m _i и [ I _{0 i} ] — масса и тензор инерции i -го тела, соответственно; ω _i — угловая скорость тела; F _{0 i} — главный вектор внешних сил; R _i — главный вектор сил реакций связей, действующих на i -е тело; L _{0 i} — главный момент внешних сил; L _i — главный момент связей; L ( R _i ) _ci — главный момент сил реакций связей.

Уравнения движения (1) и (2) не могут быть сразу проинтегрированы, поскольку, кроме внешних сил и моментов, создаваемых средствами раскрытия, в них входят неизвестные силы и моменты реакций связи. Для их определения система дифференциальных уравнений (1) и (2) дополняется специальными уравнениями связей. Вид и структура уравнений связи определяется конкретным видом связи — теми ограничениями, которые накладывает связь на относительное движение тел. Наиболее часто встречающийся в кинематических схемах раскрытия СБ тип связи — ось вращения (рис. 3), однако возможны связи, допускающие относительное линейное перемещение либо комбинацию линейных и угловых перемещений (например, шарнир с проскальзыванием).

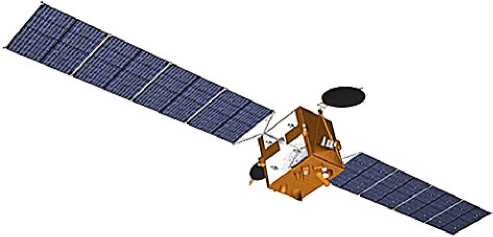
а)

б)

Рис. 2. Общий вид космического аппарата с солнечными батареями: а — рабочее положение; б — транспортировочное положение

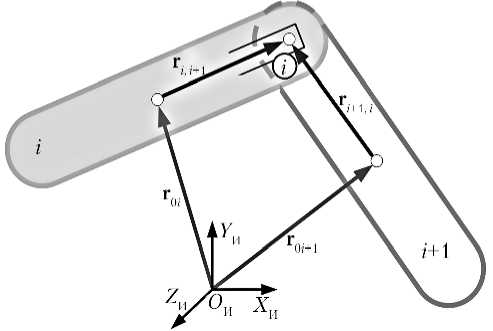
Рис. 3. Схема соединения взаимодействующих тел

Запишем универсальные уравнения связей для двух тел, в предположении, что связь в общей контактной точке i -го и ( i +1)-го тел допускает, в общем случае, и линейные, и угловые степени свободы (рис. 3).

r _{0 i} + r _{i,i +1} = r _{0 i +1} + r _{i +1, i} ; (3)

ω _i – ω _{i +1} = 0, (4)

где r _{0 i} и r _{0 i +1} — радиус-векторы, определяющие положение центров масс взаимодействующих тел в инерциальной системе координат; r _{i,i +1} и r _{i +1 ,i} — векторы, определяющие положение точки контакта в связанных системах координат, причем один из них (для определенности r _{i,i +1}) меняется также и по модулю. В двойной индексации векторов r _{ii +1} и r _{i +1 i} первый индекс — это индекс тела, в связанной системе координат которого этот вектор определен; второй — индекс того тела, с которым данное тело взаимодействует.

После двойного дифференцирования выражения (3) и (4) приобретают, соответственно, вид (5) и (6).

a _i + ε _i × r _{i,i +1} + ω _i × ( ω _i × r _{i,i +1}) +

+2 ω _i × V _{i,i +1} + a _{i,i +1} = a _{i +1}+ ε _{i +1} × r _{i +1, i} + + ω _{i +1} × ( ω _{i +1} × r _{i +1 ,i} ); (5)

ε _i – ε _{i +1} + ω _i × ω _{i +1} = 0, (6)

где V _{i,i +1} — относительная линейная скорость двух тел в точке связи; a _{ii +1} — локальное (в связанной системе координат i -го тела) ускорение точки контакта.

Подстановка a _i и ε _i из уравнений (1), (2) в соотношения (5), (6) приводит к системе матрично-векторных уравнений относительно неизвестных компонент сил и моментов реакций связей каждой пары элементов солнечных батарей, окончательный вид которой не приводится из-за громоздкости.

Покажем итоговую структуру матрицы коэффициентов уравнений связи применительно к процессу раскрытия СБ КА типа «Ямал». Механическая система состоит из 11 тел — корпуса и двух «крыльев» СБ ( k = 1, 2 — число «крыльев»), по пять тел ( i = 5) в каждом «крыле» — четыре панели и штанга (рис. 2). Таким образом, в системе имеется 10 связей в виде осей вращения.

Неизвестные силы и моменты реакций связей в точках контакта соседних элементов СБ (панелей) показаны на рис. 4.

(/+2)-я панель

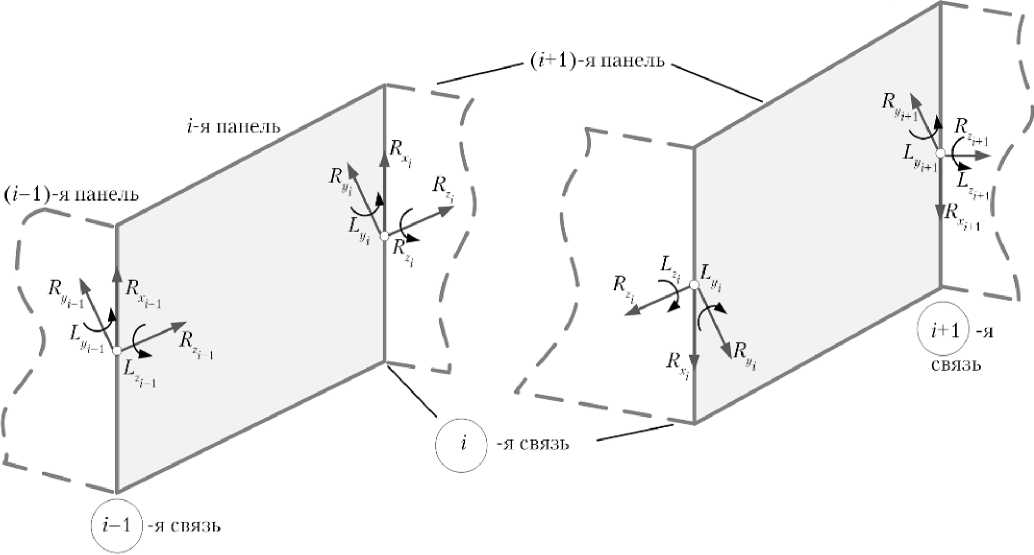
Рис. 4. Силовые факторы в точках контакта элементов солнечных батарей

Для связи типа оси вращения в выражении (5) в левой части равенства два последних слагаемых равны нулю, а векторное равенство (6) проектируется на две оси, ортогональные оси относительного разворота панелей. Подстановка ускорений центров масс и угловых ускорений из уравнений (1) и (2) в выражения (5), (6) дают пять скалярных уравнений для каждой из связей, в которые, помимо реакций данной связи, входят силы и моменты как предыдущей, так и последующей связей.

В общем виде полученные уравнения связи могут быть записаны следующим образом:

[ A ^R i –1 ] R ^C i –1 + [ A ^R i ] R ^C i + [ A ^R i +1 ] R ^C i +1 +

+ [ A i ^L –1 ] L ^C i –1 +[ A i ^L ] L ^C i + [ A i ^L +1 ] L ^C i +1 = B i ;

[ C ^R _{i –1}] R ^C _i–1 + [ C ^R _i ] R ^C _i +[ C ^R _{i +1}] R ^C _{i +1} +

+[ C i ^L –1 ] L ^C i –1 +[ C i ^L ] L ^C i + [ C i ^L +1 ] L ^C i +1 = D i ;

где [ A ] и [ C ] — матрицы коэффициентов при соответствующих компонентах сил и моментов реакций связей; B и D — векторы-столбцы свободных членов.

Уравнения связи в виде (7) и (8) справедливы для всех связей в k -м крыле, за исключением первой ( i = 1) и последней ( i = I _k , в нашем случае i = 5).

Для i = I k R ^C k,i +1 = 0; L ^C k,i +1 = 0.

Для первого тела (корпуса) главный вектор и главный момент первой связи (со штангами) получаются суммированием по числу крыльев, т. е. для k -го крыла при индексе связи i = 1 уравнения связи будут иметь вид:

2 и A yR C i + [ A yR C 2 +

+ ^k [ A ^L ] L ^C + [ A ^L ] L ^C = B ; k =1 k 1 k 1          k 2 k 2        k 1

• 2 и C yR C , 1 + [ C yR C 2 +

• ■ 2 и C L , 1 ] L C i + [ cyL C ,2 = D ,1 -

• Таким образом, матрица коэффициентов уравнений связи будет иметь размерность 50 x 50.

На рис. 5 подробно показана покомпонентная структура характерного фрагмента матрицы, показанной на рис. 6.

s 8 эЯ s		R 1			L 1
		x	y	z	y	z
	x
	y
	z
	y
	z

Рис. 5. Фрагмент матрицы коэффициентов

Первое крыло

Второе крыло

R 1

L 1

R 2

L 2

R 3

L 3

R 4

L 4

R 5

L 5

R 1

L 1

R 2

L 2

R 3

L 3

R 4

L 4

R 5

L 5

Уравнения 1-й связи

Уравнения 2-й связи

Уравнения 3-й связи

Уравнения 4-й связи

Уравнения 5-й связи

Уравнения 1-й связи

Уравнения 2-й связи

Уравнения 3-й связи

Уравнения 4-й связи

Уравнения 5-й связи

Рис. 6. Структура матрицы коэффициентов уравнений связи. ■ — ненулевые коэффициенты матрицы

Интегральные характеристики процесса раскрытия

Предложенный подход позволяет определить основные интегральные параметры процесса раскрытия СБ: зависимость углов разворота и угловых скоростей панелей и штанг от времени; последовательность фиксации элементов СБ; время процесса раскрытия и др. Числовые коэффициенты (жесткость и вязкость фиксаторов, жесткость и вязкость тросов системы синхронизации и др.) задаются как набор внешних исходных данных, подлежащих уточнению при экспериментальной отработке.

На рис. 7–10 приведены основные параметры процесса раскрытия СБ, состоящей из двух идентичных «крыльев».

На рис. 7 можно выделить характерные области: короткий начальный участок роста энергии, обусловленный работой короткоходовых толкателей, инициирующих процесс раскрытия; равномерный рост энергии вследствие работы пружин кручения; участок спада — срабатывание механизмов фиксации панелей; затухающие вследствие диссипации остаточные колебания, от длительности которых зависит время, отводимое на процесс раскрытия батарей в общей программе динамических операций КА на орбите.

Е, Нм

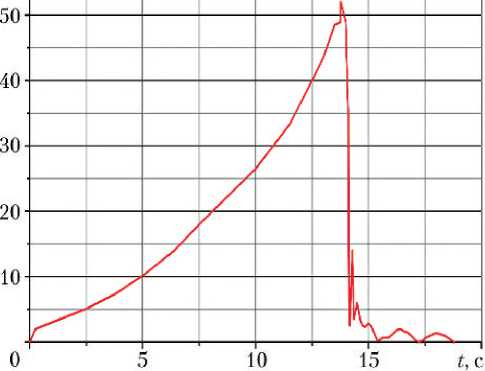
Рис. 7. Изменение энергии системы по времени

На рис. 8 момент выхода относительных углов на конечное значение соответствует моменту фиксации данной пары панелей.

Интенсивные колебания угловой скорости панелей в процессе фиксации (рис. 9) объясняются ударным характером фиксации. Большей плавности процесса и снижения уровня нагружения можно добиться использованием демпфирующих устройств.

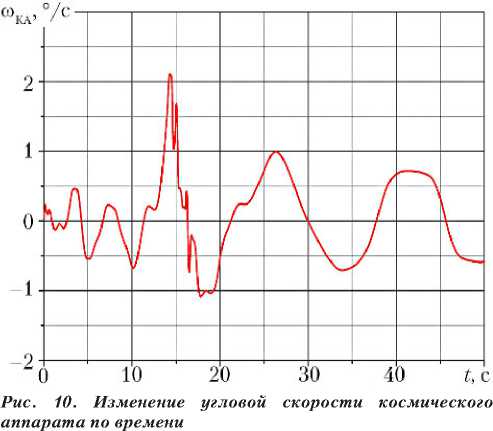
Угловое возмущение КА в плоскости раскрытия СБ показано на рис. 10.

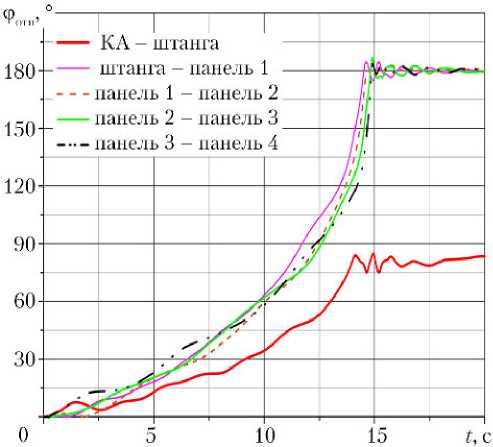
Рис. 8. Изменение относительных углов раскрытия элементов солнечных батарей по времени

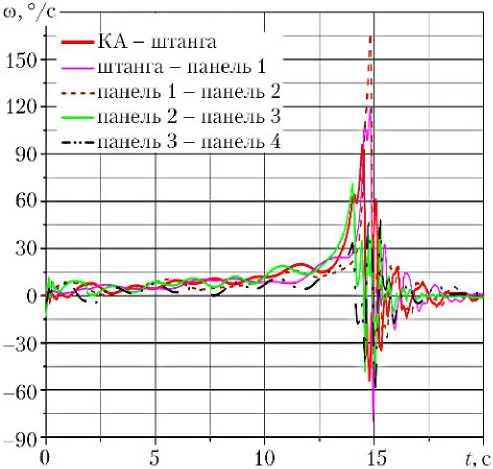
Рис. 9. Изменение относительных угловых скоростей раскрытия элементов солнечных батарей по времени

Кроме того, могут быть вычислены усилия и моменты в тросах системы синхронизации, реакции в узлах разворота и ряд других параметров.

Выводы

В рамках единого методического подхода предложена гибкая система моделирования процесса раскрытия крупногабаритных солнечных батарей, включающая метод формирования конкретных расчетных моделей, позволяющих проводить массовые расчеты в пространстве большого числа параметров.

Подход обладает хорошими адаптационными возможностями перспективных кинематических схем раскрытия СБ (см. рис. 1), включая многофазные схемы раскрытия, позволяет определять параметры абсолютного и относительного движений любого фрагмента системы, возмущения КА, вызванные процессом раскрытия, анализировать нештатные ситуации раскрытия.

Предполагается развитие предложенного в статье подхода к перспективным конструкциям СБ с новыми нестандартными типами развертывания (например, в виде оригами), отверждаемыми поверхностями и др.