Подход к обработке данных о воздушно космических групповых объектах в информационной системе с ограниченными возможностями

Пусть имеется сложная иерархическая информационная система S , осуществляющая отображение данных о воздушно-космических групповых объектах, действующих в зоне ее ответственности. Система включает технические и эргатические элементы. Совокупность технических элементов представлена измерительными элементами, каналами обмена информацией и средствами ее обработки:

S = U sn ’

N где n = [1, N] – n-й элемент системы.

Пусть X - универсальное множество объектов, действующих в границах зоны ответственности информационной системы. Элементом этого множества является отдельный объект х ∈ Х , который характеризуется векторами параметров ν, определяющих его положение в пространстве

параметров на момент времени t = [0, Т ] и признаков p , т. е. x = x i ( v , p , t ).

Тогда

X = U X i ( v , P , t ) ,

I где I - количество объектов, находящихся в границах зоны ответственности информационной системы, или мощность универсального множества Х, card X = I.

Осуществляя отображение обстановки в зоне ответственности, система воздействует на нее оператором R S , который в соответствии с [1] представляет собой системный оператор

Rs з Rs х S, s s sTp s s sTp s sTp s где R {^ an , pnq , pnq] G A х P х P •{ gnq   1, Xnq

= 1}, Vn = [1, N], q e Q} — оператор отображения об становки на sn-м элементе системы.

Том 2

Элементами кортежей, входящих во множество R^s , являются:

алгоритм a^s_n е A^s, принадлежащий подмножеству реализованных на элементе системы алгоритмов;

- потребные для его реализации вычислитель-sTp ные ресурсы по типам ресурсов pnq ;

– наличные ресурсы по типам ресурсов p_n^s_q .

Результатом воздействия оператора является множество X R , описывающее информацию об обстановке в зоне ответственности и представляющее собой отображение прообраза множества X :

X r = R s ({ X} ) = R s ({ J x( v , p, t )}) =

I

= UXRk (vR, pR, tR ), xRk G XR, I ^ K, X ^ XR, k xi (V, p, t) ^ xRk (VR, pR, tR), где card XR = K - мощность подмножества отображенных системой объектов, т.е. множество отметок от объектов, информация о которых отображается в системе сбора и обработки; к = [1, K] - номер объекта; ,xRk (vR, pR, tR) g XR - информация о к-м объекте, отображаемая в системе сбора и обработки.

В связи с тем, что элементы информационной системы обладают вполне определенными наличными ресурсами P s и характеризуют-ся соответствующей производительностью N's , в определенных условиях на различных уровнях системы возникает ситуация информационной перегрузки, когда количество объектов, информация о которых имеется на входах соответствующих элементов системы и потребителей информации превышает их возможности по обработке, т. е. card X R = K >  N’ s .

В условиях информационной перегрузки в системе происходят потери информации, т. е. данные о части объектов не поступают в систему сбора и обработки или определенному потребителю, увеличиваются задержки информации, она «стареет», ухудшается ее качество и соответствующим образом снижается эффективность информационной системы.

Цель исследования – предложить подход к минимизации потерь информации реального масштаба времени в условиях информационной перегрузки сложной иерархической системы с ограниченными возможностями на основе агрегирования данных об объектах, действующих компактными группами.

Пусть в зоне ответственности системы находится X множество объектов, действующих J компактными группами и решающих общую задачу Z . Общую задачу можно декомпозировать на совокупность частных задач, каждая из которых Z j решается группой или одиночным объектом:

Z = U Z j , j = [1, J ]•

J

Множество объектов X = { x i }, x i g X распределяется по J группам в соответствии с частными задачами:

x ij g X j , X j с X, X ^ Z, X j ^ z j , z j g Z•

Можно утверждать, что отдельные объекты в группе находятся между собой в определенном отношении, которое характеризует степень участия каждого из составляющих группу в решении общей ее задачи и взаимное отношение при ее решении между составляющими группу.

При выполнении задач множество объектов подвергается воздействию совокупности факторов Q (предсказуемых и непредсказуемых), изменяющих исходное их распределение по задачам и группам:

X х Q = X q , { X } x { q i } = X q , X q с X , q = [1, Q ].

Пусть φ: X_Q → X_Rs – заданное отображение, получаемое при воздействии оператора обработки R_S , а X_R – подмножество отметок от объектов, являющееся результатом обработки, т. е. обнаружения и оценки их кинематических параметров и приз_Тн_оа_гк_до_ав.

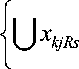
X R ^ Z R c Z, т.е.

> ^ U Z jRs , k = [1, K ], j = [1, J ]•

i

Рассмотрим, как отношение между объектами в группе отображается информационной системой.

Процесс отображения данных об обстановке связан с актуализацией целого ряда неопределенностей, имеющих различную природу. Процесс и результат отображения базируются на применении формальных и логических методов, специальных технических «языков», в которых используются системы цифровых кодов, бинарная логика, соответствующий алфавит символов и т.п., описывающих в информационной системе внешние воздействия. Этим языкам свойственна так называемая «омонимическая» или семантическая неопределенность. Поэтому одной из составляющих неопределенности является неопределенность, носящая лингвистический характер. Отображение отношения между объектами в группе и представление их в системе осуществляются с использованием «технического языка». В этом случае лингвистическая неопределенность доминирует в «свертке» неопределенностей, влияющих на результат отображения. В условиях временных ресурсных ограничений, отсутствия возможности точного определения решаемой группой задачи и ограничений, свойственных собственно использу- емым «языкам», их «алфавиту», неопределенность такого рода носит характер нечеткости. Поэтому для анализа процессов, происходящих при отображении отношений между объектами в группе в информационной системе в условиях временных и ресурсных ограничений, целесообразно использовать аппарат теории нечетких множеств.

Пусть X j - некоторое подмножество (группа объектов) множества Х , находящееся в определенном отношении, которое характеризуется функцией принадлежности μ( x ). В соответствии с принципом обобщения [2, 3, 4] образ X j при отображении ф определяется как нечеткое подмножество множества X jRs , представляющее собой совокупность пар вида

^XjRs = { ( x RS , ^Ц j ⁽ x Rs ) ) } ,

⁽ x_Rs, Ц j ^{( x} Rs )) = ⁽ ф ( x ) Ц ⁽ x )) x G X , где ц j : X jRs ^ [0,1] - функция принадлежности образа.

Функцию принадлежности ц k можно записать в виде

Ц k ( X r ) = sup ц ( x ), X r g X kR , x ^Л x R )

где множество φ^–1( х_R ) для любого фиксированного х_R ∈ Х_R имеет вид

φ–1(хR) = {х ∈ Х / φ(х) = хR}, т. е. представляет собой множество всех элементов х g Х, образом каждого из которых при отображении φ является элемент хR.

В случае нечеткого отображения

р : X ^ X R .

Описывается нечеткое отображение функцией вида

Ц.: X х XR . [0, 1], нечетким отношением R, причем значение μR(x, хR) определяет отношение отображения объекта x.

Функция ц _R ( x , x_R ) есть функция принадлежности нечеткого множества отображения в подмножество Х_R , представляющего собой нечеткий образ объекта x (т.е. нечеткое подмножество) при данном отображении.

То есть в ходе отображения информации в системе могут возникать ошибки, приводящие к дублированию, размножению данных и появлению ложной информации. Это, в свою очередь, также создает предпосылки для информационной перегрузки и увеличению потерь информации в системе.

Несмотря на возникающие при отображении ошибки, необходимо, чтобы отображение было адекватным или влияние ошибок и потерь информации при отображении в условиях временных и ресурсных ограничений было несущественным, т. е.

Z rs ^ Z .

По множеству отображаемых реальных и ложных отметок от объектов на различных уровнях информационной системы осуществля- ется оценка обстановки, определение совокуп- ности решаемых объектами и их группами задач U z'Rs с ZRs, формирование и выдача соответствующей информации потребителю для реализации своевременных и точных воздействий по объ-

ектам. Причем от адекватности, т. е. от полноты, точности и достоверности отображения, зависит степень достижения цели функционирования системы и надсистем, ею обеспечиваемых, или их качество и эффективность.

Если K - показатель качества или адекват- ности отображения обстановки в зоне ответствен- ности системы, то в соответствии с целевым предназначением информационной системы показатель эффективности системы можно представить следующим образом:

Э = f ( K ).

В условиях временных и ресурсных ограничений из-за информационной перегрузки и возникающих ошибок, потерь информации при отображении эффективность системы снижается.

Потери информации в системе сбора и обработки можно определить следующим образом: a = (1 – K ).

Основными направлениями, обеспечивающими сохранение требуемой эффективности системы в условиях информационной перегрузки и возникающих при этом потерь информации, являются: – повышение информационных возможностей системы за счет увеличения вычислительных возможностей технических средств;

– повышение информационных возможностей системы за счет реализации соответствующих алгоритмов обработки информации, обеспечивающих эффективное функционирование системы в условиях информационной перегрузки.

Наиболее привлекательным с экономической точки зрения [5, 6] является второе направление, в рамках которого один из возможных путей, снижающих остроту проблемы перегрузки, состоит в разработке и реализации в системе методов и алгоритмов обработки агрегирования, учитывающих групповые действия объектов при удовлетворении требований потребителей информации к ее качеству.

В формализованном виде это означает, что если множество X можно разбить на J непересека-ющихся подмножеств:

Том 2

X UXjAXj 0 Xj {x1j,x2j,-,xj}, то представление каждого подмножества Х, с X одним показателем xХГ = ф(Xj), ( = 1 J) и есть агрегирование информации.

Таким образом, для повышения эффективности системы в условиях информационной перегрузки множество методов агрегирования и обработки агрегированной информации А ₀, реализуемых в системе, должно обеспечить минимизацию потерь информации при удовлетворении требований к методу и потребителей информации к ее качеству:

А ⁰ = Arg min а ( A ) = { A е A _Q | а ( A ) =

A G A ₀

= mein а(A )} ’

®

a(А) = F(A, оs, Аs, Nj, Xr, 0), где 0 - множество требований к алгоритмам обработки информации; АΘ – множество методов, удовлетворяющих требованиям потребителей информации; a(А) = 1 – KА – потери информации в системе при выбранном множестве методов и алгоритмов агрегирования А; оS, АS, N 1 - точность, разрешающая способность и пропускная способность системы сбора и обработки информации о воздушной обстановке.

Для агрегирования информации при обеспечении минимизации ее потерь необходимо выделить некий агрегированный признак, характеризующий группы отметок - отображений объектов. Таким признаком для отдельной группы отметок может быть признак, характеризующий боевой порядок или взаимное расположение отметок в пространстве. Для его выделения необходимо формально описать боевой порядок группы отметок. Это можно сделать путем составления отношения, описывающего связи между объектами, характеризующие общность решаемых задач, в данном случае связи между отметками в группе.

Отношение является самой общей формой описания связей между объектами. Отношением, построенным на множестве объектов и групп объектов, можно характеризовать их распределение в пространстве параметров и признаков.

Обозначим это отношение символом К г и рассмотрим его на множестве Х_R .

Отношением К_г на множестве отображенных отметок от объектов Х_R представляет собой подмножество декартова произведения Х_К х Х_К . Задать отношение на множестве Х_К означает указать все пары элементов х , у е Х_К , такие, что х и у связаны отношением R_г , т. е. xR_г y.

Отношение, характеризующее группы отметок от объектов в рамках подхода формализации нечеткости, базирующегося на обобщении понятия элемента подмножеству группы объектов, можно представить в виде нечеткого отношения сходства

R = { ^{( x}, У ) / ( x , У ) ^е X х X, ц ( x , у ) = [ 0,1 ] } , x = x ^{( v} n , t n , P n X У = У ^{( v} n , t n , P n X x , У ^e X, где n = [1, N ] – номер объекта.

В соответствии с требованиями потребите -лей представление определенной группы отметок от объектов должно осуществляться в виде конечного счетного множества. Поэтому удобно воспользоваться понятием множества уровня на нечетком отношении принадлежности (второй подход к формализации нечеткости):

Яр ={(x,У)/(x,У)е XхX,Ц(x,у)>3}, в = [0,1], где в — уровень значимости множества Кр на нечетком отношении сходства группы отметок.

Допустим, что агрегирование данных проведено без потерь. В сложной иерархической информационной системе осуществляется обработка этих данных на каждом из уровней иерархии. В ходе обработки возникают ошибки и в результате соответствующие потери информации. Определим требования к методу агрегирования с точки зрения минимизации потерь информации в системе при преобразовании и обработке агрегированных данных, т.е. требования к методу, обеспечивающему минимизацию мощности множества ошибок О , возникающих при обработке агрегированной информации.

В общем случае обработка информации в системе состоит в объединении данных, поступающих в различные моменты времени. Пусть в m [ и m [ + 1 моменты в систему обработки поступает информация о j -м агрегированном групповом объекте, которая представлена в виде пространственно протяженных объектов и описывается подмножествами X Rj^ _m 1 и X RA _{jm j+j} (рис. 1).

В результате обработки формируется объединенная информация о j-м пространственно протяженном групповом воздушно-космическом объекте XRAj :

X R-Aj = U { ^X RAjm } = { X ^{RAjm 1} Q X RAjm 1 + 1 } U j , m

U { X RAjm 1 Q X RAjm 1 + 1 } U { ^X RAjm 1 Q X RAjm 1 + 1 } '

Из выражения видно, что подмножество ошибки, возникающей при объединении информации о k -м агрегированном воздушно-космическом объекте, поступающей в различные моменты времени, является подмножеством пересечения

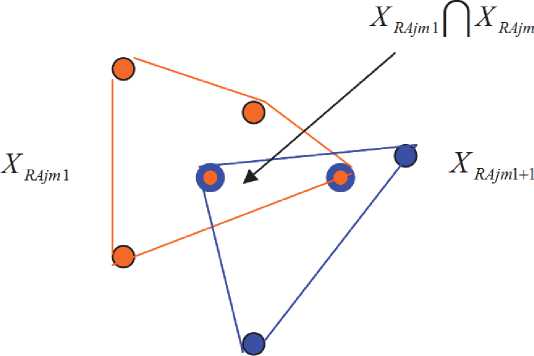
Рис. 1

мн о жеств агрегированных данных о воздушнокосмических объектах:

O j ^C { X RAjm1 A X RAjm1 + 1 } = A X RAjm ,

m m = [ m1, m1 +1].

Пусть в систему обрабо тк и на m -м периоде обработки поступают агрегированные данные по j -му групповому объекту. Для всех М j сообщений о j -м объекте на m -м периоде обработки

om с A Х RAjm^ m1 = [0, M1].

M ₁

Очевидно, ч то когда п ер есечение множеств является пустым – ошибка минимальна, т. е.

M X RAm i = O m = 0 ^ cardO m = 0.

Допустим, что в разные моменты времени на m -м периоде обработки в систему обработки поступают агрегированные данные о J с N 1 воздушно-космическом объекте. Тогда

A Ю X RAkmi

J I M 1

= A A ^XR-Ajm1 "

M 1 I J ^J

Если

A A x RAjm 1 "

M 1 I J

= 0,0 = 0 ^ cardo = 0.

То есть ошибки при объединении отсутствуют, когда множество пересечения агрегированных подмножеств групп отметок является пустым.

Пусть X - универсальное множество альтернатив, т.е. универсальная совокупность всевозможных вариантов агрегирования. Нечеткой целью в X является нечеткое подмножество, которое будем обозначать X В , т.е. нечеткое подмножество близких по координатам отметок.

Опишем нечеткую цель функцией принадлежности ц Bj : X ^ [0, 1]. Ограничения определяют множество допустимых альтернатив и также описываются подмножествами множества X .

В качестве подмножеств ограничений определим подмножество ограни че ний по скорости передвижения объектов и подмножество непротиворечивых с точки зрения объединения отметок в группы признаков.

Подмножество ограничений по скорости является нечетким и описывается функцией принадлежности μ ν : X → [0, 1].

Подмножество непротиворечивых признаков является четким и описывается функцией принадлежности, принимающей только два значения: μ _p : X → 0, если признаки противоречивы, и ц p : X ^ 1, если признаки непротиворечивы с точки зрения объединения о бъ ектов в одну группу.

Множество допустимых альтернатив определяется с использованием четкого ограничения по непротиворечивости признаков и ограничения по скорости. На нем строится соответствующее отношение сходства

^R M = { ( x B , У в ^)/( x B , У в ) ^{G X} b ^{х X} b ,

Ц в ( x B , У в ) = [0,1] } .

С точки зрения объединения отметок от объектов в одну группу известную совокупность признаков можно разделить на следующие классы: – противоречивые признаки;

– непротиворечивые признаки;

– признаки, запрещающие объединение объекта в группу.

С учетом проведенной классификации выражение для расчета функции принадлежности четкого подмножества ограничений по признаковой информации выглядит следующим образом:

Ц р ^{( х} в , У в ) = min { Ц з ^{( х} в ) Ц з ⁽ У в ) Ц н ^{( х} в , У в ) } ,

Том 2

где μ _З ( х_В ), μ _З ( у_В ) – функция принадлежности четкого ограничения по признакам, запрещающим объединение данных об об ъектах х_В , у_В в группу соответственно; μ _Н ( х_В , у_В ) – функция принадлежности четкого ограничения по непротиворечивости остальных признаков.

С учетом признаковой информации подмножество допустимых альтернатив выглядит следующим образом:

Ц в ^{( х} в , У в ) = min { Ц Bk ^{( х} в , У в ), Ц Pv ^{( х} в , У в ) } .

• ⁵⁸          При этом на множестве всех отметок от воз

душно-космического объекта проведено формирование групп отметок по координатам и признаковой информации, т. е. выделены классы сходства отметок. Для окончательной классификации, т. е.

^, для выделения стабильных во времени групп отметок, необходимо учесть ограничение по скорости.

Прежде чем это осуществить, необходимо представить агрегированную информацию в виде подмножества непересекающихся классов и определить эталон для каждого. Для чего преобразуем построенное отношение сходства в нечеткое отношение строгого предпочтения и выделим на нем четко недоминируемые альтернативы:

^Ц в ^{( х} в ) = ¹ - sup [ ^Ц в ^{( у} в , ^х в ) -^Ц в ^{( х} в , ^у в ) ] • ^х в , ^у в ^{G х} в

Уточнение полученной классификации проведем с учетом нечеткого ограничения по скорости:

Ц в ( ^х в , У в ) = ^min { Ц HB ^{( х} в , У в ), Ц v ^{( х} в , У в ) } •

Таким образом, метод агрегирования информации о воздушно-космической обстановке, обеспечивающий минимизацию ее потерь в условиях информационной перегрузки, при удовлетворении требований потребителей информации к ее качеству состоит:

• –    в формировании нечеткого отношения сходства на множестве отметок трасс воздушно-космических объектов;

• –    в определении множеств нечетко определенной цели при нечетких множествах ограничений нечетких подмножеств групп;

• –    в преобразовании матрицы нечеткого отношения сходства с выделенными на нем подмножествами групп в нечеткое отношение строгого предпочтения и выделении на нем четко недоминируемых альтернатив;

• –    в уточнении сформированных групп с учетом нечеткого ограничения по скорости.

В дальнейшем в зависимости от ограничений в информационных возможностях системы (например, по производительности) и требований потребителей данные о сформированной группе объектов могут быть представлены:

– эталонами – наиболее связанными в пространстве параметров и признаков объектами с остальными составляющими группу и косвенно характеризующими боевой порядок и обобщенными данными об остальных составляющих группу;

– эталонами и данными о составляющих группу в относительной системе координат группы с началом отсчета, совмещенным с координатами эталона без изменения масштаба относительной системы координат или с измененным масштабом.

Одним из основных требований к алгоритму с точки зрения реализации является требование, связанное с минимизацией потребных для реализации алгоритма вычислительных ресурсов и функционирования в реальном масштабе времени, что позволяет минимизировать задержки информации при обработке и соответственно ее потери за счет ухудшения качества.

Проведенные предварительные оценки показали, что алгоритм, полностью реализующий разработанный метод, может потребовать вычислительный комплекс с быстродействием, превышающим 10 млрд операций в секунду. Средний современный процессор имеет производительность на уровне 1–3 млрд операций в секунду, поэтому очевидна проблематичность реализации полного алгоритма. В связи с этим при разработке алгоритма потребуется рационализация, «усечение», упрощение метода, что является оправданным, особенно если алгоритм должен обеспечить снижение влияния неопределенности в условиях перегрузки системы.

Упрощение метода осуществлялось путем замены ресурсоемкой операции транзитивного замыкания на совокупность близких по результату операций, обеспечивающих хорошую сходимость и приемлемую точность, но являющейся значительно более экономичной [7, 8].

Проведенные оценки показали, что реализация подобных операций потребует значительно меньше ресурсов по сравнению с существующими в системе классическими алгоритмами и на несколько порядков меньше, чем операция транзитивного замыкания.

Результаты оценки качества функционирования разработанного усеченного алгоритма приведены на рис. 2. В ходе математического эксперимента оценивались информационные потери а и агрегированность (сжатость) информации. Агрегированность информации оценивалась двумя показателями – вероятностью (или частостью) правильного агрегирования Р _пр и коэффициентом сжатия информации K _сж.

Результаты оценки разработанного алгоритма показывают, что [9, 10]:

– алгоритм обладает высокой устойчивостью к влиянию ошибок оценки координат объектов

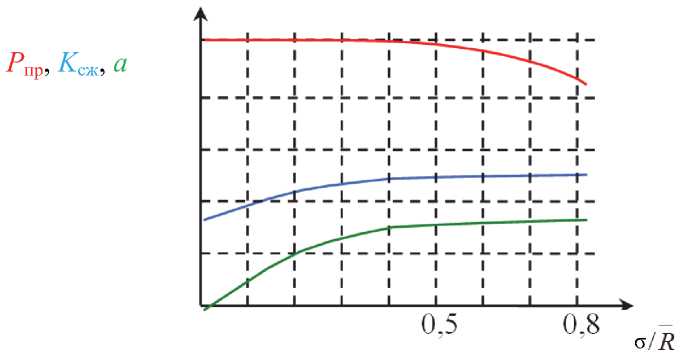
Рис. 2. Результаты работы усечённого алгоритма

и наличию ложной информации. Качество его функционирования снижается, когда ошибки становятся соизмеримыми с расстояниями между группами объектов. Ложная информация при обработке не возникает из-за формирования не-пересекающихся групп, а возникшая до агрегирования не участвует в формировании траекторий движения объектов, а влияет только на обобщенные характеристики агрегированных объектов, не расходуя вычислительные ресурсы; алгоритм обеспечивает достаточно высокую вероятность правильного агрегирования и сжатие информации в количество раз, соответству-

ющее соотношению числа неагрегированных и агрегированных объектов.

Таким образом, предлагаемый подход и разработанный метод позволяют обеспечить обработку данных о воздушно-космических групповых объектах в информационной системе с ограниченными ресурсами. Разработанный на основе предложенного метода усеченный алгоритм агрегирования обеспечивает достаточное качество агрегирования в широком диапазоне изменения ошибок оценки координат воздушно-космических объектов и повышает возможности системы в условиях информационной перегрузки в несколько раз.