Подход к построению формализованного описания информационных систем для образования и обучения

В результате прогресса информационных и когнитивных наук, искусственного интеллекта, дидактических теорий, компьютерной лингвистики, интерактивного мультимедиа и других отраслей знания, в частности, благодаря успехам международных    групп    по    стандартизации    учебно-ориентированных информационных технологий, в конце ХХ столетия возникло и быстрыми темпами развивается новое поколение информационных систем для образования и обучения (далее - ИСО2) [1–4]. При этом техническим базисом ИСО2 считается применение многоразово используемых интероперабельных объектов учебно-ориентированного контента в форме "учебных объектов (learning objects, LO)", которые используются совместно, и сдвиг потока управления от «встроенного» в учебные ресурсы к его внешнему представлению, который обрабатывается при помощи разнообразных систем ИСО2. Динамическое агрегирование LO с интероперабельными наборами метаданных позволяет приспосабливать их к потребностям, требованиям, целям и задачам каждого пользователя.

Применение  ИСО2  направлено на поддержку трансформаций и усовершенствование традиционной парадигмы обучения, перевооружение всех участников обучения, образования и тренировки, улучшение и обогащение их компетенций, значительное повышение уровня качества удовлетворение учебных потребностей, требований и спроса каждого индивидуума, группы, организации, сообщества. В настоящее время наблюдается широкое разнообразие классов ИСО2 (от простых систем доставки учебных объектов до национальных учебных систем и сетей, глобальных управляемых учебных сред, инфраструктур, киберпространств, так называемой, экономики учебных объектов). Анализ показывает, что ИСО2 и их композиты определяются и создаются с многочисленными целями и перспективами, на различных уровнях, с использованием разнообразных идей, понятий, языков, моделей, методов, правил и теорий [1–4]. Однако описания ИСО2, в подавляющем большинстве, представлены на естественных языках, не систематизированы, не унифицированы, взаимно не согласованы и т.д.. Таким образом, актуальной общей задачей является разработка подходов к построению формализованного описания ИСО2. Далее в статье представлен один из таких подходов.

Постановка задачи

Ускорение процесса интеграции Украины в мировое информационное пространство [3] и поддержка опережающего развития национального учебноориентированного киберпространства требуют разработки и широкого использования инновационных ИСО² , благодаря которым, опираясь на фундаментальные научные результаты можно преодолевать цифровое неравенство. Несмотря на значительные достижения мировой и украинской науки в сфере построения новых ИСО² , комплекс важных вопросов в этой сфере до сих пор остается проблематичным. Среди них можно выделить такие как постановка общих задач, построение общих вербальных и формализованных описаний, концептуальная неопределенность объектов учебно-ориентированного контента в форме учебного объекта (learning object, LO), построение моделей и методов агрегирования (и декомпозиции) динамических учебных объектов [5], интеллектуализация инструментария ИСО² , их адаптация к естественно-языковой среде и др. Эти вопросы усложняются тем, что их раздельное, локальное решение на каждом шагу порождает новые и новые сложные проблемы. Таким образом, возникает необходимость в исследовании и эффективной поддержке построения динамического наукоемкого объекта S [2], который является обобщенным представлением совокупности технологически возможных систем ИСО² (таких, как LMS, CMS, LCMS, NLN, LON и др. [3]) и базируется на создании и многоразовом использовании нового знания. Актуальным направлением этих исследований является решение S-проблемы - «Как лучше определять и поддерживать S?».

Анализ определений классов S и их существенных свойств (характеристик) свидетельствует о многочисленных трудностях, связанных с решением общей задачи идентификации и описания системных композитов S и их характеристик в [2]. Примеры трудностей: неопределенность единого родового понятия; использование в определениях понятий разнообразных и многочисленных существенных характеристик (ключевых понятий); отсутствие соответствующих формальных описаний. Отметим также, что постановка и решение частных, локальных задач идентификации и описания S: обычно порождает все новые и новые трудности. Кроме того, S имеет практически неограниченный набор свойств, каждое из которых можно исследовать, изучать, использовать, осознавать и оценивать по определенному конечному набору свойств. Ясно, что невозможно изучить полностью все свойства S (что следует из первой теоремы Геделя) и реальной целью исследования S является выделение и изучение только тех его свойств, которые связаны с заданной целью или проблемой.

В соответствии с базисными подходами к построению ИСО2 (LTSA, SCORM, IMS, ОКІ [2] и др., в общей схеме их построения комбинируются следующие шаги: <разработка вербального описания постановок задач> → <разработка принципиального решения задач > → <разработка вербального описания модели агрегирования контента (SCORM)> → <разработка частичных решений на базе XML/RDF-формализмов> → <практическая реализация решений> [2]. Ключевым аргументом в пользу применения формальных конструкций и структур XML/RDF в данной схеме является тот факт, что Веб (Семантический Веб) стал, де-факто, стандартной общей платформой для ИСО2. На наш взгляд, такой традиционный подход существенно ограничивает потенциал применения формализованных описаний ИСО2, особенно на этапах исследования и общего (не детализированного) проектирования ИСО2 и их композитов, т.е. „с самого начала”.

Одним из общих подходов к описанию различных классов систем и их свойств является язык теории категорий [6-7]. Таким образом, актуальной общей задачей является разработка подходов к построению формализованных описаний ИСО² с использованием теории категорий, а также их содержательные интерпретации.

Подход

В монографии М. Месаровича [6] определенные математические конструкции теории категорий используются для описания различных классов систем и взаимосвязей между ними. В частности, в качестве объектов категории берутся просто системы, т.е. отношения на определенных множествах, а морфизмы (как функции, определенные на соответствующих множествах) вводятся и рассматриваются различными способами.

В предлагаемом подходе к построению формализованного описания ИСО² эти конструкции не рассматриваются, применяется аксиоматический метод формализации и в явном виде вводятся правила вывода и логика. Во второй половине ХХ века была установлена связь между формальными аксиоматическими теориями (или дедуктивными системами, исчислениями) и категориями. А именно, исчисление или дедуктивную систему можно преобразовать в категорию, морфизмы которой определяются выводами в исчислении. Ловер предложил рассматривать формальные теории как категории, морфизмы которых определяются термами и формулами, а композиции морфизмов задаются при помощи операции подстановки терма вместо свободных переменных [8]. Взгляд Ловера на теорию как на определенный тип категории расширяет возможности метода моделирования, дает единый взгляд на понятие модели. Отметим, что имеется определенный выбор подходов для аксиоматизации минимальной формализованной структуры и конструкции (далее -м.ф.с.) „категория”. В частности, в работе Хетчера [9] предложено простой подход, суть которого состоит в замене объектов категории единичными стрелками, т.е. все индивиды (предикатные буквы) являются стрелками (в отличие от подходов, в которых вводится два сорта переменных: один - для объектов, а другой - для стрелок категории).

Обозначим l,lax>- класс абстрактных систем S^l,lax (т.е. класс ИСО² ) с уровнем абстракции I, который определяется lax аксиомами. Каждый класс абстрактных систем S^Uax определяется аксиоматическим методом путем добавления к м.ф.с. категория новых аксиом. Добавление новых аксиом может вызвать изменение м.ф.с. и тогда уровень абстракции S^l,lax уменьшается, а значение l -наоборот увеличивается, т.е. I. = I. + 1 или в общем случае до I', где I. < I'.

Примеры определения значений l, lax:

• S¹¹    -это S с l =1 - наивысшим уровнем абстракции и с числом аксиом tax = 1*, где 1* +1 = 2, 1* +2 = 3 и т. д., т.е. для удобства считаем, что «стартовое» число аксиом равно 1.

• S²²    - это S с уровнем абстракции 2, что означает использование следующей м.ф.с., а lax =2 - означает, что к набору аксиом, при помощи которых задают эту следующую м.ф.с. добавляется еще одну аксиому (или один набор аксиом).

Тогда общая постановка задачи построения формализованного описания

ИСО² на базе м.ф.с. категория записываются в виде:

_Dp s . < < ^ - -ax . ^ <§¹ ', ^1ах ' >>

где:     DP - определенный процесс;

• <> - обозначение комбинации того, что содержат эти скобки.

Примеры свойств (характеристик) Ŝ^ℓ,ℓax :

U(S) - суперкласс элементарных информационно-дидактических единиц (ЭИДЕ) [2] на S . Классы U(S) или их члены обозначаются как u(S) или просто и;

MOD, MOD i , mod i - суперклассы, классы или члены классов (частичные модели) общей модели контента (далее - ОМК);

f g, h - этими латинскими буквами обычно обозначают композиты DP^S, которые обычно называются §^1,1ах-стрелками, а композиты типа U(S), MOD - обычно называются S^ ax -объектами и обозначаются латинскими буквами a, b, c, d.

Описание отображений l,lax> ^ l ,lax > осуществляется с сохранением категорной структуры. Поэтому необходимо введение и применение понятия функтор . Введение функторов (как стрелок) между категориями означат „поднятие” на новый уровень абстракции. С технических соображений, чтобы не перегружать описание решения задач (1), в описаниях DP и др. этот показатель не отображается. Поскольку в этих описаниях необходимо «поднятие» еще на один уровень абстракции - рассматривать функторы как объекты. С другой стороны, также требуется определять подсистемы S^ax (как подкатегории), а также взаимодействие между ними на одном или более уровней абстракции.

Уточнение постановки задачи (1) и ее решение с содержательными интерпретациями вплоть до введения логики предикатов являются ключевыми направлениям построения базисного формального описания S^l,lax с использованием м.ф.с. теории категорий.

Отметим, что двумя общими стратегиями построения формализованного описания являются:

• 1)    введение дополнительной структуры для базисных конструкций S^l,lax. Например, определенный объект интерпретируется как некоторое множество с подходящей структурой ;

• 2)    введение структуры непосредственно для самих объектов S^l,lax.

Первым шагом решения задачи (1) является определение и содержательная интерпретация родового понятия «абстрактная система Ŝ¹¹ » на базе м.ф.с. категория [5] (которую назовем слабо структурированная S) .

Определение. Слабо структурированная S по определению содержит:

• 1)    совокупность ресурсов, которые называются S -объектами ;

• 2)    совокупность ресурсов, которые называются S -стрелками ;

• 3)    операции (ресурсы), которые ставят в соответствие каждой S-стрелке f S-объект input f (начало стрелки, входной элемент) и S-объект output f (конец стрелки, выходной элемент / в том числе цель). Если a = input f, а b = output f , то эквивалентной является запись:

J: а -* Ь, або а —* Ь;

• 4)    операцию, которая ставит в соответствие каждой паре ( g, f) S -стрелок с input g = output f S-стрелку gf (или тождественную запись g°f) , композицию f и g , с input (gf) = input f и output (g°f) = output g , т.е., g°f : input f ^ output g , причем для каждых следующих §¹¹-объектов и §^п-стрелок

/ g А а —*Ь —»с —»d, справедлива аксиома ассоциативности: h°(g°f) = (h°g)°f.

• 5)    аксиома тождества . Для любых S-стрелок f: a ^ b и g: b ^ c справедливо I_b°f = f i g° I b = g, де I b - единичная стрелка (для каждого S-объекта b и S-стрелки I_b справедливо I_b : b ^ b).

Рассмотрим пример содержательной интерпретации компонентов Ŝ. Обозначим М – компоненты учебных материалов дистанционного курса, темы, урока и т.д. Тогда в М должны быть:

Содержание М – это MC(U(S)) – понятия, принципы и т.д. предметной области (ПрО), где U(S) – класс ЭИДЕ, которые обычно представлены в ОМК [2];

Форма представления М – это MF. Например, в онтологиях дидактического контекста необходимо специфицировать контекстные ЭИДЕ: вступление, анализ темы и т.п., дискуссия по теме, контексты презентации (пример, иллюстрация) ;

Структурные отношения H между MF, MC. В структурных онтологиях специфицируют «грамматические» правила комбинирования персонализированных единиц, композитов. Примеры ЭИДЕ: следующий, предыдущий, отношения ispartof, haspart, isversionof, hasversion, isformatof, hasformat, references, isreferencedby, isbasedon, isbasisfor, requires, isrequiredby ispartof, isbasedon из LOM [2].

Компоненты в определении Ŝ интерпретируются следующим образом: M = a, MF = b, MC = c , f: M → MF, g: MF → MC, g°f : M → MC. Другими словами, в данном случае описана содержательная интерпретация определения Ŝ на базе универсального отношения «форма-содержание».

Важно отметить, что имеются и другие содержательные интерпретации определения Ŝ, например, на базе диаграммы (частичной модели декомпозиции-агрегирования контента) <<Агрегатор>, <Генератор>, <Анализатор>> [2]. Эти интерпретации относятся к высшему уровню абстракции и могут рассматриваться как подклассы класса S¹¹ (или как подкатегории категории S¹¹ ).

Много композитов ОМК, которые поддерживаются на S, уже идентифицировано и описано, в частности, на базе соответствующих дидактических теорий, но в целом класс U(S) пока еще остается „недоступной системой» ЭИДЕ”. Итак, необходимо формально определить в ОМК итоговый конечный набор комбинаций [представленных в MOD, ..., i > ] из которого при помощи итогового конечного набора дидактически обоснованных правил можно получать любые персонализированные учебные материалы . Использование последних дает возможность удовлетворять потребности или достигать измеряемые учебные цели каждого обучаемого. Тогда в категорных терминах данная задача формулируется следующим образом: «Необходимо формально описать: „Как лучше определить и MOD как начальный и итоговый Ŝ^ℓ,ℓax- объекты ?” – или наоборот – Необходимо определить как итоговый Ŝ^ℓ,ℓax- объект , а MOD -как начальный Ŝ^ℓ,ℓax- объект (что одно и тоже по принципу двойственности [9])».

Еще в 1969 году Р. Джерард сформулировал концептуальную идею (КИ) учебных объектов для образования и обучения при поддержке информационных технологий – „Учебные единицы нужно производить более малыми и комбинировать их в огромное разнообразие специфических учебных программ, приспособленных к каждому обучаемому подобно тому, как комбинируются компоненты конструкций в стандартизированных конструкторских наборах” [10].

Вербальное описание КИ-Джерарда : „ Учебные единицы нужно производить более малыми [M(U(S), цель МAG(M(U(S)))] и комбинировать их [=<МA(M(U(S))), МG(M(U(S))), МAG(M(U(S)))>] в огромное разнообразие специфических учебных программ [=M(U(S)], приспособленных [= цель МAG (U(S)] к каждому обучаемому [=Γ]”.

Формальное описание КИ-Джерарда с использованием класса частичных моделей ОМК <<Агрегатор> [=МAG(M(U(S)))], <Генератор> [=МG(M(U(S)))], <Анализатор> [=МA(M(U(S)))]>, и следующего декартового квадрата:

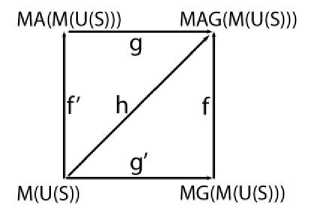
Пример дидактической интерпретации компонентов этой диаграммы Γ, U(S), M(U(S), . Авторы известных дидактических теорий Reigeluth, C. M. & Nelson, L. M. Описывают и рассматривают типичный учебный контекст (ситуацию) [11]: "Когда преподаватели [=Г] впервые получают учебные материалы [=], то они часто разбивают их на составляющие части [= / ] и в дальнейшем составляют различными способами [=<, >], чтобы поддерживать свои индивидуальные учебные цели [=]. Отмеченный контекст подсказывает одну из причин того, что именно ориентация на многоразовое использование учебных компонентов может быть выгодной и полезной с дидактической точки зрения ” ([=...] - наше).

Отметим также, что компоненты <<Агрегатор>, <Генератор>, <Анализатор>> в определении Ŝ интерпретируются следующим образом: MAG = c, MA = a, MG = b , f: MA ^ MG, g: MG ^MAG, g°f : MA ^ MAG.

Рассмотрим ряд базисных определений концептов и свойств абстрактной S ( S¹¹ ).

Определение: относительная §. Относительные § (обозначаются как S|a, Sfa) - это специализации S стрелок, при которых их рассмотрение ограничивается только стрелками с фиксированным концом (далее - output ) или началом (далее - input ). Формальное описание: обозначим a - любой объект S. Тогда объектами S|a объектов над а являются все стрелки S с концом в объекте a , и стрелками из f: b ^ a в g: b ^ c - это такие S-стрелки k: c ^ a , что диаграмма

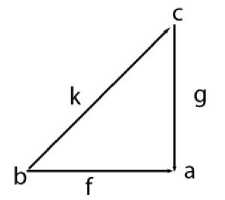
является коммутативной, т.е. g°k = f.

Относительная Sfa определяется аналогично S|a с использованием принципа двоичности (со следующей заменой в формулировках: Sfa объектов под а вместо S|a объектов над a) . Композиты (S|a, Sfa) играют важную роль для построения формального описания S. Например, при помощи данных композитов описываются и рассматриваются целевые а.

Определение : подсистема S. Обозначим:

• a, b - объекты S,

Ŝ(a, b) - совокупность S-стрелок с input а и output b ,

S(a, b) = {f: f является S-стрелкой вида f: a ^ ^{b }}

Тогда S называется подсистемой В (обозначение: S с В), если:

• (1)    каждый S-объект является В-объектом и

• (2)    для любых a, b S-объектов справедливо S(a, b) = B(a, b), т.е. В не имеет стрелок a ^ b, которые не принадлежат S.

Определение: функтор. F: l,lax> ^ l ,lax > называется функтором , если:

• (1)    каждому <§^1,1ах>-объекту а соответствует l ,lax >-объект F(a) ;

• (2)    каждой <§^1,1ах>-стрелке f: a ^ b соответствует^^{1 ,lax} >-стрелка

F(f): F(a) ^ F(b) ,

(2a) F(1_a) = 1_F ( _a ) для каждого <§^1,1ах>-объекта a ;

• (2б)    F(g°f) = F(g)°F(f) для любых f и g, для которых определена композиция g°f.

Определение: mod-диаграмма в S. Композит mod-диаграмма в § - это совокупность объектов modi, mod j , совместно с S-стрелками g: mod i ^ mod j между объектами с этой диаграммы. Обратите внимание, что количество стрелок между объектами не обязательно является определенным.

Пример содержательной интерпретации понятия mod-диаграмма в S . Обозначим modi и mod j -члены наборов частичных моделей общей модели контента (ОМК), которую реализует S . Тогда новый „потенциальный” член набора (или некоторое инновационное агрегирование контента - ИАК) вначале идентифицируется и по принципу частичного понимания [13] относится к классу частичных моделей более высокого уровня. В дальнейшем он шаг за шагом уточняется или вообще отбрасывается как известный объект (это означает, что стрелок mod i ^ mod j вообще нет). Для формального описания подобных взаимосвязей и трансформаций и используется композит mod-диаграмма в S.

Определение: Конструктив для mod-диаграммы в S - это такой S-объект и вместе с S-стрелками f: u ^ mod_t для каждого объект mod i с mod-диаграммы в S, что следующая диаграмма

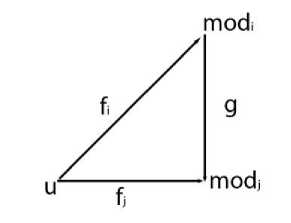
является коммутативной для любой стрелки g из mod-диаграммы, т.е. gfi = fj .

Пример интерпретации понятия . В приведенной диаграмме объект и интерпретируется как член , а mod_t и mod j - это члены наборов частичных моделей ОМК, которые нужно определить полностью.

Определение: -диаграмма. Границей mod-диаграммы называется -диаграмма { f: и ^ mod i } такая, что для любой другой - диаграммы { fi: u’ ^ mod i } существует только одна стрелка f: и’ ^ и, для которой диаграмма:

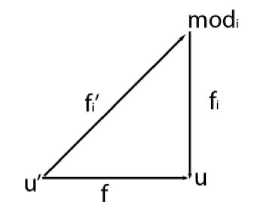
коммутативна на каждом объекте mod i из mod -диаграммы.

-диаграмма универсальна относительно всех своих -диаграмма является универсальным свойством (характеристикой) – для всех -диаграмма.

Пример интерпретации понятия -диаграмма . В приведенной диаграмме объект u интерпретируется как идентифицированный член для класса mod i частичных моделей ОМК и любой другой u´ из для этого класса является эквивалентным (как всегда с точностью до изоморфизма). Или другими словами, класс ( mod i ) частичных моделей ОМК определено полностью относительно .

Определение: конечная полная S. Система § является конечно полной, если она содержит границу любой своей конечной диаграммы. Конечная диаграмма содержит конечное число объектов и стрелок между ними.

Определение: произведение двух объектов в S. Произведением двух объектов a и b в § называется S-объект a х b вместе с парой (pr a : a х b^a, pr b : a х b^b ) S-стрелок, такой, что для любой пары (f: c ^ a, g: c^b ) существует одна и только одна стрелка : c ^ a х b , для которой диаграмма:

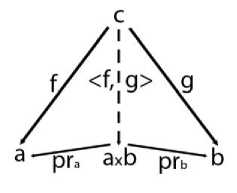
коммутативна, т.е. pr_a ° = f и pr_b ° = g . Стрелка называется произведением стрелок f и g относительно проекций pr_a, pr_и . ( произведение двух объектов в Ŝ определено с точностью до изоморфизма).

Пример содержательной интерпретации понятия произведение двух объектов в Ŝ . Обозначим <Ќ> = <i>,… i>> – совокупность комбинаций компетенций. Каждую компетенцию K i представлено в виде набора значений k i1 , k i2 , …, max k i >, которые формируют Ќ i -пространство значений этой компетенции. Тогда частичным пониманием К является декартовое произведение этих K i [14]:

<К>    = K1 х K х Кз ... х Kmax

Каждое значение k_i (как результат достижения измеряемой учебной цели с описанием <ОМК_учебная-цель>) можно формально определить при помощи класса MOD-компетенции ОМК (примеры членов этого класса: <ОМК_понятие>, <ОМК_принцип>, … <ОМК_тест>) и класса MOD-агрегации. А это означает, что необходимо иметь возможность определять, в частности, композиты вида K i х K j ^ MODi (и вообще вида MODi х MODj х ...). Таким образом, введение этого понятия и конструкта моделирования дает возможность, в частности, формально определять комбинации MODi при помощи Ŝ (на базе релевантных дидактических теорий).

Определение . Ŝ допускает экспонирование, если в ней существует произведение любых двух объектов и если для любых двух объектов a и b существует Ŝ-объект b^a , который называется э кспоненциалом , и Ŝ-стрелка ex: b^a×a →b , которая называется стрелкой значения , такие, что для любых Ŝ-объекта c та Ŝ –стрелки g: c×a → b существует единственная Ŝ-стрелка ĝ: a → b^a для которой диаграмма:

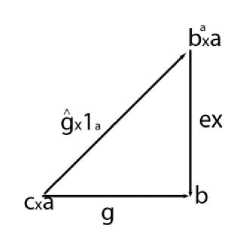
является коммутативной - ex ° (g 1a) = g, где x - это декартовое произведение .

Замкнутая Ŝ – это конечная полная Ŝ, которая допускает экспонирование.

Определение . S¹² - это (декартово) замкнутая S¹¹ ;

Пример интерпретации. (=a) является „относительно устойчивой системой с конечным набором ЭИЕ, ЭИДЕ”. Если имеет m ЭИДЕ, а n ОЧМ, то <^U(S)>имеет nm элементов. Итак, суть определения S¹² при помощи указанной диаграммы состоит в том, чтобы в терминах стрелок охарактеризовать все DP с inputs с и outputs (значениями) в ex (правило).

Следующим шагом построения формализованного описания § является построение описания Ŝ²¹ . Для этого необходимо использовать следующие определения: „под-объект § (категорный аналог понятия подмножество); классификатор под-объектов S\

Определение: под-объект § . Под-объектом § -объекта d (или под-объектом в d ) называется моно-стрелка f: a >^ d с концом в d .

Определение: классификатор подобъектов S. Обозначим знаком 1 конечный объект § . Классификатором подобъектов S называется S-объект 6 вместе с S-стрелкой true: 1^ 6 , такой что справедлива следующая 6 -аксиома.

Определение: 6 -аксиома. Для каждой моно-стрелки f: a >^ d существует только одна S-стрелка X f : d ^ 6 , для которой следующая диаграмма

а >---------d

i                            X,

true

Является декартовым квадратом; ^ - это единственная стрелка, а стрелка %f называется характеристической стрелкой (аналог характеристической функции на множестве) моно-стрелки f Если классификатор подобъектов существует, то он является единственным с точностью до изоморфизма .

Определение: S21 - это S12 , имеющая классификатор под-объектов ( 6 -аксиома).

Определение: S22 - это S21, что для каждого S21-объекта d-решетка является булевой алгеброй. Для определения S22 используется: - аксиоматическая система (классическая логика CL имеет единственного правило вывода); - 6 -аксиома; - понятия d- решетка (аналог частично упорядоченного множества с inf и sup [15], но для стрелок f и g ). Таким образом, в § типа S22 формально введено правила вывода. Дальнейшее построение аксиоматического описания S осуществляется на базе соответствующих теорий логики.

Заключение

Актуальными направлениями применения предложенного подхода являются:

• -    идентификация и систематизация разнообразных содержательных интерпретаций композитов Ŝ и релевантных формализованных конструкций;

• -    прогнозирование новых свойств композитов Ŝ на базе имеющихся и новых формализованных описаний (теорем, утверждений, процедур);

• -    разработка постановок новых задач и их решение, интерпретация на Ŝ;

• -    построение аксиоматических описаний S на базе подходящих теорий логики, а также их содержательные интерпретации;

• -    построение формализованных описаний учебно-ориентированных электронных пространств.

Предложенный подход принципиально расширяет возможности традиционного инструментария по идентификации, описанию и прогнозированию свойств информационных систем для образования и обучения, предоставляет новые возможности для обмена результатами, устраняет неопределенность описаний этих систем «с самого начала». На наш взгляд, решающим фактором для формализации свойств Ŝ является не обеспечение „правильности” определения м.ф.с. для каждой его содержательной интерпретации, а то, насколько ее можно ясно и однозначно понять и в последующем исследовать и использовать, в частности, в других дисциплинах и подходах.