Подходы к Физико-химическому моделированию скоростей изменения дефектов в полидиметилсилоксановых материалах

Большинство конструкционных и функциональных материалов со временем теряют свои свойства и разрушаются, что неизбежно сказывается на надежности приборов и конструкций, выполненных из таких материалов. Поэтому в последнее время все больший интерес привлекают самозалечивающиеся материалы, способные восстанавливать свою структуру после воздействия [1–3]. Существуют различные механизмы восстановления свойств полимерных материалов. Химические процессы, отвечающие за восстановление структурных особенностей [4] основаны на обратимых химических реакциях, таких как диссоциация/ассоциация, присоедине-ние/элиминирование, реакции Дильса – Альдера, координационные взаимодействия металл – лиганд и т. д. Физические процессы, такие как текучесть и диффузия растворенных газов, также оказывают влияние на динамику и обратимость процессов восстановления или изменения свойств [5].

Дефекты в материалах, обладающих большой электрической прочностью, имеют свою специфику и требуют отдельного исследования [6]. Повреждения в изоляционных материалах, приводящие к потере электрической прочности, накапливаются годами [7]. Вероятность развития электрического пробоя определяется размерами образовавшегося дефекта и величиной напряженности электрического поля в материале.

Большинство изоляционных материалов безвозвратно утрачивают изоляционные способности после пробоя [7]. Поэтому дальнейшие исследования новых изоляционных материалов с воз- можностью восстановления свойств остается актуальным. Неоднородности в изоляции кабельной продукции могут приводить к развитию проводящих древовидных каналов, известных под названием триингов. Они бывают двух типов: электрического происхождения и так называемые водные триинги электрохимического происхождения. Согласно [5, 8], одними из весьма перспективных самовосстанавливающихся изоляционных материалов являются силиконовые гели. В работе [5] продемонстрировано существование процесса самовосстановления в подобных гелях как во время развития канала триинга под воздействием электрического поля, так и после снятия напряжения. Основными механизмами восстановления в этой работе названо растворение газа, образовавшегося в канале триинга, в веществе вокруг канала и уменьшение объема канала благодаря вязко-упругим свойствам геля.

Также перспективными самовосстанавливающимися материалами являются полидиметилси-локсаны (ПДМС), поскольку эти материалы обладают высокой электрической прочностью. В работе [9] исследован электрический пробой в полисилоксанах и показано частичное восстановление свойств образца после электрического пробоя. При электрическом пробое выделяется большое количество энергии, которая приводит к нагреванию образца и необратимым химическим реакциям. Поэтому более интересным является развитие дефектов на стадии, предшествующей полному электрическому пробою [10–11], когда энергии не столь велики чтобы вызвать необратимые процессы (скорость возрастания мощности не более 2 кВт/с, соответствующая частичным разрядам [12]).

При исследовании ПДМС можно выделить два аспекта: во-первых, это восстановление на физическом уровне свойств образца в приграничной области дефекта и однородности материала в целом; во-вторых, это восстановление химической структуры сополимерной цепи [13], в том числе, за счет поперечных сшивок, формируемых сополимерными фрагментами. При восстановлении физико-химических свойств важную роль оказывают процессы перемещения массы вещества или диффузия за счет сил поверхностного натяжения и т. д.

О восстановлении структуры полимерного материла можно косвенно судить по восстановлению физико-химических свойств образца [13]. Характеристики эффективности и скорости процессов самовосстановления могут оцениваться по изменению размеров дефекта. Для дефектов различной природы сравнение скоростей самовосстановления может свидетельствовать о значимости тех или иных факторов, влияющих на возникновение дефектов.

Для выявления влияния электрического пробоя на изменение свойств образцов на основе ПДМС предложен новый подход, основанный на сравнении поведения образца при механическом способе образования дефектов и при образовании дефектов в результате электрического пробоя малой мощности. При моделировании процессов учитывалось растворение газов в образце и воздействие на границу дефекта сил поверхностного натяжения.

В нашей работе были поставлены следующие задачи: во-первых, разработка физикохимической модели самовосстановления полимерного материала после возникновения дефектов в виде пузырьков; во-вторых, разработка эффективного метода, позволяющего проводить сравнительный анализ самовосстановления прозрачных аморфных материалов путем сравнения скоростей для случаев самовосстановления материала после механического и электрического пробоя.

Обсуждение результатов

Исследование было проведено для образцов ПДМС, реологические характеристики которых были близки к аморфным гелеобразным полисилоксановым материалам. Материал может быть охарактеризован, как обладающий довольно высокой прозрачностью, позволяющей наблюдать за формированием, движением и растворением пузырьков в его объеме.

Литературные данные [12] указывают на хорошую растворимость газов в силиконовой жидкости, достаточно близкой по химическому составу с образцами ПДМС. Как правило, движущей силой процесса является избыточное давление вблизи поверхности дефекта, образовавшееся под действием сил поверхностного натяжения. В результате происходит перенос газов из меньшего объема – дефекта в виде пузырька в объеме образца в больший объем – атмосферу. Аналогичный процесс известен в литературе под названием изотермической перегонки [14].

Модель для восстановления свойств образца после электрического пробоя. При комнатной температуре исследуемый материал обладает невысокой текучестью. Поэтому электрические дефекты, имеющие цилиндрическую форму, сохраняют свое положение в пространстве относительно электродов. Длина дефекта (высота цилиндра) существенно больше его радиуса. Это позволяет рассматривать электрические дефекты как объекты с цилиндрической симметрией. Согласно [12] в силиконовой жидкости электрический пробой малой мощности приводит к образованию в дефекте водорода и угарного газа. Ввиду схожего состава предполагаемых в дальнейшем тестировании образцов силиконовой жидкости и образцов ПДМС, можно будет считать, что в рассматриваемом случае также могут образовываться эти же газы.

Процесс перемещения газов, растворенных в возможных образцах полисилоксановых мате- риалов, описывается уравнениями диффузии [14]:

d C ( m )h d t

^D ( m )

^{( m ) h} .A d ^C ( ^{m )h}

,

d r ²      r d r

\                    7

где C(m)h – концентрации, моль/м3, растворенных в ПДМС азота (m = 1), кислорода (m = 2), во- дорода (m = 3) и угарного газа (m = 4) соответственно, D(m) – коэффициенты диффузии этих газов в жидкости, м2/с, для цилиндрической системы координат A = 1.

Для решения уравнений диффузии вида (1) для каждого из газов необходимы граничные условия для концентрации газа на границах «ПДМС-дефект» и «ПДМС-атмосфера». На границе с атмосферой r = R ( _N ) концентрация газов C ( _m )_h ( R _N ) определяются растворимостями газов (константой Генри) и атмосферным давлением.

Для получения условий на границе дефекта r = R V рассмотрим процессы в газовой и жидкой фазах. Процесс растворения M -числа газов, содержащихся в дефекте, достаточно медленный и состояние газа в дефекте можно считать квазиустановившимся. Поэтому для состояния газа в дефекте применим уравнение для идеального газа:

P = S M1 C ( m )g ^RT . (2)

где P – давление [Па], T – температура [K], R – универсальная газовая постоянная, C _{( m )g} – концентрации газов ( m = 1… M ) внутри дефекта, моль/м³.

Для каждого из газов связь между концентрацией газа C(m)g внутри дефекта и концентраци- ей этого газа в приграничном слое жидкости около дефекта C(m)h определяется растворимостью газа [15], избыточным давлением за счет поверхностного натяжения и описывается уравнением:

C ( m )h

= K ( m )

(

, RT 1 +

\

AS ^

R V P 7

( m )g .

В уравнении (3) K _{( m )} – константа Генри для газа m , моль/(л·атм), S – коэффициент поверхностного натяжения, Н·м, A = 1 для цилиндрической системы координат.

Количество газа (в молях), проходящее через границу раздела фаз в течение времени d t , определяется законом Фика [14, 15]:

d П ( m ) =— D ( m ^C ^h S ( R v )d t .                           (4)

d r

В уравнении (4) S ( R _V) = 2 n R _V L - площадь соприкосновения фаз для цилиндрической системы координат. Уравнение (4) позволяет получить разностное уравнение для изменения концентрации веществ в дефекте, которое преобразуется в дифференциальное уравнение:

R v d C ( m )g + BC ( m )g d R V = - BD ( m ) d C ^ m ^ d t .                         (5)

Параметр В = 2 для цилиндрической системы координат.

Уравнение (5) для каждой составляющей газовой смеси совместно с (2) позволяет получить разностное уравнение для изменения радиуса дефекта:

dR_N =-У M d C m h RT d t (6)

• V m=^{m = 1} d r P

Таким образом, полученная система уравнений позволяет рассчитать концентрации газов на границе дефекта C _{( m )h} ( R _V ( t )) и определить временную зависимость для границы дефекта R _V ( t ) . Основным результатом моделирования является функция R _V ( t ) , поскольку именно изменение радиуса дефекта можно фиксировать в ходе эксперимента.

Модель для восстановления структуры образца после возникновения механического дефекта . Механические дефекты имеют шарообразную форму, поэтому, пренебрегая влиянием границ на процессы восстановления, можно ограничиться условием сферической симметрии в модели, считая радиус дефекта R _V ( t ) и внешний радиус образца R _N . Исходя из способа формирования механических дефектов, в дефектах будет содержаться атмосферный воздух, который в модели заменен смесью кислорода и азота.

Для механических дефектов процессы в исследуемом материале описываются уравнениями вида (1), а условия на границе дефекта – уравнениями вида (3), (5), (6). Однако имеются некоторые отличия. Для механического дефекта ограничимся уравнениями для двух газов: азота ( m = 1) и кислорода ( m = 2). Также необходимо учесть, что механические дефекты обладают сферической симметрией. В уравнениях (1) и (3) параметр A = 2, в уравнении (5) параметр В = 2.

Выбор параметров имитационных моделей. Данные [12] о растворимости газов в силиконовой жидкости: Н 2 – 8,7 %, N 2 – 11 %, CO – 12 %, воздух – 16,5 % позволяют оценить константы Генри. Растворимости газов в образце SR и силиконовой жидкости приняты одинаковыми из-за их близкой химической структуры и отсутствия экспериментальных данных по образцу.

Для моделирования при нормальном атмосферном давлении использованы следующие концентрации газов: C (1) p = 3,8 моль/м ³ , C (₂) _p = 3,18 моль/м ³ , C (₃) _p = 3,49 моль/м ³ , C (₄) _p = 0,54 моль/м ³ . Также по аналогии между силиконовой жидкостью и образцом SR была выполнена оценка для констант Генри: K (1) = 4,9∙10^–3 моль/л∙атм, K (2) = 14,9∙10^–3 моль/л∙атм, K (3) = 3,88∙10^–3 моль/л∙атм, K (4) = 5,36∙10^–3 моль/л∙атм.

Оценка коэффициентов диффузии газов в образце силоксанового равновесия основана на данных о коэффициенте диффузии водорода в трансформаторном масле [16, 17] D = 3,5∙10^–9 м²/с. Данные о вязкости силиконовой жидкости [12] 17,8 Па∙с и образца SR 127 Па∙с позволили пересчитать коэффициенты диффузии для образца SR с учетом вязкости: D (1) = 3,8∙10^–10 м²/с, D (2) = 4,1∙10^–10 м²/с, D (3) = 4,9∙10^–10 м²/с, D (4) = 3,8∙10^–10 м²/с.

Также при моделировании использованы следующие параметры: атмосферное давление P = 101325 Па, универсальная газовая постоянная R = 8,31 Дж/моль∙К, внутренний радиус дефекта R V = 0,17 мм, внешний радиус образца R N = 1,5 мм.

Использованные для моделирования величины могут отличаться от данных для силиконовой жидкости или ПДМС. Поэтому в дальнейшем в опыте с электрическим пробоем был использован прием нормировки данных аналогично данным опыта с механическими дефектами (пузырьками), который был выполнен с тем же образцом ПДМС.

Моделирование процесса изменения дефекта шарообразной и цилиндрической формы позволило выявить некоторые закономерности. Наблюдение за изменением дефекта осуществляется по фотографии дефекта в проходящем через дефект свете. Поэтому основным наблюдаемым параметром является изменение площади проекции дефекта на плоскость. В течение небольшого промежутка времени (20–30 % от полного времени восстановления) изменение площади дефекта приблизительно можно оценивать линейной функцией:

S (t) = 1 - A D K1, (7) y ’ a D K где a0, a - коэффициенты поверхностного натяжения в базовом и рассматриваемом режиме; D0, D – коэффициенты диффузии в базовом и рассматриваемом режиме; K0, K – константы Генри в базовом и рассматриваемом режиме; A – коэффициент аппроксимации, полученный в базовом режиме.

Уравнение (7) качественно согласуется с данными работ [18, 19], в которых также отмечена линейная зависимость уменьшения скорости проекции дефекта на плоскость наблюдения. Ука- занная линейная зависимость в [18] использовалась авторами для определения коэффициента диффузии. Это уравнение показывает, что параметр σDK можно рассматривать как основную характеристику процесса восстановления дефекта в зависимости от параметров материала. Произведение коэффициента поверхностного натяжения σ, коэффициента диффузии D, и константы Генри K, показывает, что для эффективного самовосстановления материала необходимы как процессы отвода газов из дефекта, так и наличие избыточного давления в дефекте из-за сил поверхностного натяжения. Таким образом, процесс исчезновения дефекта близок к процессу изотермической перегонки [14].

Если учесть отличие параметра А для цилиндрического и сферического дефекта, то по отношению скорости восстановления дефекта при электрической и механической природе дефекта можно оценивать влияние различных факторов, влияющих на изменение дефекта после электрического пробоя.

в)

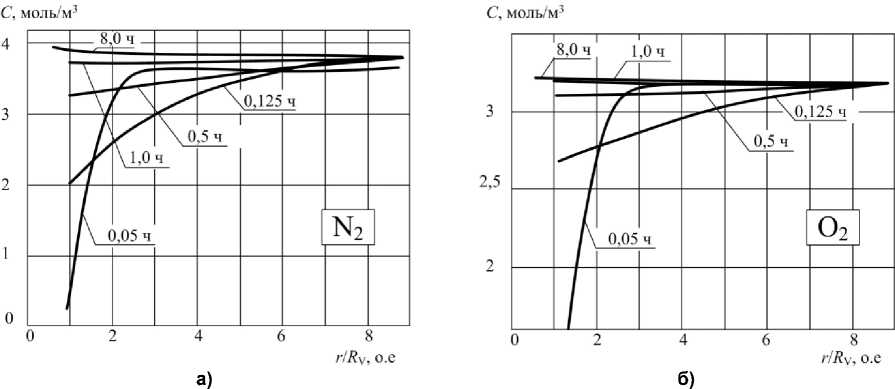
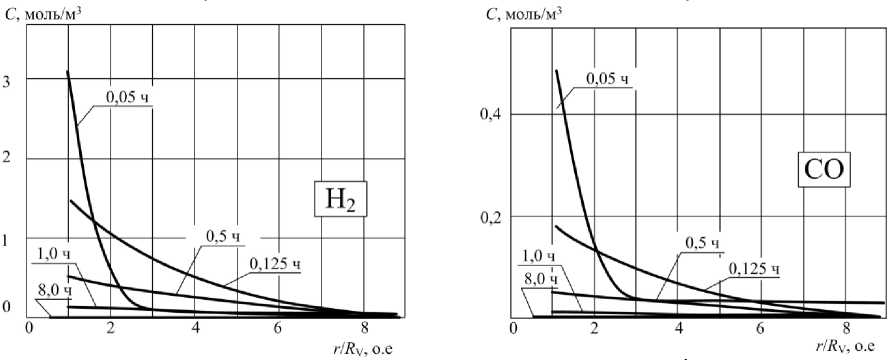
Рис. 1. Зависимость концентрации газов от радиуса дефекта для азота (а) кислорода (б), водорода (в) и угарного газа (г) в моменты времени 0,05 ч, 0,125 ч, 0,5 ч, 1,0 ч и 8,0 ч после образования дефекта

Для дефекта, созданного при пробое диэлектрика, было проведено исследование динамики изменения концентрации газов, растворенных в образце ПДМС. На рис. 1 показаны распределения концентрации растворенных газов С , моль/м³, от радиуса дефекта (нормировано на R V ). Расчеты выполнены при параметрах, аналогичных использованным ранее при моделировании динамики поведения механических пузырьков.

Анализ графиков на рис. 1 показывает, что примерно через час, образовавшиеся в дефекте водород и угарный газ замещаются азотом и кислородом, растворенным в образце полисилоксана благодаря контакту с атмосферой. Аналогичный вывод можно сделать на основании таблицы, где показано изменение концентраций газов в дефекте.

Изменение концентрации газов в дефекте, моль/м3

Время, ч	0	0,05	0,125	0,5	1,0	8,0
N 2	0	3,12	17,3	27,33	31,21	32,83
O 2	0	2,41	7,41	8,59	8,41	8,78
H 2	37,42	32,56	15,29	5,32	1,48	0
CO	4,19	3,51	1,37	0,38	0,08	0

Также при исследовании было проведено сравнение скоростей восстановления дефектов различной природы: механических дефектов и дефектов, возникших в результате электрического пробоя.

На рис. 2 показано изменение площади проекции дефекта, возникшего в результате электрического пробоя (точки – эксперимент [20]) и кусочно-линейная аппроксимация экспериментальных данных (пунктирные линии). Сплошной линией показано изменение площади проекции цилиндрического дефекта при параметрах, восстановленных по опыту с шарообразными пузырьками механического происхождения.

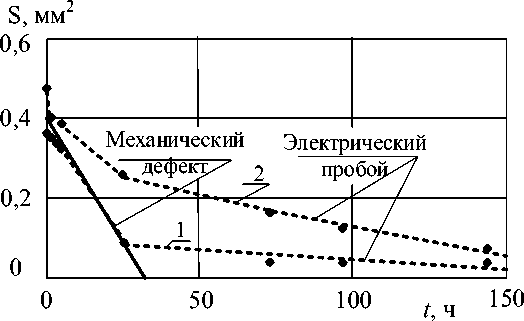
Рис. 2. Изменение площади проекции электрических и механического дефектов от времени

Анализ зависимостей на рис. 2 показывает, что возможны две ситуации. Скорости уменьшения проекции дефекта для эквивалентного механического дефекта (сплошная линия) и для электрического дефекта (пунктирные линии) совпадают. Скорость самовосстановления при электрическом пробое существенно отличается от скорости изменения проекции при механическом дефекте. Меньшая скорость самовосстановления может свидетельствовать о повреждениях поверхностного слоя около дефекта, вызванных электрическим пробоем. Большая скорость самовосстановления может быть вызвана дополнительным процессом, например, контактом изучаемого дефекта с дополнительным (не контролируемым) дефектом.

Наблюдение динамики самовосстановления материала, заключающееся в исчезновении дефекта в виде пузырька, может стать простым и эффективным инструментом анализа для процессов самовосстановления в аморфных материалах, особенно в случаях, когда возможна непосредственная регистрация дефекта по фотографии. Метод позволяет достаточно быстро и напрямую собрать необходимые статистические данные о влиянии различных факторов на эффективность самовосстановления. Анализ состава газов в пузырьке сложно осуществим из-за малого объема пузырька и аморфности материала образца. Высокоэффективная газовая хроматография является дорогостоящим методом и дает только косвенную информацию о состоянии дефекта в момент отбора пробы. Аморфность исследованного материала также является препятствием для анализа дефектов под электронным микроскопом. Поэтому рассмотренный метод фотографирования образца с помощью оптического микроскопа является хорошей альтернативой имеющимся инструментальным методам.

Скорость самовосстановления пузырьков при механическом характере возникновения дефектов является «отправной точкой», относительно которой отсчитывается влияние различных факторов. Наличие «отправной точки» также позволяет избежать проведения дополнительных исследований по измерению растворимости газов, поверхностного натяжения и т. д. Это позволяет более быстро собрать необходимый объем информации при исследовании процесса самовосстановления аморфных прозрачных материалов.

Выводы

Предложена физико-химическая модель, описывающая процесс самовосстановления полимеров, являющихся аморфными прозрачными материалами с дефектами в виде пузырьков. В физико-химической модели учтены процессы растворения газов (водорода, кислорода, азота, моноксида углерода) в материале на основе полисилоксанов и эффекты изменения размеров дефекта за счет сил поверхностного натяжения. Сделан вывод, что совместное действие указанных факторов способствует эффективному самовосстановлению образцов.

С использованием количественной математической модели предложен новый метод оценки эффективности исчезновения дефектов после электрического пробоя, который может опираться на анализ площади дефекта в проходящем через дефект свете по фотографии. Метод заключается в сравнении скорости изменения дефектов механического происхождения со скоростью изменения дефектов после электрического пробоя. Показано, что скорость изменения механических дефектов являются реперным уровнем, который позволяет делать численные оценки влияния различных факторов при электрическом пробое.