Подходы к выделению размерных классов и определению показателей размерной структуры фитопланктонных сообществ Волжского бассейна

Автор: Рисник Д.В.

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Статья в выпуске: 1-4 т.13, 2011 года.

Бесплатный доступ

Предложены методы преобразования численностей клеток фитопланктона различных размеров в интегральный показатель, характеризующий размерную структуру пробы. Предложены принципы разбиения проб на размерные классы, из них выбран принцип, позволяющий оптимально различить влияние на различные показатели размерной структуры факторов, ответственных за экологическое неблагополучие. Методы необходимы для применения показателей с целью биоиндикации качества вод.

Фитопланктон, биоиндикация, размерная структура, размерные классы, группы однородности

Короткий адрес: https://sciup.org/148199761

IDR: 148199761

Текст научной статьи Подходы к выделению размерных классов и определению показателей размерной структуры фитопланктонных сообществ Волжского бассейна

Материалы и методы.

Исходные данные. Для анализа использованы численности и биомассы видов фитопланктона, встречавшихся в протоколах многолетнего (1979-2008 гг.) гидробиологического мониторинга по Нижней, Средней и Верхней Волге . В связи с тем, что гидробиологический мониторинг не всегда предусматривал определение размеров клеток или суммарной биомассы определенного вида наряду с его суммарной численностью [8], был проведен поиск размеров отдельных клеток каждого вида фитопланктона по различным источникам (определители, базы данных в Интернете, частные сообщения, см. . Поскольку о размерах клеток, определенных до рода, и с неопределенным видом невозможно судить по литературным источникам во избежание их возможного вклада, который нельзя учесть, пробу исключали из анализа при относительной численности хотя бы одного такого вида более 3%. При численности менее 3% эти виды не учитывали, т.е. считали их численность равной нулю.

Показатели размерной структуры. В работе рассмотрены следующие показатели:

1) Средний размер клеток в пробе: m = b , где b n

и n – соответственно суммарные биомасса и численность фитопланктона в данном наблюдении.

2) ПРС, характеризующие соотношения между собой размерных классов (крупных, средних, мелких видов) в пробе. Для определения этих показателей необходимо выделение нескольких размерных классов клеток. Разбиение на классы проводили на всем массиве данных Волги. Предложены несколько принципов разбиения на размерные классы (табл. 1).

Таблица 1. Исследуемые принципы разбиения на размерные классы

	Принцип	Недостатки
1	Принцип равной суммарной (по всем пробам Волги) численности видов в классах. Принцип также применим для суммарной биомассы видов.	1. Большой вклад в результаты разбиения могут вносить значения численностей видов с ошибками (на порядок) обусловленными человеческим фактором; 2. Вклад в результаты разбиения проб с малой численностью клеток практически не учтен.
2	Принцип, основанный на размерах клеток тех или иных таксонов. Рассматривали различные комбинации трех границ: 200 мкм³ (верхняя граница размеров мелких одноклеточных Chlorophyta ), 530 мкм³ (верхняя граница размеров клеток колониальных Cyanophyta ), 1000 мкм³ (нижняя граница размеров клеток крупных Euglenophyta и Pyrrophyta )	1. Различные исследователи могут по-разному определять границы; 2. Границы различны для разных водных объектов; 3. Возможность сравнить результаты, полученные разными исследователями и (или) на разных водных объектах спорна.
3	Традиционный принцип, основанный на методе разбиения на равные классы логарифмической шкалы размеров клеток	Не обоснована гипотеза о том, что равные отрезки логарифмической шкалы размеров клеток могут служить критерием разбиения на классы.
4	Принцип, основанный на разбиении каждой пробы на равные по численности размерные классы и усреднении полученных границ по всем пробам. Принцип также применим для биомасс видов.

Расчеты производили для двух, трех и четырех размерных классов. В работе [9] подробно описан подход, основанный на сравнении более крупных классов со всеми более мелкими. Однако в процессе анализа было отмечено, что в ряде случаев при разбиении на три и более размерных класса подход дает некорректные результаты из-за неадекватного вклада классов с нулевой численностью. Этот вклад может приводить к меньшим ожидаемым значениям показателей, иногда вплоть до доминирования более мелких видов над крупными, когда численность крупных видов составляет порядка 80% (рис. 1).

В настоящей работе предложен другой подход, который оценивает соотношение между размерными классами по тангенсу угла наклона прямой, аппроксимирующей методом наименьших квадратов относительные численности (или биомассы) размерных классов в пробе, с последующим отображением тангенса угла в интервал значений показателя от 0 до 1. Этот подход позволяет корректно учесть классы с нулевой численностью клеток. Уравнение прямой, проведенной по методу наименьших квадратов для большего количества точек, описывается системой уравнений:

' N NN

E у x = a E x + b E xi

J i=1 i=1

1 NN

E y i = a E x i + Nb

^ i=1

, где (xi ; yi ) – координаты i-той точки, N – общее число точек, a – тангенс угла наклона прямой, b – свободный член в уравнении прямой.

Тангенс угла наклона прямой соответственно равен:

tg a = a =

E x 2 i = 1

E y i x i i = 1

- E x i E y

N i = 1 i = 1

— E x_t E x i

N i = 1 i = 1

где (xi ; yi ) – координаты i-той точки, n – общее число точек. В нашем случае, например, для разбиения на четыре класса величины xi – это номера классов (1 – мелкие, 2 – средние более мелкие, 3 – средние более крупные, 4 – крупные), а yi – соот- ветствующие относительные численности ( У1 = nм , У2 = nмс , У3 = nкс , У4 = nк ). На Рис. 1 приведена графическая иллюстрация определения tgα в программе MS Excel. Чтобы получить ПРС, изменяющийся в диапазоне от 0 до 1, рассчитанный tgα делили на максимальный его разброс и добавляли слагаемое 0,5.

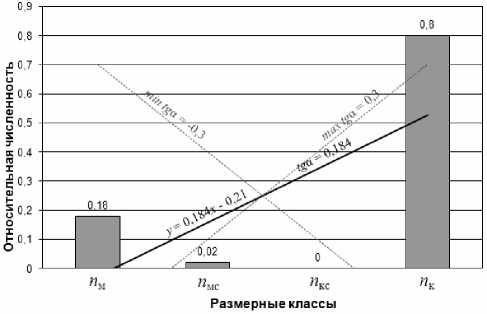
Рис. 1. Определение тангенса угла наклона прямой, аппроксимирующей методом наименьших квадратов относительные численности клеток в четырех размерных классах. По оси x отложены номера размерных классов: 1 – для численности класса мелких клеток, 2 – для средних более мелких, 3 – для средних более крупных, 4 – для крупных

Для обозначения ПРС, характеризующего соотношения численностей размерных классов в пробе, использовали S n . Для обозначения ПРС, характеризующего соотношения биомасс, - S b . Таким образом, для двух классов

n к - n м + 0 5 = 1Х n к + 0 Х n м

2 Х (n к + n м ) , n к + n м

где n и n - соответственно относительные км численности классов крупных и мелких клеток, 2 - максимально возможный разброс всех значений тангенса угла (от -1 до 1), 0,5 - поправка для приведения полученного показателя к положительным значениям. Численность минимального класса с множителем 0 приведена во всех формулах, чтобы подчеркнуть симметричность формулы. Формула для двух классов в этом подходе совпадает с формулой, предложенной в работе [10]. Аналогично для показателя Sb.

Для трех классов

^0,5 ^Х ⁽ n к ^- n м ) + 0 5 ¹ ^х ⁽ n к ⁺ n с ⁺ n м ) ,

1 х n к + 0,5 х n с + 0 х n м n к + n с + n м где nк, nс и nм - соответственно относительные численности классов крупных, средних и мелких клеток, 1 - максимально возможный разброс всех значений тангенса угла (от - 0,5 до 0,5), 0,5 в сумме - поправка для приведения полученного показателя к положительным значениям. Аналогично для показателя Sb .

Для четырех классов:

1Х nк + 23 Х nкс + '3 Х nмс + 0 Х nм n к + n кс + n мс + n м где n , n , n и n - соответственно относи-к кс мс м тельные численности классов крупных, средних более крупных, средних более мелких и мелких клеток. Аналогично для показателя Sb .

Итоговая формула в общем виде:

( N — 1) х n к

S n

⁽ N ^- 1⁾⁽ n к ⁺ ⁿ кс ⁺ ... ⁺ ⁿ м )

₊ ( N - 2) Х n к _С + ... + ( N - N ) Х n м ⁽ N ^- ¹⁾⁽ n к ⁺ n кс ⁺ — ⁺ ⁿ м )

где N - общее число размерных классов.

Группы однородности. Выделение групп однородности производили, исходя из предположения, что размерная структура фитопланктона может зависеть от географического положения водного объекта и сезона года. Чтобы обосновать это предположение необходимо доказать существование групп однородности в исследуемом массиве. Группы однородности ПРС могут быть выделены только при условии, что географические и сезонные вариации оказывают влияние, существенно превосходящее влияние факторов, ответственных за экологическое неблагополучие экосистемы. Если группы однородности существуют, при использовании показателей в биоиндикации возможно локализовать их зависимость от факторов, не влияющих на степень экологического благополучия. По степени отличия групп однородности друг от друга можно судить о преимуществе тех или иных:

1) принципов разбиения на размерные классы, 2) ПРС,

3) количеств размерных классов. Чем сильнее отличие групп однородности, тем лучше локализовано влияние географических и сезонных вариаций.

Для анализа были выделены следующие группы однородности: по отношению к подбассейну (Верхняя (ВВ), Средняя (СВ), Нижняя Волга (НВ)) и по календарным сезонам (весна, зима, лето, осень). Кроме того, были выделены группы однородности по сезонам внутри бассейнов (Весна Вв, Весна СВ, Весна НВ, Лето ВВ, Лето СВ, Лето НВ, Осень ВВ, Осень СВ, Осень НВ, Зима ВВ, Зима СВ). Наблюдения по Нижней Волге в зимний сезон отсутствовали. Также были рассмотрены группы однородности по биологическим сезонам, выделенным на основании однородности видового состава фитопланктона. В марте и апреле преобладали мелкие жгутиковые; в мае и июне - крупные диатомовые; в июле и августе - мелкие зеленые и сине-зеленые; в сентябре, октябре и ноябре - крупные диатомовые; в декабре, январе и феврале - фитопланктона мало. Выделение групп однородности по календарным и биологическим сезонам производили с целью выбора из них лучшего.

При помощи критерия проверки на симметричность и значение эксцесса [11, модификации Д'Агостино] было выявлено, что все ПРС внутри групп однородности не распределены по нормальному закону. Следовательно, для анализа их различий не применимы параметрические методы (тест Стьюдента, дисперсионный анализ). Поэтому для сравнения групп однородности был использован U -параметр Манна-Уитни как непараметрический метод статистического анализа, не требующий нормальности распределения.

Анализ повторностей. Анализ повторностей проводили для того, чтобы различить разбросы ПРС, вызванные различным качеством вод, и разбросы, вызванные погрешностями в отборе и обработке проб. Для анализа были использованы доступные нам по публикациям данные по двум группам повторностей. Первая - 51 повторности отбора проб с поверхности Белого моря в июне 1969 г. в период, когда плотность фитопланктона невелика, и вторая - 50 повторностей отбора проб с поверхности Белого моря в августе 1969 г., когда плотность фитопланктона значительно выше [12]. Поскольку в этих исследованиях производили только подсчет численностей видов без определения биомассы и размеров клеток, размеры клеток были взяты из литературных источников, подобно тому, как это было сделано для волжских видов. После удаления видов, определенных только до рода, остались 11 июньских и 44 августовские пробы. Были выделены границы для двух, трех и четырех размерных классов на основании принципа равнонаполнен-ности классов по численности и по биомассе клеток. Анализ четырех размерных классов по принципу № 1 из табл. 1 оказался невозможным, поскольку численность вида Thalas-sionema nitzschioides составляла в пробах около 50% от общей численности. Анализ по принципу № 2 также оказался невозможным в связи с малым количеством видов в повторностях.

Вопросы исследования. Поскольку вариантов решения задач, сформулированных во введении работы, оказалось несколько, возникли дополнительные вопросы, ответ на которые должно дать настоящее исследование:

1. Выяснить достоверность выделения групп однородности по подбассейнам и сезонам.
2. Выбрать способ выделения групп однородности по сезонам, т.е. оценить какой способ выделения по календарным или биологическим сезонам является более правильным.
3. Выбрать наилучший способ разбиения на размерные классы из двух вариантов – по численности или по биомассе (для принципов 1 и 4).
4. Выбрать наиболее адекватный целям исследования принцип разбиения проб на размерные классы.
5. Выбрать способы разбиения на размерные классы по числу классов – два, три или четыре.
6. Выбрать наиболее полезный из ПРС – m , S n или S b .
7. Сравнить разбросы ПРС внутри групп однородности с разбросами за счет погрешностей в обработке проб.

Результаты и обсуждение. Сравнение принципов разбиения проводили на основании следующих критериев:

1) число случаев нахождения достоверно различных по U -параметра Манна-Уитни с уровнем значимости α = 0,05 групп однородности;
2) степень превышения табличным значением U -параметра Манна-Уитни значения, определенного для групп однородности (свидетельствует о степени различия между группами);
3) число групп однородности, в которых коэффициент вариации значений исследуемого показателя размерной структуры превышал коэффициент вариации аналогичного показателя повторностей проб;
4) степень превышения коэффициента вариации значений исследуемого показателя над

коэффициентом вариации аналогичного показателя повторностей проб.

Для первого и третьего критериев расчеты проводили отдельно для групп однородности: по подбассейнам, по сезонам и по сезонам подбассейнов. Для второго и четвертого критериев в анализе были по отдельности использованы среднегеометрические значения степеней превышения для групп однородности: по подбассейнам, по сезонам и по сезонам подбассейнов. Чем больше значения первых двух критериев, тем лучше локализовано влияние географического положения и сезонов года. Чем больше значения третьего и четвертого критериев, тем меньший вклад в значения ПРС вносят особенности отбора и обработки проб.

Достоверность выделения групп однородности. Обнаружение достоверных различий между выделенными группами однородности по U -параметру Манна-Уитни с уровнем значимости α = 0,05 позволяет утверждать, что группы однородности по географическому положению и сезонам года существуют.

Способ выделения групп однородности по сезонам. На основании вышеприведенных критериев провели выбор лучшего разбиения на сезоны года (лучшего для исключения влияния географических, сезонных и метрологических вариаций). Количество случаев превышения критериев для биологических сезонов было больше случаев превышения для календарных сезонов для каждого из принципов разбиения. На основании этого было принято решение отказаться от выделения групп однородности на основании календарных сезонов.

Способ разбиения на размерные классы по биомассе или численности. Для принципов разбиения на размерные классы по численности и по биомассе (принципы № 1, 4 табл.1.) также было проведено сравнение на основании тех же критериев. Сравнение показало, что для каждого из этих принципов разбиение по численности предпочтительнее разбиения по биомассе по количеству случаев превышения критериев. В дальнейшем анализе разбиения по биомассе не рассматривали.

Принцип разбиения проб на размерные классы. Данные расчетов по описанным критериям для различных принципов разбиения приведены в табл. 2.

При анализе количества случаев превышения критериев одного принципа над другим в равной степени учитывали случаи для S n и S b для разбиения на два, три и четыре размерных класса; для групп однородности по подбассейнам, сезонам и сезонам подбассейнов. На основании данных табл. 2 было проведено ранжирование принципов разбиения по пригодности к выделению групп однородности, локализующих влияние на ПРС географических, сезонных и метрологических вариаций (табл. 3).

Таблица 2. Значения критериев выбора принципа разбиения на размерные классы

№ принципа разбиения из табл. 1.	Группы однородности	Число случаев достоверного различия групп однородности по параметру Манна-Уитни						Средняя степень различия выделенных групп однородности по параметру Манна-Уитни
		2 размерных класса		3 размерных класса		4 размерных класса		2 размерных класса		3 размерных класса		4 размерных класса
		S n	S b	S n	S b	S n	S b	S n	S b	S n	S b	S n	S b
1	по подбассейнам	1	1	0	1	0	1	0,89	0,88	0,82	0,91	0,85	0,96
	по сезонам	3	3	3	3	3	3	0,91	0,87	0,93	0,88	0,91	0,85
	по сезонам подбассейнов	24	22	21	24	21	21	0,98	0,93	1,02	0,97	0,96	0,92
2	по подбассейнам	1	1	0	1	1	1	0,87	0,87	0,82	0,88	0,86	0,87
	по сезонам	2	0	4	2	3	1	0,80	0,76	0,87	0,79	0,85	0,77
	по сезонам подбассейнов	12	9	21	13	20	11	0,83	0,80	0,91	0,84	0,89	0,82
3	по подбассейнам	0	0	2	0	0	0	0,87	0,87	1,21	0,87	0,89	0,86
	по сезонам	4	4	0	1	4	4	0,91	0,86	0,79	0,83	0,91	0,87
	по сезонам подбассейнов	23	21	21	5	21	21	0,96	0,92	0,98	0,85	0,97	0,92
4	по подбассейнам	1	1	1	1	1	1	0,92	0,93	0,88	0,88	0,90	0,89
	по сезонам	3	2	3	2	3	2	0,91	0,87	0,85	0,78	0,88	0,80
	по сезонам подбассейнов	24	22	22	12	23	15	1,03	0,96	0,92	0,81	0,97	0,84
№ принципа разбиения из табл. 1.	Группы однородности	Число групп однородности с коэффициентами вариации, превышающими коэффициенты вариации повторностей						Средняя степень превышения коэффициентов вариации внутри групп однородности над коэффициентами вариации повторностей
		2 размерных класса		3 размерных класса		4 размерных класса		2 размерных класса		3 размерных класса		4 размерных класса
		S n	S b	S n	S b	S n	S b	S n	S b	S n	S b	S n	S b
1	по подбассейнам	3	3	3	3			1,81	7,82	1,58	5,28
	по сезонам	5	5	5	5			2,11	10,90	1,80	6,92
	по сезонам подбассейнов	10	10	10	10			1,83	7,01	1,61	4,94
2	по подбассейнам	3	2	3	3			2,00	1,27	2,12	2,44
	по сезонам	5	5	5	5			1,99	1,50	2,19	2,89
	по сезонам подбассейнов	11	8	11	10			2,01	1,31	2,15	2,52
3	по подбассейнам	3	3	0	3	0	3	2,44	3,64	0,68	2,07	0,90	1,87
	по сезонам	5	5	2	5	2	5	2,46	4,28	0,94	2,71	0,96	2,13
	по сезонам подбассейнов	11	11	2	11	3	10	2,46	3,71	0,75	2,14	0,90	1,85
4	по подбассейнам	3	3	3	3	3	3	2,42	4,85	2,09	7,95	1,72	5,42
	по сезонам	5	5	5	5	5	5	2,61	6,32	2,36	10,36	1,93	7,00
	по сезонам подбассейнов	10	10	11	11	10	11	2,42	4,63	2,16	8,26	1,78	5,60

Примечание: S n – ПРС, характеризующий соотношения численностей размерных классов; S b – аналогичный показатель для биомасс

Таблица 3. Принципы разбиения, ранжированные по количеству случаев превышения критериев одних принципов над критериями других

Принцип X	Принцип Y
Принцип X	4	1	3	2
4		5	29	31
1			20	25
3				9
2

Примечание: в таблице приведено количество случаев превышения критериев для принципа разбиения X над принципом разбиения Y за вычетом количества случаев превышения критериев для принципа Y над принципом X . Отрицательные значения в таблице не приведены. Номера принципов см. в табл. 1.

Лучшим принципом разбиения можно считать принцип №4, основанный на разбиении каждой пробы на равные по численности клеток классы и усреднении полученных границ по всем пробам.

Способы разбиения на размерные классы по числу классов . Лучшим для выделения групп однородности по принципу №4 можно признать разбиение на два размерных класса. Несколько хуже разбиения на три и четыре

размерных класса, которые дают сходные результаты по количеству случаев превышения.

Наиболее полезный из ПРС. Результаты анализа групп однородности по принципу разбиения №4, приведены в табл. 4 и 5. Для заключения о неравенстве двух групп однородности необходимо, чтобы U -параметр был меньше табличного U 0 (также приведены в таблице). Причем, чем меньше U -параметр, тем сильнее различия исследуемых групп.

Таблица 4. Результаты поиска групп однородности по биологическим сезонам года и подбассейнам Волги при разбиении №4 каждой пробы на равные по численности классы и усреднение полученных границ по всем пробам

Группы однородности		U 0 / U							U 0	N
		2 размерных класса		3 размерных класса		4 размерных класса		m
		S n	S b	S n	S b	S n	S b	m
ВВ	НВ	1,21	1,21	1,12	1,17	1,09	1,19	0,79	272804	844	726
ВВ	СВ	0,90	0,91	0,86	0,86	0,88	0,87	0,87	496400	844	1305
НВ	СВ	0,72	0,73	0,70	0,68	0,75	0,69	0,75	425087	726	1305
ДЯФ	ИА	0,70	0,66	0,74	0,70	0,77	0,75	0,84	15533	47	925
ДЯФ	МА	0,85	0,85	0,94	0,95	0,95	0,95	1,14	1494	47	87
ДЯФ	МИ	1,06	0,97	1,01	0,84	1,05	0,89	1,18	15287	47	910
ДЯФ	СОН	0,72	0,69	0,74	0,70	0,76	0,75	0,85	15189	47	904
ИА	МА	0,59	0,57	0,57	0,56	0,59	0,59	0,58	31369	925	87
ИА	МИ	1,91	1,70	1,40	1,05	1,55	1,07	1,24	377631	925	910
ИА	СОН	0,93	0,94	0,92	0,93	0,89	0,92	0,89	375084	925	904
МА	МИ	0,84	0,77	0,66	0,61	0,68	0,62	0,64	30866	87	910
МА	СОН	0,62	0,60	0,58	0,57	0,60	0,58	0,58	30664	87	904
МИ	СОН	1,65	1,50	1,42	1,09	1,51	1,12	1,25	368866	910	904
ДЯФ СВ	ИА ВВ	0,68	0,63	0,70	0,64	0,79	0,68	0,80	4069	38	302
ДЯФ СВ	ИА НВ	0,97	0,88	1,05	0,96	0,99	1,07	1,27	3222	38	238
ДЯФ СВ	ИА СВ	0,66	0,62	0,72	0,64	0,82	0,71	0,82	5158	38	385
ДЯФ СВ	МА СВ	0,77	0,78	0,81	0,80	0,81	0,80	0,95	799	38	59
ДЯФ СВ	МИ ВВ	1,14	1,03	1,15	0,92	1,20	0,95	1,35	3434	38	254
ДЯФ СВ	МИ НВ	1,17	1,03	1,17	0,91	1,18	1,02	1,41	3129	38	231
ДЯФ СВ	МИ СВ	1,03	0,93	1,00	0,78	1,06	0,83	1,18	5679	38	425
ДЯФ СВ	СОН ВВ	0,70	0,66	0,72	0,67	0,83	0,74	0,91	3699	38	274
ДЯФ СВ	СОН НВ	0,91	0,83	0,97	0,81	0,89	0,84	0,99	3142	38	232
ДЯФ СВ	СОН СВ	0,70	0,67	0,70	0,67	0,82	0,73	0,86	5328	38	398
ИА ВВ	ИА НВ	1,35	1,59	1,22	1,80	1,17	1,87	1,37	30012	302	238
ИА ВВ	ИА СВ	0,82	0,83	0,85	0,85	0,88	0,89	0,86	49357	302	385
ИА ВВ	МА СВ	0,62	0,59	0,61	0,59	0,64	0,61	0,61	6705	302	59
ИА ВВ	МИ ВВ	2,05	1,95	1,60	1,36	1,77	1,36	1,47	32115	302	254
ИА ВВ	МИ НВ	2,89	2,37	1,53	1,30	2,02	1,44	1,36	29092	302	231
ИА ВВ	МИ СВ	1,75	1,70	1,27	1,05	1,45	1,14	1,27	54624	302	425
ИА ВВ	СОН ВВ	0,81	0,78	0,83	0,78	0,79	0,96	0,96	34745	302	274
ИА ВВ	СОН НВ	1,29	1,31	1,18	0,66	0,68	0,67	0,71	29223	302	232
ИА ВВ	СОН СВ	0,88	0,92	0,82	0,89	0,88	0,92	0,91	51069	302	398
ИА НВ	ИА СВ	0,59	0,57	0,62	0,56	0,67	0,57	0,60	38502	238	385
ИА НВ	МА СВ	0,72	0,69	0,71	0,71	0,71	0,74	0,69	5288	238	59
ИА НВ	МИ ВВ	1,38	1,16	1,14	0,91	1,23	0,99	0,96	25102	238	254
ИА НВ	МИ НВ	1,90	1,25	1,08	1,05	1,32	1,03	0,84	22750	238	231
ИА НВ	МИ СВ	1,17	1,02	0,91	0,60	1,02	0,61	0,80	42593	238	425
ИА НВ	СОН ВВ	1,27	1,35	1,22	1,47	1,07	1,37	1,08	27148	238	274
ИА НВ	СОН НВ	0,82	0,92	0,83	1,51	0,86	1,49	1,22	22852	238	232
ИА НВ	СОН СВ	0,62	0,62	0,60	0,58	0,68	0,57	0,62	39832	238	398
ИА СВ	МА СВ	0,62	0,60	0,62	0,61	0,65	0,64	0,64	8530	385	59
ИА СВ	МИ ВВ	2,04	1,91	1,67	0,61	1,70	0,63	0,60	41214	385	254
ИА СВ	МИ НВ	2,75	2,24	0,56	0,61	1,92	0,60	0,60	37317	385	231

Продолжение таблицы 4
ИА СВ	МИ СВ	1,76	1,68	1,36	1,08	1,41	1,09	1,28	70262	385	425
ИА СВ	СОН ВВ	0,79	0,77	0,83	0,79	0,81	0,79	0,77	44605	385	274
ИА СВ	СОН НВ	0,62	0,61	0,63	0,66	0,70	0,69	0,71	37486	385	232
ИА СВ	СОН СВ	0,91	0,96	0,89	0,90	0,86	0,90	0,92	65670	385	398
МА СВ	МИ ВВ	0,95	0,88	0,83	0,74	0,85	0,73	0,75	5643	59	254
МА СВ	МИ НВ	0,92	0,79	0,77	0,72	0,81	0,73	0,74	5133	59	231
МА СВ	МИ СВ	0,87	0,81	0,72	0,65	0,75	0,66	0,69	9406	59	425
МА СВ	СОН ВВ	0,63	0,61	0,62	0,61	0,66	0,65	0,65	6086	59	274
МА СВ	СОН НВ	0,76	0,71	0,71	0,66	0,70	0,66	0,63	5155	59	232
МА СВ	СОН СВ	0,66	0,64	0,62	0,63	0,66	0,65	0,64	8815	59	398
МИ ВВ	МИ НВ	0,84	0,89	0,94	0,87	0,88	0,81	0,89	24335	254	231
МИ ВВ	МИ СВ	0,77	0,77	0,70	0,68	0,71	0,72	0,73	45598	254	425
МИ ВВ	СОН ВВ	1,95	1,72	1,62	1,20	1,64	1,12	1,18	29046	254	274
МИ ВВ	СОН НВ	1,21	1,18	1,14	1,01	1,29	1,01	1,33	24445	254	232
МИ ВВ	СОН СВ	1,67	0,59	1,69	0,64	1,61	0,64	0,61	42638	254	398
МИ НВ	МИ СВ	0,76	0,80	0,76	0,68	0,75	0,67	0,81	41279	231	425
МИ НВ	СОН ВВ	2,79	2,00	1,56	1,13	1,88	1,15	1,12	26317	231	274
МИ НВ	СОН НВ	1,33	1,21	1,00	0,91	1,32	1,01	1,08	22156	231	232
МИ НВ	СОН СВ	0,54	0,56	0,55	0,64	0,55	0,62	0,63	38605	231	398
МИ СВ	СОН ВВ	1,66	1,51	1,30	0,95	1,35	0,96	1,04	49357	425	274
МИ СВ	СОН НВ	1,07	1,05	0,90	0,77	1,07	0,83	1,09	41467	425	232
МИ СВ	СОН СВ	1,48	1,37	1,44	1,01	1,36	1,04	1,21	72713	425	398
СОН ВВ	СОН НВ	1,21	1,16	1,19	0,72	1,01	0,76	0,82	26436	274	232
СОН ВВ	СОН СВ	0,84	0,86	0,79	0,82	0,82	0,81	0,80	46149	274	398
СОН НВ	СОН СВ	0,66	0,68	0,61	0,68	0,71	0,70	0,75	38780	232	398

Примечание: в таблице приведено отношение табличных значений (U ₀) U -параметр Манна-Уитни к значениям U , полученным в результате анализа. Обозначения: НВ – Нижняя Волга; ВВ – Верхняя Волга; СВ – Средняя Волга; ДЯФ – декабрь, январь и февраль; МА – март и апрель; МИ – май и июнь; ИА – июль и август; СОН – сентябрь октябрь и ноябрь; S_n – ПРС, характеризующий соотношения численностей размерных классов; S_b – аналогичный показатель для биомасс; m – средняя масса клетки в пробе; N – число проб в группе однородности; жирным шрифтом выделены отношения значений U -параметров, превышающие единицу, соответствующие значимым различиям исследуемых групп

Таблица 5. Коэффициенты вариации внутри групп однородности при разбиении №4 в сравнении с коэффициентами вариации повторностей

Группы однородности	2 размерных класса		3 размерных класса		4 размерных класса		m	N
Группы однородности	S n	S b	S n	S b	S n	S b	m	N
ВВ	0,79	0,55	0,71	0,55	0,55	0,43	1,78	844
НВ	0,47	0,19	0,42	0,20	0,41	0,19	1,01	726
СВ	0,84	0,56	0,75	0,57	0,55	0,42	2,49	1305
ДЯФ	1,00	0,70	0,99	0,69	0,80	0,55	1,60	47
ИА	0,86	0,57	0,73	0,55	0,55	0,42	2,72	925
МА	0,66	0,58	0,64	0,57	0,62	0,55	1,69	87
МИ	0,42	0,26	0,42	0,32	0,35	0,25	1,44	910
СОН	0,88	0,55	0,77	0,54	0,57	0,41	2,18	904

Продолжение таблицы 5
ДЯФ СВ	1,08	0,71	1,05	0,69	0,91	0,59	1,53	38
ИА ВВ	0,99	0,69	0,84	0,66	0,62	0,51	1,35	302
ИА НВ	0,48	0,11	0,42	0,12	0,43	0,11	0,71	238
ИА СВ	1,04	0,71	0,85	0,67	0,57	0,47	3,36	385
МА СВ	0,83	0,72	0,79	0,70	0,76	0,67	1,85	59
МИ ВВ	0,43	0,28	0,44	0,32	0,37	0,27	1,31	254
МИ НВ	0,24	0,06	0,33	0,19	0,26	0,13	1,08	231
МИ СВ	0,51	0,32	0,45	0,37	0,38	0,29	1,70	425
СОН ВВ	0,92	0,61	0,80	0,62	0,57	0,47	2,31	274
СОН НВ	0,65	0,32	0,47	0,26	0,51	0,28	0,76	232
СОН СВ	1,01	0,63	0,96	0,64	0,62	0,44	2,21	398
Повторности 1	0,17	0,08	0,09	0,05	0,10	0,06	0,19	44
Повторности 2	0,28	0,04	0,29	0,04	0,29	0,04	0,44	11

Примечание: обозначения: НВ – Нижняя Волга; ВВ – Верхняя Волга; СВ – Средняя Волга; ДЯФ – декабрь, январь и февраль; МА – март и апрель; МИ – май и июнь; ИА – июль и август; СОН – сентябрь октябрь и ноябрь; Повторности 1 – первая группа повторностей; Повторности 2 – вторая группа повторностей; Sn – ПРС, характери- зующий соотношения численностей размерных классов; Sb – аналогичный показатель для биомасс; m – средняя масса клетки в пробе; N – число проб в группе однородности; жирным шрифтом выделены значения коэффициентов вариации, которые были ниже соответствующих коэффициентов вариации повторностей

Выводы:

1. Группы однородности по сезонам и подбассейнам существуют.
2. Биологические сезоны позволяют локализовать влияние сезонных вариаций лучше календарных сезонов.
3. Разбиение на размерные классы по численности лучше разбиения по биомассе.
4. Наилучшим из анализируемых принципов разбиения является принцип разбиения №4, основанный на делении каждой пробы на равные по численности классы и усреднении полученных границ по всем пробам.
5. Наиболее полезными ПРС можно считать показатели S n и S b .
6. В целом выделение двух размерных классов можно признать более предпочтительным по сравнению с выделением трех и четырех, вместе с тем для дальнейшего анализа было решено не отказываться от выделения трех размерных классов, поскольку оно слабее реагирует на погрешности, обусловленные отбором и обработкой проб.

Проведенный анализ осуществляли с целью дальнейшей биоиндикации состояния вод бассейна Волги по ПРС. Для оценки экологического состояния вод нужно установить для ПРС границу, разделяющую "благополучные" и "неблагополучные" значения показателей. Для определения этой границы необходим одновременный анализ полученных ПРС и физикохимических факторов, влияющих на состояние водной среды. Поскольку в реальных условиях ПРС подвержены одновременному влиянию многих факторов, методы корреляционного анализа в данном случае неприменимы [17]. Для одновременного определения границ нормы экологического благополучия индикаторов и границ нормы факторов, разделяющих "допустимые" и "недопустимые" значения, применяют метод установления локальных экологических норм [1317, см. также http://ecograde.belozersky. library/]. Анализ значений границ

нормы экологического благополучия для ПРС и границ нормы фактора, полученных этим методом на массиве биологических и физикохимических данных по Нижней Волге, будет приведен в последующих публикациях.

Работа частично поддержана грантами РФФИ № 10-04-00013а, 11-04-00915а.

Список литературы Подходы к выделению размерных классов и определению показателей размерной структуры фитопланктонных сообществ Волжского бассейна

Rapport, D.J. Ecosystem behavior under stress/D.J. Rapport, H.A. Regier, T.C. Hutchinson//Am. Nat. 1985. V. 125. P. 617-640.
Левич А.П. Оптимизация структуры кормовых фитопланктонных сообществ. Под ред. проф. В.Н.Максимова/А.П. Левич, Н.Г. Булгаков, Д.Г. Замолодчиков. -М.: Товарищество научных издателей КМК. 1996. 136 с.
Максимов, В.Н. Ранговые распределения размерно-морфологических групп микроводорослей в перифитоне и их связь с уровнем загрязнения водоема/В.Н. Максимов, Н.Г. Булгаков, Л.В. Джабруева//Изв. РАН. Сер. биол. 1997. № 6. С. 697-704.
Каменир, Ю. Влияние антропогенного загрязнения на фитопланктон Каневского водохранилища (Украина). 2. Сравнение размерных спектров/Ю. Каменир, Т.И. Михайлюк, А.Ф. Попова и др.//Альгология. 2008. Т. 18, № 2. С. 145-159.
Девяткин, В.Г. Анализ структуры сообществ водорослей//Водоросли: проблемы таксономии, экологии и использование в мониторинге: Материалы II всероссийской конференции. -Сыктывкар: Институт биологии Коми НЦ УрО РАН, 2009. С. 331-334.
Корнева, Л.Г. Экологические классификации планктонных водорослей//Водоросли: проблемы таксономии, экологии и использование в мониторинге: Материалы II всероссийской конференции. -Сыктывкар: Институт биологии Коми НЦ УрО РАН, 2009. С. 93-96.
Лях, А.М. Обзор методов количественного учета фитопланктона/А.М. Лях, А.М. Суворов, Ю.В. Брянцева//Системы контроля окружающей среды. Сб. науч. тр. НАН Украины. МГИ: -Севастополь, 2002. С. 425-430.
Руководство по гидробиологическому мониторингу пресноводных экосистем/Под ред. Абакумова В.А. -СПб.: Гидрометеоиздат, 1992. 318 с.
Рисник, Д.В. Показатели размерной структуры фитопланктонных сообществ и анализ их изменчивости на фоне сезонных, географических и метрологических вариаций/Д.В. Рисник, А.П. Левич, Н.Г. Булгаков, И.Г. Радченко//Актуальные проблемы экологии и природопользования. Вып. 13: Сборник научных трудов. -М.: РУДН, 2011. С. 171-187.
Булгаков, Н.Г. Биоиндикация экологического состояния по размерной и ранговой структурам фитопланктона водных объектов Московского региона/Н.Г. Булгаков, В.А. Курочкина, А.П. Левич и др.//Бюллетень Московского общества испытателей природы. Отдел биологический. 2009. Т. 4. Вып. 3, Приложение 1. Часть 1. С. 106-114.
Лемешко, Б.Ю. Сравнительный анализ критериев проверки отклонения распределения от нормального закона/Б.Ю. Лемешко, С.Б. Лемешко//Метрология. 2005. № 2. С. 3-23.
Кольцова, Т.И. К вопросу о представительности выборок при анализе фитопланктонных проб/Т.И. Кольцова, Л.А. Конопля, В.Н. Максимов, В.Д. Федоров//Гидробиологический журнал. 1971. Т. 7. №3. С. 109-116.
Левич, А.П. Теоретические и методические основы технологии регионального контроля природной среды по данным экологического мониторинга/А.П. Левич, Н.Г. Булгаков, В.Н. Максимов. -М.: НИА-Природа, 2004. 271 с.
Левич, А.П. Экологический контроль окружающей среды по данным биологического и физико-химического мониторинга природных объектов/А.П. Левич, Н.Г. Булгаков, Д.В. Рисник, Е.С. Милько//Компьютерные исследования и моделирование. 2010. №2. С.199-207.
Левич, А.П. Методические вопросы применения показателей видового разнообразия фитопланктона для анализа качества вод Нижней Волги/А.П. Левич, Д.В. Рисник, Н.Г. Булгаков и др.//Использование и охрана природных ресурсов России. 2010. №5. С.44-48. №6. С. 33-37.
Булгаков, Н.Г. Анализ экологического состояния вод для отдельных створов Нижней Волги на основе биоиндикации по показателям видового разнообразия фитопланктона/Н.Г. Булгаков, Д.В. Рисник, А.П. Левич, Е.С. Милько//Вода: химия и экология. 2010. №12. С.27-34.
Левич, А.П. Нормирование качества среды и биоиндикация экологического состояния природных объектов как детерминационный анализ зависимостей «доза-эффект» для функций многих переменных/А.П. Левич, Е.С. Милько//Актуальные проблемы экологии и природопользования. Сборник научных трудов. М., 2011. Вып. 13. С. 16-25. (http://ecograde.belozersky.msu.ru/library/articles/normi rovanie kachestva sredy.pdf)

Еще

Статья научная