Подсчет предгамильтоновых циклов на семействах решеточных графов

ОБОЗНАЧЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

В работе обсуждаются графы, называемые прямоугольными решетками P_m x P n . Прямоугольная решетка представляет собой целочисленные точки координатной плоскости, связанные по принципу ближайшего соседства. Обозначение P_m х P n связано с тем, что целочисленный прямоугольник суть прямое произведение двух цепей, первая из которых имеет m звеньев, а вторая – n . Число m – ширина решетки (протяженность слева направо), а n – ее длина (протяженность снизу вверх). Поскольку в работе рассматриваются лишь решетки с нечетными сторонами, будем обозначать их символом P 2 _{m +1} х P 2 _n +1 . Максимально возможная длина простого (без самопересечений) цикла в такой решетке на единицу меньше числа ее узлов и равна (2 m + 1)(2 n + 1) – 1. Такой цикл мы будем называть предгамильтоновым. Пример решетки и предгамильтонового цикла в ней показан на рис. 1.

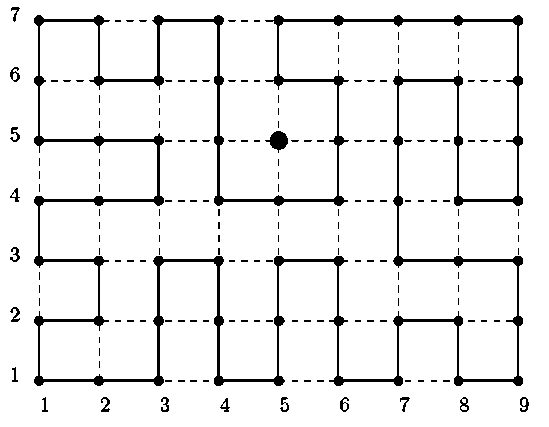
Рис. 1. Решетка P ₉ × P ₇ и предгамильтонов цикл в ней

Задача состоит в том, чтобы для заданных натуральных m и n отыскать количество предга-мильтоновых циклов на решетке P _{2 m +1} х P _{2 n +1}. © Караваев А. М., 2011

Задача не сводится лишь к получению точного числа циклов, а требует изучения предельных свойств модели при неограниченном увеличении общего числа узлов (2 m + 1)(2 n + 1).

Для изучения указанных свойств мы будем обращаться к известным результатам [1], связанным с подсчетом гамильтоновых циклов на решетках P 2 _m +1 х P 2 _n . Все необходимые выводы и факты работы [1] будут повторены здесь для удобства сравнения.

ИЗВЕСТНЫЕ И ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Проблема подсчета гамильтоновых циклов в рассматриваемых семействах графов тесно связана с решением одной из классических задач статистической механики полимеров – подсчетом количества трансформаций плотноупако-ванной макромолекулы [4]. Моделирование таких объектов циклами на решетках относится к классу традиционных методов, основанных на перечислении простых цепей [7].

Однако во всех работах, где плотноупакован-ная макромолекула моделируется гамильтоновой циклом на решетке, то есть циклом, проходящим по каждой вершине ровно один раз, рассмотрены только такие решетки, по крайней мере одна из сторон которых четна, то есть графы вида P 2 _m х P_n и P 2 _{m +1} х P 2 _n. Случаи же решеток с нечетными сторонами P 2 _m +1 х P 2 _n +1 не рассматриваются, так как гамильтоновых циклов в них не существует [10]. Но моделирование плотно-упакованной макромолекулы в этом случае все же возможно – если допустить, что цикл должен пройти по всем узлам решетки, кроме какого-либо одного. Такие циклы, как было сказано выше, мы будем называть предгамильтоновыми. Предгамильтоновы циклы могут также интерпретироваться как циклы на решетке с дефектами. В работе приведены результаты вычисления количества таких циклов на решетках с нечетной стороной, взятого в сумме по всем возможным положениям единственного дефекта.

Цель настоящей работы - заполнить пробел в научной литературе, посвященной вычислительным основам физики полимеров, показав, что вычисления на решетках с нечетными сторонами могут быть проведены немногим сложнее, чем вычисления для хорошо изученных решеток с четным числом узлов, а также расширить известные теоретические выводы в этом случае. Говоря о вычислительных особенностях метода решения задачи, мы постоянно будем ссылаться на авторскую работу [1], в которой дается полное описание алгоритма подсчета гамильтоновых циклов на решеточных графах шириной до 22, а в качестве доказательства того, что предгамильтоновы циклы подсчитываются немногим сложнее, приводим точные результаты расчетов для решеток шириной до 21. Правильность этих результатов не может быть доказана путем строгих математических выкладок, но их неявные подтверждения собраны в разделе «О правильности полученных данных». Отличительная особенность подсчета предга-мильтоновых циклов, которую нужно учесть в описанном в [1] методе, будет обозначена в этой работе в разделе «Схема решения методом матрицы переноса».

Говоря о фактических данных (результатах вычислений) и о выведенных рекуррентных соотношениях, мы будем постоянно отсылать читателя на наш сайт [5], где все эти данные находятся в свободном доступе и никаким образом не могут быть приведены в тексте работы в силу их громоздкости, кроме небольших формул для решеток с небольшой шириной.

Интерпретация полученных результатов позволила сформулировать гипотезу о предельных свойствах модели плотноупакованных макромолекул. Эта гипотеза касается вида главного члена асимптотики и значения константы связности для предгамильтоновых циклов.

Известно [8], что для решеток P2m+1 х P2n с фиксированным параметром m количество гамильтоновых циклов hm (n) асимптотически ведет себя следующим образом n m      ^m mm ,        ’ где цт - некоторая константа, зависящая от ширины решетки. Доказано, что существует предел limm^„2m +1Km = к2. Величина к называется константой связности, и ее вычисление представляет основной интерес, поскольку она непосредственно связана с энтропией, приходящейся на один узел решетки. Считается, но не доказано, что существует предел limm^„2m +1^m = д. Исходя из этого принято считать, что для достаточно больших решеток (как по ширине, так и по длине)

hm (n)» д2 m+1 • к(2 m+1)(2 n).

В настоящей работе показано, что условие га-мильтоновости решетки оказывает сильное влияние на данные оценки. Когда прямоугольная решетка имеет вид P _{2 m +1} х P ₂ n ₊₁ (а параметр m фиксирован), асимптотика количества плотно-упакованных трансформаций р т ( n ) (о чем говорит полученная в статье гипотеза) будет иметь вид

P m ⁽ n )~ ^V m • n • ^K"m , n ^” , где константа v_m , вообще говоря, может отличаться от константы ц т , а их расчет не является целью настоящей работы. Таким образом, сделано предположение, что появление дефекта на решетке добавляет полиномиальный множитель к главному члену асимптотики, но константа связности остается той же самой. Указанная формула строго доказана для m = 1, .„, 5, а предположение о виде главного члена асимптотики для всех натуральных m сформулировано в виде гипотезы в конце статьи.

СХЕМА РЕШЕНИЯ МЕТОДОМ МАТРИЦЫ ПЕРЕНОСА

Наиболее распространенным способом подсчета циклов в сеточных графах является использование метода матрицы переноса [2]. Этот метод уже более полувека успешно применяется для решения различных перечислительных задач, в частности, основные результаты в задаче о подсчете циклов на решетках получены именно методом матрицы переноса (см. сравнение результатов в [1]). Его основное достоинство состоит в том, что он позволяет подсчитать количество циклов в графе без их фактического построения, что особенно важно для задач, принадлежащих классу сложности #Р [11].

Логическая простота метода сводит пробле -му подсчета циклов к вычислению степени матрицы переноса, однако следствием ее вычислительной сложности становится экспоненциальный относительно т рост порядка матрицы. Таким образом, залогом успешного применения метода матрицы переноса является наличие эффективной схемы кодирования состояний и максимально возможное сжатие матрицы путем удаления недостижимых и отождествления идентичных состояний [1].

К сожалению, на сегодняшний день не существует ни одного подхода к решению поставленной задачи, в рамках которого можно было бы вычислить точный ответ для произвольных и достаточно больших значений т и n . Вместо этого решение задачи на решетках начинается с фиксирования одного из параметров. Этим параметром будет т . Таким образом, ширина решетки 2 m + 1 фиксирована, а длина 2 n + 1 будет меняться для n = 1, 2, ... В этом случае может быть применен метод матрицы переноса.

Проиллюстрировать схему метода матрицы переноса удобнее всего на примере решетки ши- риной 3 (когда m = 1). На рис. 2 слева изображена решетка P3 х P7 и предгамильтонов цикл в ней. Справа от решетки изображена последовательность так называемых состояний, через которые проходит цикл, если строить его последовательно снизу вверх, переходя от одного уровня решетки к следующему. Состояние представляет пару из множества дуг и символа «0» или «1». Положение концов дуг указывает на то, как еще не построенный на текущем уровне цикл проходит по вертикальным ребрам этого уровня; символ «0» означает, что до текущего уровня дефект решетки еще не встречался, а «1» – что дефект пройден. Более сложный пример для решетки шириной 5 (когда m = 2) на рис. 2 справа показывает, что дуг в состоянии может быть несколько.

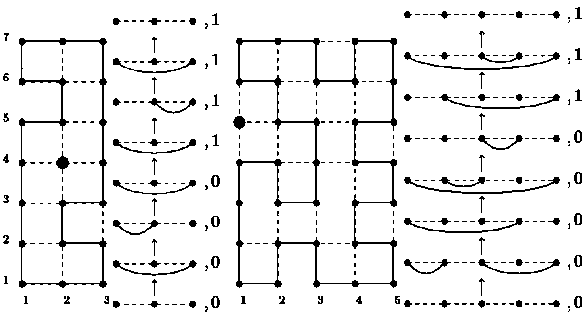
Рис. 2. Решетки P 3 Х P 7 , P 5 Х P ₇ и образующие их состояния

Переход от одного состояния к другому осуществляется путем включения в недостроенный цикл горизонтальных ребер с последующим пе-

реходом к очередному уровню решетки вверх. Для решетки шириной 2 m = 1 для каждого состояния нужно перебрать все 2 ^{2 m} способов установить горизонтальные ребра, чтобы перейти в другие состояния. Всю информацию о том, из каких состояний в какие можно перейти, записывают в матрицу T ( m ), которая называется матрицей переноса. В нашем примере для m = 1 всего 8 возможных состояний, которые указаны на рис. 3. Пронумеровав их в указанном порядке,

случае. Например, для m = 1 из состояния 2 можно перейти в состояние 5 (такой переход есть на рис. 2 слева), значит T ₂₅( 1 ) = 1. Число гамильтоновых циклов на решетке P 3 х P k (для любого натурального k ) равно числу способов перейти от начального состояния 1 (когда построение цикла еще не началось) в конечное состояние 8 (когда цикл замкнулся и дефект пройден) за k шагов. А это число определяется как элемент (1,8) матрицы T (1). Например, на решетке P 3 х P 7 элемент ( T ⁷ (1))₁₈ = 36, таково и количество пред-гамильтоновых циклов на ней.

В самой реализации алгоритма матрица T ( m ) явно не сохраняется, более того, все состояния особым образом кодируются и сжимаются, о чем подробнее написано в [1]. В табл. 1 указаны порядки сжатых матриц переноса для случаев m = 1, 2, …, 10. Например, в случае m = 1 все 8 состояний можно сжать до 3. Это число 3 и указано в табл. 1 в строке m = 1.

Для подсчета предгамильтоновых циклов была написана компьютерная программа, реализующая метод из [1], модифицированный таким образом, чтобы учитывать положение дефекта на решетке. Модификация заключается лишь в том, что для каждого состояния необходимо хранить информацию о том, был ли пройден дефект на решетке или нет. Это немногим более чем вдвое увеличивает число состояний по сравнению с поиском гамильтоновых циклов.

Для сравнения в табл. 1 также выписано число состояний, возникающих в случае подсчета гамильтоновых циклов.

Таблица 1

Порядок сжатой матрицы переноса и рекуррентного соотношения для гамильтоновых циклов на решетках P. . х P, и предгамильтоновых циклов на 2m+1      2n решетках P2m+i х P2n+i

запишем возможные переходы между ними

в матрицу переноса

( 0

0 ^

( 0

36 ^

T (1) =

, T ⁷ (1)

=

.

1:

	Порядок матрицы переноса		Порядок соотношения
	P 2 m +1 Х P 2 n	P 2 m +1 Х P 2 n +1	hm ( n )	pm ( n )
1	2	3	1	2
2	8	12	3	6
3	37	67	18	36
4	213	416	104	208
5	1332	2752	671	1342
6	8 916	19 189
7	62 121	138 205
8	446 483	1 020 530
9	3 284 418	7 678 732
10	24 620 184	58 671 018

О ПРАВИЛЬНОСТИ ПОЛУЧЕННЫХ ДАННЫХ

,о

2:

,о

3:            • ,0

4:

,о

бгч^+^л,! 6:^л — • ,1 7:*—-*^,1 8:* —♦—♦,!

Рис. 3. Все возможные состояния для решетки шириной 3

Элемент T_ij ( m ) = 1, если можно перейти из состояния i в состояние j и T_ij ( m ) = 0 в противном

Правильность метода матрицы переноса доказана в [2], а правильность работы нашего метода, описанного в [1], вытекает из самого построения матрицы переноса: программа перебирает абсолютно все возможные состояния и рас-

считывает все возможные переходы между ними посредством полного перебора. Число таких состояний, указанное в табл. 1, не слишком велико для современных вычислительных систем, однако оно существенно меньше, чем число всевозможных циклов (табл. 2), перечислить которые полным перебором, считая их по одному, невозможно.

Таблица 2

Количество предгамильтоновых циклов на квадратной решетке P 2n +1 x P 2n +1

n

Количество предгамильтоновых циклов

425577772\

Правильность работы самой программы, реализующей метод, не может быть доказана строго, поскольку является объектом вольного творчества ее автора. Однако косвенные проверки показывают, что, по-видимому, программа работает правильно. Например, число циклов на решетках ^P 2 m +1 X ^P ,+1 И ^P 2 n +1 X P 2 m +i должно быть одинаковым. Действительно, оно получилось одинаковым для тех решеток, на которых проводились расчеты, в чем можно убедиться, взяв фактические данные с нашего сайта [5]. Анализ результатов, проделанный ниже, дает вполне закономерный итог: если ширина решетки фиксирована, а длина неограниченно растет, то можно предположить, что число предгамильтоновых циклов на решетке P 2 _{m +1} x P 2n +1 с точностью до константы в n раз больше, чем число гамильтоновых циклов на решетке P 2m ₊₁ x P 2n , так как дефект может занимать любой из (2 m + 1)(2 n +1) узлов. Как мы увидим далее, именно это и подтвердилось для тех случаев, для которых удалось провести точные вычисления.

АНАЛИЗ РЕКУРРЕНТНЫХ СООТНОШЕНИЙ И ПРОИЗВОДЯЩИХ ФУНКЦИЙ

Несмотря на то что метод матрицы переноса является более эффективным способом подсчета циклов в сеточных графах, чем метод полного перебора, в силу самой природы рассматриваемой задачи он оказывается чрезвычайно ресурсоемким и не может быть использован при повседневных расчетах. Крайне желательно иметь более компактное представление для результатов, полученных этим методом.

К счастью, природа самого метода матрицы переноса такова, что полученные с его помощью числовые последовательности будут удовлетворять линейным рекуррентным соотношениям с постоянными коэффициентами. Наличие такой возможности, являющейся следствием теоремы Кели – Гамильтона, позволяет, в частности, оценить сверху порядок рекуррентного соотношения порядком матрицы переноса.

Обозначим число предгамильтоновых циклов на решетке P 2m ₊₁ x P 2n ₊₁ символом P_m ( n). Последовательность чисел p_m ( n ) будет удовлетворять линейному однородному рекуррентному соотношению с постоянными коэффициентами

N m

P m ⁽ n ) = Е c k ‘ P m ⁽ n - ^k ) n >  ^Nm ’ k = 1

причем порядок этого соотношения (который мы обозначили как N_m ) не будет превосходить порядок матрицы T ( m ). Механизм восстановления рекуррентного соотношения по начальному отрезку последовательности сводится к методу неопределенных коэффициентов: зная числа p_m ( n ) в достаточном количестве, можно составить систему линейных уравнений относительно неизвестных c_k и решить ее. Система уравнений получается подстановкой чисел p_m ( N_m + 1), p_m ( N_m + 2), … в рекуррентное соотношение:

P m ^{( N}m )

P m ^{( N}m + 1)

I P m (2 N m - 1)

P m ^{( N}m — 1)   -

P m ^{( N}m )    -

P m ⁽¹⁾

P m (2)

P m (2 N m — 2) - P m ( N m ).

X

c N m

^{Pm ( N}m + 1)

P m ( ^Nm + ² )

.

I P m (2 N m ) J

Поскольку для восстановления коэффициентов c ₁, c ₂, c_N …, требуется удвоенное количество членов п ^m оследовательности, рекуррентное соотношение будет гарантированно правильным, если количество известных чисел p_m ( n ) не меньше удвоенного порядка матрицы переноса. Поэтому основной задачей здесь является получение достаточно длинной последовательности чисел (табл. 1). В настоящем исследовании были получены новые рекуррентные соотношения для случаев m = 1, …, 5. В силу громоздкости полученных выражений детально рассмотрены лишь примеры для m = 1, 2, в то время как остальные выведенные рекуррентные соотношения и начальные данные к ним свободно доступны для скачивания на авторском сайте [5].

В нашем примере для m = 1 последовательность p_m ( n ) для n = 1, 2, 3, … имеет вид 5, 14, 36, …, а рекуррентное соотношение имеет порядок 2 [5]:

P i ⁽¹⁾ = 5, P i ⁽²⁾ = 14, P _t( n ) = 4 p , ( n — 1) — 4 p , ( n — 2), n >  ².

Любому линейному рекуррентному соотношению с постоянными коэффициентами соответствует рациональная производящая функция, которая генерирует точно такую же последовательность. Изучать предельные свойства последовательности удобнее именно через производящие функции. Если ввести обозначение G_m ( z )

для производящей функции, соответствующей рекуррентному соотношению для решеток P2m+i х P2n+1, то, например, для m = 1 она будет иметь вид

G 1 ( z ) = 5 z + 14 z ² + 36 z ³ + •

z (5 - 6 z )

- (1 — 2 z )²

Асимптотика количества предгамильтоновых циклов определяется поведением функции вблизи единственного полюса z = 1/2, который имеет кратность 2. Обратную величину к главному корню знаменателя производящей функции G_m ( z) будем обозначать к_т, то есть к ₁ = 2. Из этого следует, что p ₁( n ) ~ v ₁ • n • 2 ⁿ при n ^ “ . То есть количество предгамильтоновых циклов растет экспоненциально с ростом длины решетки, но, помимо экспоненты, главный член асимптотики имеет полиномиальный множитель-Вычисление значения константы v ₁ в цели нашей работы не входит, но при необходимости его можно определить приближенно, рассчитав отношение p ₁( n )/( n • 2 ⁿ ) для достаточно большого значения n . Так, для n = 500 получим 1,003000...

Мы проиллюстрировали схему анализа полученных рекуррентных соотношений на примере решетки шириной 3, чтобы иллюстрация не оказалась слишком громоздкой. В этом случае решение может быть найдено в виде явной формулы. Разложение производящей функции G ₁( z ) в ряд по степеням z дает явное выражение для коэффициента при zⁿ :

P i ( n ) = ^ n + - J- 2 ⁿ , из которого сразу видно, что v ₁ = 1 и что p ₁( n ) ~ ~ n • 2 ⁿ при n ^ “ . К сожалению, явные формулы для случаев т > 1 не могут быть получены в столь компактной форме, но тогда вполне применим метод анализа, описанный выше.

Интересная особенность производящих функций для числа предгамильтоновых циклов на решетках P2т+1 х P2n+1 проявляется в их сравнении с производящими функциями для числа гамильтоновых циклов на решетках P х P , ко-2 т+1      2 n торые мы обозначим через Hm(z) (о поиске таких циклов подробно написано в [1]). Зная рекуррентные соотношения для числа гамильтоновых циклов на решетках с нечетной шириной до P13 х х P2n [1], мы точно так же можем построить производящие функции Hm(z). Указанная особенность состоит в том, что знаменатель производящей функции Gm(z) является квадратом знаменателя Hm(z) для всех рассмотренных случаев вплоть до m = 5, а главный (минимальный по модулю) корень знаменателя H (z) является простым. Например, в случае m = 1, то есть на решетке P3 х P2n, рекуррентное соотношение для числа гамильтоновых циклов имеет вид [5]

h1(1) = 1, h(n) = 2h1(n -1), n > 1, а производящая функция, соответственно,

H (z) = z + 2 z2 + 4 z3 + - = —^—.

• ¹                            1 - 2 z

Как видно, знаменатель G ₁( z ) равен квадрату знаменателя H ₁( z ).

Аналогичные результаты получаются для случаев m = 2, 3, 4, 5. В этом можно убедиться, взяв все фактические данные (рекуррентные соотношения и начальные данные для гамильтоновых и предгамильтоновых циклов) на нашем сайте [5]. Например, для m = 2

H 2 ( z ) =

z - (1 + 3 z )

1 - 11 z - 2 z³

и

G 2 ( z ) =

2 z - (7 - 41 z + 9 z ² + 4 z ³ + 6 z ⁴ - z ⁵)

( 1 - 11 z - 2 z ³ ) ²

Асимптотика коэффициентов разложения рациональной производящей функции в ряд Маклорена определяется минимальным корнем знаменателя. Он может быть найден точно, но в целях экономии мы его округлим: z ~ 0,0907731. Обратная величина к2 » 11,01648. Для знаменателя H2(z) корень является простым (оба других комплексные), что дает право записать hm(n)~p2 -11,01648n, pm(n)~v2 -n-11,01648n при n ^ да .

Константы p ₂ » 0,115149 и v ₂ » 0,605767 также определяются приближенно, если это необходимо. Во всех остальных случаях ( m = 3, 4, 5) исследование также показало, что главный корень знаменателя H_m ( z ) является простым, а знаменатель G_m ( z ) является квадратом знаменателя H_m ( z ). Вышесказанное позволяет сформулировать гипотезу о том, что данное наблюдение справедливо для всех натуральных m . Мы сформулируем ее в иной форме в заключении.

В табл. 1 указаны порядки рекуррентных соотношений (а значит, и степени знаменателей производящих функций) для гамильтоновых и предгамильтоновых циклов. Эти порядки отличаются в два раза.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

Полученные результаты позволяют сформулировать следующую гипотезу. Если число гамильтоновых циклов h_m ( n ) на решетке P _{2 m +1} х P _{2 n} имеет скорость роста h m ^{( n} )~ M m ^{- K} m при n ^ “ , то число предгамильтоновых циклов p_m ( n ) на решетке P _{2 m +1} х P _{2 n +1} имеет скорость роста ^pm ^{( n} ) ~ ^v m ^{- n - K} m . Основание показательной функции этих асимптотик одно и то же и зависит только от ширины решетки. Вид главного члена асимптотики получен точными методами для m = 1, .„, 5; гипотеза утверждает, что такой вид будет сохраняться для всех натуральных m .

Интересной представляется проверка гипотезы до m = 10 с помощью методов аппроксимации числовых последовательностей [6], но это не входило в цели нашей работы. Однако наш метод позволяет получить последовательности чисел p_m ( n ) для решеток шириной до 21, что подтверждается результатами, приведенными в табл. 2.

В статистической механике полимеров [8] доказано существование предела lim m ^„ ² m + 1 ^ ^ = к² для случая гамильтоновых циклов, следовательно, если гипотеза верна, то величина κ – универсальная константа связности – одна и та же для гамильтоновых и предгамильтоновых циклов.

Показано, что расчет асимптотических свойств плотноупакованных трансформаций полимеров должен проводиться с учетом характеристик среды: если среда моделируется решеткой с дефектами или не обладает свойством гамиль-тоновости, то это влияет на скорость роста возможных трансформаций и, следовательно, на термодинамические свойства модели.

В работе [1] заявлены точные значения числа гамильтоновых циклов для решеток размером до P22 х P 100 и рекуррентные соотношения для решеток шириной до 14. В настоящем исследовании были получены точные значения количества предгамильтоновых циклов на квадратных решетках с нечетными сторонами до P21 х P21. Результаты указаны в табл. 2, а также зарегистрированы в энциклопедии целочисленных последовательностей [9] под номером A181584. Получены рекуррентные соотношения для решеток шириной до 11. Расчеты проводились на кластере Карельского научного центра [3]. Можно проверить справедливость наших выводов с помощью систем компьютерной алгебры, взяв все фактические данные с нашего сайта [5], а также перепроверить наши расчеты, реализовав самостоятельно алгоритм, подробно описанный в [1] с незначительными изменениями касательно положения дефекта, описанными в настоящей работе.

Далее планируется изучить свойства простых циклов максимальной длиной на решетках с более чем одним дефектом. Мы предполагаем, что главный член асимптотики для числа таких циклов будет содержать множителем полином той степени, каково количество дефектов.