Подтверждение обобщенного критериального уравнения конвективного теплообмена для пористых структур экспериментальным путем

Введение. В теории теплообмена изучаются закономерности переноса теплоты из одной области пространства в другую.

Теплообмен или теплопередача – это самопроизвольный процесс обмена внутренней энергией на микроскопическом уровне между телами (или частями тела) с различной температурой [1]. Величина передаваемой при этом внутренней энергии называется теплотой процесса или просто теплотой .

Существуют три механизма распространения теплоты: тепловое излучение, кондукция (теплопроводность) и конвекция.

Конвекция возможна только в текучей среде – газах, жидкостях. Под конвекцией теплоты понимают процесс переноса тепловой энергии в результате перемещения объемов жидкости или газа в пространстве из области с одной температурой в область с другой. При этом перенос теплоты связан с переносом самой среды [1].

Конвекция всегда сопровождается теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом. Конвективный теплообмен между потоком газа (или жидкости) и поверхностью твердого тела называют конвективной теплоотдачей [1]. Важнейшую роль конвективная теплоотдача играет в разнообразных теплообменных устройствах, широко применяется для организации охлаждения теплонапряженных узлов и систем в различных конструкциях [2].

Виды конвекции, критериальные уравнения. Интенсивность процесса теплоотдачи в значительной степени зависит от природы возникновения движения среды [3]. Соответственно, различают естественную и вынужденную конвекцию.

Естественная конвекция (свободное движение) возникает за счет разности плотностей нагретых и холодных объемов жидкости.

Вынужденная конвекция (принудительное движение) создается внешним источником – насосом, вентилятором, поршнем и т.д.

При практических расчетах конвективной теплоотдачи важная роль отводится определению среднего коэффициента конвективной теплоотдачи αV [4,5]. Он зависит от физических свойств охлаждающей среды, конфигурации и размеров поверхности теплообмена и от условий обтекания ее охлаждающей средой [6] и определяется с помощью эмпирических уравнений. Эти уравнения носят название критериальных уравнений (уравнений подобия) и получаются, как уже было указано, экспериментальным путем. В общем случае такие уравнения имеют следующий вид [1].

При естественной конвекции:

Nu=c·Grⁿ·Pr^m .

При вынужденной конвекции:

Nu=c·Reⁿ·Pr^m .

В представленных уравнениях c , n , m – постоянные безразмерные числа, определяемые при обработке опытных данных, а Nu , Gr , Re , Pr – соответственно, критерии Нуссельта, Грасгофа, Рейнольдса и Прандтля.

Критерии Нуссельта, Грасгофа, Рейнольдса и Прандтля представляют собой безразмерные комплексы следующих величин [7]:

Nu =α V ·l 0 /λ T ;                  Gr = g ∙β∙( T С – T Ж )∙ l 0 ³ /ν ² ;

Re =υ∙ l₀ /ν;                    Pr =ν/ a.

В приведенных уравнениях l₀ – определяющий размер тела (стенки), λ_T – коэффициент теплопроводности охлаждающей среды, который выбирается по справочной литературе при температуре хладагента T_Ж , g – ускорение силы тяжести, β=1/ T_Ж – температурный коэффициент объемного расширения охлаждающей среды, T С – температура поверхности тела (стенки), ν – коэффициент кинематической вязкости охлаждающей среды, который выбирается по справочной литературе при температуре хладагента T Ж , υ – скорость движения охлаждающей среды относительно тела (стенки), a – температуропроводность охлаждающей среды.

Физический смысл и области применения критериев Нуссельта, Грасгофа, Рейнольдса и Прандтля следующие [7].

Критерий Нуссельта – это безразмерный коэффициент теплоотдачи. Он характеризует соотношение между интенсивностями конвективной теплоотдачи и теплопроводности в пограничном слое потока. Применяется в исследованиях теплообмена при конвекции.

Критерий Грасгофа – это критерий термогравитационной конвекции. Он характеризует соотношение сил молекулярного трения и подъемной силы, обусловленной различием плотностей в различных точках. Применяется в исследованиях теплообмена при конвекции.

Критерий Рейнольдса – это критерий режима течения. Он характеризует гидродинамический режим потока и определяет соотношение в нем сил инерции и молекулярного трения. Применяется при изучении вынужденных конвективных течений.

Критерий Прандтля – это критерий подобия температурных и скоростных полей. Он характеризует меру подобия скоростных и температурных полей. Характеризует также свойства теплоносителей. Применяется в исследованиях теплообмена при конвекции.

Как уже отмечалось выше, с помощью критериальных уравнений определяется средний коэффициент конвективной теплоотдачи αV.

Внутрипоровый конвективный теплообмен. Одним из перспективных и эффективных способов интенсификации тепломассообменных процессов является использование в разнообразных теплообменных устройствах пористых металлов [8-10]. Широкий диапазон структурных, теплофизических, гидравлических, химических, оптических и других свойств пористых материалов [11], относительная простота изготовления из них элементов конструкций, высокая интенсивность теплообмена дают возможность использования пористых теплообменных элементов в различных экстремальных условиях.

При расчетах, проводимых для пористых элементов конструкций, интенсивность внутрипорового конвективного теплообмена принято характеризовать объемным коэффициентом теплоотдачи h_V из-за невозможности определения участвующей в теплообмене площади внутренней поверхности материала [12]. В таблице 1 приведены некоторые результаты экспериментов по определению коэффициента h V внутрипорового конвективного теплообмена в различных пористых металлах [12].

Экспериментам были подвергнуты проницаемые матрицы, изготовленные из порошков с зернами различных форм и размеров, волокон и сеток разных металлов. Основная часть данных получена для образцов толщиной не более 5 миллиметров. Теплоносителями служили, в основном, воздух или различные газы, значительно реже – масло и спирт. Диапазон численного изменения критерия Рейнольдса Re был достаточно широк – 0,0003…500 (в различных экспериментах – различные участки указанного диапазона). Виды нагрева образцов были также разнообразными: индукционный, омический, радиационный, нестационарный.

Анализ исследований внутрипорового конвективного теплообмена, рекомендованное обобщенное критериальное уравнение. При анализе данных виден значительный разброс результатов. Основные причины этого следующие.

Во-первых, отсутствие единства в выборе характерного размера для числа Re при расчете критериев. В таблице 1 приведены данные с использованием различных параметров, таких как: отношение инерционного β к вязкостному α коэффициентов гидравлического сопротивления β/α [13-15], средний диаметр частиц исходного порошка dЧ, средний диаметр пор dП [16]. Параметр β/α может быть определен достаточно точно, а погрешность в определении dЧ и dП доходит до 20%. Кроме того, затруднительно выбрать характерный размер (иной, чем β/α) для проницаемых непорошковых металлов – из волокон, спиралей, сеток, вспененных.

Таблица 1 – Результаты экспериментов по исследованию внутрипорового конвективного теплообмена

Критериальное уравнение теплообмена	Форма представления		Порист ость, П	Автор, год
	Nu	Re
Nu =0,0286∙ Re 1,84	h V (β/α)2/λ T	G (β/α)/μ	0,3	Дружинин С.А., 1961
Nu =0,006∙ Re 1,84	h V (β/α)2/λ T	G (β/α)/μ	0,52	Дружинин С.А., 1961
Nu =0,005∙ Re·Pr	h V (β/α)2/λ T	G (β/α)/μ	0,3	Максимов Е.А. и др., 1971
Nu =0,007∙ Re 1,2	h V (β/α)2/λ T	G (β/α)/μ	0,37; 0,45	Косторнов А.Г. и др., 1970
Nu~Re 0,9	h V (β/α)2/λ T	G (β/α)/μ	0,31…0, 44	Smith I.E. и др., 1971
Nu =0,0092∙ Re 1,34	h V (β/α)2/λ T	G (β/α)/μ	0,29…0, 601	Щукин В.К. и др., 1976
Nu~Re	h V d Ч 2/ 6λ T (1- П )	Gd Ч /μ П	0,33…0, 39	Crootenhuis P., 1959
Nu= 0,0042∙ Re 0,9	h V d Ч 2/ 6λ T (1- П )	Gd Ч /μ П	0,35	Харченко В.Н., 1968
Nu =0,0175∙ Re·Pr	h V d Ч 2/ 6λ T (1- П )	Gd Ч /μ П	0,33	Бойко А.Н. и др., 1972
Nu =0,09∙ Re	h V d Ч 2/ λ T	Gd Ч /μ	0,31	Максимов Е.А. и др., 1972
Nu =0,1( Re·Pr )1,25	h V d Ч 2/ λ T	GdЧ /μ	0,23…0, 31	Ерошенко В.М. и др., 1975
Nu =0,028 Re 1,2 П 2,9	h V d П 2/ λ T	Gd П /μ П	0,25; 0,32; 0,40	Поляев В.М. и др., 1969

Во-вторых, различие методик обработки результатов [17,18]. При определении величины hV очень сложно измерить температуру охладителя при входе его в пористый материал. В очень тонком слое перед пористым каркасом она резко повышается. В результате теплоноситель получает теплоту до входа в образец, что приводит к значительному завышению объемного внутрипорового коэффициента теплоотдачи hV. Это особенно заметно в образцах с незначительной толщиной. А как уже говорилось выше, подавляющее большинство результатов в таблице 1 получено для матриц толщиной менее 5 миллиметров, что и дает зависимость hV от толщины образца, если включить ее в явном виде в критериальные уравнения теплообмена. Специально проведенные эксперименты для широкого диапазона толщин образцов не выявили подобной зависимости [12].

С учетом изложенного можно отметить, что значительную часть критериальных уравнений для внутрипорового конвективного теплообмена можно использовать только в качестве первого приближения. На основе анализа и обобщения всех данных для предварительных расчетов было рекомендовано [12] следующее критериальное уравнение:

Nu =0,004∙ Re·Pr.

В качестве характерного размера принята величина β/α, расчет которой для металлов из частиц заданного размера и любой формы можно производить с использованием соответствующих зависимостей [12].

Эксперименты для подтверждения обобщенного критериального уравнения внутрипорового теплообмена. В данной статье приведены результаты успешной попытки подтверждения предложенной в работе [12] представленной выше критериальной аналитической зависимости.

В работах [19,20] для расчета температурного поля обогреваемой непроницаемой оболочки на стыке с пористым каркасом приведена математическая модель, которая завершается критериальным уравнением

Nu=0,004∙Re·Pr, в котором критерии Нуссельта, Рейнольдса и Прандтля соответственно определяются следующим образом:

Nu = h_V (β/α) ² /λ_T, Re=G (β/α)/μ, Pr =μ c_P /λ_T.

Тогда это критериальное уравнение при удельном расходе хладагента G и его изобарной теплоемкости c P можно переписать в виде для расчета интенсивности объемного внутрипорового теплообмена:

h V = 0,004 Gc P /(β/α).

В ходе работы были получены и сравнены расчетные и экспериментальные данные.

Экспериментальные модели представляли собой цилиндрические пористые вставки, заключенные между двумя непроницаемыми цилиндрическими оболочками (рисунок 1). Проницаемая матрица изготавливалась из пакета нержавеющих сеток П60 (ГОСТ 3187-76). Материал – сталь 12Х18Н10Т. Пористость моделей варьировалась в диапазоне 0,34…0,36, длина – 5, 10 и 15 миллиметров. Охладителем служил воздух, прокачиваемый нормально к плоскостям слоев сеток.

[22,23].

Рисунок 1 – Экспериментальные образцы с термопарами Автором от эскизного проекта до воплощения в металле была

разработана конструкция экспериментального участка [21], который в разобранном виде представлен на рисунке 2.

Рисунок 2 – Экспериментальный участок в разобранном виде

Разработанный и изготовленный экспериментальный участок монтировался в установку (рисунок 3) для исследования теплообмена и гидравлики в секционных пористых теплообменных трактах (СПТ)

Рисунок 3 – Экспериментальная установка для исследования СПТ

Экспериментальные исследования проводились на стенде в Московском государственном техническом университете им. Н.Э. Баумана. Вид бокса с экспериментальной установкой представлен на рисунке 4. Нагрев моделей осуществлялся высокотемпературным газовым потоком, протекающим по внутренней непроницаемой трубе.

Рисунок 4 - Экспериментальный стенд

Обработка результатов экспериментов и вывод. Для обработки экспериментальных данных при плотности теплового потока q , толщине стенки δ и коэффициенте динамической вязкости μ использовались следующие критериальные соотношения [22,24]:

^а v = q /5( T c ^-т ж ), Nu =а V ф/а) ² /^, Re=G ф/а)/ц.

На рисунке 5 в логарифмических координатах представлено сравнение расчетных и экспериментальных данных, и хорошо заметна их удовлетворительная согласованность.

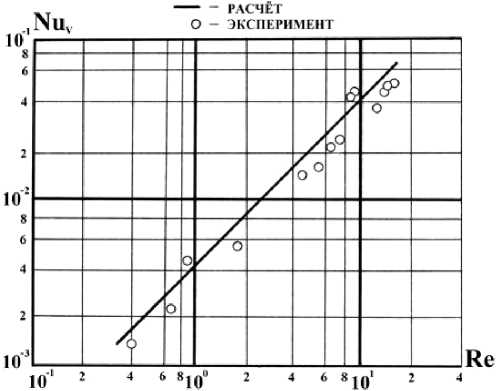
Рисунок 5 – Зависимость критерия Nu от числа Re

Таким образом, в данной работе экспериментально подтверждена возможность использования зависимости Nu =0,004∙ Re·Pr для расчетов, связанных с внутрипоровым конвективным теплообменом, применительно к существующим маркам пористых сетчатых материалов.