Подтверждение требований к надежности новых модификаций разгонных блоков типа ДМ с учетом результатов эксплуатации прототипов

ЗАДЕБА В.А.

Постановка задачи

Одной из задач, решаемых при создании изделий ракетно-космической техники, является выбор критериев для принятия решения о завершении летных испытаний (ЛИ) с точки зрения выполнения количественных требований к надежности.

Количество пусков в рамках ЛИ, как правило, недостаточно для подтверждения требований к вероятности безотказной работы (ВБР) только стандартными методами математической статистики.

Если изделие создается как модификация на основе ранее разработанных прототипов, близких по составу, конструкции, технологии изготовления и подготовки к пуску, имеющих большой объем статистических данных по результатам испытаний и эксплуатации, то естественно учитывать такие данные при подтверждении надежности новой модификации изделия.

Однако, напрямую объединять статистические данные по результатам испытаний можно лишь при условии принадлежности этих данных к одной генеральной совокупности.

Характерным примером изделий, для которых эта задача представляет интерес, является семейство разгонных блоков (РБ) типа ДМ, разработанных РКК «Энергия».

Всего было создано 11 модификаций блоков ДМ (рис. 1), отличающихся по конструкции и составу бортовых систем, но все они в значительной степени базируются на общих проектноконструкторских решениях, принятых при создании исходной модификации — блока Д (изделия 11С824), который эксплуатировался в 1967–1975 гг. в составе ракеты космического назначения (РКН) «Протон-К».

Различия между модификациями РБ обусловлены в основном совершенствованием энергетических характеристик, заменой устаревающей радиоэлектронной аппаратуры, доработками, связанными с адаптацией к ракетам-носителям (РН) и выводимым полезным нагрузкам.

В ходе летной отработки и штатной эксплуатации разгонных блоков типа ДМ накоплена большая статистика. По состоянию на начало 2014 г. — 287 пусков, подавляющее большинство из которых были успешными.

В настоящее время РКК «Энергия» изготавливаются три модификации РБ: ДМ- SL , ДМ- SL Б и 11С861-03 первого этапа для применения в составе РН космического назначения «Зенит-3 SL », «Зенит-3 SL Б» и «Протон-М» соответственно. РБ 11С861-03 первого этапа с декабря 2010 г. проходит ЛИ в составе РКН «Протон-М».

Формально из-за различий по конструкции и составу указанных модификаций разгонных блоков статистические данные по результатам пусков для количественной оценки надежности должны учитываться отдельно для каждой модификации. В этом случае предшествующий опыт эксплуатации прототипов явно не учитывается, что приводит к увеличению количества ЛИ, необходимых для подтверждения требований к вероятности безотказной работы разгонных блоков в полете. Количество летных испытаний новых модификаций можно сократить, если использовать априорную информацию о надежности прототипов.

В данной статье рассмотрен один из возможных методических подходов к решению задачи объединения результатов испытаний вновь создаваемых разгонных блоков с результатами эксплуатации прототипов, который в сочетании с применением последовательного плана для контроля вероятности безотказной работы разгонных блоков позволяет уменьшить необходимое количество летных испытаний.

Блок Д (исходная модификация)

Разгонные блоки типа ДМ

11С824
j^j^^l
Эксплуатация	1967...1975 гг.
Тип РН	«Протон-К»
Количество запусков	38
Отказы РБ	4
Аварии, не связанные с работой РБ	2

11С86
Эксплуатация	1974...1990 гг.
Тип РН	«Протон-К»
Количество запусков	66
Отказы РБ	0
Аварии, не связанные с работой РБ	5

11С824М
Эксплуатация	1975...1990 гг.
Тип РН	«Протон-К»
Количество запусков	12
Отказы РБ	0
Аварии, не связанные с работой РБ	0

11С861
Эксплуатация	1982...2012 гг.
Тип РН	«Протон-К» «Протон-М»
Количество запусков	103
Отказы РБ	4
Аварии, не связанные с работой РБ	4

11С824Ф
Эксплуатация	1988...1996 гг.
Тип РН	«Протон-К»
Количество запусков	3
Отказы РБ	0
Аварии, не связанные с работой РБ	1

11С861-01
Эксплуатация	1982...2005 гг.
Тип РН	«Протон-К»
Количество запусков	13
Отказы РБ	0
Аварии, не связанные с работой РБ	0

17С40
Эксплуатация	с 1997 г.
Тип РН	«Протон-К»
Количество запусков	2
Отказы РБ	0
Аварии, не связанные с работой РБ	0

11С861-03
Летные испытания	с 2010 г.
Тип РН	«Протон-М»
Количество запусков	2
Отказы РБ	0
Аварии, не связанные с работой РБ	2

Коммерческие модификации разгонных блоков

ДМ1, ДМ2, ДМ3, ДМ4
Эксплуатация	1996...2006 гг.
Тип РН	«Протон-К»
Количество запусков	27
Отказы РБ	2

ДМ2
Эксплуатация	1997...2002 гг.
Тип РН	«Протон-К»
Количество запусков	4
Отказы РБ	0

ДМ- SL Б
Эксплуатация	с 1998 г.
Тип РН	«Зенит-3 SL Б»
Количество запусков	6
Отказы РБ	0

ДМ- SL
Эксплуатация	с 1999 г.
Тип РН	«Зенит-3 SL »
Количество запусков	36
Отказы РБ	0
Частично успешные пуски	1
Аварии, не связанные с работой РБ	3

Рис. 1. Статистические данные по результатам эксплуатации модификаций разгонных блоков типа Д и ДМ на май 2014 г.

Математическая модель для учета априорной информации о надежности при оценке ВБР изделия по результатам биномиальных испытаний

При оценке показателей надежности вновь разрабатываемых или модернизируемых технических объектов разработчик во многих случаях располагает некоторой информацией об этих показателях еще до начала испытаний. Она основывается на накопленном опыте создания подобных изделий, являющихся для проектируемого объекта прототипами. Информацию, имеющуюся до начала испытаний, называют априорной. Эта информация может быть представлена в виде совокупностей выборок результатов независимых испытаний изделий-аналогов, оценок числовых характеристик надежности или априорных распределений этих характеристик.

Задача заключается в том, чтобы за счет объединения априорной информации и экспериментальных данных вновь создаваемого или модернизируемого изделия получить достоверные оценки показателей надежности при минимальном количестве испытаний.

Для решения этой задачи могут использоваться различные методы математической статистики для оценки неизвестных параметров по экспериментальным данным, выбор которых определяется видом статистических данных по результатам испытаний и количеством наблюдений.

Сущность принятой математической модели для объединения информации состоит в следующем: допустим, имеется биномиальная статистика по результатам испытаний вновь созданной модификации изделия — n , d и изделия-прототипа — n ₁ , d ₁ , где n , n ₁ — количество испытанных образцов, а d и d ₁ — количество отказов.

В качестве нулевой статистической гипотезы принимаем предположение о том, что значения ВБР Р и Р ₁ обоих изделий одинаковы — Н ₀ : ( Р = Р ₁ ) при альтернативной гипотезе Н ₁ : ( Р ≠ Р ₁ ).

Если гипотеза Н ₀ справедлива, то точечная оценка вероятности безотказной работы изделия определяется по объединенной статистике: d + d

P_{H 0} 1     n ₊ n ₁ .

В противном случае

P = 1 – d .

H 1        n

В математической статистике в качестве критерия при проверке справедливости гипотезы Н ₀ используется уровень значимости, равный вероятности ошибки первого рода (принимается альтернативная гипотеза Н ₁ , когда справедлива нулевая гипотеза Н ₀ ).

Обычно для проверки нулевой гипотезы нужно задаться некоторым достаточно малым фиксированным значением уровня значимости α (например, α = 0,05...0,1), относительно которого строится критическая область Ω _α для наблюдаемой статистики Т ₀ .

Вместо того, чтобы назначать фиксированный уровень значимости α и только соглашаться с принятием или отклонением Н ₀ , можно использовать понятие «достигаемого уровня значимости» W , который при справедливой нулевой гипотезе определяется как вероятность получить отклонение большее, чем наблюдается, т. е. W = min {∝: Т ₀ ∈ Ω _α }.

При известном значении W точечная оценка ВБР новой модификации изделия с учетом прототипа может быть определена по формуле полной вероятности:

P_H         P_H .        (1)

Конкретное значение величины W определяется выбранным статистическим критерием для проверки гипотезы о принадлежности двух биномиальных выборок к одной генеральной совокупности.

Выбор критерия зависит от имеющегося количества наблюдений. Обычно количество ЛИ модифицированных изделий невелико, поэтому даже при большой статистике п результатов эксплуатации прототипов критерии, основанные на нормальной аппроксимации биномиального закона распределения, здесь не подходят. В связи с этим для решения поставленной задачи принимается критерий, предложенный в работе [1] для сравнения двух частот, основанный на биномиальном распределении. Применение этого критерия для решения задачи оценки

ВБР изделия по результатам разнородных испытаний обосновано в работе [2] и рекомендовано в виде расчетных соотношений в справочном пособии [3].

С учетом указанных предпосылок значение величины W определяется по формуле:

W = 2min{w, (1 – w)},(2)

min( d i + d, n i )

£ C Cd 1+d - r r = d 1 n 1 n                     ,    ,           ,    ,, где w =               , О , Cd^+d ~r и Cdv* d — бино-

Cd i + d         «1«1+« n i + n миальные коэффициенты.

Следует обратить внимание, что формула (2) позволяет получать нетривиальный результат, только если выборки по результатам испытаний содержат хотя бы один отказ.

Расчетные соотношения для оценки надежности вновь разработанной модификации РБ с учетом результатов эксплуатации прототипов

Рассмотрим возможность применения принятой математической модели для контроля за выполнением требований к надежности по результатам ЛИ новых модификаций РБ типа ДМ с учетом результатов эксплуатации прототипов на примере блока 11С861-03 первого этапа.

При оценке надежности вновь создаваемых модификаций РБ статистику по результатам эксплуатации РБ типа ДМ с учетом конструктивных особенностей и условий эксплуатации можно представить в виде трех подмножеств (таблица).

Статистические данные по результатам эксплуатации РБ

№ п/п	Модификации разгонных блоков (см. рис. 1)	РКН, в составе которых применялись разгонные блоки	Зачетная статистика*
			Запуски	Отказы или случаи неполного выполнения задачи
1	11С824М, 11С824Ф, 11С861, 11С861-01, 17С40, ДМ1–ДМ4	«Протон-К» или «Протон-М»	232	4
2	ДМ- SL	«Зенит-3 SL »	33	1**
3	ДМ- SL Б	«Зенит-3 SL Б»	6	0

Примечание. * Зачетными считаются все запуски разгонных блоков без учета случаев, когда причина аварий не была связана с работой блоков в автономном полете (отказы ракет-носителей, наземных систем, обеспечивающих подготовку к пуску, и проч.).

** Имеется в виду преждевременное окончание топлива при пуске РБ ДМ- SL № 11Л с космическим аппаратом Telstar -18 29.06.2004 г.

Непосредственное объединение статистики, полученной по результатам пусков ранее созданных модификаций РБ, и результатов ЛИ блока новой модификации для оценки его надежности правомерно, если они принадлежат одной генеральной совокупности, т. е. когда справедливо равенство Р = Р ₁ = Р ₂ = Р ₃ , где Р , Р ₁ , Р ₂ и Р ₃ — значения вероятностей безотказной работы новой модификации блока и, соответственно, его прототипов.

Применительно к случаю, когда нужно учитывать статистику по трем видам прототипов, соотношение (1) для определения точечной оценки ВБР нового изделия приобретает вид:

d d + d + d + d

= 1 – (q    + q 1    23

• ¹    n ² n + n ₁ + n ₂ + n ₃

d + d + d

+ q 12

• ³    n + n ₁ + n ₂

d + d + d

+q 23

• ⁵    n + n ₂ + n ₃

  + q ₄

  
  

  d + d + d

  1     3    +

  n + n ₁ + n ₃

  
  

  + q ₆

  
  

  d + d

  
  
  
  

  _{n + n}

  
  

  ^{1 +}

  
  

  d + d ₂

  
  

  + q

  ⁷ n + n ₁ + n ₂ + n

  
  

d + d ₃

+ q ), ₃      8 n + n ₃

где — точечная оценка вероятности безотказной работы по объединенной статистике; n и d — количество зачетных испытаний и отказов изделия новой модификации; n_i и d_i ∀ i = 1…3 — результаты испытаний соответствующих подмножеств прототипов; q_i ∀ i =1…8 — весовые коэффициенты, определяемые по формулам:

q ₁ = (1 – W ₁ )(1 – W ₂ )(1 – W ₃ )

q ₂ = W ₁ W ₂ W ₃

q ₃ = W ₁ W ₂ (1 – W ₃ )

q ₄ = W ₁ (1 – W ₂ ) W ₃

q ₅ = (1 – W ₁ ) W ₂ W ₃

q ₆ = W ₁ (1 – W ₂ )(1 – W ₃ )

q ₇ = (1 – W ₁ ) W ₂ (1 – W ₃ )

q ₈ = (1 – W ₁ )(1 – W ₂ ) W ₃

Гипотезы
Н 1,1	∧ Н 1,2	∧ Н 1,3
Н 0,1	∧ Н 0,2	∧ Н 0,3
Н 0,1	∧ Н 0,2	∧ Н 1,3
Н 0,1	∧ Н 1,2	∧ Н 0,3
Н 1,1	∧ Н 0,2	∧ Н 0,3
Н 0,1	∧ Н 1,2	∧ Н 1,3
Н 1,1	∧ Н 0,2	∧ Н 1,3
Н 1,1	∧ Н 1,2	∧ Н 0,3

W_i ∀ i = 1…3 — достигаемые значимости гипотез Н _{0 i} : ( Р = Р_i ) при альтернативе Н _{1 i} : ( Р ≠ Р_i ), ∀ i ^, = 1…3. ^,

Для оценки доверительных границ для ВБР вновь разработанной модификации РБ по объединенной статистике можно воспользоваться понятием эквивалентного количества испытаний [2], в котором испытания прототипа учитываются в виде относительной доли, пропорциональной соответствующему значению достижимого уровня значимости.

С учетом этого эквивалентная статистика определяется по формулам:

^{^} э = n t? ^ n ;          (4)

D _э = N_э (1 – ),             (5)

где N _э и D _э — эквивалентное количество испытаний и отказов блока новой модификации с учетом ре з ультатов эксплуатации прототипов, значение определяется по формуле (3).

В отличие от реальной биномиальной статистики, значения N _э и D _э могут принимать дробные значения, поэтому оценка нижней доверительной границы ВБР P _γ определяется как решение уравнения Клоппера-Пирсона [3] в следующем представлении:

I_P ( N э – D э ; D э +1) = 1 – γ, где I — неполная β -функция, P γ

P _γ

J t n ^{- r -} 1 (1 - 1 ) r dt

I ( n - r ; r + 1) = -----------------, где

P Y                      r

r — коли-

tn- r - 1(1 -1) rdt чество отказов. При целых n и r

r

I _n ( n - r ; r + 1) = CⁿP^{n - ;} (1 - P ) i .

P y                         i = 0 ¹ Y ^V Y⁷

Для численного решения уравнения (6) можно воспользоваться стандартной функцией БЕТАОБР программы Microsoft Excel .

В качестве численного примера применения формул (3–5) на рис. 2 приведен график зависимости оценки нижней доверительной границы ВБР при γ = 0,8 от количества безотказных ЛИ изделия с учетом данных по прототипам, приведенным в таблице. Для сравнения

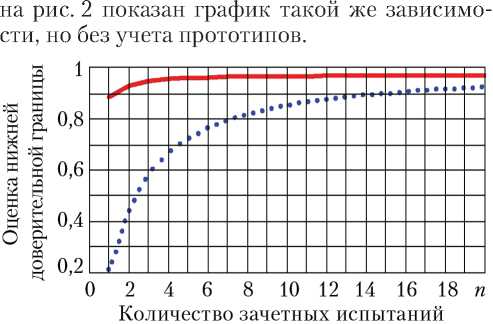
Рис. 2. Численный пример зависимостей подтвержденного уровня нижней доверительной границы вероятности безотказной работы новой модификации разгонного блока от количества безотказных летных испытаний при γ = 0,8 с учетом и без учета информации о результатах эксплуатации прототипов: – — с учетом результатов испытаний прототипов; . . . — без учета статистики по прототипам

Контроль за выполнением требований к надежности РБ по результатам летных испытаний

Как правило, количественное требование к надежности в полете отечественных средств выведения, включая РБ, устанавливается в форме нормативного значения ВБР Р _Н , которое должно подтверждаться испытаниями через контрольные уровни этого показателя с некоторой доверительной вероятностью γ .

Решение этой задачи может быть получено на основе стандартизированных методов статистического контроля качества продукции. Для контроля за соответствием изделия установленным требованиям к ВБР в ГОСТ Р27.403-2009 [4] предусматривается применение усеченных одноступенчатых и последовательных планов испытаний.

Летные испытания вновь разрабатываемых модификаций РБ типа ДМ осуществляются на фоне пусков прототипов. Количество пусков прототипов и их результаты сложно прогнозировать, поэтому для планирования количества ЛИ блоков с учетом данных по прототипам целесообразно использовать последовательный план, который не требует априори назначать необходимое количество испытываемых образцов. Положительной стороной последовательных планов испытаний является то, что их применение позволяет при прочих равных условиях на 40% уменьшать потребное количество испытываемых образцов по сравнению с одноступенчатыми планами.

Смысл последовательного плана состоит в том, что решение о соответствии изделия требованиям по надежности принимается, если сочетание значений эквивалентного количества испытаний и отказов — N _э и D _э — окажется в зоне приемки, в противном случае испытания продолжаются до попадания в зону приемки. При попадании значений N _э и D _э в зону браковки должно приниматься решение о доработке изделия (рис. 3).

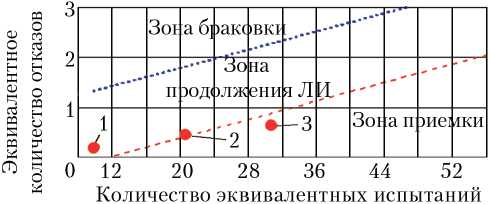
Рис. 3. Положение зон браковки, приемки и продолжения летных испытаний (ЛИ) для контроля за соответствием заданным требованиям вероятности безотказной работы при γ = 0,8; β = α = 0,2; Р _β = 0,9; Р _α = 0,985 Примечание. 1 — одно безотказное ЛИ; 2 — два безотказных ЛИ; 3 — три безотказных ЛИ.

Исходными данными для последовательного плана испытаний являются значения приемочного P _α и браковочного P _β уровней и значения рисков поставщика ( α ) и потребителя ( β ).

Риск поставщика — это вероятность ошибки первого рода, т. е. принятие решения о браковке изделий при условии, что истинное значение ВБР равно приемочному уровню. Традиционно обозначается так же, как уровень значимости при проверке статистических гипотез — α (см. выше).

Риск потребителя β — это ошибки второго рода, т. е. принятие решения о приемке изделий при условии, что истинное значение ВБР равно браковочному уровню P _β .

Границами указанных зон являются две наклонные прямые в системе координат N _э и D _э : D _э = aN _э + d ₀ — граница области браковки;

D _э = a ( N _э + n ₀ ) — граница области приемки.

Параметры a , d ₀ и n ₀ этих прямых зависят от принятых значений β , α , Р _β , Р _α и определяются по формулам, приведенным в ГОСТ Р27.403-2009 [4].

Значения рисков поставщика и заказчика α и β должны устанавливаться в согласованной методике, разрабатываемой в рамках реализации программы ЛИ изделия. В типовом случае в качестве приемочного уровня P _α принимается нормативное значение ВБР Р _Н , заданное в техническом задании. Значения рисков поставщика и заказчика привязываются к заданной в техническом задании доверительной вероятности так, чтобы β = α = 1 – γ .

Браковочный уровень Р _β можно определить из условия минимизации количества испытаний для плана однократной выборки, удовлетворяющего системе неравенств [5]:

• '    1 - I P ( N - R ; R + 1) C a

• '    I P ( N - R ; R + 1) C в ,         (7)

где N и R — количество испытываемых изделий и браковочное количество отказов для плана типа однократной выборки.

Например, если задано нормативное значение ВБР РБ в полете Р _Н > 0,985, то браковочный уровень, удовлетворяющий неравенствам (7) при R = 0, принимает значение Р _β ≈ 0,9.

На рис. 3 приведена диаграмма, иллюстрирующая положение зон браковки, приемки и продолжения испытаний для контроля за соответствием заданным требованиям ВБР при γ = 0,8; β = α = 0,2; Р _β = 0,9; Р _α = 0,985.

На эту же диаграмму нанесены точки с координатами N _э и D _э , определенными по формулам (4) и (5), при одном, двух и трех безотказных испытаниях нового изделия с учетом статистических данных по прототипам, приведенным в таблице.

Как следует из диаграммы на рис. 3, в рамках предпосылок, принятых для численного примера, требования к надежности функционирования РБ 11С861-03 могут считаться подтвержденными по результатам уже третьего успешного летного испытания.

Заключение

Рассмотренный в данной статье методический подход количественной оценки показателей надежности разгонных блоков с учетом априорной информации по результатам эксплуатации прототипов позволяет сократить количество летных испытаний для подтверждения заданных требований к вероятности безотказной работы в полете.

Использование последовательного плана для контроля вероятности безотказной работы по результатам летных испытаний позволяет учитывать результаты эксплуатации прототипов в условиях, когда летные испытания новой модификации изделия проходят на фоне эксплуатации прототипов. Кроме того, при равных исходных предпосылках последовательные планы испытаний требуют меньшего количества образцов, необходимых для испытаний, по сравнению с однократной выборкой, когда количество образцов назначается заранее.

Данный методический подход может представлять интерес и для других видов изделий, где новые образцы создаются как модификации отработанных прототипов с сохранением общих принципов обеспечения надежности и контроля качества при изготовлении.