Погрешность цифрового вольтметра переменного тока, обусловленная квантованием по уровню

Одной из подзадач при проектировании цифрового вольтметра переменного напряжения является оценка погрешности, обусловленной квантованием по уровню. Данное значение позволяет определить минимальное требуемое количество разрядов АЦП. При этом оценка этой погрешности необходима с учетом метода измерения. Для того чтобы оценка учитывала функцию преобразования измеряемого сигнала, надо привести погрешность к показаниям вольтметра.

Задача измерения действующего значения сводится к нахождению среднего значения квадрата сигнала.

На данный момент хорошо развита методика вероятностного оценивания погрешности квантования [1–9], но она не всегда применима и позволяет получить исключительно завышенную оценку в условиях пренебрежимо малых шумов на входе. Также одна из сложностей получения такой оценки – это нелинейная функция преобразования звеньев, обрабатывающих квантованный сигнал. Так, в статьях [8, 10] и более ранней [11] были оп-

ределены погрешности квантования при равномерном шаге квантования и линейной функции преобразования. Полученные результаты были дополнены в ряде статей [12–15] и подытожены в статье Элиаса в 1970 г. [16]. Обширное описание истории развития области исследования квантования представлено в работе [17].

При этом погрешность квантования сигнала можно разделить на погрешность квантования по времени и погрешность квантования по уровню [18]. В данной статье получены математические модели, позволяющие оценить погрешность квантования по уровню для цифрового вольтметра действующего значения. Таким образом, при моделировании можно оценить погрешность, обусловленную квантованием по уровню при использовании цифрового вольтметра, чей принцип работы показан на рис. 1, и выбрать допустимую разрядность.

В данной статье получена модель погрешности квантования по уровню цифрового вольтметра, показанного на рис. 1. Модель апробирована в среде SciLab [19].

Волович Г.И., Литвинова Е.В., Мунтьянов С.Н., Яковлев В.А.

Рис. 1. Упрощенная блок-схема цифрового вольтметра

Модель АЦП

Рассмотрим синусоидальный сигнал на входе вольтметра:

y(t) = Л • sin(w • t + ф), здесь to - круговая частота сигнала; ф - фаза сигнала; А - амплитудное значение напряжения.

Число квантов, которые полностью перекрывают сигнал, определится как

Зависимость выходного сигнала АЦП y от входного сигнала x [20] будет определяться как

у = й

Рассмотрим первый полупериод с нулевой фазой φ .

Дискретный сигнал на первой четверти периода будет принимать значения при n = 1… N :

Д • и = Л • sin(to • т1л + ф)

или

и • ^ = sin(to • т^ + ф).

Время, когда на выходе происходит изменение сигнала на одну дискрету вверх: arcsin(n- r )

Чп=—Щ^.                                                   (1)

Время изменения сигнала скачком на одну дискрету вниз:

^-arcsinfn- r )

Чп =----.                                                                             (2)

Дискретный сигнал на второй четверти периода будет принимать значения при n = 1… N :

Д • (и - 1) = Л • sin(to • т3,„ + ф)

или

(и - 1) • Д = sin(to • т3,„ + ф)

в соответствующие моменты времени т₃ ,„ .

Рассмотрим второй полупериод с нулевой фазой φ .

Время, когда на выходе происходит изменение сигнала на одну дискрету вверх:

„^О.-.^(3)

3,п шш

Время изменения сигнала скачком на одну дискрету вниз:

+ .-„in((„-1>.A).(4)

• *,u шш

Тогда модель сигнала на выходе АЦП можно описать следующим выражением, n = 1, 2, 3…

• У * (к • Ts) = Д (z^ i 1 (к • Ts - т_и + ^ - 5 'Ll 1 (к • Ts - т_2Д -'J-

• + Z"?1(k^s-T3,i+^)-Z^11(k^^

Квадратор

Квадрат полученного дискретного сигнала (6):

(y*(kTs))2 = Д2 • (I'Ll 1(kTs - ri,z) - I'Ll 1(kTs - T2,0)2.

Распишем данное выражение:

■ ■ ■ (V.v Hk VT< . .)) +(Z'=i1(k^Ts-T2^) -

-2 • 5'Ll 1(k • Ts - T1.,) • 5'Ll 1(k • Ts - T2,i).

Момент r2 > rl, следовательно , e ,            2

■ ' ' ;vy Hk-Ts  . .)) +(5'Ll1(k^Ts-T2,)) -2^5'Ll1(k^Ts-r2^).

Воспользуемся в дальнейшем тем, что

(5'Ll 1(kTs - Tl,y))2 = 5'li(2 •; - 1) • 1(kTs - Tl,y).

Устройства аналоговой и цифровой электроники

П ри у чете то го, что ква н то в анный сигнал принимает значения, симметричные относи т е ль но п и ков о го зн ачения, а т₂ нас т у п ает позд не е д ос т ижения сигналом пика, и учитывая аналогичные выв о д ы для т₄, справедливо:

(у * (к • Ts))² = Д ² X ” ₌ 1 (± 7=1 (2 •; - 1) • (1 (kTs - _Чу + ^) - 1 (kTs - T 2j + ^)) +

+ \ Z' ⁽² j - 1) • (1 (^kTs - _Чу + ^) - ¹ (^kTs - T 4j + ²= ))).                               (6)

Среднее значение за период сигнала

Найдем постоянную составляющую сигнала на выходе квадратора. Частота дискретизации кратна частоте сигнала. Для упрощения расчётов будем рассматривать отношение квадрата дискретного сигнала к квадрату шага квантования:

(y_z) ² = - (4^) = £ 7=1 (2 x - 1) •         + X;' * 1 (2 •; -1) •     .'                             (7)

После подстановки (1)–( 4) в (7):

arcsinf (n> 4 )                         arcsinf (n-1)- 4 )

(y_z) = 2 • ^ ² + 2^ + 1 - S 7 ₌₁(2 • И - 1) •      2 Д - X 7*1 (2 • n - 1) •      ----.

Данное выражение показывает выходной сигнал идеального фильтра как функцию от N, где N – ок- ругленное значение отношения амплитуды к шагу квантования.

Тогд а о т нос ите л ьн ая ош и б ка , в ыз в а нная кв антов ан ие м по уров ню:

„           ar c s in (n.A)                arcsin((n-l).A)\

72 -X"=1 (2 ^n-1)--_£W+l (2 -n-1)--Z_-----1_л error =

A

Данная погрешность имеет точки экстремума для каждого N. Соответственно максимальная из них и является искомой погрешностью.

Мини мумы б у д у т нах од ить с я в особых точках, а для нахождения максимума на й д е м произ в одн у ю по ошибке и приравняем её к нулю. Реш е ни е данного уравнения даст необходимое значение аргумента ошибки.

Д а нн ы е в ыра ж е н ия нел и нейные . Та ким обра з ом , получе ние ана лит иче с ко го выражения трудоёмко. В ос пол ьзуе м с я м е тодом по л ов и нного деления для нахождения корней полученны х в ыра ж ен ий. Р е зу л ьт аты, полученные в Scilab , п ре д с тавл е ны в в и де гра фика н а рис . 2.

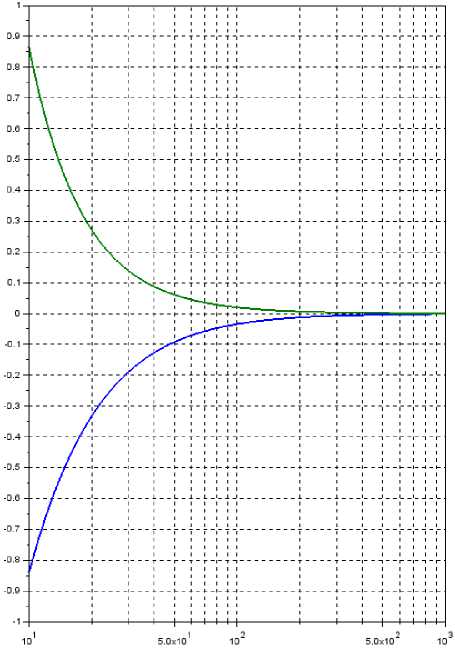
Рис. 2. Зависимость относительной погрешности, %, от отношения амплитуды к шагу квантования

Волович Г.И., Литвинова Е.В., Мунтьянов С.Н., Яковлев В.А.

На рис. 2 видно, что погрешность квантования определяется отношением минимальной амплитуды сигнала, которую необходимо измерять, к шагу квантования.

Аппроксимация данной зависимости методом наименьших квадратов от N = 2 до 1000 с максимальной относительной погрешностью аппроксимации, не превышающей 2,8 %, представлена ниже:

-eC3,4341-^^ • (n - 0,08)"1,47594 < 5 << е^^Т^Ы • (n + 0,4816)"1,5042, где 5 - относительная погрешность измерения в процентах.

Тогда соответственно относительная погрешность может быть оценена как

5 « 100 • max^ ^-1,171-^^ • (N - 0,08) ^-1,⁴⁷⁵⁹⁴_e^(-1,7471+v^^ • (n + 0Д816) -¹,⁵⁰⁴² ).

Цифровой фильтр нижних частот

Для использования неидеального фильтра рассмотрим сигнал, получаемый на выходе квадратора (6).

Сигнал (6), представленный в форме ряда Фурье:

(у*№)) ² = Д ² 5 7=1 — + Д ² 577 — + 2Д ² • 5 „ =1 (5 7=1 sinc (—) • — • cos(w • и • kTs) + ^S1J              ^S2J                  \            Vlj/ ^S1J

+ 5 7=7 sinc ( s^ ) • yT^-1 • cos(w • и • kTs + л • и)), где s_k j - скважность, определяемая следующим образом: _ т _

• ^{5 1,7} “ ^T2j^-TV т

  ^{5 2,7    Т} 4,~ ^Т 3,/

  Для учета квантования по времени при частоте дискретизации, кратной частоте сигнала, s_k j заменится

  
  

на 5~_а, где s~ , определяется как:

_       т

• ⁵¹⁷ ~ [^⁺4^тН^⁺4^тх ;

_       т

• ^52,7 ~ ^[ ^⁴^ ⁺¹]^^тх-[ 1^^ ⁺¹]^^тх .

Для фильтра высокого порядка при соблюдении условия о кратности частоты дискретизации и частоты сигнала и частоте среза ниже частоты сигнала для k много больше постоянной времени фильтра справедливо

• У /² -Д ² 5 7=1;~- + Д ² 5 7=⁺1¹;г ^.                                                                    (11)

¹,j                          ^Z,J

При несоблюдении данных условий квадрат дискретизированного сигнала можно представить как

(y * (k • Ts)) ² = Д ² 5 ” =1 (5 7=1 (2 • J - 1) • (1 (f^(kTs)) - 1 (f^(kTs))) +

+ 5 7=7 (2 •; - 1) • (1(4 7,; (kTs)) - 1(f4^(kTs)))),                                           (12)

где

Krs-Ti^—

T~_n(kTs) = [---- .    ■■ . i^Ts

Тогда на выходе ФНЧ yp(kTs) = Д2 5n=1 (57=1(2 •; - 1) • (^ (47(kTs)) - h (^(kTs))) +

+ 5 7=7 (2 •; - 1) • (h (7 (kTs)) - h (7(kTs)))),                                      (13)

где h ( t ) – переходная характеристика фильтра.

Соответственно, на выходе будет наблюдаться величина yf(kTs) = Jy/(kTs).                                                                        (14)

Так, для сигнала, представленного в примере 3 статьи [4], подставив (11) в (14), получаем 2,96∙10–5, что соответствует результатам моделирования.

При моделировании по формуле (14) при соблюдении соответствующих условий для определения фильтрованного квадрата дискретизированного сигнала, разность между прямым методом моделирования и полученным моделям была равна нулю.

Устройства аналоговой и цифровой электроники

Выводы

Получены зависимости погрешности цифрового вольтметра в зависимости от квантования по уровню. Результаты представлены на рис. 2. Зависимости аппроксимированы с погрешностью, не превышающей 2,8 % на интервале отношения амплитуды сигнала к шагу квантования от 2 до 1000, зависимостью (9).

Получена аналитическая модель дискретизированного сигнала на выходе АЦП, представленная выражением (5), и квадрата этого сигнала, представленного выражением (6) и (10).

При использовании цифрового фильтра нижних частот важной особенностью можно выделить влияние частоты квантования на погрешность при соблюдении зависимости (9).

Получены аналитические модели погрешности квантования по уровню, приведенные к выходу цифрового вольтметра, для идеального фильтра низких частот. Найденные выражения позволяют определить минимально допустимый шаг квантования АЦП или ЦАП для известного допустимого уровня погрешности и минимальной амплитуды входного сигнала, без учета квантования по времени и шума в измеряемом сигнале, при условии использования метода измерения, представленного на рис. 1.

Модели, позволяющие оценить погрешность квантования по уровню, апробированы в среде программирования Scilab.