Погрешность определения напряжённо-деформированного состояния режущего инструмента

При проектировании конструкции и технологии изготовления режущих инструментов на этапе прочностного расчёта, расчёта погрешности обработки и выполнения других задач, важным является достоверное определение напряжённо-деформированного состояния (НДС). Для этого применяются методики сопромата, методы конечно-элементного анализа, эмпирические, феноменологические и пр. При этом используются различные по своей сложности схемы нагружения с различной степенью приближения к реальным условиям. Понятно, что большее приближение даёт большую достоверность, но при этом увеличиваются и затраты: временные и финансовые, связанные с наличием соответствующей аппаратуры и квалификации исследователя. И здесь встаёт вопрос о рациональности использования тех или иных методик для достижения поставленной перед исследователем цели. Должен быть выбор между ценой и качеством определения НДС.

Целью данной работы является определение относительной погрешности расчёта НДС токарного расточного резца при использовании аналитических моделей сопротивления материалов и метода конечных элементов с различной степенью приближения к реальным условиям.

тангенциальная составляющая P_z, приводящая к изгибу резца .

Самым простым вариантом для определения действующих напряжений является использование плоской модели, в которой резец представляется как балка с защемлённым концом с вылетом l , испытывающая изгибающие нагрузки от тангенциальной составляющей P_z , действующей на главную режущую кромку (см. рис. 1) [1].

Напряжения на изгиб определяются, как:

аи=^,Па,        (1)

где М _изг – изгибающий момент, действующий на резец в зоне крепления резца в резцедержателе станка; W – момент сопротивления резания при изгибе.

M,, = p,i,HM,

_ Tr DS                                n w =--- – для круглого сечения, где D – ди- аметр державки, м.

Подставим их в первую формулу и получим: - для резцов с прямоугольным сечением:

;

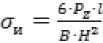
- для резцов с круглым сечением:

.

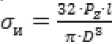
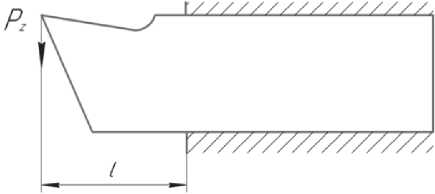
Рис. 1. Схема для расчёта напряжений резца при использовании плоской модели

Тангенциальную составляющую силы резания P_z можно приближённо определить по формуле:

P_z = 10-k - F, Н,          (4)

где k – коэффициент резания, зависящий от свойств обрабатываемого материала; F– пло- щадь поперечного сечения стружки, зависящая от подачи s (мм/об) и глубины резания t (мм): F = t.s, мм2.

Приведённый расчёт на плоский изгиб – простой, но неточный, так как на резец действу- ют также осевая и радиальная составляющие силы резания Рх и Ру, создающие дополнительные нагрузки на изгиб, кручение и сжатие. В результате такого сложного сопротивления, напряжения резца увеличиваются, по мнению авторов [2], в зависимости от величины углов в плане, примерно в два раза. Кроме того, данная схема предполагает, что наиболее опасным яв- ляется сечение державки, отстоящее от вершины резца на расстоянии вылета l. В некоторых конструкциях может оказаться, что наиболее слабым является головка резца в месте выреза под пластину.

Для резцов с малым сечением среза и большим вылетом (отрезных, расточных) производится также проверка на жёсткость. Здесь стрела прогиба f (см. рис. 2) находится, как [2]:

P !a f =    , м,             (5)

где Е – модуль упругости материала державки резца ((200...220) ^. 10⁹ Па); I – момент инерции державки:

т ^B^ 4

• -    для прямоугольного сечения Z =     , м ;

• -    для круглого сечения I = ---- , M.

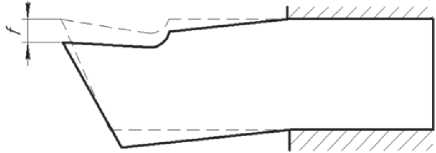
Рис. 2. Схема для расчёта прогиба резца при использовании плоской модели

Более достоверным способом расчёта НДС является метод конечных элементов. Но здесь требуется наличие соответствующей квалификации исследователя, автоматизированное рабочее место с программным обеспечением, 3D-модель исследуемого изделия. Однако и тут погрешность расчёта зависит от множества факторов: типа конечных элементов, параметров сетки, контактных параметров и пр.

Наиболее простой вариант - отыскать на сайтах производителей модель требуемого инструмента и подвергнуть её расчёту. Про- блема заключается в том, что модель создана, как правило, упрощённо, с низкой детализацией. Например, на рисунке 3, в сечении расточного резца S25T-CTFPR видно, что рычаг крепления 2 режущей пластины 3 к корпусу 1 не имеет отверстия под винт, отсутствует сам винт крепления, обязательный для данной конструкции. По сути, конструкция является монолитной. Всё это, безусловно, должно сказаться на погрешности расчёта НДС, вопрос только – в какой степени.

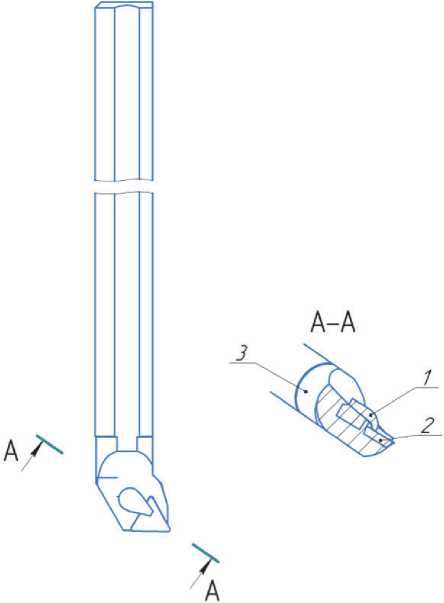
Рис. 3. Эскиз модели расточного резца S25T-CTFPR с сайта производителя [3]:

1 – корпус; 2 – рычаг крепления;

3 – режущая пластина

Ещё один вариант – это расчёт напряжённо-деформированного состояния сборной 3D-модели с полной детализацией, включающей металлорежущую пластину, элементы её крепления и необходимые пазы, канавки и отверстия. Здесь погрешности расчёта сведены к минимуму, однако такой подход является наиболее трудоёмким.

МЕТОДИКА ИССЛЕДОВАНИЙ

Для определения погрешности расчёта НДС токарного расточного резца использовалось три подхода: использование плоской модели расчёта резца по формулам сопромата, монолитная 3D-модель – методом конечных элементов и подробная 3D-модель – также методом конечных элементов. За эталон, относительно которо- го рассчитывалась относительная погрешность, принимался последний метод.

Расчёт 3D-модели токарного расточного резца производился в модуле прочностного конечно-элементного экспресс-анализа APM FEM по рекомендациям авторов [4, 5].

Исходные данные. Расточной резец S16M-PCLNR 09. Подача s=0,3 мм/об; глубина резания t=3 мм, коэффициент резания k=164, Вылет вершины резца l=75мм. Диаметр державки D=16 мм.

Тангенциальная составляющая силы резания, по ф.4, составила P _z ≈1500 Н. Напряжения и деформации для первого варианта определялись по формулам 3 и 5; результаты занесены в таблицу.

Параметры сетки конечных элементов использовались следующие [5]:

• 1.    Десятиузловые тетраэдры (использование 10-узловых тетраэдров позволяет использовать больший шаг разбиения по сравнению с 4-узло-выми, что экономит память и ресурсы компьютера при обеспечении точности расчёта).

• 2.    Максимальная длина стороны элемента 2 мм (величина, характеризующая размер конечного элемента (тетраэдра)).

• 3.    Максимальный коэффициент сгущения на поверхности 2 (определяет, насколько следующий элемент можно сделать (где необходимо) меньше).

• 4.    Коэффициент разрежения в объеме 1,5 (степень увеличения стороны тетраэдра при генерации сетки вглубь объема твердотельной модели).

Тип расчёта – статический.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В результате расчёта НДС, приведённого в таблице и на рисунках 4 и 5, получили следующее.

По методике сопромата погрешность расчёта изгибающих напряжений относительно эталона составила 30%; их величина оказалась сильно заниженной. При использовании этого подхода в конструировании рекомендуется использовать коэффициент запаса прочности не менее трёх, что, конечно же, приведёт к менее эффективному коэффициенту использования материала, но сохранит надёжность. А вот величина прогиба (деформации) вершины резца оказалась практически идентичной эталону.

При использовании монолитной 3D-модели погрешность расчёта изгибающих напряжений, относительно эталона, составила 21%; их величина, наоборот, оказалась завышенной и коэффициент запаса здесь рекомендуется брать равным единице. Относительная погрешность деформаций в данном случае составила 33% и также оказалась завышенной. Причины такого расхождения пока не ясны.

Если внимательно посмотреть на рисунок 5, то можно увидеть, что максимальная величина напряжений при расчёте сборной 3D-модели находится не в месте крепления державки резца, а в месте крепления сменной режущей пластины (СМП) и сильно отличается в большую сторону (3331 МПа по сравнению с 280 МПа и 1141 МПа). Этот факт говорит о том, что плоская модель сопромата и метод конечных элементов с монолитной 3D-моделью не адекватно оценивают напряжения в целом для сборного инстру-

Таблица. Результаты исследования погрешности определения НДС

Определяемый параметр	Плоская модель	Монолитная 3D-модель	Сборная 3D-модель
Напряжение а и , МПа	280	1141	940
Деформация f , мм	0,328	0,435	0,327
Абсолютная погрешность напряжения С и , МПа	660	201	0
Абсолютная погрешность деформации, мм	0,001	0,108	0
Относительная погрешность напряжения С и , %	30	21	0
Относительная погрешность деформации, 5, %	0,3	33	0

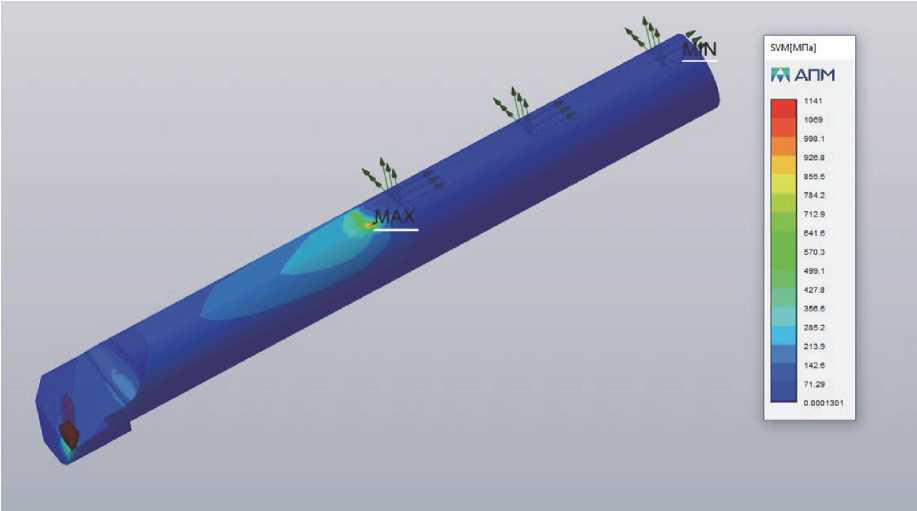
Рис. 4. Результаты расчёта напряжений монолитной 3D-модели

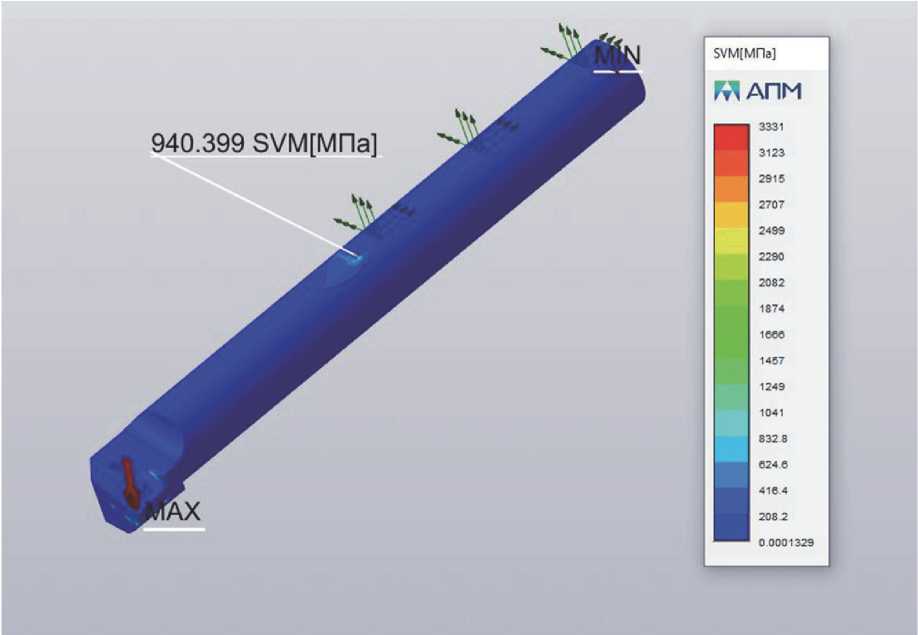
Рис. 5. Результаты расчёта напряжений сборной 3D-модели

мента с СМП и годятся только для цельных или составных конструкций резцов.

ВЫВОДЫ

• 1.    При использовании плоской модели сопромата для расчёта изгибающих напряжений в державке резца рекомендуется принимать коэффициент запаса не менее трёх. Прогиб вер-

• шины резца под действием тангенциальной составляющей силы резания данная модель определяет адекватно.

• 2.    При использовании метода конечных элементов с упрощённой (монолитной) 3D-моделью напряжения получаются немного завышенными, и коэффициент запаса рекомендуется брать равным единице. Погрешность величины прогиба резца также завышена.

• 3.    Для расчёта статических напряжений от сил резания инструмента со сменными многогранными пластинами рекомендуется использовать метод конечных элементов с подробной 3D-моделью, поскольку максимальные напряжения могут возникать не в месте крепления державки в станке, а в месте крепления СМП.