Point defects in nematic liquid crystal materials with conical anchoring at the interface

Introduction. Liquid crystals (LC) are anisotropic liquids with long-range orientational order of molecules. The orientation of LC molecules is characterized by the director n , which is a unit vector oriented along the preferred orientation of the long axes of the molecules [1]. A rich variety of forming configurations of the director's field is possible in an LC, depending on the boundary conditions (preferred orientation of the director at the interface), material parameters of the LC (elasticity constants, helix pitch), external electric or magnetic fields [2]. In this case, defects can be formed in the system, where significant distortions of the director field are observed. And vice versa, upon induction of strong distortions in the volume, for example, by magnetic (electric) fields or introduction of microparticles into the LC, topological defects are formed. The resulting distortions of the director field facilitate interaction between defects and particles which can be found in the effects of selfordering of defects [3–5], colloidal [6; 7] and magnetic [8] particles, makes it possible to control the position of microparticles [9], and determines the group motion of defects in external electric field [10]. Thus, topological defects are an important feature that significantly affects the main characteristics of liquid crystal materials (optical, electro-optical, dynamic) which determine their prospects for various applications in modern information technologies.

Point bulk (hedgehogs) [11; 12] and surface (boo-jums) [13] defects, linear defects [14] and twodimensional defects (walls) [2] can be formed in nematic LC. In the case of twisted nematic with the ratio d / p ≈ 1 of the layer thickness d and the helix pitch p , soliton-like structures [15] or linear defects [16] can be formed in the system. The possibility of formation and stability of various types of defects is determined by the boundary conditions specified on the substrates. Thus, under degenerate tangential (planar) boundary conditions (the angle between the director and the normal to the surface is 90°), a schlieren texture is formed in the LC cell which consists of point and linear defects, the strength of which depends on the ratio of the LC elastic constants [17]. In the case of homeotropic anchoring (the angle between the director and the normal to the surface is 0°), there are initially no defects in the system, but the application of an electric field or a combination of electric and magnetic fields promote the formation of an ordered set of point defects [3], two-dimensional defects [2], or soliton-like structures in twisted nematic [15]. Under homeo-planar boundary conditions, the formation of point defects on a substrate with planar anchoring or a structure of domains with closed linear defects is possible in the system.

Conical boundary conditions (the director is oriented to the surface normal at an angle other than 0° and 90°) are more suitable for the occurrence of defects. For example, in a cell with a conical anchoring, point, linear, and two-dimensional defects are formed even when there are no external fields [18]. In the case of a twisted nematic with planar-conical anchoring, linear defects are formed [19] or domains bounded by a closed linear defect with a pair of point singularities [20]. At the same time, point defects in LC systems with conical anchoring have not been practically investigated to this date.

This work presents for the first time the results of studying the structures of point defects formed in nematic and twisted nematic under conical boundary conditions on both substrates.

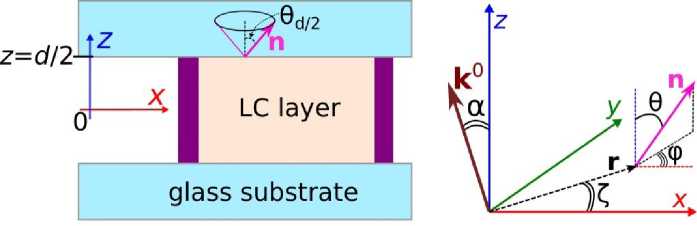
Materials and methods. The studies were carried out for a nematic LN-396 mixture (Belarusian State Technological University) and LN-396 mixture doped with a lefthanded chiral addition of cholesteryl acetate (Sigma Aldrich). The concentration of cholesteryl acetate was 0.2 % which determines the pitch of the cholesteric helix with a value of p = 72.5 μm [19]. The studies were carried out in LC cells consisting of two glass substrates assembled in such a way that a gap is formed between them which is filled with a liquid crystal (fig. 1, a ). Glass substrates were coated by centrifugation with a poly(isobutyl methacrylate) film (Sigma Aldrich) which sets conical boundary conditions for the used nematic LN-396 with a polar angle 6 d _/2 = 40 ° [21]. The thickness d of the LC layer was set with glass balls and was measured by the interference method until the cell was filled with a liquid crystal. LC cells were filled at room temperature and kept for at least 24 hours before to the study. The studies were carried out using a polarizing microscope (POM) AxioImager.M1m (CarlZeiss) with a 20x / 0.22 long-focus objective in monochromatic light with a wavelength of λ = 546 nm. The refractive indices of LC LN-396 n _± = 1.528, n । = 1.741 (X = 546 nm).

Oblique incidence light method. It is convenient to describe the distribution of the director field in the cell using the polar θ ( x , y , z ) and azimuthal φ ( x , y , z ) angles (fig. 1, b ). In this case, the n -director is described by the following equation:

n x = ^sin H x , У , z ] ) ^cos ( ф [ x , У , z ] ) , <  n y = sin ( 9 [ x , y , z ] ) sin ( ф [ x , y , z ] ) ,          (1)

n z = cos ( 9 [ x , y , z ] ) .

Generally, the angles θ and φ can vary both over the thickness of the LC layer and in the plane of substrates.

This is more typical for the LC areas near defects, and the nature of the change in the angles is determined by the type of defect. Conversely, the nature of the change in the angles in the vicinity of the defect can be used to determine its parameters. In the case of point defects in nematics, the method of fluorescence microscopy is used [22]. In the case of an tilted orientation of the director in the bulk which is realized under conical boundary conditions, it is convenient to use the method of oblique incidence of light proposed and described below in order to characterize defects.

Consider a twisted nematic away from defects. In this case, we can assume that the polar angle of the director is constant and equal to the tilt angle of the director on substrates θ ( x , y , z ) = θ d / = θ –d / , and the azimuthal angle φ ( x , y ) depends on the coordinate z linearly:

ф ( x , y , z ) = Ф о ( x , y^^dA. z , (2)

where φ₀( x , y ) – azimuthal angle of the director at the center of the layer (at z = 0), φ_TOTAL is the difference between the azimuthal angles of the director on the upper ( z = +d/ 2) and lower ( z = –d /2) substrates (the total azimuthal angle of rotation of the director on the layer d -thickness). Consider the oblique incidence of the light beam on the LC layer in the xOz plane (fig. 1, b ). The direction of the beam will be characterized by the unit vector k ⁰(±sinα, 0, cosα), where the plus sign corresponds to the zero azimuthal angle for the vector k ⁰, the minus sign corresponds to the value of the azimuthal angle of the vector k ⁰ equal to π. When Mauguin condition [23] is fulfilled, we can assume that two linear waves propagate in such a twisted structure, the phase difference between which in the case of oblique light incidence at an angle α is determined as:

) dz ‘ - n ₂

5 =

r„, 2 n d    r           n i n

^X cos ^a - 12 n 2 + ( n 2 _ n 2 ) cos² ( Q‘ )

, (3)

where z ’ = z / d , cos(θ’) equals:

cos ( 6' ) = nk ⁰ =± sin a sin I 9 _{d /} I cos ( ф ₀ ( x, y ) + Ф _TOTAL z ‘ ) +

+ cos a cos I 9 d/

X /2

Fig. 2 shows the dependences on the angle φ 0 ( x , y ) of the δ/ d values calculated by equation (3) for several values of the total twist angle φ TOTAL at an oblique incidence at an angle α = 5.33° (for the case shown in fig. 1, b ), and polar angle θ d /2 = 40°. It can be seen that one maximum is observed in the dependences only at the angle φ 0 ( x , y ) = 0°, and an increase in the angle φ TOTAL leads to a slight decrease in the difference (δ max – δ min )/ d from a value of approximately 0.43 rad/μm to 0.27 rad/μm for angles φ_TOTAL 0° and 180 °, respectively. Such a difference in the phase differences observed for different azimuthal angles φ 0 ( x , y ) can be easily fixed for the commonly used LC cell thicknesses of about 10 μm. At the same time, the angle α used for calculation makes it easy to carry out observations with a polarizing microscope using a long-focus lens. The data presented in fig. 2 were obtained for positive angles φ TOTAL (righthanded cholesteric), while due to the symmetry of the structure relative to the center of the layer, identical results are obtained for negative angles φ_TOTAL (lefthanded cholesteric).

The above results were obtained from the assumption that the polar angle of the θ-director is constant and there is a simple linear dependence of the azimuthal angle φ on the coordinate z . In general, these conditions may not be met. For example, in a twisted nematic structure with significant pretilt angles of the director on substrates, the polar angle θ begins to depend on the z coordinate, while the dependence of the azimuthal angle of the director on the z coordinate deviates from the linear law [24]. Nevertheless, the results obtained for simple cases show that the maximum value of δ is reached at φ₀( x , y ) = 0° regardless of the values of the angle θ _{d /2} and φ_TOTAL.

b

a

Fig. 1. Scheme of LC cell ( a ) and the coordinate system used to calculate the optical phase difference at oblique light incidence and the director field around the boojums ( b )

Рис. 1. Схематическое представление ЖК ячейки ( a ) и система координат, используемая для расчетов оптической разности фаз в случае наклонного падения света и поля директора вокруг буджумов ( b )

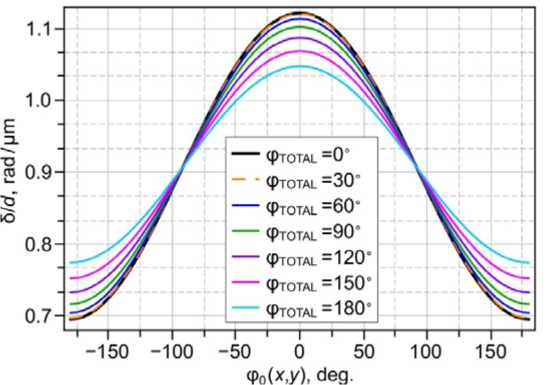
Fig. 2. Dependences of the ratio δ/ d on the angle φ 0 ( x , y ) calculated for some twist angles φ_TOTAL. The data have been calculated for the angles α = 5.33°, θ( x , y , z ) = θ _{d /2} = 40°, the wavelength λ = 546 nm and the refractive indices corresponding to LC LN-396

Рис. 2. Зависимости отношения δ/ d от угла φ₀( x , y ), рассчитанные для нескольких углов закрутки φ_TOTAL. Расчет сделан для углов α = 5,33°, θ( x , y , z ) = θ _{d /2} = 40°, длины волны света λ = 546 нм и показателей преломления, соответствующих ЖК ЛН-396

Thus, this conclusion can be extended to the case of an inhomogeneous slope and an uneven twist angle in the case when the director distribution in the bulk is symmetric about the center of the layer. It is this situation that is realized in LC cells under the same boundary conditions in the absence of external influences (for example, an electric field). Further, this method will be applied to analyze boojums that form in nematic and twisted nematic under conical boundary conditions.

Boojums in nematic. In the absence of a given orientation of the director on the substrates (degenerate tangential or conical boundary conditions), point defects on the surface (boojums) are formed in the system. Near boojums, the orientation of the director on the surface (plane z = d /2) can be described as [25]