Поиск главных минимумов многоэкстремальных функций при активном учёте ограничений неравенств

При получении (изучении) законов природы и конструировании объектов применимы экстремальные принципы. При этом формулируется экстремальная задача (например, минимизации функции или функционала в допустимой области изменения варьируемых переменных; мы в дальнейшем рассматриваем только минимизацию функций) и находится её решение, например, глобальный минимум функции. Качество получаемого решения, как правило, определяется величиной минимизируемой функции; тогда под подозрение надо ставить не только точку глобального минимума, но и точки близлежащих (по величине минимизируемой функции) минимумов. При конструировании объектов эти точки могут соответствовать более эффективным вариантам за счёт многокритериального оценивания их эффективности. Глобальный и близлежащие к нему минимумы будем называть главными минимумами.

В работе [1] предложен алгоритм поиска главных минимумов при изменении независимых переменных в гиперпрямоугольной области. Фрагменты решения на основе его простейших численных примеров приведены в [2, с. 139–143]. Примеры демонстрируют хорошее качество работы алгоритма – высокое быстродействие и точность.

В реальных условиях допустимая область поиска (определяемая, как правило, ограничениями типа неравенств) может быть сколь угодно сложной и достаточно узкой (в виде жгута).

Проблеме учёта этих ограничений при поиске главных минимумов посвящена предлагаемая работа. При этом, естественно, мы переносим опыт работы с ограничениями, полученный при конструировании алгоритмов поиска одного глобального минимума [2], на решение задачи поиска главных минимумов многоэкстремальных функций.

Постановка задачи

Необходимо отыскать заданное количество главных экстремумов функции многих переменных

I ( х ) = гл min, х = ( X i ,..., X m ) .                                         (1)

X E X

Допустимая область X определяется системой ограничений неравенств

^{9 j ( X} ) < ^{0, j 1 m} * "                                                  ⁽²⁾

Ограничения сужают область поиска экстремума. Функция качества I ( х) может быть многоэкстремальной, разрывной, недифференцируемой, а также может быть искажена помехой. Функции ограничений тоже могут быть невыпуклыми и недифференцируемыми. Поиск экстремумов осуществляется только на основе измерений или вычислений указанных функций: —

I ( X ); j X ), j = 1, m i .

Алгоритмы

Все приводимые ниже алгоритмы поиска включают в себя два этапа: первый этап – это разбиение исходной области на подобласти, второй – поиск глобального минимума в каждой из найденных подобластей.

Исследователь задает: 1) исходную гиперпрямоугольную область П⁰ (с центром в х ⁰ и интервалами А х ⁰), которая должна содержать в себе искомые главные экстремумы; 2) количество исходных пробных точек n ⁰, равномерно распределённых внутри этой области; 3) количество главных минимумов n _{гл мин}; 4) количество пробных точек n , вид ядра и степень 5 его селективности, используемые при поиске глобального минимума в каждой подобласти.

Были разработаны три способа активного учета ограничений как при разбиении исходной области П⁰ на подобласти, так и при дальнейшем поиске глобального минимума в каждой из подобластей.

Первый способ самый простой в вычислительном отношении, но он самый затратный -последовательно генерируются пробные точки (в П⁰ или в подобластях, на которые она разбита) и из них оставляются только те точки, которые удовлетворяют исходным ограничениям неравенств. Чем меньше объём допустимой области, тем больше число безрезультатных проб. В этом основной недостаток данного способа учёта ограничений неравенств и соответственно первого алгоритма поиска главных минимумов.

Второй способ базируется на изменении минимизируемой функции в пробных точках. Во-первых, она берётся в относительных величинах, а во-вторых, к ней добавляется штрафная компонента (тоже в относительных величинах), построенная по функциям фj(х), входящим в левую часть ограничений неравенств, в тех точках, где ограничения нарушены. При этом в расчётах участвуют только исходные пробные точки фиксированного объёма (n0 или n). Более – 336 – тонкий учёт ограничений в пробных точках, не попадающих в допустимую область, приводит к существенному сокращению числа генерируемых пробных точек. Особенно эффективен этот способ учёта ограничений при стремлении к нулю объёма допустимой области.

Третий способ позволяет учесть нарушаемые ограничения за счёт расширения нормированного ядра в алгоритме расчёта рабочего шага и размеров прямоугольной области для пробных движений следующего шага. Появляются (в виде произведения) дополнительные ядра для относительных величин нарушаемых ограничений. Сила этого способа такая же, как и предыдущего, но он несколько сложней в настройке вида вводимых ядер и в подборе их коэффициентов селективности.

Первый алгоритм (с использованием пробных точек внутри допустимой области)

В заданной прямоугольной области поиска П⁰ последовательно равномерно размещаются пробные точки, и из них формируется n ⁰ точек, попадающих в допустимую область ()                0

(2). Разбиение пробных точек x, i = 1, n на группы точек, тяготеющих к главным минимумам, производ ится следующим образом. В пробных точках вычисляется функция качества (          r( i )                о

I ( x ⁽ ) ) = I ⁽ ) , г = 1, n и отыскивается такая точка x min , которая соответствует наименьшей величине I_mi„ = min{ I ⁽ ) , i = 1, n }. Затем просматриваются все остальные пробные точки (кроме x _min) и из них отбираются те точки x ⁽‘ ) , которые расположены в окрестности x _min, например, в соответствии с условием: x v¹ ) - x v _min| x 0 / c , v = 1, m . Найденные точки образуют первую группу точек, множество номеров которых обозначим через M_n i , где n 1 - мощность множества M n 1 . Если мощность множества меньше, чем некоторое n _min (в представленном далее примере n min =5), то это множество удаляется как малозначимое. Оставшиеся пробные точки по той же схеме разбиваем на группы точек, пока общее количество групп не станет равным заданному количеству n ГЛ МИН главных минимумов или в исходной выборке не останется пробных точек.

Параметр c >1 определяет размеры подобластей и задается исследователем пока интуитивно на основе априорной информации о функции качества, требуемого количества n _{гл мин} главных минимумов и объема начальной выборки.

После разбиения исходной области на подобласти можно использовать информацию, содержащуюся в пробных точках из каждой подобласти, для получения уточненных значений 0

точки x подобл (центр подобласти), в среднем более тяготеющей к экстремуму, и интервалов варьирования A x ⁰ _одобл (размер подобласти), необходимых для второго этапа поиска.

0              0

x подобл и A x _подобл при поиске главного минимума в каждой подобласти, например в первой из них, рассчитывают по формулам

- о       =        i )Л i)                 i)   =   Ps (gm )n)      (*)   : I(‘) - Imin xv,подобл    2^ xv ps,min’ v   15m, ps,min     y’ / (j)\ , gmin f ^

ieMn,                            ^ps(gmin)        I max Imin j e M„,

Ax0   _

^ x ^v .подобл

f

n

\ 1/ q

= Yq- b; °- Э « "-Г ^рт

-   1 z

^ 1 M ,

s ,min

V

, v = 1, m , q = 1,2, - .

()                                                       )

Здесь: I min = ^{mln{ I} , ^{1 G} M_{n i} }, I max = ^max{ I , ^{1 G M} n 1 Y; P s ⁽ g ) ^- ядра; u v ^- р^авномер^но распределённые в интервале [-1; 1] числа.

При поиске главных максимумов расчёт x0подобл и Nx0 подобл ведётся аналогично вышепри ведённому, только ядра psmin заменяют на psmax

P s ( g m ax) до z р_$ ( g J ) , g ^max

J ^e M ni

max

A I max

I ( i )

I min

На этом первый этап (разбиение исходной области на подобласти) считается завершен- ным.

На втором этапе производится отыскание экстремумов в каждой найденной подобласти. При этом к неравенствам (2), которые входят в исходную постановку задачи, добавляются неравенства, определяющие прямоугольные подобласти, найденные на этапе разбиения исходной области на подобласти. Добавление таких неравенств не дает алгоритму выходить за границы этих подобластей и исключает многократные попадания в один и тот же экстремум.

Опишем алгоритм движения к минимуму на ( l +1)-м шаге, если на предыдущем шаге был получен вектор искомых переменных x^l , построенный на основе метода усреднения координат, он имеет вид:

х^{1 +1}= х ' +Ах ' и - и - = У и^р)⁰- v = 1 т x ^V     x _v ⁺ а х _v u _v ,_mm, u ^v ,_mln ^ u _v p s ,_mm, V 1, m ,

' ¹

( - )    , p s ( g mm ₌ 1

ps ,min    n            , g min    Ф z ps (gmin)         1 max

—

I min

¹ min

( n              AV q ____

^ x V + 1 = _Y ,^ x . I у | _u ( i ) | q p( i min | , _v = V, m , l=0, 1, 2, __;

L i=1                 J x0 = x Оодобл, Ax0   \< Оодобл; [0 < Yq, q е{1Л-},° < s ].

(j) (j)

Здесь: I_ = min{ I i = 1, „} , I „„ = maxi I J = 1, n )^; s ^- коэффициент селективности ядра p s (•); в переменных up , p s mi_n для упрощения записи опущен номер итерации l ; всегда ⁰ ^ g m L ^ ¹ . Ядра & нормированы ^{на системе} n пробных точек: z p si m„ = 1.

i = 1

Перед совершением ( l +1)-го рабочего шага при получении пробных точек x ^{( 1} ) , z = 1, n , последовательно генерируются точки (равномерно распределённые) в прямоугольной области П ¹ с центром в точке x^l :

x^z) = xV +AxV - u^^, uv e [-1; 1], v = 1, m, i = 1,2,.., и из них оставляется n точек, попадающих в допустимую область X. Пробные точки лежат в области X =П ПX. В пробных точках вычисляется минимизируемая функция г-i), i = 1, n, и на (i)

основе этих экспериментальных данных [ x _v , v = 1, m , 1 ⁽ i ) , z = 1, n ] совершается вышеприведённое рабочее движение и пересчитываются размеры области поиска.

V

Критерием останова процесса поиска обычно служит условие уменьшения размера облас^ти варьирования A x до заданной величины. _max(| ^A x A. v = l? m i д = .

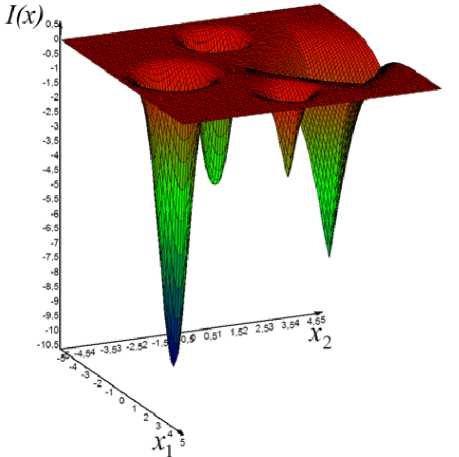
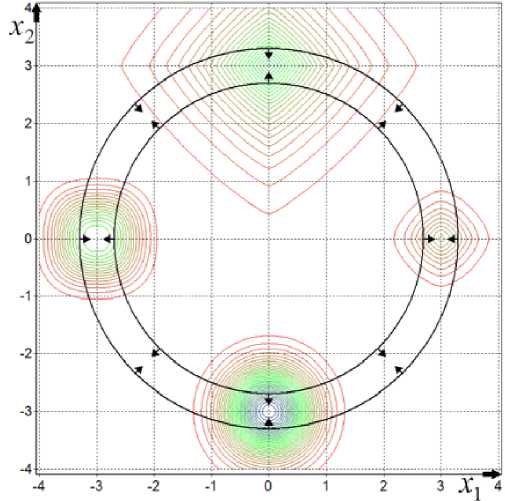
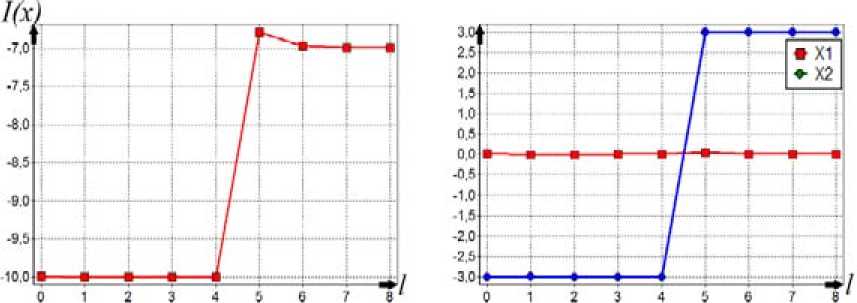
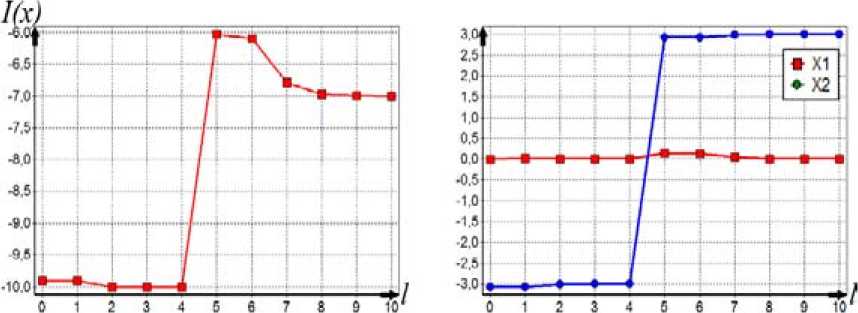
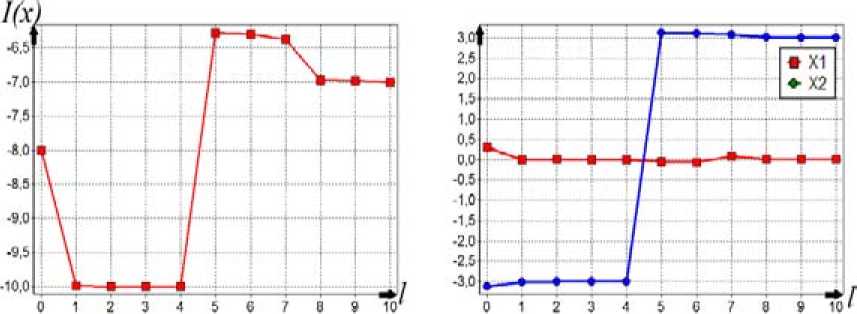
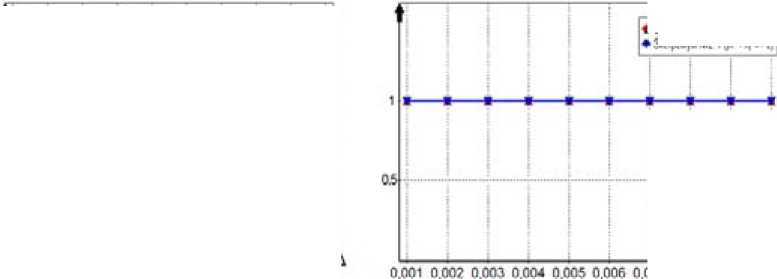
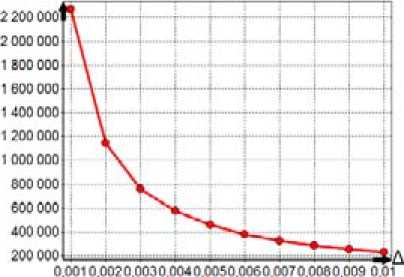
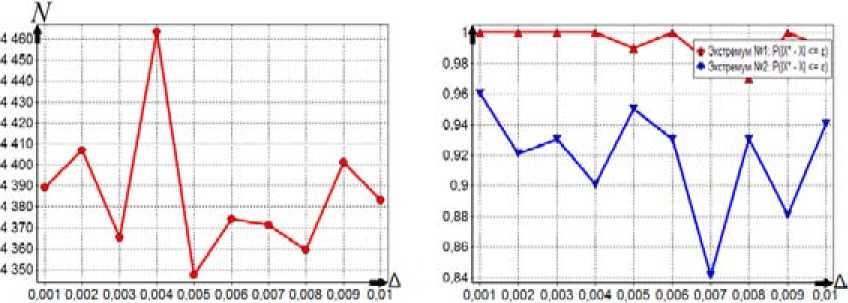
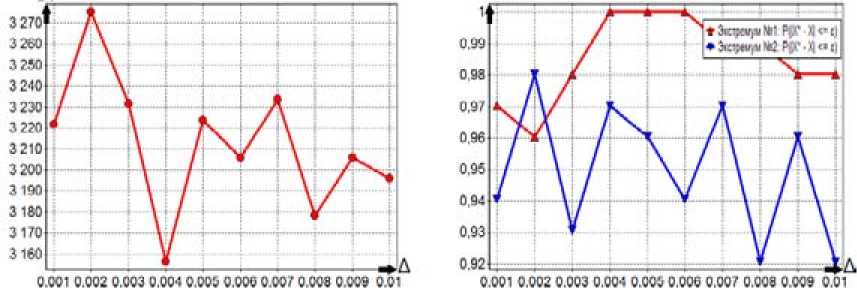
ps(g) на интервале изменения 0

Ps (g) = (1 - g ) , r = 1,2,3,.... Коэффициент s для степенных ядер лежит в широком диапазоне целых положительных чисел и подбирается сравнительно просто.

Второй алгоритм (с переходом к штрафной функции)

В области П⁰ равномерно размещаются n⁰ пробных точек. В них вычисляется штрафная функция:

Т (i)

I•(x^и) = 2-

Imax

А

I^min

А

"I min

Ф,( X^W)-Фу-min . _r(0 — + а-maxi-^--------^J-—, j еJ el, m i,

^фj max

^фj min

i = 1, n⁰, a>0.

.                    ТТЛ                 .         .                                                                         1

Здесь множество J⁽i) включает только номера тех функций ограничений, для кото-

(i)

рых ограничения нарушены: при j е J⁽¹) е 1, m1 всегда 0 < ф_у (x⁽¹)); I_min= min{Г , i = 1, n}, Im., = ™^axl I * i^),i = 1.» I; для ^каждого фиксированного j: фу_m_ = min(^j(x“’), i :0 < ф,( x¹'¹)}, _Vj- = ™Ф,^(x"Xi:O <,.(^x"'»;

Если при некотором j=l множество {i :0 < фг(x())} пустое, то этот номер l не входит l во множество j(1) (для каждого фиксированного i). Для пробных точек, в которых ни одно неравенство не нарушено (т.е. множество j(i) пустое), штрафная добавка берётся равной нулю.

Если при некотором j=l множество {i :0 < ф₁ (x⁽i))} состоит из одного элемента, то соответствующий элемент в (4), входящий под оператор max{}, полагаем равным 1: ^Ф (^^-ф. _₁ДФ₁ _ ^-ф. Л

Далее, отыскивается точка x , которая соответствует наименьшей величине ~              ,~i i)            0                              ,

Imin = min{I⁽), i = 1, » } штрафной функции. Дальнейший отбор точек, находящихся в окрестности xmin, и разбиение на группы точек проводится так же, как и в первом алгоритме.

После разбиения П⁰ на подобласти поиск минимума в каждой из подобластей ведется так же, как и в первом алгоритме, но пробные точки размещаются равномерно по всей подобласти (а не в её части, как в предыдущем алгоритме), и вместо исходной функции I⁽ⁱ⁾ используется штрафная функция Т^ (4).

Третий алгоритм (с переходом к многомерным ядрам)

В области П⁰ равномерно размещаются n⁰ пробных точек и в них вычисляются многоэкстремальная функция и функции ф_у ограничений: I(x⁽¹)) = I⁽i), ф_у(x⁽i)), j = 1, m, i = 1, n⁰. Далее формируются нормированные ядра pSi):

P.s (g⁽i⁾) ПP2,S (gj⁾)

£ P1, s (g⁽")) П p 2, s (g 'r))

H=1               j_eJ⁽^)

Здесь при минимизации g⁽i) = g(i)_n

I (i)

A

I max

A                                                          A

, при^{максимизации}g ^i)=gmm ax=-m^ I min                                       I max

I (i)

;

min

а также g⁽i) = g_j

ф (x⁽ⁱ⁾) - ф_

-j— ---j^min-, j = 1, m1; P 1.S — ядро по оптимизируемой функции; p2 s - ядро по

Фj ,max

Фу ,mrn

ограничениям; Imax, Imi фj max, фj min для каждого фиксированного j, а также множество J(i) те ,, же, что и во втором алгоритме.

(i)

Если при некотором j=l множество {i: 0 < ф^(x^v J} состоит из одного элемента, то аргумент ядра p2,S полагаем равным 0,75. Это значение было получено экспертным путем. Если во всех пробных точках неравенства не нарушены, то ядра становятся одномерными и зависят

n только от оптимизируемой функции: pSi’ = Р1 $(g<0)/£Pls(g(ц’).

,=1

Далее отыскивается точка xmin, которая соответствует наибольшей величине нормированного ядра pSi’. Отбор точек, находящихся в окрестности x_min, и разбиение на группы точек проводятся так же, как и ранее.

После разбиения П⁰ на подобласти поиск минимума в каждой из них ведется так же, как и для первого алгоритма, но вместо размещения точек только в допустимой области точки размещаются равномерно по всей подобласти поиска, и расчет нормированных ядер pSim_inпроизводится по формуле (5).

Численный пример

Исследуем поведение алгоритмов при сужении допустимой области. Рассмотрим четырёхэкстремальную потенциальную функцию, построенную за счёт применения операции min к четырём элементарным экспоненциальным потенциалам:

^{1 (}x ’ = Л, iexpuit-31'5 +|x .f⁵]!.

-5exp{-2.5[| x1 + 3|25 +1 x2 25]},(6)

-7exp{-[| X' |^1.2+1 x2 -3 |^L2]},-10exp{-2[| X' |²+ | x. + 3 |²]}}

Допустимая область имеет вид кольца шириной Δ:

x2 + x22 < (3 + -) и x2 + x22 > (3--).(7)

• 1        2^                      12^

На рис. 1 представлен пространственный вид функции (6). Она имеет минимумы в точках (–3; –0), (0; 3), (3; 0), (0; –3) и принимает в них соответственно значения (–3), (–5), (–7), (–10). На рис. 2 приведены линии равных уровней функции (6) и допустимая область (7) при Δ=0,4.

Все три вышеописанных алгоритма хорошо справляются с поиском условного глобального экстремума при достаточно широкой допустимой области (большом Δ).

На рис. 3-5 отражено изменение по итерациям минимизируемой функции и координат при поиске двух главных минимумов функции (6) при ограничениях (7) и Δ=1,01.

Как видно из рис. 3, для первого алгоритма исходная точка поиска находится в малой окрестности истинного решения. Данный факт обусловлен тем, что пробные точки размещаются только в допустимой области, она для данного примера имеет малую площадь.

Как видно из рис. 4, второй алгоритм достаточно быстро отыскивает главные экстремумы, совершая при этом на два-три шага больше чем первый алгоритм. Это обусловлено тем, что – 340 –

Рис. 1. Потенциальная функция (6)

Рис. 2. Равные уровни функции (6) и допустимая область (7) при Δ=0,4

Рис. 3. Процесс поиска двух главных минимумов первым алгоритмом

Рис. 4. Процесс поиска двух главных минимумов вторым алгоритмом

Рис. 5. Процесс поиска двух главных минимумов третьим алгоритмом второй алгоритм производит поиск по области, в то время как первый алгоритм уже на первой стадии нашел хорошее приближенное решение.

Как видно из рис. 5, третий алгоритм ведет себя примерно так же, как и второй.

Проведем исследование поведения алгоритмов для узкой допустимой области. Для этого будем менять ширину допустимой области А от 0,001 до 0,01 с шагом 0,001 и усреднять полученные значения на каждом шаге по 101 запуску. Используем следующие показатели качества работы алгоритмов: N – количество попыток размещения пробных точек и оценки вероятности отыскания «истинных» главных экстремумов - Р(|x - x| < е).

Первый алгоритм. Считаем, что n⁰=500, область поиска с центром x⁰=(0; 0) и размером Аx⁰= (4; 4), q=2, yq=1,2, ядро по функции качества параболическое с коэффициентом селективности s=100, размер выборки при поиске экстремума в подобласти n=150. На рис. 6 представлены графики описывающие поведение алгоритма. Первый график показывает усредненное значение N для каждого Δ, второй – оценку вероятности отыскания истинного экстремума.

Как и ожидалось, в первом алгоритме уменьшение ширины допустимой области А приводит к резкому увеличению количества попыток генерации пробных точек. Как видно из рис. 6, для отыскания экстремумов при ширине А=0,001 было предпринято 2,2-106 попыток размещения пробных точек. Оценка вероятности отыскания истинного экстремума очень высока и равна единице, это объясняется тем, что узкая допустимая область практически не оставляет «свободы» поиска для алгоритма. С ростом Δ уменьшается количество попыток размещения пробных точек, так как допустимая область становится шире и в нее легче попасть. Следует отметить, что такое большое число попыток размещения пробных точек при наличии узкой допустимой области делает этот алгоритм практически непригодным для использования при решении практических задач, так как в практических задачах размещение пробной точки эквивалентно проведению дорогостоящего эксперимента.

Второй алгоритм. Зададим следующие параметры алгоритма: размер выборки для выделения подобластей n0=500, область поиска с центром x0=(0; 0) и размером Аx0= (4; 4), q=2, yq=1,2, ядро по функции качества параболическое с коэффициентом селективности 5 =200, размер выборки при поиске экстремума в подобласти n=150, штрафной коэффициент α=1. На рис. 7 представлены графики, описывающие поведение алгоритма. Первый график показывает коли- t>WW W-HaQ kw*W № 4 et)

Рис. 6. Зависимость показателей качества работы первого алгоритма от Δ

007 0,006 0,009 0.01

N

Рис. 7. Зависимость показателей качества работы второго алгоритма от Δ

Рис. 8. Зависимость показателей качества работы третьего алгоритма от Δ чество попыток генерации пробных точек, второй – оценку вероятности отыскания истинного экстремума.

Из графиков наглядно видно, что количество попыток размещения пробных точек в четыреста раз меньше, чем для первого алгоритма (для Δ =0,001). Оценка вероятности отыскания истинного решения достаточно высока и в среднем равна 0,95. Качество работы алгоритма не зависит от ширины допустимой области. Этот алгоритм более прост в настройке, чем третий алгоритм, так как необходимо настроить одно ядро, а у третьего алгоритма – два.

Третий алгоритм. Зададим следующие параметры алгоритма: размер выборки для выделения подобластей n⁰=400, область поиска с центром x⁰=(0; 0) и размером Ax⁰= (4; 4), q=2, yq=1,2, ядро по функции качества параболическое с коэффициентом селективности s=50, ядро по ограничениям параболическое с коэффициентом селективности s=100, размер выборки при поиске экстремума в подобласти n=100. На рис. 8 представлены графики, описывающие поведение алгоритма. Первый график показывает количество попыток генерации пробных точек, второй – оценку вероятности отыскания истинного экстремума.

Из графиков видно, что так же, как и для второго алгоритма, количество попыток и оценки вероятности отыскания истинного решения не зависит от ширины допустимой области. При этом количество попыток в шестьсот раз меньше, чем для первого алгоритма (для Δ=0,001). Оценка вероятности отыскания истинного решения достаточно высока и в – 344 – среднем равна 0,95. Третий алгоритм работает немного лучше второго, но он более сложен в настройке.

Программная реализация алгоритмов

Продемонстрированные алгоритмы входят в состав пакета глобальной оптимизации Global Optimizer v2.0, в котором также представлены основные алгоритмы глобальной оптимизации, базирующиеся на методе усреднения координат. Пакет реализован на языке Delphi с использованием среды визуального программирования Delphi 2010 фирмы Embarcadero Technologies и функционирует в операционной системе из семейства Windows 2000/XP/Vista/7.

При проектировании программных алгоритмов поиска главных минимумов был использован объектно-ориентированный подход. Алгоритмы реализованы как надстройка над алгоритмами поиска глобального экстремума, описанными в монографии [2]. Этот подход позволяет распараллелить поиск главных экстремумов и тем самым значительно повысить скорость работы алгоритма. Этот вариант требует специальных исследований.

Заключение

Алгоритмы поиска главных экстремумов привлекают своей простотой, сравнительно небольшими вычислительными затратами, высокими точностными показателями.

Проведенные исследования выявили, что все три алгоритма примерно одинаково эффективны, если допустимая область достаточно большая и количество ограничений сравнительно невелико. При сужении допустимой области и увеличении количества ограничений первый алгоритм становится неэффективным, так как требует значительного количества попыток размещения пробных точек и вычислений в них функций ограничений, тогда как второй и третий алгоритмы от этого свободны.

Статья публикуется при поддержке Программы развития Сибирского федерального университета