Поиск эталона измерений в модификациях МАИ первого поколения для методики выбора эффективных проектов и других областей науки
Автор: Шагеев Д.А.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Экономика и управление
Статья в выпуске: 1 (91), 2022 года.
Бесплатный доступ
Автор в очередной раз продолжает цикл публикаций в области развития сформулированных ранее ядра и двух фундаментальных положений методики выбора эффективных проектов через разные решения модификации метода анализа иерархий (МАИ) для финансовой, математической и др. направлений в науке. Уделено особое внимание повышению точности измерений матричных, нормированных и векторных оценок для развития универсальных свойств МАИ за счёт следующих решений, обладающих разными качествами научной новизны: введения новых формул вычисления матричных оценок с подробными инструкциями их применения; предложения девяти разных вариантов комбинаций МАИ, в каждой из которых включено четыре классификатора (AHPMS-М1.N, AHPMS(AM)-М1.N, FAHPMS-М1.N и AHPDD-М1.N) на базе целочисленной и дробночисленной 9-балльной шкалы Т. Саати с восемью интервалами измерения. В статье представлены объёмные экспериментальные данные, при помощи которых доказана научная состоятельность указанных и уже ранее раскрытых решений, обладающих научной новизной в направлении повышения точности измерений в МАИ через разные модификации первого поколения. Результаты эксперимента действительно позволили найти и доказать правомерность использования в науке эталона измерения из 9-ти предложенных комбинаций. Отличительные особенности эталонной комбинации следующие: шкала дробночисленная [0; …;8]+1 в 8 основных интервалах измерения; при оценивании двух равных объектов (Аi(j)= Аj(i)) их матричные оценки равны единицам (0+1=1); указанные новые решения. Таким образом, полученный опытным путём и подтверждённый эталон измерения из первого поколения модификаций МАИ рекомендуется использовать не только в методике выбора эффективных проектов, но и в др. областях науки с учётом его универсальных свойств.
Маи, анализ иерархий, измерения, шкалы, экспертные оценки, проекты, управленческие решения
Короткий адрес: https://sciup.org/140293787
IDR: 140293787 | УДК: 65.012.123,
Текст научной статьи Поиск эталона измерений в модификациях МАИ первого поколения для методики выбора эффективных проектов и других областей науки
This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License
Шагеев Д.А. Вестник ВГУИТ, 2022, Т. 84, №. 1, С. 388-410 Введение
Автор продолжает цикл публикаций в области развития методики выбора эффективных проектов через разные модификации метода анализа иерархий (МАИ). Кроме того, через предлагаемые модификации осуществляется прирост научного знания не только в финансовой науке, но и в математической науке для универсализации этого знания и возможности применения в др. областях науки. В данной, уже четвёртой по счёту статье представлены результаты эксперимента всех девяти ранее описанных комбинаций [11] для классификаторов первого поколения AHPMS-М1.N, AHPMS(AM)-М1.N, FAHPMS-М1.N и AHPDD-М1.N, чтобы опытным путём найти эталонную комбинацию, позволяющую максимально точно/тонко производить измерения в МАИ. Расшифруем эти классификаторы:
-
1) AHPMS-М1.N – (Analytic Hierarchy Process and Mathematical Statistics) – аналитическая иерархия в сочетании с методами математической статистики;
-
2) AHPMS(AM)-М1.N – (Analytic Hierarchy Process and Mathematical Statistics (Artificial Measurement)) аналитическая иерархия в сочетании с методами математической статистики на базе искусственных измерений;
-
3) FAHPMS-М1.N (Fuzzy Analytic Hierarchy Process and Mathematical Statistics) – нечёткая аналитическая иерархия в сочетании с методами математической статистики;
-
4) AHPDD-М1.N (Analytic Hierarchy Process and Determine Data) – аналитическая иерархия в сочетании с детерминированными данными.
Первая цифра после символа «М» (Modification) обозначает принадлежность классификатора к первому поколению модификации МАИ «1». Второе поколение модификаций, которое будет существенно отличаться от первого, обозначим цифрой два «2» (будет описано в др. статье автора). Вторая цифра после символа «М» обозначает порядковый номер модификации «N».
Проведён анализ разных научных источников в области проблем измерений в МАИ за последние 40 лет [11]. Отметим только некоторые научные труды, которые прямо, либо косвенно связаны с отраслью научного знания «экономика и управление» в виду ограниченности объема статьи.
-
Т. Саати [8, 9, 21] автор МАИ решал практические задачи в следующих направлениях: «Интегрированное нахождение приоритетов ресурсов для развивающихся стран»; «Выбор и распределение ресурсов в области энергетики»; «Экономика и управление медицинским обслуживанием». Не уделял внимания повышению
К. Бенмоус, М. Лаазири, С. Кхаулджи, М.Л. Керкеб и А.И. Ямани [13] используют МАИ через компьютерные системы с учетом признака эргономичности критериев для оценки интерфейсов в области маркетинга. В статье прослеживается факт, что авторы столкнулись с ограниченностью измерений парных оценок по 9-балльной целочисленной шкале Т. Саати.
В статье М.А. Эллиотта [14] представлена хорошая попытка решения проблемы точности измерений в МАИ за счёт выбора разных шкал для решения экономических проблем выбора, но при этом сам механизм вычислений в МАИ оставлен без изменений. Похожие исследования в области выбора шкал обнаружены в работе Дж. Франек [15]. А. Гнанавелбабу и П. Арана-гири [16] в своём исследовании используют МАИ для решения проблемы сокращения отходов и др. видов потерь по типу «Муда» на производстве. При этом модифицируют МАИ с учётом методов нечётких множеств Л. Заде. Это не помогло авторам повысить точность измерений матричных оценок и векторов приоритетов т.к. шкала и механизм вычислений в МАИ остались стандартными, только представляются по типу треугольного нечёткого числа.
-
А. Ишизака, А. Лабиб и Б.Р. Мисариган-да [18, 19] представляют эксперименты по
коррекции вычислений матричных оценок, векторов приоритетов, вопросы их синтеза и т.д., в том числе и при помощи компьютерных программ для разработки эффективных управленческих решений. Повышения точности измерений есть, но они не принципиальные т. к. шкала измерений матричных оценок остается целочисленной – 9-балльной.
Е.Ц. Харрингтон [17] предложил универсальную вербально-числовую шкалу через функцию желательности. Таким образом – это дало основания для принятия этой шкалы в исследованиях экономического и управленческого направлениях многими отечественными и зарубежными авторами. Шкала Е.Ц. Харрингтона позволяет делать интервальные уточнения измерений в МАИ [11] – это еще одно из действий на пути повышения точности измерений.
Особое внимание обращается разными исследователями на проблему эффекта смены степеней предпочтений («Rank Reversal» - RR). Одними из первых осветили эту проблему В. Белтон и Т. Гир, анализируя возможности классического МАИ для распределения экономических ресурсов в области управленческих решений [12]. Их вывод в исследовании – это
Т. Саати совместно с И. Миллетом попытался найти решение проблемы RR при помощи разных форм иерархического синтеза (свёртки локальных векторов) [20]. Ещё одна попытка решить проблему «RR» предпринята Ин-Мин Ваном и Т.М.С. Эльхагом в научной области управленческих решений [22]. Несмотря на указанные [12, 22] и др. попытки решения проблемы RR, Т. Саати и М. Сагир констатировали «Сохранение и изменение рангов, столь фундаментальные в процессе принятия решений, были неразрешенной проблемой в области экономики и теории полезности и попали в фокус внимания, когда был разработан процесс аналитической иерархии, поскольку он использует парные сравнения, которые неизбежно делают приоритеты альтернатив взаимозависимыми. В этой статье обобщаются важные вопросы, которые могут играть роль в сохранении и изменении ранга с помощью контрпримеров в области управленческих решений, чтобы показать, что сохранение ранга во всех ситуациях является неправильным.» (перевод с англ., ист. [21]). Таким образом проблема RR так и не была полностью решена по мнению Т. Саати.
В.М. Картвелишвил и Э.А. Лебедюк [1] также отмечают, что проблема RR до сих пор не решена в науке подтверждая слова Т. Саати и М. Сагира [21]. По мнению авторов, эффект RR искажает результаты исследований на базе МАИ в экономике и менеджменте.
В.А. Титов и И.Г. Хайрулин в своей работе [10] отмечают проблему выбора формы свертки локальных векторов приоритетов (операция иерархического синтеза) для риск-анализа альтернативных проектов. Авторы утверждают, что при аддитивной и мультипликативной свертке получаются разные результаты измерений результирующих векторов приоритетов для МАИ, в качестве компромиссной альтернативы В.М. Ногиным [6], предлагается нелинейная форма. В.М. Ногин описывает нелинейную форму свертки критериев на примере решения проблемы оценки и выбора инвестиционных проектов.
В.Б. Коробовым и А.Г. Тутыгиным [2] уделяется особое внимание шкале отношений Т. Саати и проблеме «идеального» эксперта. Показано, что шкала отношений не является инвариантной, а отношение согласованности, использующее понятие «идеального» эксперта, не может быть применено в качестве критерия оценки качества работы эксперта в поле управленческих решений. Метод представляет
Похожую критику [2, 10] по поводу шкалы измерений и форм свертки в МАИ излагает В.Г. Митихин [3, 4]. К указанной критике присоединяются И.Н. Мощенко и Е.В. Пирогов [5], О.В. Подиновская и В.В. По-диновский [7] с её дополнением – эффектом RR. Эта группа авторов занимается исследованиями оценки и выбора инвестиционных проектов в поле управленческих решений через МАИ.
В результате дискуссии с учётом материалов из ист. [11], выявлена и подтверждена проблема недостаточной точности измерений в МАИ Т. Саати по следующим причинам:
-
1) целочисленная 9-балльная шкала экспертных суждений;
-
2) эффект RR;
-
3) неясность выбора наиболее корректной формы свёртки локальных векторов приоритетов;
-
4) др. стандартные процедуры в МАИ.
В дискуссионном поле указаны авторы, которые описывали проблемы измерений МАИ в процессе решения экономических и/или управленческих задач – например оценка и выбор эффективного проекта, как оказалось – это самое распространённая прикладная область исследования. Именно в процессе и по результатам исследований описываются причины, из-за которых появилась данная проблема. Поэтому важно эту проблему решать не только с позиции науки математики, но и с позиции математики-экономики-управления . Именно такая триада принята в данной статье, где в следующих разделах описываются решения проблемы измерений через эксперимент оценки и выбора эффективного проекта на примере критерия NPV (Net Present Value – чистый дисконтированный доход проекта).
Суть авторского решения сводится к поиску эталона измерений в модификациях МАИ первого поколения для:
-
1) решения проблемы недостаточной точности измерений в МАИ за счёт выявления и использования резервов;
-
2) исключения возможности появления ошибок в процедурах реализации МАИ;
-
3) «тонкая оценка» объектов с минимальными отличительными признаками;
-
4) использования объектов, привязанных к измерениям.
Шагеев Д.А. Вестник ВГУИТ, 2022, Т. 84, №. 1, С. 388-410
Таким образом в экономике и менеджменте появится новая альтернатива в части МАИ, которая позволит экономистам, управленцам и др. заинтересованным сторонам выполнять прикладные исследования без искажений и ошибок, повышая качество управленческих решений.
Методы исследований
Цель эксперимента доказать научную состоятельность предложенных решений проблем [11] использования фундаментальной шкалы Т. Саати в форме разных модификаций для повышения степени универсальности применения МАИ в методике выбора эффективных проектов и др. областях науки за счёт повышения точности измерений. В частности предложены следующие решения: введения новых формул вычисления матричных оценок с подробными инструкциями их применения; предложения девяти разных вариантов комбинаций МАИ, в каждой из которых включено четыре классификатора (AHPMS-М1.N, AHPMS(AM)-М1.N, FAHPMS-М1.N и AHPDD-М1.N) на базе целочисленной и дробночисленной 9-балльной шкалы Т. Саати с разным количеством интервалов измерения; описания вариантов решения проблем измерения матричных оценок, образованных нестандартно измеренными объектами матрицы [11].
В качестве объекта исследования взята иерархия проблемы выбора эффективных проектов (рисунок 1), а предметом исследования выделены управленческие решения на базе показателей «NPV», принадлежащие ветке «инвестиционная эффективность» уровень иерархии четыре в форме локальных векторов
Предположим, что эксперт «n» уже выбрал одно значения «NPVi(j)» (Ai(j)) (выделено полужирным шрифтом) по каждому проекту из области определения нечётких множеств треугольного вида, млн руб.:
NPV1(1) = {8; 11,5; 14}; NPV2(2) = {10; 1 0,9; 12};
NPV3(3) = {51,2;61; 77};
NPV4(4) = {69; 77;83,4};
NPV5(5) = {81; 92; 108};
NPV6(6) = {137,2; 162; 173}.
Для удобства восприятия данных вместо формального обозначения матричных объектов Ai(j) подставлены: NPVi(j) = {nP^®; NPV^ ) ; NPV ‘ (i) } , где a, b и c – это нечётко-денежное выражение показателя NPV проектов [11]. Представим их в следующим виде, млн руб.:
NPV1(1) = {NPVg^NPV^NPVi^ NPV2(2) = {nPV20(2);N PV^NPV2®}; NPV3(3) = {nPV|1(32);NPV631(3);N PV3®}; NPV4(4) = {NPV 49(4) ;N PV^NPV4®}; NPV5(5) = {NPV85 15) ;NPV92 (5) ;N PV^®}; NPV6(6) = {NPVf^NPVf^N PVfH)}.
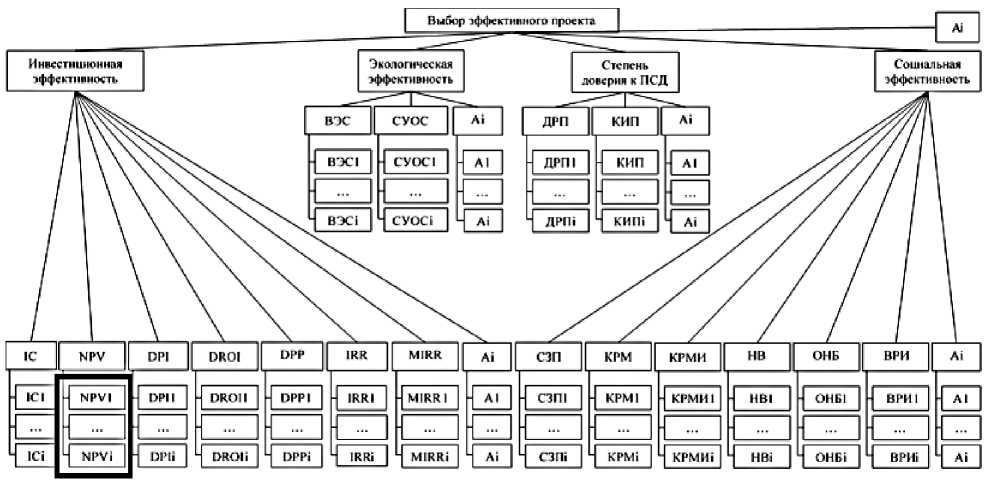
Рисунок 1. Иерархия проблемы выбора эффективного проекта
Figure 1. Hierarchy of the effective project selection problem
Shageev D.A. Proceedings of VSUET, 2022, vol. 84, no. 1, pp. 388-410
В примере объекты «NPV» специально пронумерованы в последовательности от меньшего к большему (ранжированы) для удобства реализации вычислений и восприятия данных. Таким образом выполнено первое правило [11] для корректного использования формулы 1 и 2, в котором требуется чтобы все объекты матрицы парных сравнений были привязаны к единому измерителю «NPV» и единому измерению «млн руб.». Для соблюдения и проверки научной состоятельности введённого
Таблица 1.
Варианты комбинаций выполнения разных условий при Ai(j) = Aj(i) > а^ = 0 v 1 и а --d = 0 v 1 в МАИ первого поколения модификаций для методики выбора эффективных проектов и др. областей науки*
Table 1.
Variants of combinations to fulfill different conditions when Ai(j) = Aj(i) > а^ = 0 v 1 and а 1- d = 0 v 1 in AHP of the first generation of modifications for the methodology of selecting effective projects and other fields of science *
|
Варианты шкал оценивания в МАИ первого поколения | Variants of assessment scales in the AHP of the first generation |
№ п/п № р/р |
Первое условие – диагональные оценки (d - diagonal) ау, баллы | The first condition is diagonal estimates (d - diagonal) ау, points |
Второе условие – не диагональные оценки (nd - not diagonal) ауd, баллы | The second condition is non-diagonal estimates (nd - not diagonal) аyd, points |
Классификаторы для вариантов комбинаций МАИ первого поколения модификаций | Classifiers for variants of combinations of AHP of the first generation of modifications |
|
Целочисленная [1; ...;9] только 8 основных интервалов измерения | Integer [1; ...;9] only 8 main measurement intervals |
1 |
Ai(j) = Aj(i) > аЛ = 1 |
Ai(j) = Aj(i) > ааd = 1 |
AHPMS-М1.1; AHPMS(AM)-М1.1; FAHPMS-М1.1;AHPDD-М1.1 |
|
2 |
Ai(j) = Aj(i) > а^ 0 |
Ai(j) = Aj(i) > ааd = 0 |
AHPMS-М1.2; AHPMS(AM)-М1.2; FAHPMS-М1.2; AHPDD-М1.2 |
|
|
3 |
Ai(j) = Aj(i) > а^ = 1 |
Ai(j) = Aj(i) > ааd = 0 |
AHPMS-М1.3; AHPMS(AM)-М1.3; FAHPMS-М1.3; AHPDD-М1.3 |
|
|
4 |
Ai(j) = Aj(i) > аЯ = 0 |
Ai(j) = Aj(i) > ааd = 1 |
AHPMS-М1.4; AHPMS(AM)-М1.4; FAHPMS-М1.4; AHPDD-М1.4 |
|
|
Дробночисленная [1; ...;9] в 8 основных интервалах измерения | Fractional [1; ...;9] in 8 main measurement intervals |
5 |
Ai(j) = Aj(i) > а^ = 1 |
Ai(j) = Aj(i) > ааd = 1 |
AHPMS-М1.5; AHPMS(AM)-М1.5; FAHPMS-М1.5; AHPDD-М1.5 |
|
6 |
Ai(j) = Aj(i) > аЛ = 0 |
Ai(j) = Aj(i) > ааd = 0 |
AHPMS-М1.6; AHPMS(AM)-М1.6; FAHPMS-М1.6; AHPDD-М1.6 |
|
|
7 |
Ai(j) = Aj(i) > аЛ = 1 |
Ai(j) = Aj(i) > ааd = 0 |
AHPMS-М1.7; AHPMS(AM)-М1.7; FAHPMS-М1.7; AHPDD-М1.7 |
|
|
8 |
Ai(j) = Aj(i) > аЛ = 0 |
Ai(j) = Aj(i) > ааd = 1 |
AHPMS-М1.8; AHPMS(AM)-М1.8; FAHPMS-М1.8; AHPDD-М1.8 |
|
|
Дробночисленная [0; ...;8] +1 в 8 основных интервалах измерения | Fractional [0; ...;8]+1 in 8 main measurement intervals |
9 |
Ai(j) = Aj(i) > ad 0 + 1 = 1** |
Ai(j)=Aj(i)>and = = 0 + 1 = 1** |
AHPMS-М1.9; AHPMS(AM)-М1.9; FAHPMS-М1.9; AHPDD-М1.9 |
|
Эталонная комбинация в первом поколении модификаций МАИ | Reference combination in the first generation of AHP modifications |
||||
*В границах иерархии могут применяться разные классификаторы в зависимости от характера, в какой-то степени имеющихся или вовсе не имеющихся измерений и измерителей объектов в матрицах парных сравнений. |
Different classifiers can be used within the boundaries of the hierarchy depending on the nature, to some extent, of existing or not at all available measurements and meters of objects in the matrices of paired comparisons.
**Действие +1 необходимо для приведения матричных оценок a d и ayd в соответствие с ац v Зу из формулы 1. |
Action +1 is necessary to bring matrix estimates ad and 3yd in accordance with с Зу v ау from formula 1.
Матричные оценки а -j v а ■■ , баллы, числялись по следующим формулам [11]:
|Ai(j)-Aj(i)| а1- v а1j = S S =
_ |Ai(j)-Aj(i)| [ 1 ;_;9],М 1.1 - 4
= <(A1(j) max . -Ai(j) min . )/9) Ь [1;^;9],М 15-8 ,
вы-
|AiCj)-Ai(i)| _ d1j v а1j =
|A1(j)-Aj(i)|
( ( Ai ( j)m ax. ~Ai(j )m in.) '
SS
; 8] + 1, М1.9 ,
где а 1 j - условно объективная матричная оценка, освобождённая от субъективных суждений экспертов в классификаторе типа AHPDD-М1.N, для повышения точности измерений рекомендуется округлять до десятитысячных или стотысячных (всегда выставляется в ячейку с ориентацией на большую величину в паре Ai(j), а обратная оценка вычисляется по стандартному правилу в МАИ: 1/ ац .), баллы; а 1- - субъективная матричная оценка, выраженная при помощи экспертного
Шагеев Д.А. Вестник ВГУИТ, 2022, Т. 84, №. 1, С. 388-410 суждения – n, в классификаторах типа AHPMS(AM)-М1.N и FAHPMS-М1.N, для повышения точности измерений рекомендуется округлять до десятитысячных или стотысячных (всегда выставляется в ячейку с ориентацией на большую величину в паре Ai(j), а обратная оценка вычисляется по стандартному правилу в МАИ: 1/3-j .), баллы; ˅ – операция дизъюнкция (действие – или) из математической логики, которая позволяет по формуле 1 и 2 вычислить а ij или а ■j при наличии разных условий измерения для разных классификаторов первого поколения МАИ; Ai(j) и Aj(i) – объекты матрицы парных сравнений, измеряемые в каких-либо единых единицах измерения при помощи каких-либо единых или смежных измерителей, ед. изм.; SS – Step of the Scale – это расчётный шаг шкалы, для повышения точности измерений рекомендуется его округлять до десятитысячных или стотысячных, баллы; Ai(j)max. и Ai(j)min . – максимальное и минимальное измерение объекта матрицы парных сравнений из числа её объектов Ai(j) в каких-либо единых единицах измерения при помощи каких-либо единых или смежных измерителей, баллы; 8 и 9 – очень сильное и абсолютное предпочтение по шкале Т. Саати, баллы; +1 – необходимое действие для комбинаций М1.9 чтобы избежать грубые ошибки измерений и получения возможности корректного вычисления показателя согласованности матричных оценок – ОС при соблюдении определённых условий в модифицированном исполнении МАИ; М1.1-4, М1.5-8 и М1.9 – сокращённые название классификаторов для вариантов комбинаций МАИ первого поколения модификаций (таблица 3) принадлежащих « ∈ » целочисленной шкале [1;…;9] и дробночисленной [1;…;9] в формуле 1, дробночисленной [0;…;8]+1 в формуле 2.
В указанном случае эксперимента будем производить вычисления aU по формуле 1 и 2, для классификаторов FAHPMS-М1.N. При этом подразумевается, что эксперт работал только с нечёткими измерениями объектов матрицы «NPV». В самой матрице он не работал, предоставлял только данные для этой экспериментальной работы. В результате использования формулы 1 и 2 находились числовые отметки для матричных оценок по целочисленной [1; …;9]
и дробночисленной модифицированной шкале Т. Саати в диапазоне [1; …;9] и [0; …;8]+1.
Сам процесс расчётов матричных оценок по формуле 1 и 2 сосредоточен в ячейках под диагональю равнозначно измеренных объектов,
а зеркальные над диагональными их значениями определены по стандартному условию МАИ – 1/а■■ . Эти действия предприняты также для удобства реализации вычислений и восприятия экспериментальных данных в следствии реализации операции ранжирования входных данных.
Нормирование матричных оценок (n■■) и вычисление локальных векторов приоритетов (ԝ Ai ) эксперта – n, реализовывалось по следующим общеизвестным формулам [8, 9, 11]:
n0 =∑ к , (3)
∑i=i aij
∑ LnS
ԝAi = ∑ , (4)
где ∑i=l а jj – сумма оценок попарного сравнения объектов Аi(j) в пределах каждого столбца матрицы (j=const), баллы; ∑j njj – обобщённая величина нормированных балльных оценок в пределах каждой строки матрицы (i=const); k – количество объектов Ai(j) уровня иерархии, сравниваемых в границах матрицы.
Для проверки согласованности оценок в границах матрицы применялся показатель отношение согласованности (ОС) (CR – Consistency Ratio) по формуле [8, 9, 11]:
CR= s , (5)
где CI – (Consistency Index) индекс согласованности; RI (Random Index) – табличный индекс согласованности определённой размерности матрицы, заполненной при случайном моделировании [8, 9, 11], в нашем эксперименте для матрицы размерностью 6×6 принимаем значение 1,24.
При этом должно соблюдаться условие: ОС<0,1. В свою очередь, CI:
CI
^max x x-1 ,
где λmax – собственное число матрицы парных сравнений, а х – размерность матрицы.
Далее, λ :
λmax =∑j=l а ij ԝAi . (7)
Результаты исследований
С учётом изложенного материала в данной статье, указанных характеристик эксперимента и формул 1-7 были выполнены вычисления всех девяти комбинаций из таблицы 1 при помощи программы MS-Excel. Полученные результаты отображены в таблице 2 и 3.
Таблица 2.
Результаты проведённого эксперимента по решению проблем использования фундаментальной шкалы Т. Саати в форме разных модификаций первого поколения для повышения степени универсальности применения МАИ в методике выбора эффективных проектов и др. областях науки за счёт повышения точности измерений, баллы
Table 2.
The results of the experiment conducted to solve the problems of using the T. Saaty fundamental scale in the form of various modifications of the first generation to increase the degree of universality of the use of AHP in the methodology of selecting effective projects and other fields of science by increasing the accuracy of measurements, points
|
Объекты матрицы, млн руб. | Matrix objects, m. rub. |
NPV |
NPV , |
NPV |
NPV |
NPV |
NPV |
Объекты матрицы, млн руб. | Matrix objects, m. rub. |
NPV |
NPV , |
NPV |
NPV |
NPV |
NPV |
∑n i=i |
yk nF! ∑ n ԝ= k |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
FAHPMS-М1.1 / Шкала целочисленная [1; …;9], только 8 основных интервалов измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( ) =NPV ( ) Расширенная транзитивная цепь из ˅ : а =а >а =а =а =а >а =а =а =а =а >а =а >а =а ⇒ ⇒ 9=9>5=5=5=5>4=4=4=4=4>2=2>1=1 Расширенная транзитивная цепь из / ˅ / : а =а >а =а >а =а =а =а =а >а =а =а =а >а =а ⇒ ^ 1=1>0,5000=0,5000>0,2500=0,2500=0,2500=0,2500=0,2500>0,2000=0,2000=0,2000=0,2000>0,1111=0,1111 Транзитивная цепь из w ^ : w “pv e73 > w "pv 3oa > w "pv »7 = w "pV 37 > w "pv2w ,g = w "pv i ^ ⇒ 0,4936 > 0,1879 > 0,1215 = 0,1215 > 0,0378 = 0,0378 |
|||||||||||||||
|
NPV |
1 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV |
0,0417 |
0,0417 |
0,0263 |
0,0263 |
0,0313 |
0,0593 |
0,2266 |
0,0378 |
|
NPV , |
1 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV , |
0,0417 |
0,0417 |
0,0263 |
0,0263 |
0,0313 |
0,0593 |
0,2266 |
0,0378 |
|
NPV |
4 |
4 |
1 |
1 |
0,5000 |
0,2000 |
NPV |
0,1667 |
0,1667 |
0,1053 |
0,1053 |
0,0781 |
0,1068 |
0,7288 |
0,1215 |
|
NPV |
4 |
4 |
1 |
1 |
0,5000 |
0,2000 |
NPV |
0,1667 |
0,1667 |
0,1053 |
0,1053 |
0,0781 |
0,1068 |
0,7288 |
0,1215 |
|
NPV |
5 |
5 |
2 |
2 |
1 |
0,2500 |
NPV |
0,2083 |
0,2083 |
0,2105 |
0,2105 |
0,1563 |
0,1335 |
1,1275 |
0,1879 |
|
NPV |
9 |
9 |
5 |
5 |
4 |
1 |
NPV |
0,3750 |
0,3750 |
0,5263 |
0,5263 |
0,6250 |
0,5341 |
2,9618 |
0,4936 |
|
∑а i=l |
24 |
24 |
9,5 |
9,5 |
6,4 |
1,8722 |
∑n i=l |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.2 / Шкала целочисленная [1; …;9], только 8 основных интервалов измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( , ) =NPV ( ) Расширенная транзитивная цепь из ˅ : а =а >а =а =а =а >а =а =а =а =а >а =а >а >а ⇒ ⇒ 9=9>5=5=5=5>4=4=4=4=4>2=2>1>0 Расширенная транзитивная цепь из / ˅ / : а >а =а >а =а =а =а =а >а =а =а =а >а =а >а ⇒ ^ 1>0,5000=0,5000>0,2500=0,2500=0,2500=0,2500=0,2500>0,2000=0,2000=0,2000=0,2000>0,1111=0,1111>0 Транзитивная цепь из w^: w"pv e73 > w npv S 08 > wNpv i>7 = w npv ^7 > w npv2 10 , 9 = wNpv i ^ ⇒ 0,4761 > 0,2091 > 0,1116 = 0,1116 > 0,0458 = 0,0458 |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
NPV |
0 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV |
0 |
0,0435 |
0,0333 |
0,0333 |
0,0370 |
0,1274 |
0,2746 |
0,0458 |
|
NPV , |
1 |
0 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV , |
0,0435 |
0 |
0,0333 |
0,0333 |
0,0370 |
0,1274 |
0,2746 |
0,0458 |
|
NPV |
4 |
4 |
0 |
0 |
0,5000 |
0,2000 |
NPV |
0,1739 |
0,1739 |
0 |
0 |
0,0926 |
0,2293 |
0,6697 |
0,1116 |
|
NPV |
4 |
4 |
0 |
0 |
0,5000 |
0,2000 |
NPV |
0,1739 |
0,1739 |
0 |
0 |
0,0926 |
0,2293 |
0,6697 |
0,1116 |
|
NPV |
5 |
5 |
2 |
2 |
0 |
0,2500 |
NPV |
0,2174 |
0,2174 |
0,2667 |
0,2667 |
0 |
0,2866 |
1,2547 |
0,2091 |
|
NPV |
9 |
9 |
5 |
5 |
4 |
0 |
NPV |
0,3913 |
0,3913 |
0,6667 |
0,6667 |
0,7407 |
0 |
2,8567 |
0,4761 |
|
∑ а |
23 |
23 |
7,5 |
7,5 |
5,4 |
0,8722 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.3 / Шкала целочисленная [1; …;9],только 8 основных интервалов измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( ) =NPV ( ) Расширенная транзитивная цепь из ˅ : а =а >а =а =а =а >а =а =а =а =а >а =а >а >а ⇒ ⇒9=9>5=5=5=5>4=4=4=4=4>2=2>1>0 Расширенная транзитивная цепь из / ˅ / : а >а =а >а =а =а =а =а >а =а =а =а >а =а >а ⇒ ^ 1 > 0,5000 = 0,5000 > 0,2500 = 0,2500 = 0,2500 = 0,2500 = 0,2500 > 0,2000 = 0,2000 = 0,2000 = 0,2000 > 0,1111 = 0,1111 > 0 Транзитивная цепь из w ^ : w"pv s > w"pv s > w"pV 4? = w"pv ^_ > w"pV 2Qg = w"pv i ^ 0,5143 > 0,1962 > 0,1060 = 0,1060 > 0,0388 = 0,0388 |
|||||||||||||||
|
NPV |
1 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV |
0,0417 |
0,0417 |
0,0294 |
0,0294 |
0,0313 |
0,0593 |
0,2328 |
0,0388 |
|
NPV , |
1 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV , |
0,0417 |
0,0417 |
0,0294 |
0,0294 |
0,0313 |
0,0593 |
0,2328 |
0,0388 |
|
NPV |
4 |
4 |
1 |
0 |
0,5000 |
0,2000 |
NPV |
0,1667 |
0,1667 |
0,1176 |
0 |
0,0781 |
0,1068 |
0,6359 |
0,1060 |
|
NPV |
4 |
4 |
0 |
1 |
0,5000 |
0,2000 |
NPV |
0,1667 |
0,1667 |
0 |
0,1176 |
0,0781 |
0,1068 |
0,6359 |
0,1060 |
|
NPV |
5 |
5 |
2 |
2 |
1 |
0,2500 |
NPV |
0,2083 |
0,2083 |
0,2353 |
0,2353 |
0,1563 |
0,1335 |
1,1770 |
0,1962 |
|
NPV |
9 |
9 |
5 |
5 |
4 |
1 |
NPV |
0,3750 |
0,3750 |
0,5882 |
0,5882 |
0,6250 |
0,5341 |
3,0856 |
0,5143 |
|
∑ а |
24 |
24 |
8,5 |
8,5 |
6,4 |
1,8722 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.4 / Шкала целочисленная [1; …;9], только 8 основных интервалов измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( , ) =NPV ( ) Расширенная транзитивная цепь из ˅ : а =а >а =а =а =а >а =а =а =а =а >а =а >а =а ⇒ ⇒ 9=9>5=5=5=5>4=4=4=4=4>2=2>1=1 Расширенная транзитивная цепь из / ˅ / : а =а >а =а >а =а =а =а =а >а =а =а =а >а =а ⇒ ^ 1=1>0,5000=0,5000>0,2500=0,2500=0,2500=0,2500=0,2500>0,2000=0,2000=0,2000=0,2000>0,1111=0,1111 Транзитивная цепь из w^: w " pv e > w " PV 3 > w " PV4 = w " PV 3 > w “PV 2 = w " PV 1 ^ , ⇒ 0,4500 > 0,1987 > 0,1312 = 0,1312 > 0,0445 = 0,0445 |
|||||||||||||||
|
NPV |
0 |
1 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV |
0 |
0,0435 |
0,0294 |
0,0294 |
0,0370 |
0,1274 |
0,2667 |
0,0445 |
|
NPV , |
1 |
0 |
0,2500 |
0,2500 |
0,2000 |
0,1111 |
NPV , |
0,0435 |
0 |
0,0294 |
0,0294 |
0,0370 |
0,1274 |
0,2667 |
0,0445 |
|
NPV |
4 |
4 |
0 |
1 |
0,5000 |
0,2000 |
NPV |
0,1739 |
0,1739 |
0 |
0,1176 |
0,0926 |
0,2293 |
0,7874 |
0,1312 |
|
NPV |
4 |
4 |
1 |
0 |
0,5000 |
0,2000 |
NPV |
0,1739 |
0,1739 |
0,1176 |
0 |
0,0926 |
0,2293 |
0,7874 |
0,1312 |
|
NPV |
5 |
5 |
2 |
2 |
0 |
0,2500 |
NPV |
0,2174 |
0,2174 |
0,2353 |
0,2353 |
0 |
0,2866 |
1,1920 |
0,1987 |
|
NPV |
9 |
9 |
5 |
5 |
4 |
0 |
NPV |
0,3913 |
0,3913 |
0,5882 |
0,5882 |
0,7407 |
0 |
2,6998 |
0,4500 |
|
∑ а |
23 |
23 |
8,5 |
8,5 |
5,4 |
0,8722 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
FAHPMS-М1.5 / Шкала дробночисленная [1; …;9] в 8 основных интервалах измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ()>NPV ()>NPV ()=NPV ()>NPV ()>NPV () Расширенная транзитивная цепь из ˅ : а >а >а >а >а =а >а =а >а =а >а >а =а >а =а ⇒ ⇒9>8,8418>5,4545>5,2964>5,2364=5,2364>3,7636=3,7636>3,6055=3,6055>3,5455>1,6909=1,6909>1=1 Расширенная транзитивная цепь из / ˅ / : а =а >а =а >а >а =а >а =а >а =а >а >а >а >а ⇒ ^ 1 = 1 > 0,5914 = 0,5914 > 0,2821 > 0,2774 = 0,2774 > 0,2657 = 0,2657 > 0,1910 = 0,1910 > 0,1888 > 0,1833 > 0,1131 > 0,1111 Транзитивная цепь из w ^ : w”pV 6 > w"pv s > w"PV 47 = w"PV 37 > w"pV 2Qg > w”pv i ^ 0,4951 > 0,1874 > 0,1201 = 0,1201 > 0,0390 > 0,0383 |
|||||||||||||||
|
NPV |
1 |
1 |
0,2657 |
0,2657 |
0,1833 |
0,1111 |
NPV |
0,0417 |
0,0428 |
0,0281 |
0,0281 |
0,0301 |
0,0588 |
0,2295 |
0,0383 |
|
NPV , |
1 |
1 |
0,2774 |
0,2774 |
0,1888 |
0,1131 |
NPV , |
0,0417 |
0,0428 |
0,0293 |
0,0293 |
0,0310 |
0,0599 |
0,2339 |
0,0390 |
|
NPV |
3,7636 |
3,6055 |
1 |
1 |
0,5914 |
0,1910 |
NPV |
0,1569 |
0,1544 |
0,1056 |
0,1056 |
0,0969 |
0,1011 |
0,7206 |
0,1201 |
|
NPV |
3,7636 |
3,6055 |
1 |
1 |
0,5914 |
0,1910 |
NPV |
0,1569 |
0,1544 |
0,1056 |
0,1056 |
0,0969 |
0,1011 |
0,7206 |
0,1201 |
|
NPV |
5,4545 |
5,2964 |
1,6909 |
1,6909 |
1 |
0,2821 |
NPV |
0,2274 |
0,2268 |
0,1785 |
0,1785 |
0,1639 |
0,1494 |
1,1247 |
0,1874 |
|
NPV |
9 |
8,8418 |
5,2364 |
5,2364 |
3,5455 |
1 |
NPV |
0,3753 |
0,3787 |
0,5529 |
0,5529 |
0,5812 |
0,5296 |
2,9706 |
0,4951 |
|
∑ а |
23,9818 |
23,3491 |
9,4703 |
9,4703 |
6,1004 |
1,8882 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.6 / Шкала дробночисленная [1; …;9] в 8 основных интервалах измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ()>NPV ()>NPV ()=NPV ()>NPV ()>NPV () Расширенная транзитивная цепь из ˅ : а >а >а >а >а =а >а =а >а =а >а >а =а >а >а ⇒ ⇒9>8,8418>5,4545>5,2964>5,2364=5,2364>3,7636=3,7636>3,6055=3,6055>3,5455>1,6909=1,6909>1>0 Расширенная транзитивная цепь из / ˅ / : а >а =а >а >а =а >а =а >а =а >а >а >а >а >а ⇒ ^ 1 > 0,5914 = 0,5914 > 0,2821 > 0,2774 = 0,2774 > 0,2657 = 0,2657 > 0,1910 = 0,1910 > 0,1888 > 0,1833 > 0,1131 > 0,1111 > 0 Транзитивная цепь из w£i: w “pv e73 > w "pv 3oa > w "pv4 7 = w "pV 37 > w npv 20 , 9 > w "pv i ^ ⇒ 0,4807 > 0,2074 > 0,1093 = 0,1093 > 0,0470 > 0,0462 |
|||||||||||||||
|
NPV |
0 |
1 |
0,2657 |
0,2657 |
0,1833 |
0,1111 |
NPV |
0 |
0,0447 |
0,0356 |
0,0356 |
0,0359 |
0,1251 |
0,2769 |
0,0462 |
|
NPV , |
1 |
0 |
0,2774 |
0,2774 |
0,1888 |
0,1131 |
NPV , |
0,0435 |
0 |
0,0371 |
0,0371 |
0,0370 |
0,1273 |
0,2821 |
0,0470 |
|
NPV |
3,7636 |
3,6055 |
0 |
0 |
0,5914 |
0,1910 |
NPV |
0,1638 |
0,1613 |
0 |
0 |
0,1160 |
0,2150 |
0,6561 |
0,1093 |
|
NPV |
3,7636 |
3,6055 |
0 |
0 |
0,5914 |
0,1910 |
NPV |
0,1638 |
0,1613 |
0 |
0 |
0,1160 |
0,2150 |
0,6561 |
0,1093 |
|
NPV |
5,4545 |
5,2964 |
1,6909 |
1,6909 |
0 |
0,2821 |
NPV |
0,2373 |
0,2370 |
0,2263 |
0,2263 |
0 |
0,3176 |
1,2446 |
0,2074 |
|
NPV |
9 |
8,8418 |
5,2364 |
5,2364 |
3,5455 |
0 |
NPV |
0,3916 |
0,3956 |
0,7010 |
0,7010 |
0,6951 |
0 |
2,8843 |
0,4807 |
|
∑ а |
22,9818 |
22,3491 |
7,4703 |
7,4703 |
5,1004 |
0,8882 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.7 / Шкала дробночисленная [1; …;9] в 8 основных интервалах измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ()>NPV ()>NPV ()=NPV ()>NPV ()>NPV () Расширенная транзитивная цепь из ˅ : а >а >а >а >а =а >а =а >а =а >а >а =а >а >а ⇒ ⇒ 9>8,8418>5,4545>5,2964>5,2364=5,2364>3,7636=3,7636>3,6055=3,6055>3,5455>1,6909=1,6909>1>0 Расширенная транзитивная цепь из / ˅ / : а >а =а >а >а =а >а =а >а =а >а >а >а >а >а ⇒ ^ 1>0,5914=0,5914>0,2821>0,2774=0,2774>0,2657=0,2657>0,1910=0,1910>0,1888>0,1833>0,1131>0,1111>0 Транзитивная цепь из w ^ : w”pV 6 > w"pv s > w"PV 47 = w”pV 37 > w"pV 2Qg > w"pv i ^ 0,5169 > 0,1945 > 0,1046 = 0,1046 > 0,0401 > 0,0394 |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
NPV |
1 |
1 |
0,2657 |
0,2657 |
0,1833 |
0,1111 |
NPV |
0,0417 |
0,0428 |
0,0314 |
0,0314 |
0,0301 |
0,0588 |
0,2362 |
0,0394 |
|
NPV , |
1 |
1 |
0,2774 |
0,2774 |
0,1888 |
0,1131 |
NPV , |
0,0417 |
0,0428 |
0,0327 |
0,0327 |
0,0310 |
0,0599 |
0,2409 |
0,0401 |
|
NPV |
3,7636 |
3,6055 |
1 |
0 |
0,5914 |
0,1910 |
NPV |
0,1569 |
0,1544 |
0,1181 |
0 |
0,0969 |
0,1011 |
0,6275 |
0,1046 |
|
NPV |
3,7636 |
3,6055 |
0 |
1 |
0,5914 |
0,1910 |
NPV |
0,1569 |
0,1544 |
0 |
0,1181 |
0,0969 |
0,1011 |
0,6275 |
0,1046 |
|
NPV |
5,4545 |
5,2964 |
1,6909 |
1,6909 |
1 |
0,2821 |
NPV |
0,2274 |
0,2268 |
0,1996 |
0,1996 |
0,1639 |
0,1494 |
1,1668 |
0,1945 |
|
NPV |
9 |
8,8418 |
5,2364 |
5,2364 |
3,5455 |
1 |
NPV |
0,3753 |
0,3787 |
0,6182 |
0,6182 |
0,5812 |
0,5296 |
3,1012 |
0,5169 |
|
∑ а |
23,9818 |
23,3491 |
8,4703 |
8,4703 |
6,1004 |
1,8882 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.8 / Шкала дробночисленная [1; …;9] в 8 основных интервалах измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( ) >NPV ( ) Расширенная транзитивная цепь из ˅ : а >а >а >а >а =а >а =а >а =а >а >а =а >а >а ⇒ ⇒ 9>8,8418>5,4545>5,2964>5,2364=5,2364>3,7636=3,7636>3,6055=3,6055>3,5455>1,6909=1,6909>1=1 Расширенная транзитивная цепь из / ˅ / : а >а >а =а >а >а =а >а =а >а =а >а >а >а >а ⇒ ^ 1=1>0,5914=0,5914>0,2821>0,2774=0,2774>0,2657=0,2657>0,1910=0,1910>0,1888>0,1833>0,1131>0,1111 Транзитивная цепь из w £j : w " |?v v > w "pv s08 > w "PV 4 7 = < р^ 7 > w npv2 0 , 9 > w "pv i ^ ^ 0,4531 > 0,1985 > 0,1290 = 0,1290 > 0,0456 > 0,0448 |
|||||||||||||||
|
NPV |
0 |
1 |
0,2657 |
0,2657 |
0,1833 |
0,1111 |
NPV |
0 |
0,0447 |
0,0314 |
0,0314 |
0,0359 |
0,1251 |
0,2685 |
0,0448 |
|
NPV , |
1 |
0 |
0,2774 |
0,2774 |
0,1888 |
0,1131 |
NPV , |
0,0435 |
0 |
0,0327 |
0,0327 |
0,0370 |
0,1273 |
0,2734 |
0,0456 |
|
NPV |
3,7636 |
3,6055 |
0 |
1 |
0,5914 |
0,1910 |
NPV |
0,1638 |
0,1613 |
0 |
0,1181 |
0,1160 |
0,2150 |
0,7741 |
0,1290 |
|
NPV |
3,7636 |
3,6055 |
1 |
0 |
0,5914 |
0,1910 |
NPV |
0,1638 |
0,1613 |
0,1181 |
0 |
0,1160 |
0,2150 |
0,7741 |
0,1290 |
|
NPV |
5,4545 |
5,2964 |
1,6909 |
1,6909 |
0 |
0,2821 |
NPV |
0,2373 |
0,2370 |
0,1996 |
0,1996 |
0 |
0,3176 |
1,1911 |
0,1985 |
|
NPV |
9 |
8,8418 |
5,2364 |
5,2364 |
3,5455 |
0 |
NPV |
0,3916 |
0,3956 |
0,6182 |
0,6182 |
0,6951 |
0 |
2,7188 |
0,4531 |
|
∑ а |
22,9818 |
22,3491 |
8,4703 |
8,4703 |
5,1004 |
0,8882 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
|
FAHPMS-М1.9 / Шкала дробночисленная [0; …;9]+1в 9 основных интервалах измерения / = ⇒ = / = ⇒ = Транзитивная цепь из (): NPV ( ) >NPV ( ) >NPV ( ) =NPV ( ) >NPV ( ) >NPV ( ) Расширенная транзитивная цепь из ˅ : а >а >а >а >а =а >а =а >а =а >а >а =а >а >а ⇒ ⇒ 9>8,8594>5,8485>5,7079>5,6545=5,6545>4,3455=4,3455>4,2048=4,2048>4,1515>2,5030=2,5030>1,1406>1 Расширенная транзитивная цепь из / ˅ / : а >а >а =а >а >а =а >а =а >а =а >а >а >а >а ⇒ ^ 1>0,8767>0,3995=0,3995>0,2409>0,2378=0,2378>0,2301=0,2301>0,1768=0,1768>0,1752>0,1710>0,1129>0,1111 Транзитивная цепь из wi: w"pv e73 > w"pv =oa > w"pv i>7 = w"pv ^7 > w"pv2 10,g > wNPv a ^ ^ 0,4967 > 0,2033 > 0,1146 = 0,1146 > 0,0366 > 0,0343 |
|||||||||||||||
|
NPV |
1 |
0,8767 |
0,2301 |
0,2301 |
0,1710 |
0,1111 |
NPV |
0,0389 |
0,0353 |
0,0217 |
0,0217 |
0,0272 |
0,0611 |
0,2058 |
0,0343 |
|
NPV , |
1,1406 |
1 |
0,2378 |
0,2378 |
0,1752 |
0,1129 |
NPV , |
0,0444 |
0,0402 |
0,0224 |
0,0224 |
0,0278 |
0,0621 |
0,2193 |
0,0366 |
|
NPV |
4,3455 |
4,2048 |
1 |
1 |
0,3995 |
0,1768 |
NPV |
0,1692 |
0,1692 |
0,0941 |
0,0941 |
0,0634 |
0,0972 |
0,6873 |
0,1146 |
|
NPV |
4,3455 |
4,2048 |
1 |
1 |
0,3995 |
0,1768 |
NPV |
0,1692 |
0,1692 |
0,0941 |
0,0941 |
0,0634 |
0,0972 |
0,6873 |
0,1146 |
|
NPV |
5,8485 |
5,7079 |
2,5030 |
2,5030 |
1 |
0,2409 |
NPV |
0,2277 |
0,2297 |
0,2356 |
0,2356 |
0,1588 |
0,1325 |
1,2198 |
0,2033 |
|
NPV |
9 |
8,8594 |
5,6545 |
5,6545 |
4,1515 |
1 |
NPV |
0,3505 |
0,3565 |
0,5322 |
0,5322 |
0,6593 |
0,5499 |
2,9805 |
0,4967 |
|
∑ а |
25,6800 |
24,8537 |
10,6255 |
10,6255 |
6,2967 |
1,8186 |
∑ n |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
Таблица 3. Сравнение полученных результатов проведённого эксперимента по решению проблем использования фундаментальной шкалы Т. Саати в форме разных модификаций первого поколения для повышения степени универсальности применения МАИ в методике выбора эффективных проектов и др. областях науки за счёт повышения точности измерений
Table 3. Comparison of the obtained results of the experiment conducted to solve the problems of using the T. Saaty fundamental scale in the form of various modifications of the first generation to increase the degree of universality of the use of AHP in the methodology of selecting effective projects and other fields of science by increasing the accuracy of measurements
|
Варианты шкал оценивания для методики и МАИ Variants of assessment scales for the methodology and AHP |
Классификаторы и условия Classifiers and conditions |
Объекты матрицы парных сравнений из иерархии решения проблемы выбора эффективных проектов, млн руб. | Objects of the matrix of paired comparisons from the hierarchy of solving the problem of choosing effective projects, m. rub. |
|||||
|
A1(1) NPV ’ (1 ) |
A2(2) NPV2(2 ) NPV , |
A3(3) NPV3(3 ) |
A4(4) NPV T (4) |
A5(5) NPV5(5 ) NPV |
A6(6) NPV г ( 3) |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Целочисленная [1; …;9] только 8 основных интервалов измерения | Integer [1; ...;9] only 8 main measurement intervals |
FAHPMS-М1.1 Ai(j) = Aj(i) ⇒ а$=1; Ai(j) =Aj(i) ⇒аij =1 |
Ml.1 ԝ .: |
|||||
|
0,0378 |
0,0378 |
0,1215 |
0,1215 |
0,1879 |
0,4936 |
||
|
∑i=l |ΔwAi'.1|=0, 0370, слагаемые: |
|||||||
|
0,0035 |
0,0012 |
0,0069 |
0,0069 |
0,0154 |
0,0031 |
||
|
λ =6,2472 |
|||||||
|
CI =0,0494 |
|||||||
|
CR(0,0399) < 0,1, удовлетворяет неравенство |
|||||||
|
FAHPMS-М1.2 Ai(j) = Aj(i) ⇒ а 5=0; Ai(j) =Aj(i) ⇒аIj =0 |
Ml.2. ԝ . : |
||||||
|
0,0458 |
0,0458 |
0,1116 |
0,1116 |
0,2091 |
0,4761 |
||
|
∑i=l |ΔwAi'.2|=0, 0530, слагаемые: |
|||||||
|
0,0115 |
0,0092 |
0,0029 |
0,0029 |
0,0058 |
0,0206 |
||
|
λ =5,3239 |
|||||||
|
CI = -0,1352 |
|||||||
|
CR(-0,1091) < 0,1, удовлетворяет неравенство |
|||||||
|
FAHPMS-М1.3 Ai(j) = Aj(i) ⇒ а$=1; Ai(j) =Aj(i) ⇒аij =0 |
Ml.3. ԝ .: |
||||||
|
0,0388 |
0,0388 |
0,1060 |
0,1060 |
0,1962 |
0,5143 |
||
|
∑i=l |ΔwAi'.3|=0, 0485, слагаемые: |
|||||||
|
0,0045 |
0,0022 |
0,0086 |
0,0086 |
0,0071 |
0,00175 |
||
|
λ = 5,8822 |
|||||||
|
CI = -0,0236 |
|||||||
|
CR(-0,0190) < 0,1, удовлетворяет неравенство |
|||||||
|
FAHPMS-М1.4 Ai(j) = Aj(i) ⇒ а 5=0; Ai(j) =Aj(i) ⇒аij =1 |
Ml.4. ԝ .: |
||||||
|
0,0445 |
0,0445 |
0,1312 |
0,1312 |
0,1987 |
0,4500 |
||
|
∑i=l |ΔwAi'.4|=0, 1028, слагаемые: |
|||||||
|
0,0102 |
0,0079 |
0,0167 |
0,0167 |
0,0046 |
0,0468 |
||
|
λ =5,7410 |
|||||||
|
CI = -0,0518 |
|||||||
|
CR(-0,0418) < 0,1, удовлетворяет неравенство |
|||||||
|
Дробночисленная [1; …;9] в 8 основных интервалах измерения | Fractional [1; ...;9] in 8 main measurement intervals |
FAHPMS-М1.5 Ai(j) = Aj(i) ⇒ а 5=1; Ai(j) =Aj(i) ⇒аij =1 |
Ml.5. ԝ . : |
|||||
|
0,0383 |
0,0390 |
0,1201 |
0,1201 |
0,1874 |
0,4951 |
||
|
∑i=l |ΔWAi1 .5|=0, 0350, слагаемые: |
|||||||
|
0,0040 |
0,0024 |
0,0056 |
0,0056 |
0,0159 |
0,0016 |
||
|
λ = 6,181 |
|||||||
|
CI = 0,0362 |
|||||||
|
CR(0,0292) < 0,1, удовлетворяет неравенство |
|||||||
|
FAHPMS-М1.6 Ai(j) = Aj(i) ⇒ а 5=0; Ai(j) =Aj(i) ⇒аij =0 |
Ml.6. ԝ . : |
||||||
|
0,0462 |
0,0470 |
0,1093 |
0,1093 |
0,2074 |
0,4807 |
||
|
∑i = 1 |Δw^1.6|=0, 0529, слагаемые: |
|||||||
|
0,0119 |
0,0105 |
0,0052 |
0,0052 |
0,0041 |
0,0160 |
||
|
λ = 5,2301 |
|||||||
|
CI = -0,154 |
|||||||
|
CR(-0,1242) < 0,1, удовлетворяет неравенство |
|||||||
Продолжение табл. 3 | Continuation of table 3 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
FAHPMS-М1.7 Ai(j) = Aj(i) ⇒ а =1; Ai(j) =Aj(i) ⇒а =0 |
. ԝ : |
||||||
|
0,0394 |
0,0401 |
0,1046 |
0,1046 |
0,1945 |
0,5169 |
||
|
∑ |Δ . | = , , слагаемые: |
|||||||
|
0,0051 |
0,0036 |
0,0100 |
0,0100 |
0,0088 |
0,0201 |
||
|
λ = 5,8152 |
|||||||
|
CI = -0,0370 |
|||||||
|
CR(-0,0298) < 0,1, удовлетворяет неравенство |
|||||||
|
FAHPMS-М1.8 Ai(j) = Aj(i) ⇒ а = 0; Ai(j) = Aj(i) ⇒ а = 1 |
. ԝ : |
||||||
|
0,0448 |
0,0456 |
0,1290 |
0,1290 |
0,1985 |
0,4531 |
||
|
∑ |Δ . | = , , слагаемые: |
|||||||
|
0,0105 |
0,0090 |
0,0145 |
0,0145 |
0,0048 |
0,0436 |
||
|
λ = 5,6474 |
|||||||
|
CI = -0,0705 |
|||||||
|
CR(-0,0569) < 0,1, удовлетворяет неравенство |
|||||||
|
Дробночисленная [0; …;8]+1 в 8 основных интервалах измерения | Fractional [0; ...;8]+1 in 8 main measurement intervals |
FAHPMS-М1.9 Ai(j) = Aj(i) ⇒ а = 0+1=1; Ai(j) = Aj(i) ⇒ а = 0+1=1 |
. ԝ : |
|||||
|
0,0343 |
0,0366 |
0,1146 |
0,1146 |
0,2033 |
0,4967 |
||
|
ԝ . является базой для вычисления Δԝ . |
|||||||
|
λ = 6,4071 |
|||||||
|
CI = 0,0814 |
|||||||
|
CR(0,0657) < 0,1, удовлетворяет неравенство |
|||||||
|
Абсолютные отклонения локальных векторов 8-ми комбинаций по отношению к локальному вектору комбинации 9, по каждому объекту Ai(j) | Absolute deviations of local vectors of 8 combinations with respect to the local vector of combination 9, for each object Ai(j) |
. . . ∑ | ∑ Δ | |
= , , слагаемые: |
|||||
|
NPV ( ) |
() NPV , |
NPV ( ) |
NPV ( ) |
() NPV |
NPV ( ) |
||
|
0,0609 |
0,0461 |
0,0703 |
0,0703 |
0,0666 |
0,1694 |
||
|
Абсолютные отклонения локальных векторов 8-ми комбинаций по отношению к локальному вектору комбинации 9, по каждой модификации М1.N ∑ . |∑ Δ . | = , , слагаемые: * N=const * |
|||||||
|
М1.1 |
М1.2 |
М1.3 |
М1.4 |
М1.5 |
М1.6 |
М1.7 |
М1.8 |
|
0,0370 |
0,0530 |
0,0485 |
0,1028 |
0,0350 |
0,0529 |
0,0575 |
0,0968 |
Примечание к таблице 3. Важно отметить, что указанные экспериментальные данные в большей степени ориентированы на классификатор FAHPMS-М1.N. Однако полученные результаты эксперимента будут вполне справедливы по отношению к классификаторам AHPMS(AM)-М1.N и AHPDD-М1.N, т.к. вычисление матричных оценок по формуле 1 и 2 осуществляется стандартно для всех указанных классификаторов с учётом трёх нестандартных случаев [11] в границах целочисленной [1; …;9] и дробночисленных шкал [1; …;9] или [0; …; 8] + 1. Отличие заключается лишь в источниках, уровня доверия, определённости и др. характеристик данных измерения объектов иерархии в матрицах. Что касается классификатора AHPMS-М1.N, то он отличается от остальных трёх тем, что обладает свойствами низкой точности измерений из за явно выраженного фактора субъективизма, полной или частичной неопределённости измерений данных, полным или частичным отсутствием какой-либо связи с измерителями и измерениями объектов в матрице иерархии и т.д. (таблица 4 из ист. [11]).
При этом оценивание в AHPMS-М1.N эксперты производят напрямую в ячейках матрицы согласно шкале и двум условиям, принадлежащих той или иной комбинации из девяти предложенных, минуя формулу 1(2) и её приложения. Поэтому полученные результаты эксперимента будут тоже справедливы по отношению к AHPMS-М1.N тоже.
Обсуждение результатов
После того, как все девять комбинаций просчитаны опишем резервы роста точности измерений локальных векторов приоритетов с учётом ранее сформулированных решений пяти проблем [11]. Это позволит нам выбрать и утвердить эталон эксперимента для практики использования МАИ в разных областях науки и в методике выбора эффективных проектов в том числе.
Эталоном измерения векторных оценок будем считать ту модификацию (комбинацию), которая в большей степени будет отвечать требованиям высокой точности измерений по результату реализованного анализа экспериментальных данных.
Для корректного использования формулы 1(2) следует выполнять несколько обязательных правил [11], которые позволят максимально эффективно использования резервы роста точности измерений.
Первое правило для использования формулы 1 и 2. Все объекты матрицы парных сравнений должны быть привязаны к единым или смежным измерителям и к единым измерениям в чётком («жёстко» детерминированные данные) или нечётком выражении, условно искусственного или условно естественного характера. Если в матрице присутствуют объекты, которые не соответствуют указанному правилу, то их следует: постараться измерить в единых единицах измерения при помощи каких-либо единых или смежных измерителей; применить другие единые или смежные единицы измерения, пригодные для всех объектов матрицы парных сравнений; в крайнем случае заменить на смежный объект или вовсе исключить из матрицы. Если указанное правило не соблюдается, то эксперт (-ты) будут вынуждены использовать классификаторы AHP-MO.O(N) или AHPMS-M1.N (таблица 4). При этом дробночисленные шкалы [1; ,.;9] и [0; ,.;8]+1 вполне могут стать альтернативой целочисленной шкале [1; ..;9]. Просто эксперты будут реализовывать оценивание традиционно - попарно в ячейках матрицы, как завещал Т. Саати.
Второе правило для использования формулы 1. В случае применения целочисленной шкалы [1; ^;9] все значения, вычисленные по формуле 1 округляются по правилам математики до целых чисел, но если соблюдается условие (а ˅ а ) < 1, то всегда до единицы. Для дробночисленной шкалы [1; ^;9] при обнаружении условия (а^ v а -- ) < 1 округление делается всегда до единицы.
Указанные основные и др. [11] условия для использования резервов роста точности измерений для модификаций МАИ первого поколения в эксперименте выполнены.
Резерв 1. Рост точности измерений за счёт введения дробночисленных измерений а ˅ а , которые получены при помощи формулы 1 и 2. Это решение позволит не только повысить точность измерений а ˅ а , но и использовать условно неограниченное число объектов Аi(j) в матрице парных сравнений. Что способствовало введению новых категорий: «Суперзадача» (Super Task); «Суперматрица» (Super Matrix); «Супериерархия» (Super Hierarchy); «Супермассив Данных» (Super Data Array) [11].
Эти категории будут дополнительно раскрыты и в др. статьях автора. Кроме того, дробночисленное измерение позволяет делать «тонкие» различия между примерно равными сравниваемыми объектами или между объектами, отличающимися в разы, десяти, сто и более кратном измерении. Поэтому резерв 1 очень важен, особенно когда решается проблема распределения инвестиционного денежного потока или другого ограниченного ресурса по проектам и не только.
Резерв 1 использован в модификациях первого поколения М1.5–9, при этом более точные измерения находятся в диапазоне [0; . .;8]+1, а не [1; .;9]. В случаях М1.1-4 присутствуют неточные или даже «очень грубые» измерения а ˅ а , безразличные к тонким параметрам из-за целочисленной шкалы [1; .;9]. А для М1.5–М1.8 свойственна грубая ошибка измерений матричных оценок, т.к. применяется обязательное второе правило. Без этого правила в случаях (а v а ) < 1 можно получить алогизм [11], который повлечёт за собой очень грубые искажения и даже ошибки в вычислениях. Поэтому забегая вперёд отметим в качестве эталона измерений модифицированного МАИ в первом поколении комбинацию М.1.9. Далее результаты анализа экспериментальных данных это подтвердят.
Указанные неточности особенно очень грубые не могут быть допущены в науке математика, которая стремится к точным измерениям в разных проявлениях, даже если и МАИ считается нечётким измерителем экспертных суждений в решении задач многокритериального выбора. Да и вообще имеет ли научноматематический смысл классическая форма МАИ, которая работает с объектами иерархии Аi, не привязанными к единым измерениям и измерителям или всё же требуются решения, обладающие новизной и полезные для теории и практики в разных областях науки? На этот вопрос автор отвечает в данной и в уже опубликованной статье [11], где модифицируется МАИ, а также продолжит это делать в будущем.
Например для комбинаций М1.5–М1.8 и М1.9 матричная оценка а была вычислена по формуле 1 и 2, следующим образом:
| , | [ ;…; ],М .
а 21 ((173-8)/9) 0,1582 1 6 [1;_;9],М1.5-8 ,
- ;7" ? ■ । i/-^ 0 . 8 ■
1,М1.9.
Для комбинаций М1.1 — 4 значение а 21 = 1 балл и для М1.5 — 8 значение а 21 = 1 балл т.к. применялось правило 2, которое требует округления до единицы во всех случаях в которых соблюдается неравенство типа -
Шагеев Д.А. Вестник ВГУИТ, 2022, Т. 84, №. 1, С. 388-409 (а ij ˅ а JJ) < 1. Что касается М1.9, то согласно вычислению по формуле 2 – а21 принято в размере 1,1406 балла. Обратная оценка вычислялась по стандартному правилу МАИ – а 12 = 1/а21, баллы: 1/1=1; 1/1,1406=0,8767.
Другие матричные оценки вычислялись по аналогии с учётом указанных правил, условий и др. инструкций.
Резерв 2. Резервы роста точности измерений заключаются в реализации двух принятых условий [11], при которых Ai(j) = Aj(i) ⇒ а ij ˅ а JJ=0 ˅ 1 ⇒ а5 =0 ˅ 1 и аjjd =0 ˅ 1 в различных сочетаниях.
Первое условие au = оказывает негативное влияние на точность измерений а ■j и ∑ i=l а JJ , далее на njj , потом на ∑j 1njj и в завершении на ԝ Ai =∑j njj /k согласно полученным экспериментальным данным в таблице 2 и 3. При этом негативное влияние есть ничто иное, как «симметричное» искажение точности измерений промежуточных показателей и конечных векторных величин.
Например, в М1.6, где аij =0 и аij =0 ⇒ ∑k-1 а JJ по столбцам Aj: 22,9818; 22,3491;
7,4703; 7,4703; 5,1004; 0,8882. А в М1.7, где а■■ =1 и аij =0 ⇒ ∑i=l аJj по столбцам Aj: 23,9818; 23,3491; 8,4703; 8,4703; 6,1004; 1,8882. Очевидно, разница в «1». Соответственно в М1.7 появились дополнительные измерения в форме njj за счёт других nJj т.к. операция нормирования – n ij =аij/∑^=1 а ij и ԝ Ai =∑j^i n [j /k даёт «1» для ∑i=l n Jj=1 и ∑i=l ԝ Ai = 1, то получаются искажённо измеренные данные: 0,0401; 0,1046; 0,1046; 0,1945; 0,5169.
Второе условие а ij = 1 оказывает «асимметричное» негативное влияние на суммы столбцов, к которым они принадлежат ∑ i=l аJj , далее на их nJj , потом на все ∑j — n Jj и в завершении на все ԝ Ai =∑j —y n Jj /k, согласно полученным экспериментальным данным в таблице 2 и 3.
Например, в М1.6, где аij =0 и аij =0 ⇒ ∑ ■Li а JJ по столбцам Aj: 22,9818; 22,3491;
7,4703; 7,4703; 5,1004; 0,8882. А в М1.8, где а ■J =0 и аij =1 ⇒ ∑i=l а JJ по столбцам Aj: 22,9818; 22,3491; 8,4703; 8,4703; 5,1004;
0,8882. Очевидно, разница в «1» для объектов А3 и А4. Соответственно в М1.8 появились дополнительные измерения в форме n ij для А3 и А4 за счёт других nJJ по их столбцам, т.к. операция нормирования nJJ =аJJ/∑i=l а JJ по их столбцам в границах «1»: n43=1/8,4703=0,1181; n34=1/8,4703=0,1181.
В описанных случаях для М1.7 и М1.8 в конечном счёте можно наблюдать неточность измерения локальных векторов приоритетов. Появление хотя бы одной диагональной или не диагональной «1» влияет на размер всех векторных оценок т.к. соблюдаются условия ∑ i=l ԝ Ai = 1 через нормирование. При этом, чем меньше размер матрицы и разница между сравниваемыми объектами, тем больше искажений привносит эта «1». Похожие искажения измерений можно наблюдать в М1.5 т.к. там соблюдаются следующие условия: i(j) = = Aj(i) ⇒ аij = 1; Ai(j) = Aj(i) ⇒ аij =1.
Указанный резерв 2 в полной мере можно использовать в модификации М1.9, где соблюдаются условия а ■J =0 и аJJ = 0. При этом +1 в М1.9 не окажет влияния на точность измерений, т.к. операция +1 реализуется для всех матричных оценок а ij ˅ а JJ (только не для 1/аij ˅ 1/аJJ .) и только после этого вычисляются их обратные значения 1/аij ˅ 1/аJJ . Комбинации М1.2 и М1.6 даже при соблюдении указанных условий содержат значимые неточности и ошибки в измерениях матричных оценок и не только (таблица 4). Поэтому, даже при частичном или полном использовании резерва 2 их следует отклонить по следующим основным причинам: М1.2 очень низкая точность измерений т.к. шкала целочисленная [1; …;9], а показатель CR(ОС) со знаком «минус»; М1.6 если в некоторых ячейках матричная оценка удовлетворяет неравенство (аij ˅ а JJ) < 1, то согласно введённому правилу 2 следует производить округления до «1», также показатель CR(ОС) со знаком «минус».
Резерв 3. Резервы роста точности измерений за счёт достижения максимально возможной согласованности матричных оценок, выраженных не только через показатель ОС, но и в первую очередь за счёт новых форм построения транзитивных цепей.
Показатель ОС адекватен только для индивидуальных (не для агрегированных.) матричных оценок экспертов полученных при помощи комбинаций AHPMS(AM)-М1.N и FAHPMS-М1.N. ОС адекватен и в случае AHPDD-М1.N, но при использовании формулы 1 или 2 он будет лишним т.к. данные жёстко детерминированы, а эксперты в принципе не нужны.
Для классического исполнения МАИ, всех остальных комбинаций нулевого поколения модификаций, а также для AHPMS-М1.N адекватность ОС под большим сомнением. При работе с матрицами, обладающими размером более чем 7±9, большими или даже суперформатами показатель ОС теряет всякий смысл.
Ограничение размера матрицы, заданное: Т. Саати – не более 7±9 (объясняет это психологическим порогом эксперта и ограниченностью верхнего предела целочисленной 9-балльной шкалы); табличные значения согласованности случайных матриц до 15. Если матрица размером более чем 7±9 и в ней нет равных объектов, при этом если использовать целочисленную 9-балльную шкалу, то показатель ОС никогда не будет меньше 0,1 – просто не хватит целочисленных интервалов измерения, их всего восемь.
Даже в пределах матрицы размером 15 если использовать дробночисленную шкалу это будет пределом для показателя ОС т.к. табличные данные случайной согласованности матрицы рассчитаны до 15, больших значений современная наука пока не даёт. Если матрица по размерам в диапазоне [7±9;…;15], то показатель ОС можно получить меньше 0,1 даже при наличии небольших и даже средних нарушений принципа транзитивности.
Также при правильной транзитивной логике и наличия в матрице оценок «0» показатель ОС чаще всего будет ОС < 0, а если нарушить принцип транзитивности, то показатель ОС не всегда адекватно сработает и покажет это нарушение ОС > 0,1. Это можно увидеть в классификаторах типа М1.2, М1.3, М1.4, М1.6, М1.7, М1.8 (таблицы 2 и 3) и др. возможных модификаций нулевого, первого и второго поколений.
Последняя ошибка измерений которую пропускает ОС > 0,1 – это эффект «Rank Reversal». По этому поводу автор приготовил отдельную публикацию.
По указанным и мн. др. причинам в том числе и описанных в ист. автора [11], показатель ОС является очень ограниченным в применении. Планируется специальная публикация с экспериментальными данными (которые у автора уже есть) по поводу адекватности показателя ОС.
В качестве альтернативы которая чаще всего может заменить чем дополнить показатель ОС для повышения качества измерений в МАИ предлагаются четыре варианта исполнения транзитивных цепей:
-
1. Транзитивная цепь из объектов Ai(j) на базе их измерений. Является базовым ориентиром для сравнения с транзитивной цепью варианта 4.
-
2. Расширенная транзитивная цепь из а ij ˅ аjj позволяет проверить транзитивность полученных оценок при помощи формулы 1 и 2. Если в транзитивной цепи обнаружатся ошибки, то следует проверить вычисления матричных оценок по формуле 1(2), т.к. корректное
-
3. Расширенная транзитивная цепь из 1/аij ˅ 1/аij . Обычно если транзитивная цепь варианта 2 не содержит нарушений, то транзитивная цепь данного варианта тоже не должна содержать нарушения. Справедливо и обратное утверждение.
-
4. Транзитивная цепь из локальных векторов приоритетов ԝ Ai является последним и важным вариантом. Эта цепь должна соответствовать базовому ориентиру, отображенному в варианте 1, а точность пропорций и/или измерений локальных векторов приоритетов будет зависеть от соблюдения принципа транзитивности в вариантах 2 и 3.
Примечание. Описанная альтернатива полностью правомерна и должна применяться для индивидуальных экспертных матричных оценок а ■J при использовании AHPMS(AM)-М1.N, FAHPMS-М1.N и для аij – AHPDD-М1.N. Что касается проверки согласованности ag агрегированных экспертных оценок а jj для AHPMS(AM)-М1.N и FAHPMS-М1.N, описанную альтернативу следует применять только совместно с математической статистикой (MS – Mathematical Statistics – математическая статистика). В ист. [11] автор уже описал основные положения MS для модификации МАИ. В классическом исполнении МАИ и его возможных модификаций AHP-М0.0(N), а также для AHPMS-М1.N применение указанной альтернативы бессмысленно, т.к. все, почти все или некоторые объекты не имеют привязки к единым или смежным измерителям и единым измерениям. Проверить согласованность n ag матричных оценок а ij и аjj можно при мощи MS в комбинации AHPMS-М1.N, но при этом следует знать, что эта проверка не будет иметь реального основания из за отсутствия указанной привязки к единым измерениям.
Именно по этим цепям есть возможность обнаружить нарушения принципа транзитивности на разных этапах вычислений локальных векторов приоритетов и при их обнаружении внести соответствующие исправления. Также при необходимости можно добавить побочные транзитивные цепи на базе ∑i=l аij или nij , или ∑i=l njj , или ∑j nij (пример для представленной экспериментальной базы FAHPMS-М1.N). По мнению автора, нет принципиальной важности в этих побочных цепях. Поэтому они и не показаны в экспериментальных данных.
Ещё один способ повышения эффективности использования резерва 3 будет описан в модификациях МАИ второго или др. возможных поколений. Суть идеи заключается в трансформации имеющихся данных измерений матричных объектов в девятеричное измерение. Это действие даст возможность сформировать идеальную матрицу вычислений матричных оценок, которые в свою очередь позволят использовать резервы роста точности измерений из показателя ОС, который в этой модификации должен быть равен нулю и приблизить пользователя МАИ к идеально точной оценке локальных векторов приоритетов. Пока выдвинутая идея является гипотезой.
Описанный резерв роста точности измерений 3 вполне применим для всех комбинаций М1.1–9 с учётом указанных требований. Данные эксперимента в таблице 2 полностью подтвердили правильность предложенной альтернативы из четырёх транзитивных цепей. Все транзитивные цепи друг друга подтвердили, поэтому ошибок в измерениях допущено не было.
Итак, после того, как изложены проблемы и их решения, связанные с поиском и использованием резервов роста точности измерений локальных векторов приоритетов в границах девяти модификаций МАИ первого поколения по результатам анализа экспериментальных данных в качестве эталона принимается комбинация М1.9. Именно этот эталон отличается от остальных восьми очень высоким уровнем точности оценки (измерения) векторов. Для того, чтобы измерить точность др. восьми комбинаций по отношению к 9-ой была использована операция модульной разности абсолютных значений локальных векторов приоритетов Δԝ Ai1 . :
Δԝ Ai1 .N = [ref. ԝ Ai1 .N -ԝAi1 .N ], (8) где ref. ԝ Ai1 .N – (reference – эталон) эталонный локальный вектор приоритета, измеряющий объект Аi в матрице парных сравнений, в экспериментальном примере – это комбинация 9– ref. ԝ Ai1 .9; ԝ Ai1 .N – не эталонный локальный вектор приоритета, измеряющий объект Аi в матрице парных сравнений, в экспериментальном примере для комбинаций М1.1–8.
Результаты вычислений представлены в таблице 3. Абсолютные отклонения локальных векторов 8-ми комбинаций по отношению к локальным векторам комбинации 9 составили в сумме 0,4836 для Аi-ых объектов с учётом горизонтального и для модификации М1.N с учётом вертикального принципа в равной конечной степени.
Далее для присвоения уровня точности измерений локальных векторов приоритетов, полученных при помощи комбинаций М1.1-8 воспользуемся формулами для вычисления среднеквадратических отклонений и коэффициентов вариаций по вертикальному, горизонталь- ному и вертикально-горизонтальному принципу:
=√
σMl.N
∑Ai М1.N —rpf w^l.9
∑ ( . )
N=const
П
∑Ai 1л Ml.N^2
∑ i=i |Δ wAi.| N=const
√
П
^M1 .N
aM1 .N
ref. .9
× 100,
^2
∑Ml.N М1.N_r„fwMl.9A
∑ ( . . . )
√
σ =
=√
,
N=1
П
N=1
П
,
∑М 1.N 1лU,M1.N^2
∑ . |ΔWAi . |
'A-
Al
wAi ref . .9
× 100,
∑Ai;N М1.N— refw^.1.9^
∑ ( М . . . )
σ M1 =√
N=1
П
=√
∑ ^;Г|ΔWAi'.N |^2
N=1
П
,
Ml _
.Ml
ref . .9
× 100,
Ml N MlN
где σ . и 4У . – среднеквадратическое отклонение и коэффициент вариации с учётом вертикального принципа для комбинаций М1.1-8 по отношению к эталону М1.9;
σ WA и – среднеквадратическое отклонение и коэффициент вариации с учётом горизонтального принципа для векторных оценок ԝ Ai комбинаций М1.1-8 по отношению к эталону М1.9;
Ml Ml
σ и 4У – среднеквадратическое отклонение и коэффициент вариации с учётом вертикально-горизонтального принципа для всех векторных оценок ԝ Ai , по всем комбинациям М1.1-8 по отношению к эталону М1.9;
ԝ М j1 . – абсолютное выражение локальных векторов Ai из числа не эталонных комбинаций М1.1-8;
ref. ԝ Ai1 .9 – абсолютное выражение локальных векторов Ai из принятой эталонной комбинации М1.9;
n – количество слагаемых действий в числителе формулы 9, 11 и 13.
Подставим данные из таблицы 3 в формулы 9-14 и выполним расчёты:
σ .
σ .
σ .
=√
=√
=√
, , ,
, , ,
= 0,0077,
σ
0,0094,
, , ,
, , ,
= 0,0107,
, , ,
, , ,
= 0,0094,
σ .
σ .
σ .
σ .
, , ,
, , ,
= 0,0221,
σ
σ
NPV.
()
σ
( , )
, , ,
, , ,
= 0,0075,
, , ,
, , ,
= 0,0098,
NPV
()
√
, , ,
, , ,
, ,
|
, , , |
||
|
() |
, , |
|
|
, , 8 |
= 0,0262 |
|
|
= , ×100= |
24,35%, |
|
|
vv 1(1) () |
, |
|
|
= , ×100= |
18,44%, |
|
|
vv 2(2) () , |
, |
|
|
, = ×100= |
8,59%, |
|
|
vv 3(3) () |
, |
|
|
|
, = ×100= |
8,59%, |
|
vv 4(4) () |
, |
|
|
|
, = ×100= |
4,64%, |
|
vv 5(5) NPV v v ^rv108 |
, |
|
|
|
, = ×100= |
5,28%, |
|
() in ry 173 |
, |
|
σ =
, , ,
, , ,
= 0,0110,
= 0,0206,
, , ,
, , ,
. =
|
. |
, , |
× |
100 |
= 4,62%, |
|
. |
, |
× |
100 |
= 6,45%, |
|
, |
||||
|
. |
, |
× |
100 |
= 5,64%, |
|
, |
||||
|
. |
, = |
×100 |
= 13,26% |
|
|
, |
||||
|
. |
, |
× |
100 |
= 4,50%, |
|
, |
||||
|
. |
, |
× |
100 |
= 5,89%, |
|
, |
||||
|
. |
, |
× |
100 |
= 6,57%, |
|
, |
||||
|
. |
, = |
×100 |
= 12,33% |
|
|
, |
||||
,
,
√
, , ,
, , ,
, ,

, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , , , ,
, , ,
= 0,0134,
^ м! = 0,0134 х 100 = 8,07%.
,
Расчёты дали следующие результаты: среднее вертикальное отклонение всех комби-
наций М1.1-8 от эталона М1.9 - 4Г м 1 = 7,41%;
= 0,0084,
√
, ,,
, ,,
,,
= 0,0067,
σ
()
σ
()
=√
=√
, ,,
, ,,
,,
= 0,0098,
, ,,
, ,,
,,
= 0,0098,
среднее горизонтальное отклонение всех векторных оценок из всех комбинаций М.1.1 -8 от эталона М1.9 - <7^7 = 11,65%; вертикальногоризонтальное отклонение всех векторных оценок из всех комбинаций М.1.1 -8 от эталона М1.9 - лг м 1 = 8,07%. Что частные, что усреднённые коэффициенты вариаций во всех случаях получились статистически значимыми отклонениями от эталона М1.9, особенно если цель эксперимента поиск решений проблем повышения точности измерений локальных векторов приоритетов. Поэтому все эти отклонения следует признать критичными, а на основании всех полученных экспериментальных данных и их анализа признать комбинацию М1.9 эталоном с очень высокой точностью измерений для первого поколения модификаций МАИ. Всем остальным комбинациям, согласно полученным данным вертикального анализа отклонений и всем др. результатам исследования
следует присвоить следующие уровни точно- числовой шкалы Е. Харрингтона, которые сти измерения локальных векторов с учётом представим в форме таблицы 4.
степени доверия к ним на базе вербально-
Таблица 4.
Присвоение уровней точности измерений локальных векторов и определения степени доверия к ним для девяти модификаций МАИ первого поколения на основании данных вертикального статистического анализа и других полученных результатов проведённого эксперимента*
Table 4.
Assigning levels of local vectors measurements accuracy and determining the degree of confidence in them for nine modifications of the first-generation AHP based on data from vertical statistical analysis and other results of the experiment
|
Уровень точности измерений локальных векторов по инверсированной вербальночисловой шкале Е. Харрингтона с учётом её адаптации к полученным среднеквадратическим отклонениям и вариациям | The level of accuracy of local vectors measurements on the E. Harrington inverted verbal-numerical scale, taking into account its adaptation to the obtained standard deviations and variations |
Классификаторы с учётом двух условий и значения их среднеквадратических отклонений и коэффициентов вариаций | Classifiers taking into account two conditions and the values of their standard deviations and coefficients of variations |
Степень доверия по вербальной шкале Е. Харрингтона к присвоенной точности измерений локальных векторов | The degree of confidence on the E. Harrington verbal scale to the assigned accuracy of measurements of local vectors |
|
Очень низкий уровень | Very low level 1 – 0,8 0,0221 – 0,0177 13,26 – 10,61% |
FAHPMS-M1.4 Ai(j) = Aj(i) > a jj = 0; Ai(j) = Aj(i) > a jj d = 1 0,0221 13,26% |
Очень низкая. Есть несимметричное искажение, т.к. ajjd = 1. Дополнительно для М1.4 есть неточность из-за применения целочисленной шкалы [1; ...; 9] |
|
FAHPMS-M1.8 Ai(j) = Aj(i) > a jj = 0; Ai(j) = Aj(i) > a jjd = 1 0,0206 12,33% |
||
|
Низкий уровень | Low level 0,7999 – 0,64 0,0176 – 0,0141 10,60 – 8,49% |
Не присвоен |
Не присвоена |
|
Средний уровень | Average level 0,6399 – 0,37 0,0140 – 0,0082 8,48 – 4,91% |
FAHPMS-M1.7 Ai(j) = Aj(i) > a jj = 1; Ai(j) = Aj(i) > a jjd = 0 0,0110 6,57% |
Средняя, т.к. принята не совсем точная дробночисленная шкала [1; .;9] |
|
FAHPMS-M1.2 Ai(j) = Aj(i) > ajj = 0; Ai(j) = Aj(i) > a jjd = 0 0,0107 6,45% |
Низкая, т.к. применяется целочисленная шкала [1; . ; 9] |
|
|
FAHPMS-M1.6 Ai(j) = Aj(i) > ajj = 0; Ai(j) = Aj(i) > a jjd = 0 0,0098 5,89% |
Средняя без особенностей |
|
|
FAHPMS-M1.3 Ai(j) = Aj(i) > a^ = 1; Ai(j) = Aj(i) > a jjd = 0 0,0094 5,64% |
Низкая из-за применения целочисленной шкалы [1; …;9] |
|
|
Высокий уровень | High level 0,3699 – 0,2 0,0081 – 0,0044 4,90 – 2,65% |
FAHPMS-M1.1 Ai(j) = Aj(i) > ajj = 1; Ai(j) = Aj(i) > a jj d = 1 0,0077 4,62% |
Низкая, т.к. применятся целочисленная шкала [1; .;9], а a jjd = 1 вносит дополнительное асимметричное искажение измерений. Высокий уровень полученный в первом столбце данной таблицы есть случайность |
|
FAHPMS-M1.5 Ai(j) = Aj(i) > a jj = 1; Ai(j) = Aj(i) > a jj d = 1 0,0075 4,5% |
Средняя с дополнительным асимметричным искажением измерений из-за a jjd = 1 |
|
|
Очень высокий уровень | Very high level 0,1999 – 0 0,0043 – 0 2,64% – 0 |
FAHPMS-M1.9 Ai(j) = Aj(i) > a ;' = 0 + 1 = 1 Ai(j) = Aj(i) > a Sd = 0 + 1 = 1 0 0% |
Очень высокая. Принятый эталон точности измерений локальных векторов приоритетов в модификации МАИ первого поколения |
*Во всех комбинациях, где ajj = 1 принято условно допустимое искажение измерений симметричного характера. | In all combinations where ajj = 1 a conditionally permissible distortion of measurements of a symmetrical nature is accepted.
При этом уровни точности измерений векторов по инверсированной вербальночисловой шкале Е. Харрингтона с учётом её адаптации к полученным среднеквадратическим отклонениям и коэффициентам вариации вычислялись по формулам:
LMA1 . =σ . . ×SS ., (15)
LMA2 . = . . ×SS ., (16) где LMA1 . и LMA2 .(the Level of Measurement Accuracy) – уровень точности измерений в модификациях МАИ первого поколения на базе показателей среднеквадратического отклонения и коэффициентов вариации;
MlN MlN
σ . . и . . – максимальная величина среднеквадратического отклонения и коэффициента вариации из всех девяти исследуемых модификаций;
ЅЅ . (Step of the Scale Harrington) – это шаг оригинальной вербально-числовой шкалы Е. Харрингтона, баллы.
Например, LMA1 , = 0,0221 × 0,8 = 0,0177 и LMA1 , = 13,26% × 0,8 = 10,61%.
Инверсия выражается в том, что самая высокая оценка по шкале Е. Харрингтона «1», её адаптированные аналоги 0,0221 и 13,26% характеризуют «очень низкий уровень», а «0» напротив «очень высокий уровень» точности измерений векторных величин в матрице МАИ.
Критерий степени доверия нужен для установления объективного статуса точности измерений комбинаций, т.к. на практике будут встречаться разные объекты, привязанные к измерителям и их измерениям, и разные размеры матриц. При этом значения коэффициентов вариаций будут существенно отличаться в пользу приближения или отстранения от принятого эталона измерения локальных векторов М1.9. Пользователям МАИ в первую очередь следует ориентироваться на вербальный показатель степени доверия к данным эксперимента, который объективно выставлен с учётом всех полученных результатов исследования, а уже во вторую очередь обращать внимание на среднеквадратические отклонения и коэффициенты вариаций, определивших LMA. Т.к. полученные статистические критерии не в полной мере учитывают искажения измерений векторов за счёт а =0 ∨ 1, целочисленных измерений, безразличия к тонким измерениям, др. неточности и ошибки измерений в разных комбинациях первого поколения о которых было уже много написано в данной статье и не только [11].
Такое не полное доверие к математическим критериям вызвано тем, что если изменить входные данные для эксперимента, то некоторые комбинации могут поменяться местами
Неизменно одно – это найденный эмпирическим путём через эксперимент эталон точности измерений векторных оценок в модификации МАИ первого поколения М1.9, которая исключает указанные и др. ошибки, неточности измерений. В статье уже более чем достаточно аргументов в пользу научной состоятельности этого утверждения.
Таким образом, можно сделать соответствующие выводы по результатам анализа реализованного эксперимента по поиску эталона измерений из девяти комбинаций первого поколения МАИ.
Заключение
Модификации М1.1–4 отклонены из-за низкой степени доверия к точности измерений локальных векторов приоритетов в матрице МАИ . Ранее [11] и в данной статье уже описывались неточности измерений, которые содержатся в М.1.1–1.4 – это: целочисленный характер измерений [1; …;9] только 8 основных интервалов измерения, где нет возможности тонких различий в измерениях и это приводит к ошибкам; все рассчитанные а ˅ а по формуле 1 измеряются от «1» и это тоже способствует появлению неточностей и ошибок в измерениях; влияние симметричных и ассиметричных помех (искажений) на точность и правильность измерений для М1.1, 1.3, 1.4.
Модификации М1.5-8 отклонены из-за не высокой степени доверия к точности измерений локальных векторов приоритетов в матрице МАИ . Дробночисленная шкала [1; …;9] отличается наличием в ней грубой ошибки измерений матричных оценок из-за необходимости соблюдать правило два: для дробночисленной шкалы [1; …;9] при обнаружении условия (а ˅ а )<1 округление делается всегда до единицы.
Неоднократно доказано, что по ряду причин, указанных в данной и др. ист. автора [11] показатель ОС является очень ограниченным в применении и не является гарантом точности и безошибочности измерений локальных векторов через измерения согласованности матричных оценок в поле матрицы. Показатель ОС адекватен только для индивидуальных
Шагеев Д.А. Вестник ВГУИТ, 2022, Т. 84, №. 1, С. 388-409 (не для агрегированных.) матричных оценок экспертов полученных при помощи комбинаций AHPMS(AM)-М1.N и FAHPMS-М1.N. ОС адекватен и в случае AHPDD-М1.N, но при использовании формулы 1 или 2 он будет лишним т.к. данные жёстко детерминированы, а эксперты в принципе не нужны.
Для классического исполнения МАИ, всех остальных комбинаций нулевого поколения модификаций, а также для AHPMS-М1.N адекватность ОС под большим сомнением.
Также при правильной транзитивной логике и наличия в матрице оценок «0» показатель ОС чаще всего будет ОС < 0, а если нарушить принцип транзитивности, то показатель ОС не всегда адекватно сработает и покажет это нарушение ОС > 0,1. Это можно увидеть в классификаторах типа М1.2, М1.3, М1.4, М1.6, М1.7, М1.8 (таблицы. 2 и 3) и др. возможных модификаций нулевого, первого и второго поколений.
Последняя ошибка измерений которую пропускает ОС < 0,1 – это эффект «Rank
Reversal».
В качестве альтернативы, которая чаще всего может заменить чем дополнить показатель ОС, принято четыре варианта исполнения транзитивных цепей для всех модификаций МАИ в первом, в том числе пригодных для нулевого и будущих поколений: из объектов A i(j); из аjj ˅ аij ; из 1/аij ˅ 1/аjj ; из локальных векторов приоритетов ԝ Ai . Все указанные альтернативы транзитивных цепей взаимно дополняют и позволяют перепроверять друг друга.
Что касается проверки согласованности ag агрегированных экспертных оценок аjj для AHPMS(AM)-М1.N и FAHPMS-М1.N, описанную альтернативу следует применять только совместно с математической статистикой [11]. В классическом исполнении МАИ и его возможных модификаций AHP-М0.0(N), а также для AHPMS-М1.N применение указанной альтернативы бессмысленно, т.к. все, почти все или некоторые объекты не имеют привязки к единым или смежным измерителям и единым измерениям. Проверить согласованность матричных оценок а ■j и а ij можно при мощи MS в комбинации AHPMS-М1.N, но при этом следует знать, что эта проверка не будет иметь реального основания из-за отсутствия указанной привязки к единым измерениям.
Также показатель ОС может применяться при выполнении определённых условий для разных модификаций и классификаторов первого поколения МАИ (см. табл. 4 из ист. [11]).
Для того чтобы исключить все указанные неточности и ошибки измерений по результатам проведённого эксперимента в качестве эталона следует принят классификатор М1.9. Отличительные особенности и преимущества для присвоения статуса «эталон измерения в первом поколении модификаций МАИ» следующие:
-
1. Принята шкала дробночисленная [0; …;8]+1 в 8 основных интервалах измерения на базе фундаментальной шкалы Т. Саати.
-
2. Исключены искажения в форме аjj =1 и а ij = 1, а приняты а■■ =0+1=1 и а = 0 + 1 = 1 для повышения точности и устранения ошибок разного рода в измерениях.
-
3. В формуле 2 добавлено арифметическое действие +1 для получения корректных матричных оценок 1/аij ˅ 1/а■■. При этом действие +1 применимо ко всем аij ˅ а ■j в границах матрицы, чтобы не допустить искажений и ошибок в измерениях.
-
4. В М1.9 произведено исключение комбинаций типа: а■■ =1 и а■■ = 1; а■■ =1 и а■■ = 0; а■■ =0 и а■■ = 1. Т.к. эти комбинации при реализации арифметического действия +1 внесут очень большие искажения измерений в исследовании.
-
5. Произведено дополнение и/или замена показателя ОС четырьмя вариантами построения транзитивных цепей из: Ai(j); аij ˅ а■j ; 1/аij ˅ 1/а ■j ; ԝ Ai . Эти варианты позволят выстраивать, проверять и перепроверять транзитивную логику и тем самым исключать возможные ошибки, которые могут быть допущены в процессе первичных, промежуточных и конечных вычислений (измерений) локальных векторов приоритетов в границах матрицы.
Все полученные результаты исследования полностью применимы для методики выбора эффективных проектов и др. областей науки в том числе и математике.
Направления дальнейшего развития: дополнительная проработка модификации МАИ искусственного свойства, где нет возможности привязать объекты матриц в иерархии к единым измерениям через единые или смежные измерители; повышение степени универсальности МАИ через расширение возможностей в процедуре конвертирования нечётких чисел разных форм в чёткие (пустые множества или детерминанты); дополнительная проработка новых научных категорий и расширение математической статистической критериальной базы с учётом адаптационных мероприятий, касательно модификаций МАИ первого поколения; описание решений проблем свёртки локальных векторов приоритетов и процедуры их иерархического синтеза для разных по структуре типов иерархий; описание решения проблемы «Rank Reversal»; дополнительное обоснование того, что показатель ОС является очень ограниченным в применении через экспериментальные данные; разработка решений в области АСУ и СППР в форме специальных программ, в основу которых заложены модификации нулевого, первого и последующих поколений МАИ для разных областей науки и методики выбора эффективных проектов в том числе; постановка научной проблемы и поиск её решения в направлении модификаций МАИ второго поколения; разработки единых требований по формированию рабочей группы экспертов для повышения качества и эффективности использования методики выбора эффективных проектов; разработки единого алгоритма реализации методики и стандартных организационных процедур; разработка и описание новой концепции и методологии по управлению развитием промышленного предприятия по показателям сбалансированности (гармонизации) денежных потоков; многие другие направления научного исследования.
Список литературы Поиск эталона измерений в модификациях МАИ первого поколения для методики выбора эффективных проектов и других областей науки
- Картвелишвили В.М., Лебедюк Э.А. Метод анализа иерархий: критерии и практика // Вестник Российского экономического университета им. Г.В. Плеханова. 2013. № 6 (60). С. 97-112.
- Коробов В.Б., Тутыгин А.Г. Проблемы использования метода анализа иерархий и пути их решения // Экономика и управление. 2016. № 8 (130). С. 60-65.
- Митихин В.Г. К вопросу решения многокритериальных задач на основе метода анализа иерархий // Cloud of Science. 2015. Т. 2. № 4. С. 519-529.
- Митихин В.Г. К вопросу анализа задач принятия решений с иерархической структурой // Международный научно-исследовательский журнал. 2015. № 8-2 (39). С. 110-114.
- Мощенко И.Н., Пирогов Е.В. К выбору оценочной шкалы в методе анализа иерархий // Инженерный вестник Дона. 2017. № 4 (47). С. 96.
- Ногин В.Д. Упрощенный вариант метода анализа иерархий на основе нелинейной свертки критериев // Журнал вычислительной математики и математической физики. 2004. Т. 44. № 7. С. 1261-1270.
- Подиновская О.В., Подиновский В.В. Анализ иерархических многокритериальных задач принятия решений методами теории важности критериев // Проблемы управления. 2014. № 6. С. 2-8.
- Саати Т.Л. Об измерении неосязаемого. подход к относительным измерениям на основе главного собственного вектора матрицы парных сравнений // Cloud of Science. 2015. Т. 2. № 1. С. 5-39.
- Власов Д.А. Методологические аспекты принятия решений // Молодой ученый. 2016. №. 4. С. 760-763.
- Титов В.А., Хайрулин И.Г. К вопросу о форме свертки локальных векторов приоритетов альтернатив по частным критериям в обобщенный вектор в методе анализа иерархий // Фундаментальные исследования. 2013. № 10-9. С. 2020-2025.
- Шагеев Д.А. Модификация МАИ для повышения точности измерений в методике выбора эффективных проектов и других областях науки // Вестник ЮУрГУ. Серия «Экономика и менеджмент». 2020. Т. 14. № 1. С. 93-115. doi: 10.14529/em200110
- Palma-Mendoza J.A. Analytical hierarchy process and SCOR model to support supply chain re-design // International journal of information management. 2014. V. 34. №. 5. P. 634-638. doi.org/10.1016/j.ijinfomgt.2014.06.002
- Benmouss K., Laaziri M., Khoulji S., Kerkeb M.L. et al. AHP-based Approach for Evaluating Ergonomic // Procedia Manufacturing. 2019. V. 32. P. 856-863. doi: 10.1016/j.promfg.2019.02.294
- Elliott M.A. Selecting numerical scales for pairwise comparisons // Reliability Engineering and System Safety. 2010. V. 95. № 7. P. 750-763. doi: 10.1016/j.ress.2010.02.013
- Franek J., Kresta A. Judgment Scales and Consistency Measure in AHP // Procedia Economics and Finance. 2014. V. 12. P. 164-173. doi: 10.1016/S2212-5671(14)00332-3.
- Gnanavelbabu A., Arunagiri P. Ranking of MUDA using AHP and Fuzzy AHP algorithm // Materials Today: Proceedings. 2018. V. 5. №. 5. P. 2. P. 13406-13412. doi: 10.1016/j.matpr.2018.02.334
- Bie P., Astrup A. Dietary protein and kidney function: when higher glomerular filtration rate is desirable // The American Journal of Clinical Nutrition. 2015. V. 102. №. 1. P. 3-4. doi: 10.3945/ajcn.115.112672
- Ishizaka A., Labib A. Review of the main developments in the analytic hierarchy process // Expert Systems with Applications. 2011. V. 38. №. 11. P. 14336-14345. doi: 10.1016/j.eswa.2011.04.143
- Meesariganda B.R., Ishizaka A. Mapping verbal AHP scale to numerical scale for cloud computing strategy selection // Applied Soft Computing. 2017. V. 53. P. 111-118. doi: 10.1016/j.asoc.2016.12.040
- Millet I., Saaty T.L. On the relativity of relative measures - accommodating both rank preservation and rank reversals in the AHP // European Journal of Operational Research. 2000. V. 121. №. 1. P. 205-212. doi: 10.1016/S0377-2217(99)00040-5
- Saaty T.L., Sagir M. An essay on rank preservation and reversal // Mathematical and Computer Modelling. 2009. V. 49. №. 5-6. P. 1230-1243. doi: 10.1016/j.mcm.2008.08.001
- Wang Y-M., Elhag T.M.S. An approach to avoiding rank reversal in AHP // Decision Support Systems. 2006. V. 42. №. 3. P. 1474-1480. doi: 10.1016/j.dss.2005.12.002


