Поиск объектов информационной системы с помощью решения задачи интервального поиска
Автор: Лялин Вадим Евгеньевич, Мальцев Сергей Андреевич, Тарануха Владимир Прокофьевич, Шишов Дмитрий Родионович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 1 т.11, 2013 года.
Бесплатный доступ
Статья посвящена оптимизации алгоритмов интервального поиска над различными базовыми множествами с использованием информационно-графовых моделей, направленной на сокращение временных затрат при восстановлении резервной информации.
Интервальный поиск, графовая модель, поиск информации
Короткий адрес: https://sciup.org/140191601
IDR: 140191601 | УДК: 519.71
Текст научной статьи Поиск объектов информационной системы с помощью решения задачи интервального поиска
Обозначим временной отрезок резервных копий множеством точек на отрезке [0; 1]. Задача интервального поиска является распространенной геометрической задачей, согласно которой при подаче запроса на поиск отрезка [а,6]с[0,1] необходимо перечислить элементы множества, входящие [ a ; b ]. В статье рассматриваются алгоритмы, возникающие при различных базовых множествах. В одномерной задаче интервального поиска множество записей ^nt есть отрезок [0,1], множество запросов
– множество всех отрезков [г/, v] с [0,1], или, другими словами, множество пар точек ( u , v ), таких, что 0 < и < v < 1, то есть
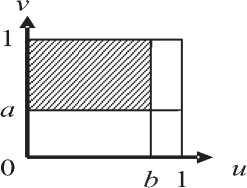
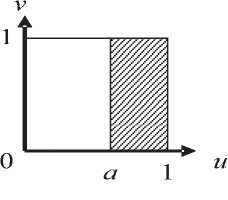
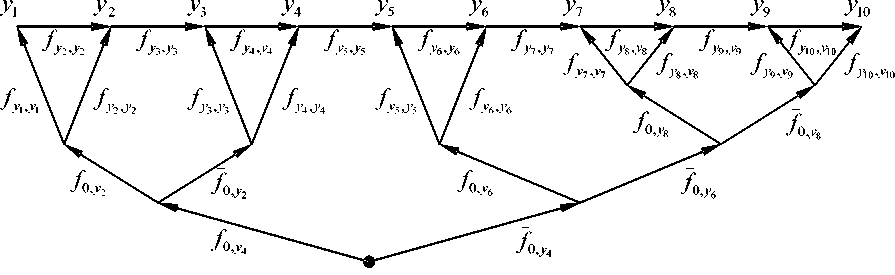
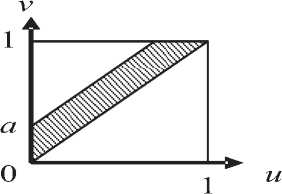
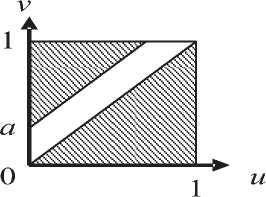
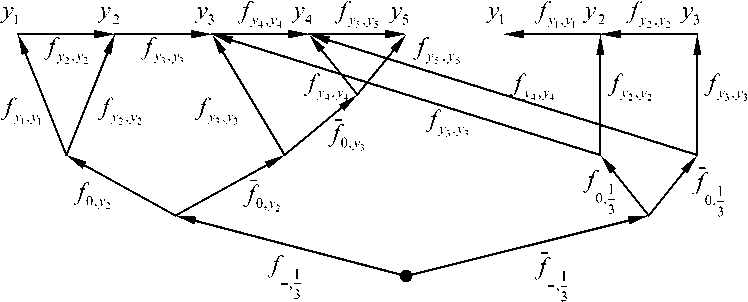
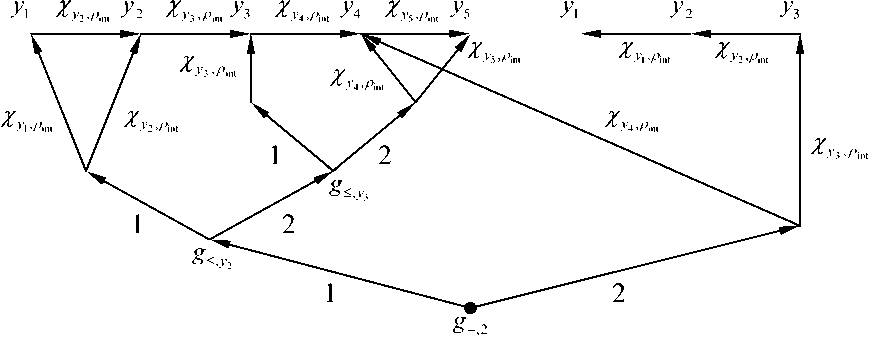
^int ={x = (w,v):0 Зададим на "^int вероятностное пространство (Л,.,^, где СУ – алгебра подмножеств множества ^int ’ состоящая из всех прямоугольников и прямоугольных равнобедренных треугольников со сторонами, параллельными осям координат, и на плоскости uOv [1]. P – вероятностная мера на СУ , определяемая плотностью распределения ве роятностей p(u,v) для любого В ЕСУ, то есть P(B) = ip(u,v) du dv. в Будем считать, что плотность вероятностей p(u,v) определена на всем квадрате [O,l]x[O,l], но p(u,v) = 0 при O^v)^^. Отношение интервального поиска Pint определим соотношением («’^Pint y^u Представление бинарного поиска с помощью графовой модели Базовое множество характеристических функций. Рассмотрим 1Цх,¥,рУ. \v\-k над базовым множеством Мрр0У ^ = {Zv.^, : V G y • Напомним, что z (X)= V’ecnuxP™t x [0, в противном случае. Отметим, что ^f имеет вид, представленный на рис. 1, а значит, Nf E СУ для любого предиката f eFv Кроме того, понятно, что Fx полно для ^int . Рассмотрим следующее утверждение. Если 1-^Х,У,р^и F^^F^ такие, что ^уе^Ху.реР’0^,?^^ J Nf)*0, ■f^F^Zy.p'f то TU,F) = \P\- Доказательство данной теоремы приводится в [1]. Рис.1. Характеристическое множество вида 1 Рис. 2.Характеристическое множество вида 2 Рис. 3. Характеристическое множество вида 3 Множество х = о<у,р^ч U ^) является множеством всех запросов х, таких, что Zy.pW – единственный предикат из F, принимающий на y значение «1». Покажем, что оно не пусто. Для этого необходимо найти хотя бы один запрос, который для произвольного y попадет в множество X. Рассмотрим запрос (у,у)- Для любого у G ^nt очевидно выполняется (У, У) е NZv^ , а для любого У'еУт1:у’*у выполняется (у, у) 4 Мх^ , то есть запрос (у, У) принадлежит множеству -^ 9 а значит, Х^0. Таким образом, T(I,F) = \v\ = k. Простое базовое множество. Обозначим Ма.ь = {-Y = Uhv)GХ;m :uay Рассмотрим случай, когда базовое множество предикатов равно F2 = {fayUaJ^Xm^ а базовое множество равно Е2ЦР2,0). Отметим, что Nf имеет вид, представленный на рис. 2, а значит, Nf G CT для любого предиката f g F^ и для любой записи у e Knt выполняется — / то есть F полно для . ЛУ.р„„ J v.y ’ *2 mt Тогда для сложности ЗИП i = Umt,v,Pm\при к = |K| —> oo справедливы следующие нижняя и верхняя оценки: . уеГ уеГ Доказательство данного утверждения приводится в [1]. Базовое множество логарифмического поиска. Рассмотрим базовое множество предикатов F3=F2u{/Oa:aG[O,l]},где если и < a если u> a Положим, что Рг=У3,0\ N1 имеет вид, представленный на рис. 3, а значит, Nfeg для любого / eF3. Пусть V – упорядоченная библиотека мощности k (F = b’l.--y^-. причем 0<у, <... n/,F3)<£p(O(y,,pint)) + 2]log24, где запись ]log2£[ обозначает наименьшее целое число, которое больше или равно log2 к . При этом ИГ, для которого получена данная оценка, строится нижеописанным способом. Возьмем произвольное ориентированное сбалансированное бинарное дерево с корнем и k листьями высоты ]log2 A:[, у которого все ребра ориентированы по направлению от корня к листьям. Обозначим правые и левые ребра бинарного дерева соответственно символами «П» и «Л». Сопоставим каждому листу слово, состоящее из символов «Л» и «П», согласно последовательности символов, приписанных ребрам, составляющим цепь из корня в рассматриваемый лист. Таким образом, исходящему из корня ребру будет соответствовать первый символ в записи, а входящему в лист – последний. Упорядочим листья согласно порядку слов, считая символ «Л» меньше символа «П». Обозначим i-ый лист ai и сопоставим ему запись yf ( i = l,k). Теперь определим нагрузку ребер дерева предикатами из F3. Для этого рассмотрим некоторую произвольную внутреннюю вершину P • Обозначим множество записей, соответствующих листьям ветвей, растущих из вершины , через Fp • Обозначим запись с минимальным в Fp номером как у,- , а с максимальным как yy . Заметим, что в ^у записи идут друг за другом, то есть v/g{/,7} y^Vp. Через P и (У обозначим вершины с ребрами, исходящими из P . Пусть y'. – запись с максимальным номером в Fp- • В случае, если P' – не лист, сопоставим ребру, ведущему из P в P' , предикат fo.v ■• а если лист, то – Uy'j.y’i . Правому ребру сопоставим fo 1< ’ если P" – не лист, и /y'.v" ’ если P" – лист, где y" – запись с максимальным номером в "^p" * Проделав данную операцию для всех внутренних вершин, мы определим нагрузку ребер. Теперь из всех листов otj (i = },k-}) выпустим ребра в листья ^/+1 и припишем этим ребрам предикаты *^>’/+1’>’i+l ' Полученный граф обозначим через u1 . На рис. 4 представлен пример графа u' при k = 10. Алгоритм поиска, соответствующий графу u' , состоит в следующем. С помощью бинарного поиска в отсортированной по возрастанию библиотеке за ]log2 A'[ шагов определяется самая левая запись, расположенная правее левого конца запроса либо совпадающая с ним. Далее, от найденной записи двигаясь вправо, просматриваемые записи поочередно сравниваются с правым концом запроса. При этом если оказывается, что просмотренная запись не больше правого конца, то она включается в ответ, иначе поиск завершается, т.е. этот алгоритм решения представляет собой традиционный поиск с помощью структуры, называемой прошитым двоичным деревом. Доказано [2], что описанный алгоритм оптимален по времени поиска в худшем случае и по памяти. Пусть, как и прежде, V – упорядоченная библиотека мощности k. Тогда для любого k существуют такие ЗИП Цх1йлр^ и плотность распределения вероятностей рЧиЛ, что для любого измеримого базового множества F3 справедлива следующая нижняя оценка сложности включающего поиска: T(FF3)>YP(O(y„pm^ + (3 log, к -1)^ 2/1 + 1 Рис. 4. Пример ИГ логарифмического поиска Оптимизация алгоритма бинарного поиска в информационно-графовой модели Базовое множество сверхлогарифмического поиска. Рассмотрим следующие два предиката: /_ „: Nu = {(?/, v) e Xint : 0 < v - и< a} 7-,,: N?_ = {(zz, v) g Xinl : (v - и > a) v (v - и < 0)}, где 0 < a < 1 . Характеристические множества Nf Л N-f представлены на рис. 5 и рис. 6 соответственно. Пусть базовое множество предикатов равно: F^=F^{f^, яе[0,1]}и{/_17, 67 g [0,1]}. Понятно, что N f G CT для любого M. Положим F.=kF4,0\ Пусть 1ЦХт,У,р^ – ЗИП типа ^inl . Построим ПИГ u2 над базовым множеством РаЦРл^, разрешающий данную ЗИП. Упорядочимзаписивбиблиотеке v = \У\,-;Ук} по возрастанию <У\^-.^укУ Обозначим m = [log2 /с], то есть максимальное целое число, не превосходящее log, к. Пусть 8 = Л-,Л. где у =^7, i = \,m. Для каждого s. (i = l,m) найдем целое число /, – номер ближайшей к si записи из V, меньшей чем s. , а в случае отсутствия такой записи примем I, = 0. Аналогичным образом, как и для базового множества логарифмического поиска, построим для V граф U1. Перестроим его в u по следую- щему алгоритму. Объявим корень u' как обычную внутреннюю вершину и обозначим как A . Проведем в A ребро с началом A , которое объявим корнем нового графа. Для этого ребра определим предикат /_,_!_ из F4 . Далее выпустим из корня еще одно ребро с предикатом и построим ориентированное сбалансированное бинарное дерево с m вершинами и корнем A , ребра которого направлены от A к концевым вершинам. Как и в случае логарифми- Рис. 5. Характеристическое множество вида 4 Рис. 6. Характеристическое множество вида 5 ческого поиска, введем понятия левого и правого ребер, что также порождает отношение порядка концевых вершин. В связи с этим пронумеруем концевые вершины по возрастанию и обозначим их через р\^рт . Таким образом, вершине Р'х будет соответствовать слово (Л, Л, …, Л), а вершине Р'т – (П, П, …, П). Нагрузка ребер предикатами определяется следующим образом. Возьмем произвольную внутреннюю вершину Р. Пусть PV – концевая вершина с наибольшим номером в ветви, исходящей из вершины с входящим левым ребром из Р . Исходящему из Р левому ребру сопоставим предикат fti s , а правому – /О 5 . Полная нагрузка ребер определяется после применения данной операции всех внутренних вершин дерева. В графе и' листья обозначены как , и им приписаны записи Ух^Ук соответствен-но.Построим еще k листьев (Zj,...,^ и припишем каждому а,' запись у, . Теперь для каждого iе{2, А} из листа a‘i проведем ребро в а'_х и припишем ребру (а', а'_х) предикат . Далее если /;. ^ 0, то для каждого i g {l,w} из Д' выпустим ребро в а' и припишем ему предикат fyi, УУ . При этом в случае / < к из Р'. построим еще одно ребро к листу а, и припишем ему предикат ^Уц+х ’Уц+х . После этого удалим все предикатные ребра, не являющиеся частью цепи из корня в каком-либо из листьев, вместе с их началами. Рис. 7. Пример ИГ сверхлогарифмического поиска Полученный граф обозначим через U . На рис. 7 представлен пример ИГ и для библиотеки V = {yt=^, к = \,5У Дадим неформальное описание алгоритма сверхлогарифмического поиска. Пусть нам дан запрос x = (u,v^XmX . Для начала вычислим длину интервала x. Если v-zz Таким образом, в первом случае помимо времени на перечисление ответа мы тратим время O(log2 A) , а во втором – O(log2 log2 A). Для данного ИГ была доказана верхняя оценка сложнос- ти [3]. Пусть плотность распределения вероятностей P T(I,F4)<^P(O(y,pmv)) + 2]log2 log21F|[ + 6 + 2c . yeV Мгновенное решение. Пусть G\ = ^,,„(Ma;) = max (1,]г/ •«?[)}, 1, если 0 2 в противном случае где Fx – базовое множество характеристических функций. Справедливо следующее утверждение [4]. Пусть ЗИП I = ^V,P^ – одномерная задача интервального поиска над базовым множеством F5, причем M=• Тогда если плотность распределения вероятностей Р<и,^, определяющая вероятность P на алгебре о, ограничена сверху некоторой константой с, то существует граф U Q объема ^(U) < 4k -1 + 6c[log, £], для которого ^P(O(y,pinl)) < T(I,F5) ^ I/Wy,pmV)) + 5 . Построим ИГ ^0 ’ на котором достигается данная оценка сложности. Возьмем точку Aи сделаем ее корнем графа. Выпустим из корня 2 ребра – левое и правое. Обозначим через P\ конец левого ребра, а через Pt – конец правого. Пусть m = 2c[log. A] . Зададим для корня переключатель g-^ip^ из G3 . Сопоставим левому и правому ребрам значения «1» и «2» соответственно. Из вершины P\ выпустим дерево бинарного поиска D для библиотеки V, как описано далее. Возьмем бинарное сбалансированное дерево с k листьями высоты ]log, k\_ с ребрами, направленными от корня к листьям. Если k нечетно, то в этом дереве существует внутренняя вершина, из которой исходит одно ребро, ведущее в лист, а другое – во внутреннюю. Из ребра, ведущего из данной вершины в лист, выпустим одно ребро, его конец объявим листом, а текущую вершину – внутренней. В полученном дереве сопоставим листьям слева направо в порядке возрастания элементов из V. Объявим все внутренние вершины дерева D с ребрами, ведущими к другим внутренним вер- шинам, вершинами переключения и припишем 1 левому исходящему из них ребру и 2 – правому, а самим вершинам припишем переключатель g<,XFv), где a – максимальная запись, достижимая из вершины, в которую ведет левое ребро из данной вершины. Все входящие в листья ребра дерева D объявим предикатными и каждому такому ребру, ведущему в лист с записью a, припишем предикат х«.Р1Лр\. Для дальнейшего удобства назовем множество переключательных ребер дерева D левой переключательной частью, а множество предикатных ребер – левой предикатной частью. Листья, которым соответствует запись V; , обозначим через at ^1 = \,к\ От каждого листа at (i = 1, к -1) выпустим ребро, ведущее в ai+\, и припишем ему предикат %Ут.РтEP. Множество этих ребер назовем правосторонней концевой цепью. Теперь из Pi выпустим m-\ ребер и пронумеру-емихчисламиот 1доm — 1, объявим Pt точкойпере-ключения с переключателем g,>p’^G\ • Обозначим P'l – конец ребра,исходящего из Pl и имеющего номер i.Введем множество номеров £ = {5,,...,^,.,} ,такое,что Si – номер записи из V такой,что ys – запись, ближайшая слева к точке -^ (i = 1,777 — 1 ), а если такой записи не существует,то . Возьмем k новых точек, объявим их листьями и обозначим a' (/ = 1,A). Каждому листу a' (i = \,k) припишем запись v.. Таким образом, каждая запись >’i приписана двум листьям – ai и a'. Из каждого листа a' (/ = 2, A) выпустим ребро, ведущее в лист a'-\ , и припишем ему предикат gFa. Это множество назовем левосторонней концевой цепью [1]. Теперь для каждой вершины Pi , если S, ^ o, то из Pi выпустим ребро, ведущее в a's и припи- Рис. 8. Пример ИГ U° шем ему предикат Ху^^р; если s, < к, то из P'i выпустим ребро, ведущее в ^ V +1 , и припишем ему предикат ^P. Правой предикатной частью назовем множество ребер, исходящих из вершин P', U = Vm-Y\ Граф, состоящий из корня Po ’ левой переключательной части, левой предикатной части, правосторонней концевой цепи, левосторонней концевой цепи и правой предикатной части, и будет искомым ИГ Uo . Заметим, что из полученного графа можно удалить все предикатные ребра, не являющиеся частью цепи из корня в один из листьев, вместе с вершинами, являющимися их началами, а также все переключательные вершины, из которых исходит одно ребро, вместе с данным ребром, заменив рассматриваемую переключательную вершину концом исходящего из него ребра. На рис. 8 представлен пример ИГ u° для библиотеки F = ^=^, k = Y5> и c = 0,5 . Заметим, что в этом случае m = 2, а значит, переключатель g.„, может принимать только значение «1». Таким образом, мы убираем из рассматриваемого графа этот переключатель вместе с исходящим из него ребром. Дадим неформальное описание алгоритма, приведенного выше. Пусть нам дано множество F = b\,-,ykV в котором мы должны произвести поиск. Упорядо-чимэто множество по возрастанию.Вслучае если оценка сверху c функции плотности распределения вероятностей появления запросов уже определена, то m возьмем как m = 2c[log2 A'] , если же константа c неизвестна, то в качестве нее можно взять любое число, например, c = 2 . Затем для V построим множество номеров S-^,,...,^.,}, описанное выше. Теперь поиск по произовльно взятому запросу производится следующим образом. Сначала определяется длина запроса x. Если x< -^, то во множестве V с помощью бинарного поиска находится запись, ближайшая к точке u справа. Далее от найденной записи просматрива- ются все записи из V слева направо и сравниваются с точкой v, пока очередная запись меньше v. Таким образом, производится ]log2 ^[ действий, не считая перечисления ответа. Если же v-z/>^, то, применяя функцию g-.m , : n ч получаем номер j точки m , входящей в интервал [m,v] . Далее просматриваем и сравниваем с u все записи из V справа налево начиная с записи с номером S j . Как только очередная запись окажется меньше u, с записи с номером S j + 1 просматриваются и сравниваются с правым концом запроса (точкой v) слева направо записи из V до тех пор, пока очередная запись не станет больше v. В данном случае, кроме перечисления ответа, мы производим 4 лишних действия (сравнение v — u с 77 ’ вычисление переключателя g- m , движение по правосторонней и левосторонней концевой цепи). Заметим, что параметр m определяется так, что средняя сложность первого случая не больше 1 при известной оценки сверху плотности распределения вероятностей запросов и не превышает некоторой константы, если эта оценка неизвестна.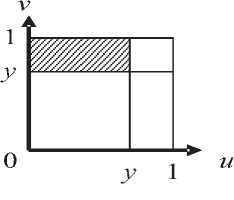
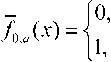
Список литературы Поиск объектов информационной системы с помощью решения задачи интервального поиска
- Гасанов Э.Э., Кудрявцев В.Б. Теория хранения и поиска информации. М.: Физматлит, 2002. -288 с.
- Тиори Т., Фрай Дж. Проектирование структур баз данных. М.: Мир, 1985. Кн. 1 -287 с.
- Тиори Т., Фрай Дж. Проектирование структур баз данных. М.: Мир, 1985. Кн. 2 -320 с.
- Гасанов Э.Э. О сложности поиска в базах данных//Искусственный интеллект. Межвузовский сборник трудов. Саратов: Изд. СУ, 1993. -С. 41-56.
- Гасанов Э.Э., Ерохин А. А. О быстром в среднем решении n-мерной задачи интервального поиска//Методы и системы технической диагностики. Тезисы X МК по проблемам теоретической кибернетики. Саратов: Изд. СУ, 1993. -С. 48-49.


