Поиск объектов на изображениях с использованием структурного дескриптора на основе графов

Поиск объектов на изображениях является актуальной задачей в различных областях компьютерного зрения: человеко-машинные интерфейсы, биометрия, дистанционное зондирование Земли, базы данных изображений, системы контроля технологических процессов и т.д.

Часто поиск объектов осуществляется на основе сопоставления с использованием дескрипторов. Дескриптор представляет собой метод, который идентифицирует некоторую область изображения на основе набора признаков. Выделяют следующие группы дескрипторов двумерных изображений [1, 2]: локальные двоичные дескрипторы, дескрипторы на основе спектрального представления, дескрипторы на основе базисных функций, дескрипторы формы. Следует отметить, что некоторые методы по своим характеристикам можно отнести к различным группам одновременно.

Локальные двоичные дескрипторы представляют собой описание небольшой области изображения в виде бинарных векторов. Наиболее известными локальными дескрипторами являются локальные двоичные шаблоны и их модификации (Local Binary Patterns – LBP) [3]. Также к этой группе относятся BRIEF (Binary Robust Independent Elementary Features) [4], ORB (Oriented BRIEF) [5], BRISK (Binary Robust Invariant Scalable Keypoints) [6] и т.д.

Дескрипторы на основе спектрального представления используют различные величины для идентификации областей: интенсивность, цвет, градиенты, статистические характеристики и т.д. По сравнению с двоичными дескрипторами, дескрипторы на основе спектрального представления требуют более интенсивных вычислений. К таким методам относятся следующие дескрипторы и их модификации: SIFT (Scale Invariant Feature Transform) [7], SURF (Speeded Up Robust Features) [8], DAISY [9], HoG (Histogram of Gradients) [10], корреляционные шаблоны (Sum of Absolute Differences (SAD), Sum of Squared Differences (SSD), Normalized Cross Correlation (NCC)) [11], Local Gradient Pattern (LGP) [12], код Фримана (Chain Code Histograms (CCH)) [13], признаки Хаара (HAAR Features) [14] и др.

Дескрипторы на основе базисных функций представляют описание изображения в заданных пространствах. Наиболее известным дескриптором на основе базисных функций является дескриптор Фурье [15]. К этой группе дескрипторов можно также отнести методы разреженного кодирования (Sparse Coding) [1]. Примером дескриптора из этой группы является метод «мешок слов» ( Bag of Words ) [16]. В дескрипторах на основе разреженного кодирования вместо базисных функций используется набор кодов для идентификации объектов.

Дескрипторы формы (Polygon Shape Descriptors) позволяют выполнять поиск объектов на основе та- ких характеристик, как площадь, параметры контура, моменты областей, центр тяжести полигона, коэффициенты прямоугольности и округлости, количество дыр и т.д. К наиболее известным подходам относятся MSER (Maximally Stable Extremal Regions) [17], код Фримана [13], дескриптор Фурье [15], контекст формы (Shape Context) [18], дескриптор на основе площади дискового покрытия [19], морфологические дескрипторы формы [20], дескриптор на основе ограничивающих областей [21], моменты региона [22], кривизна границ (curvature scale-space) [23], скелетон (Shock graphs) [24] и др.

Недостатком многих подходов является то, что в системах компьютерного зрения часто затруднительно выделить границы анализируемого объекта из-за эффектов резкой смены освещения, взаимных перекрытий, сложного текстурированного фона, изменения ракурса и т.д.

В работе предлагается структурный дескриптор, который идентифицирует область, состоящую из сотен и тысяч пикселей. Такая область сопоставима с изображениями объектов, поиск которых ведётся в системах компьютерного зрения. Для построения дескриптора предлагается использовать граф, вершинами которого являются особенности изображения. В предыдущих работах рассматривались вопросы нахождения соответствий [25], кластеризации особенностей [26, 27] и обнаружения объектов на основе спектральной теории графов [28]. В представленной работе новизной является следующее: рассматривается использование дескриптора для обнаружения лиц на изображениях, проводится исследование точности обнаружения лиц от угла поворота головы человека в пространстве.

1.    Разработка структурного дескриптора на основе графов

Преимуществом структурных подходов является то, что они позволяют анализировать большое множество элементов на основе малого количества простых составляющих и правил формирования графической модели. Также структурные методы позволяют описать те характеристики объекта, которые исключают его отнесение к другому классу, что повышает надёжность распознавания.

Предлагаемый структурный дескриптор включает в себя построение графов изображения-эталона и текущего изображения, вложение графов в векторное пространство и классификацию.

Построение графа на основе изображения

На вход дескриптора поступают текущее изображение и изображение-эталон, полученное на этапе инициализации. Следует отметить, что при поворотах объектов в пространстве некоторые особенности на различных снимках будут пропадать. Поэтому для повышения надежности поиска предлагается отслеживать центры масс сегментов особенностей. При повороте объекта набор особых точек в таких областях может измениться, но сама область будет присут- ствовать на изображении (рис. 1). Особенности выделяются с использованием детектора SURF [8].

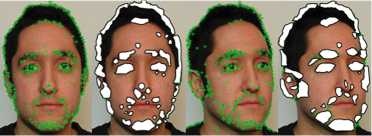
Рис. 1. Кластеризация особенностей, выделенных на изображении лица человека детектором SURF

Проводится кластеризация особых точек. В ходе данного процесса все особые точки, выделенные на изображении, группируются на основе метода связных компонент. В этом случае строится граф на основе триангуляции Делоне. Задаётся параметр W , и в графе удаляются все рёбра, длина которых больше W . Для подбора параметра W строится гистограмма распределений попарных расстояний между вершинами. Для изображений с хорошо выраженной кластерной структурой на гистограмме будет два пика, один из которых соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр W подбирается из зоны минимума между этими пиками. Соединёнными остаются только наиболее близкие вершины. Если в каком-либо полученном сегменте оказывается мало особенностей (меньше 3), то он не рассматривается далее. Таким образом, формируются сегменты, соответствующие наиболее характерным областям изображения.

После кластеризации осуществляется построение графа изображения. В качестве вершин выбираются центры масс полученных сегментов. Граф строится на основе триангуляции Делоне.

Нормализованная матрица Лапласа графа рассчитывается на основе выражения (1):

• 1, если u = v и d v ^ 0;

  L n = 1

  
  
  
  
  

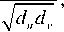
  если А ( u,v ) = 1;

  
  
  
  

• 0, в другом случае,

где d u , d v – степени вершин u и v соответственно.

Вложение графов в векторное пространство и классификация объектов на изображениях

Для поиска объектов предлагается выполнять вложение графов в векторное пространство. Это позволит представить изображения в виде векторов числовых характеристик, что даст возможность приближённого сравнения структур, не требующего точного сопоставления графов. Достоинством разрабатываемого подхода является инвариантность к повороту изображения на плоскости, так как спектральные характеристики графа не зависят от маркировки его вершин [29].

Для сравнения изображения-кандидата с эталоном предлагается использовать спектральную теорию графов. Для решения поставленной задачи выполняется вложение графов, построенных по сравниваемым изображениям, в векторное пространство [30]. В этом случае графы сравниваемых изображений преобразуются в вектор числовых характеристик, на основе которого выполняется сравнение.

На основе декомпозиции нормализованной матрицы Лапласа вычисляются спектральные характеристики графа:

L n = ФЛФ T ,

где Λ – диагональная матрица собственных значений λ₁, λ₂,…,λ |_V| ;

Φ – матрица собственных векторов φ ₁, φ ₂,…, φ |_V| .

Вложение графа основано на решении термодинамического уравнения:

d H d t

- L n H t ,

где t – время изменения состояния графа; H t – тепловое ядро.

Обычно значение времени подбирается опытным путём [30]. Однако кластеризация особых точек позволяет снизить зависимость результата от значения t . В рассматриваемых далее примерах начальное значение t = 0,01.

Тепловое ядро является решением уравнения (3) и вычисляется с помощью собственных значений и собственных векторов:

V

H t ( u,v ) = E e ^{- Xit} Ф i ( u ) ф / ( v ) ^{,                        (4)}

i =1

где λ i – собственные значения матрицы Лапласа;

φ i – собственные векторы матрицы Лапласа.

При проецировании графа в векторное пространство с помощью спектральных характеристик используются значения теплового ядра. Выполняется декомпозиция Юнга – Хаусхолдера:

H t = Y T Y ,

где Υ = ( y 1 … y u …y |V| ) – матрица координат размером | V |×| V |, в которой каждый столбец является вектором координат соответствующей вершины.

Раскрывая это выражение, получаем

Y = e ^{- (л} t ^/2) ф T

Следовательно, для вершины u координатный вектор рассчитывается следующим образом:

yu

^ X t                 x ₂ 1

e ² ф 1 ( и ) , e ² ф ₂ ( и )

—V ^T e 2 ф|V (u) J

При вложении графа в векторное пространство используется дифференциальная геометрия, в которой для описания связи между элементами матрицы координат используются составные кривые. По теореме Гаусса – Боне часть такой кривой может быть аппроксимирована дугой окружности. Такие кривые характеризуются параметрами кривизны, значения которой могут быть получены по значениям кратчайшего пути по окружности (длина дуги) и евклидовому расстоянию (длина хорды). Далее длину дуги будем обозначать d G , длину хорды – d E (рис. 2).

Квадратичное евклидово расстояние в этом случае имеет следующий вид:

^dE ( u, v ) ² = ( У и ^- y v ) T ( У и ^- y v ) =

V                         ₂                               (8)

= Ee"^ [фi( u)- Фi( v)] • i=1

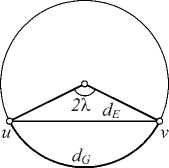
Рис. 2. Представление кривой с помощью дуги окружности

Составные кривые характеризуются параметрами кривизны. Для u и v значение кривизны рассчитывается следующим образом:

k ( u, v ) =     ¹ v                                 ⁽⁹⁾

R ( u, v )

где R ( u , v ) – радиус окружности.

Представим кривую дугой окружности с радиусом R ( u , v ). В таком случае длина дуги, то есть кратчайший путь по окружности между точками u и v , вычисляется следующим образом:

d_G = 2a R ( и, v ),

где a - угол дуги.

При вложении графов кратчайшее расстояние характеризуется весом ребра. Следовательно, для невзвешенного графа можно принять d G = 1. В таком случае угол a вычисляется следующим образом:

a = 1/2 R ( и , v ).                                   (11)

Евклидово расстояние равно длине хорды в рассматриваемой окружности между точками u и v :

d_E = 2 R ( и , v )sin ( a ) .                             (12)

В дальнейших расчётах необходимо избавиться от вычисления функции синуса неизвестного угла. Для этого предлагается разложить функцию sin( x ) в ряд Маклорена, то есть в ряд Тейлора при x =0:

I      a3a d„ = 2 R (и, v) a---1--

E              I

— ••• I .

Принимается, что в расчётах используется точность до двух членов последовательности ряда Маклорена. Таким образом, имеем следующее:

d = 1

^E      24 R ( u , v ) ²

Решая это уравнение в поисках R ( u , v ), получим следующее значение кривизны для точек u и v :

k ( и, v ) = 24 ( 1 - d_E ) .

Таким образом, каждый граф можно описать матрицей параметров кривизны. С помощью метрики Ха- усдорфа рассчитывается подобие между матрицами графов [30]. Имея матрицу подобия, с помощью метода многомерного шкалирования MDS (Multi Dimensional Scaling) можно определить, насколько соответствуют друг другу объект-кандидат и объект-эталон. Метод MDS используется для уменьшения размерности набора данных [31].

Пусть имеются два графа G 1 = ( V 1 , E 1 , k 1 ) и G 2 = ( V 2 , E 2 , k 2 ), где V 1 , V 2 – набор вершин; E 1 , E 2 – набор рёбер; k ₁, k ₂ – матрицы кривизны. Таким образом, расстояния между графами можно описать с помощью метрики Хаусдорфа:

HD ( G ,G 2 ) = max max min min I k ₂ ( I, J ) - k i ( i,j )| |. (16) ' ^e V j e V 1 I e V₂ J e V₂

С помощью метрики Хаусдорфа вычисляется матрица расстояний для графов объекта-кандидата и объекта-эталона. Для визуализации результатов используется метод MDS. Результатом применения метода MDS к матрице расстояний является представление, в котором характеристики графов описываются точками в евклидовом пространстве. Точки кластеризуются с помощью метода связных компонент для отнесения изображений объектов к какому-либо эталону.

Алгоритм реализации структурного дескриптора на основе графов

Алгоритм реализации структурного дескриптора на основе графов состоит из следующих шагов.

Шаг 1. Выделяются особенности изображения-кандидата и изображения-эталона.

Шаг 2. Проводится кластеризация особенностей двух изображений.

Шаг 3. На основе центров масс сегментов строятся графы Делоне. Рассчитываются нормализованные матрицы Лапласа (1) и тепловые ядра (4).

Шаг 4. С помощью преобразования Юнга – Хаусхолдера происходит проецирование координат вершин графов в векторное пространство (7).

Шаг 5. Рассчитываются значения кривых, связывающих точки. Строятся матрицы кривизны (15).

Шаг 6. Вычисляется матрица расстояний между характеристиками графа изображения-эталона и графа анализируемого изображения (16).

Шаг 7. Для визуализации данных применяется метод многомерного шкалирования, позволяющий отобразить степень близости изображения-кандидата к какому-либо объекту из базы эталонов.

Шаг 8. Происходит кластеризация точек в пространстве меньшей размерности на основе метода связных компонент. Вхождение точек в кластер свидетельствует об отнесении изображений объектов к определённому изображению-эталону.

2.    Исследование структурного дескриптора на основе графов

В ходе исследования были использованы следующие базы данных изображений: Carnegie Mellon University (CMU) Image Database, база данных Массачусетского технологического института MIT-CBCL

Face Recognition Database. На используемых изображениях меняется угол поворота объекта в пространстве. В данном случае обнаружение лица осуществляется на портретных снимках. При использовании разработанного дескриптора на изображениях реальных сцен происходит предварительное выделение особых точек, относящихся к области лица на изображении [26, 27].

Было проведено исследование разработанного подхода. Выполнялось сравнение с алгоритмом вложения графа, в основе которого лежит использование всех особых точек сцены [30].

На рис. 3 а вершинами графа являются все особые точки изображения, а на рис. 3 б вершинами графа являются только центры масс сегментов особенностей.

Рис. 3. Построение графа объекта по тестовым изображениям: а) вершинами графа являются все особенности изображения; б) вершинами графа являются центры масс сегментов особенностей

Были получены следующие результаты вложения графов с использованием метода многомерного шка- лирования (рис. 4).

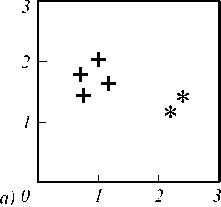
Рис. 4. Результаты вложения графов, изображенных на рис. 3, в векторное пространство: вершинами графа являются все особые точки изображения (а); вершинами графа являются центры масс сегментов особенностей (б)

Несмотря на то, что используются изображения одного объекта, в ситуациях, когда вершинами графа являются все особые точки изображения, алгоритм выделяет две разные группы. Напротив, разработанный алгоритм, рассматривая в качестве вершин графа центры масс сегментов особенностей, отнёс объекты к одной группе. На рис. 5 показано построение графов по изображениям лиц.

На рис. 6 показаны результаты вложения графов изображений лиц, представленные с помощью метода многомерного шкалирования. Разработанный дескриптор разделил на группы изображения лиц разных людей.

Одна из функций дескриптора – обнаружение головы человека на изображении. В данном случае сравнение работоспособности осуществлялось также с мето- дом Виолы – Джонса [32], так как он является некоторым стандартом в области компьютерного зрения и широко применяется в задачах поиска лиц на изображениях. Рассматривалась реализация метода Виолы – Джонса, когда при обучении лицо человека расположено строго анфас. Вычисление характеристик изображения на основе разработанного дескриптора вы- полнялось в аналогичных условиях.

а)

б)

Рис. 5. Построение графов по изображениям лиц:

вершинами графа являются все особенности изображения (а); вершинами графа являются центры масс сегментов особенностей (б)

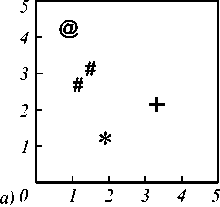
Рис. 6. Результаты вложения графов, изображенных на рис. 5, в векторное пространство: вершинами графа являются все особенности изображения (а); вершинами графа являются центры масс сегментов особенностей (б)

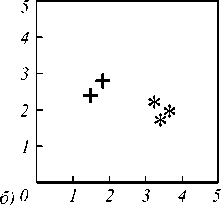
Было выполнено тестирование разработанного алгоритма на изображениях лиц из базы данных MIT-CBCL. В данном случае диапазон кивка, наклона и поворота головы составлял от 0 до 90°. При тестировании алгоритма для каждого лица из базы данных была составлена выборка изображений, на которых голова человека имела различную ориентацию в пространстве. Были получены следующие результаты (рис. 7). Главной особенностью разработанного подхода является то, что при любом значении угла поворота в плоскости XOY правильное обнаружение лица было не ниже 90%. Это связано с тем, что спектральные характеристики графа не зависят от маркировки его вершин.

При использовании метода Виолы – Джонса с увеличением углов поворота, кивка и наклона снижается точность правильного обнаружения лица человека. Напротив, разработанный алгоритм обладает большей точностью. В случаях вращения объекта в плоскости XOY точность обнаружения остается неизменной.

Заключение

При исследовании разработанного подхода выявлено, что дескриптор обладает инвариантностью к повороту изображения на плоскости, а также способностью обнаруживать объекты с углом поворота в про- странстве до 50°. Также выявлено, что использование центров масс сегментов особенностей в качестве вершин графа значительно повышает устойчивость подхода при изменении ракурса съёмки объекта.

Количество правильных обнаружений, %

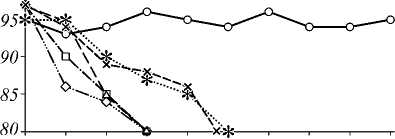
О 10 20 30 40 50 60 70 80 ОД

43--- Метод Виолы-Джонса в плоскости XOZ '   ’

-<-------Метод Виолы—Джонса в плоскости YOZ

-л--- Метод Виолы-Джонса в плоскости XOY

-х---- Разработанный дескриптор в плоскости XOZ

■■*......... Разработанный дескриптор в плоскости YOZ

-о Разработанный дескриптор в плоскости XOY

Рис. 7. Графики зависимости количества правильных обнаружений головы от угла поворота в плоскостях XOY, XOZ и YOZ для метода Виолы–Джонса и разработанного алгоритма

Работа выполнена при финансовой поддержке государственного задания Минобрнауки России (проект № 2.1950.2017/ПЧ), РФФИ (проект № 16-37-00235).