Поиск однотипных графиков нагрузки энергообъекта

В рамках текущего оперативного управления режимом работы Единой энергосистемы в диспетчерских центрах Системного оператора имеются большие ретроспективные массивы данных с получасовой дискретностью по всем крупным подстанциям и потребителям, а также есть массивы данных с секундной дискретностью за последние несколько недель. Эти секундные данные потенциально содержат в себе информацию о регулирующем эффекте нагрузки.

Существуют два основных подхода к оценке регулирующего эффекта нагрузки: измерительный, на основе данных измерений, и компонентный, на основе данных численного моделирования [1–9].

Измерительный подход для идентификации математической модели нагрузки, а также регулирующего эффекта, предполагает определение параметров и вида модели на основе обработки непосредственно измеренных значений мощности нагрузки. При этом возможно проведение как активного эксперимента (с принудительным изменением уровня питающего напряжения), так и пассивного эксперимента (наблюдение за текущими параметрами режима).

В основе компонентного подхода лежит численное моделирование режимов работы комплексного узла нагрузки, с учётом представления небольших нагрузок их реальными математическими моделями. Пассивный измерительный подход позволяет избежать дорогостоящих системных испытаний, а также трудоёмкого моделирования узлов нагрузки. Однако точность такого подхода во многом зависит от временной дискретности и погрешности измерительных комплексов. Важно отметить две основные проблемы при обработке данных пассивных измерений: во-первых, это небольшая амплитуда колебаний питающего напряжения, а во-вторых, постоянное изменение состава и режима работы единичных электроприёмников. Последнее также характерно и в случае проведения активных экспериментов в энергосистеме.

Для извлечения из массивов данных измерений информации о виде и параметрах математической модели нагрузки необходимо выявить статистически равновесные состояния исследуемого объекта [10]. Этапы поиска статистически равновесных состояний нагрузки можно разделить на три этапа, как показано в таблице. В настоящей статье далее рассматривается алгоритм поиска однотипных суточных графиков нагрузки.

Обработка экспериментальных данных для однотипных графиков нагрузки может позволить решить проблему поиска интервалов времени, когда включенный состав и режимы работы единичных электроприёмников близки. Это позволяет увеличивать выборку данных измерений за счёт объединения информации для однотипных суточных графиков нагрузки. В результате появляется возможность создания алгоритмов автоматизированной оценки параметров математической модели нагрузки и величины регулирующего эффекта.

Этапы поиска статистически равновесных состояний нагрузки

Первый этап	Второй этап			Третий этап
Узел нагрузки	Сезон	День недели	Час или полчаса	Статистически равновесные состояния
Нагрузка 1; Нагрузка 2; …;	Весна; Лето; Осень; Зима	Понедельник; Вторник; Среда; …; Воскресенье	Интервал 1; Интервал 2; …; Интервал M	Состояние 1; Состояние 2; …; Состояние Y

Актуальность и научная значимость вопроса

Выявление однотипных графиков нагрузки позволяет сформировать подход к решению нескольких задач, например: формирование статистической выборки данных измерений комплексной нагрузки для одного и того же включённого состава единичных электроприёмников или подбор оптимального тарифного плана покупки электроэнергии у электроснабжающей компании. Разработка соответствующих методов идентификации статистических характеристик нагрузки по данным телеизмерений обеспечивает возможность не только идентификации математической модели нагрузки, но и прогнозирования вида и параметров модели в будущем.

Типы подобия временных рядов

В качестве исходных данных для поиска «похожих» суточных графиков нагрузки приняты временные ряды усредненных на небольших интервалах времени внутри суток значений активной и реактивной мощности.

В зависимости от целей поиска однотипных графиков нагрузки, возможно выделить несколько типов подобия временных рядов похожих:

• 1)    во времени;

• 2)    по форме;

• 3)    по структуре.

В первом случае ведется поиск временных рядов, в которых особые точки, а также интервалы убывания и возрастания, близки или точно соответствуют друг другу. Тогда близкие временные ряды будут отражать не только характерные особенности суточного цикла потребления, но и содержать в себе информацию о включенном составе электроприёмников и их загрузке в технологическом цикле, а также действиях регулирующей автоматики и персонала по изменению параметров электрического режима. Именно такой тип подобия будет рассмотрен далее.

Во втором случае интерес для анализа представляет именно поиск однотипных форм графиков нагрузки. Основное отличие от предыдущего случая заключается в необходимости нормирования суточных данных измерений, что позволяет отстроиться от конкретных численных значений. Этот тип подобия будет характерен для решения задач прогнозирования электропотребления и выявления типовых графиков электропотребления.

В третьем случае выполняется поиск последовательностей с одинаковыми законами изменения, как глобальными (периодичность повторения), так и локальными. Этот случай будет характерен для задач анализа изменчивости суточных графиков нагрузки в разрезе нескольких лет.

Представление данных

Один из лучших способов кластеризации временных рядов – это кластеризация их не как временных рядов, а без учёта временной взаимосвязи между измерениями. Специфика рассматриваемой задачи и набор исходных данных в целом позволяют применить такой способ.

Пусть

P j = ^{Р 1 , Р 2 ,-,Р т ^} и Q j = {4 1 ,4 2 ,-, 4 т }, j E N - суточные временные ряды активной и реактивной мощности, содержащие Т отсчётов по времени; N - количество суточных графиков нагрузки для кластеризации. Значения временных рядов в каждый момент времени есть одномерные вещественные переменные р , и 4 , , i E Т. Для удобства описания и выполнения расчетов можно объединить суточные временные ряды активной и реактивной мощности:

D j =P j ^uQ j = ^{Р 1 ,Р 2 ,-,Р т ,4 1 ,4 2 ,-,4 т ^}.

Тогда F(D j ,D_k), при j * к и k,j E N есть некоторая функция, измеряющая насколько D j отличается от D_k . В общем случае эта функция может не отвечать математическому определению метрики, например, при использовании алгоритма минимальной прыжковой стоимости [10].

Алгоритм оценки подобиясуточных графиков

Представим каждый временной ряд как некоторую точку в 2 N -мерном пространстве, тогда в качестве алгоритма оценки подобия рядов D j можно принять один из стандартных алгоритмов кластеризации данных, например, k-means [11, 12]. Алгоритм основан на минимизации суммарного расстояния V от точек кластеров до центра кластера:

V = M^Ws^ ^ min, где С - число кластеров; Кс1 - число точек отнесенных к кластеру с номером cl; DScl - центр кластера cl, соответствует среднему графику нагрузки для данного кластера.

В качестве функции F(D j ,D_k) оценки отличия между суточными графиками нагрузки использ уется Евклидово расстояние:

F(D j ,D_k) = JlKP ij -Pi^+ZKq ij -qi^² .

Одним из основных недостатков данного а лгоритма является необходимость предварительной оценки числа кластеров и выбора начальных ра змещений кластеров.

Для решения первой проблемы выполнена с е рия расчётов с различным числом кластеров, и к дальнейшему рассмотрению принят тот случай, для которого изменение суммарно го расстояния L от точек до центров своих кластеров ниже некот орого порогового значения ^L:

^-^- < AL[%], ls-i где Ls - суммарное расстояние от точки до центра своего кластера при числе кластеров s Е С; ^L [%] -пороговое значение изменения суммарного рас- стояния при увеличении числа кластеров (принято значение ^L, равное 5 %).

Алгоритм выбора начальных приближений может быть основан на следующих идеях: выбор случайных точек данных в качестве начальных приближений или использование некоторого алгоритма выбора начальных приближений, например, k-means ++ [13]. Далее рассмотрены оба случая.

Практическая апробация алгоритма

В качестве объекта исследования для поиска типовых суточных графиков электропотребления принята подстанция 110 кВ, питающая промышленную нагрузку (сборочный конвейер в машиностроительной отрасли) с небольшой долей кому-нально-бытовой и офисной нагрузки. Суточные графики средней мощности на получасовом интервале представлены на рис. 1 и 2. На рисунках «бледными» линиями показаны суточные графики нагрузки, а ярким цветом – усредненный суточный график нагрузки для каждого месяца. На рис. 2 видна особенность данного комплексного узла нагрузки, которая заключается в том, что для одного и того же дня недели существует несколько характерных графиков электропотребления. В пер-

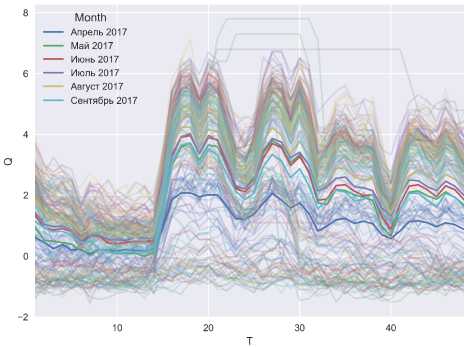
Рис. 1. Данные измерений за 6 месяцев

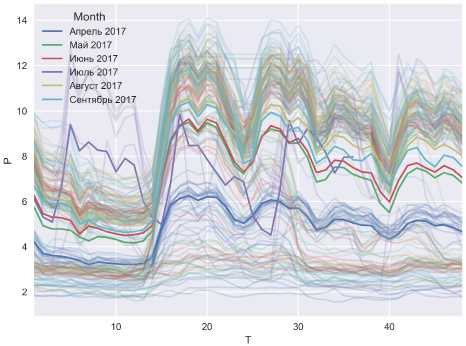
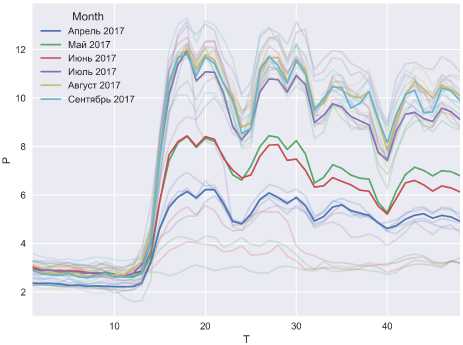
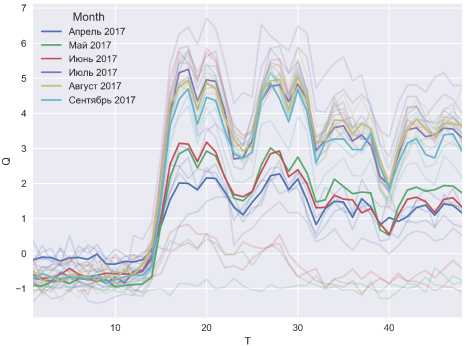
Рис. 2. Данные измерений за 6 месяцев, по понедельникам

вую очередь именно этот факт обуславливает н е обходимость автоматической группировки граф иков электропотребления по типам.

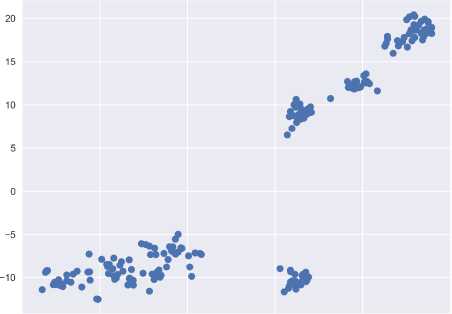
Для визуализации полученного множества т очек D j в пространстве размерностью 2N в двух измерениях можно воспользоваться алгоритмом t-SNE ( t- distributed Stohastic Neighbor Embedding ), предложенным Д. Хинтоном в работе [14]. Ос нов ная идея алгоритма заключается в поиске такого отображения многомерного пространства в дву х мерное, чтобы расположенные далеко друг от др у га точки были на плоскости удалёнными, а близко расположенные также отобразились бы как бли зкие. Результаты расчётов представлены на рис. 3.

На рис. 3, б видно, что при уменьшении кол и чества суточных графиков нагрузки «исчезает» их явная группировка. Это обусловлено особенн о стью обработки данных алгоритмом t-SNE . Увели чение объема выборки позволяет нивелировать эту проблему.

Предварительно требуется определить сл едующие расчётные условия:

• 1.    Необходимое число запусков алгоритма с

• 2.    Оптимальное количество кластеров в выборке, в соответствии с приятым значением Д.

одним и тем количеством кластеров и алгоритмом выбора начальных приближений, чтобы достичь наилучшего разбиения выборки на кластеры.

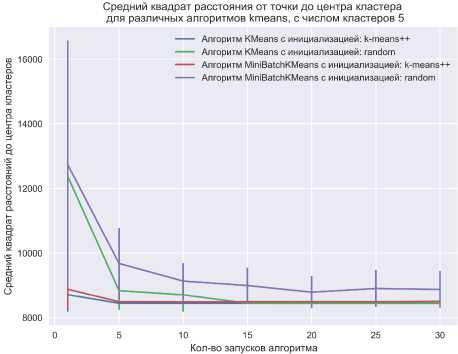
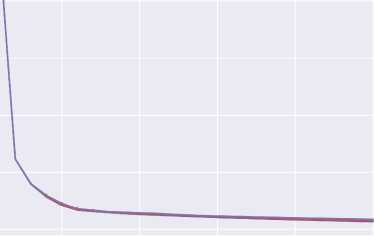
Поиск оптимальных расчётных условий выполнялся для комбинации следующих алгоритмов кластеризации: классический k-means и алгоритм minibatch k-means . Особенностью алгоритма minibatch k-means является то, что исходный набор данных на каждом расчётном шаге представлен меньшим случайно выбранным подмножеством данных. В качестве алгоритмов выбора начальных приближений размещения кластеров рассмотрены следующие два: случайное размещение кластеров и алгоритм k-means ++. Результаты расчётов представлены на рис. 4. На рис. 4, а вертикальная линия на графике описывает стандартное отклонение суммарного квадрата расстояний от точки до центра своего кластера по результатам серии расчётов. График описывает средний суммарный квадрат расстояний. Для дальнейшего расчёта выбраны следующие расчетные условия: 6 кластеров;

-10                -5                 0                  5                 10

а)

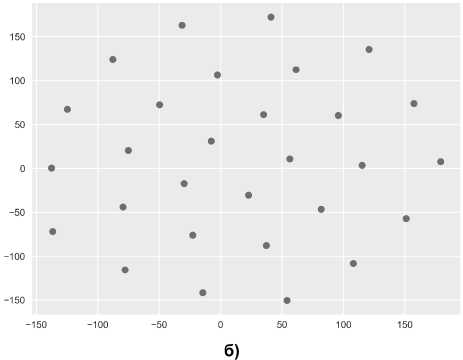
Рис. 3. Представление точек на основе алгоритма t-SNE , соответствующих графикам нагрузки: а – полная выборка; б – за один месяц

а)

Рис. 4. Суммарный квадрат расстояний от точек до центров кластеров при различных условиях расчётов

Средний квадрат расстояния от точки до центра кластера для различных алгоритмов kmeans, с числом запусков 10

---- Алгоритм KMeans с инициализацией: k-means++

---- Алгоритм KMeans с инициализацией: random

---- Алгоритм MiniBatchKMeans с инициализацией: k-means++

---- Алгоритм MiniBatchKMeans с инициализацией: random

5               10               15               20               25

Кол-во кластеров

б)

20 запусков алгоритма кластеризации; алгоритм k-means , так как кластеризация по полной выбо рке занимает приемлемое к оличество времени (н есколько секунд).

Результаты расчётов представлены на рис. 5–7.

Видно, что результаты апробации алгоритма подтверждают возможность осуществления группировки суточных графиков нагрузки.

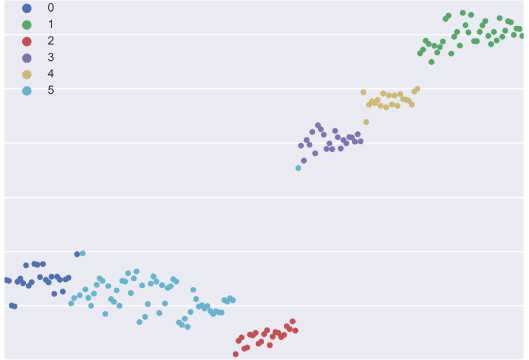
Рис. 5. t-SNE представление результатов кластеризации графиков нагрузки

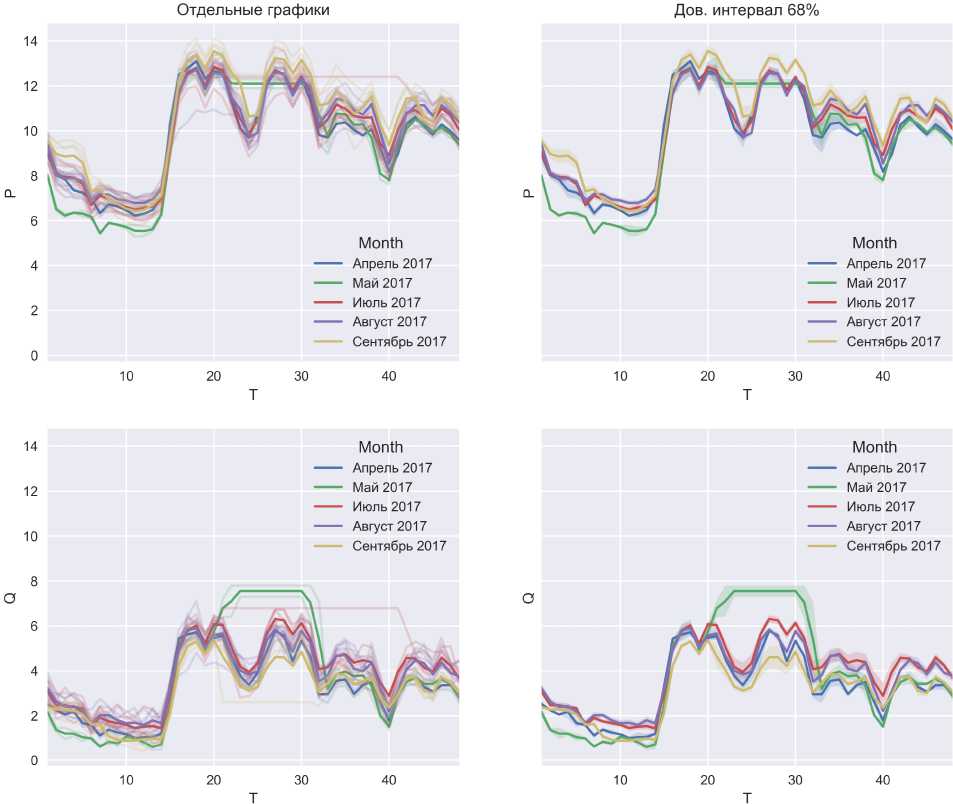
Рис. 6. Первая найденная группа графиков нагрузки с разбивкой по месяцам

Month

--- Апрель 2017

- Май 2017

--- Июнь 2017

--- Июль 2017

Август 2017

Сентябрь 2017

Дов. интервал 68%

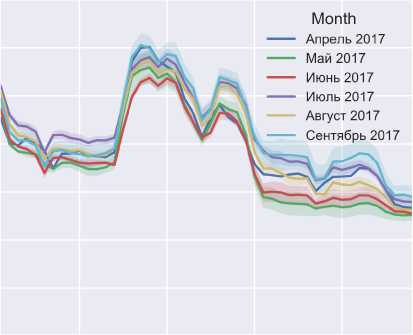
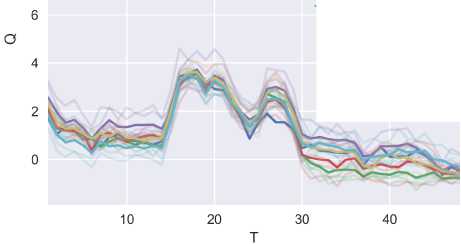
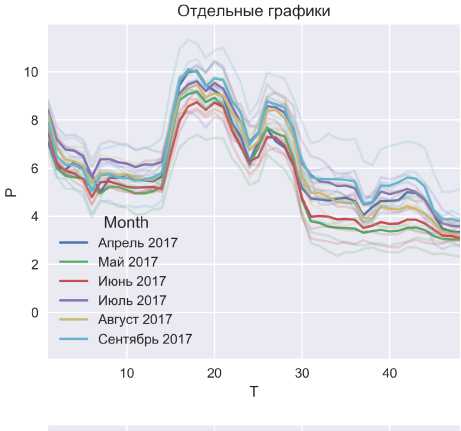
Рис. 7. Вторая найденная группа графиков нагрузки с разбивкой по месяцам

Заключение

В статье представлен алгоритм выявления о днотипных графиков нагрузки с использованием статистических алгоритмов анализа данных. Эту идею можно использовать для автоматизирова н ной оценки типовых графиков нагрузки по данным массивов телеизмерений. Данный подход позвол я ет оценить интервалы времени с близким в клю ченным составом единичных электроприёмников и их уровнем загрузки в технологическом проце с се в составе комплексного узла нагрузки.

В том случае, если важно оценить только форму графика нагрузки, без учёта конкретных значений активной и реактивной мощнос ти, ус реднённые значения суточного электропотребл е ния можно представить в относительных един и цах, где за коэффициент нормировки принято ма к симальное значение мощности в сутках.

Дальнейшее направление развития данной идеи классификации графиков нагрузки нац елено на настройку и апробацию алгоритма EM-алгорит ма разделения смеси распределений (в частности смеси гауссовых распределений).