Поиск рациональной геометрической схемы пространственной металлической конструкции покрытия большепролетного спортивного сооружения

Строительство уникальных зданий и сооружений journal homepage: of Unique Buildings and Structures .,.„,.

В последнее время в России в связи с проведением целого ряда международных соревнований, таких как Универсиада в Казани в 2013 г., Зимние Олимпийские игры в Сочи в 2014 г., Чемпионат мира по футболу в 2018 г. и др. особое внимание уделяется вопросу проектирования и строительства уникальных большепролетных спортивных сооружений. Каждая вновь построенная спортивная арена демонстрирует последние достижения архитектуры, науки и техники, знания и творческий потенциал проектировщиков.

При создании нового уникального сооружения основным принципом формообразования в большинстве случаев является архитектурная идея (приемы фрактальной архитектуры и мимесиса) [41]. Подобные сооружения требуют комплексного подхода при проектировании целого ряда специалистов: архитекторов, конструкторов, технологов. На всех этапах проектирования объекты претерпевают множество изменений в архитектурном и конструктивном плане и, как следствие, требуют постоянного перерасчета. Кроме того, в связи с ужесточившимися в последние десятилетия требованиями к экономичности сооружений, перед проектировщиками встает задача выбора оптимального решения, т.е. появляется необходимость осуществлять вариантное проектирование. Использование вычислительных комплексов, основанных на численных методах расчета конструкций, сокращает трудоемкость проектных работ и ускоряет сроки проектирования.

Одним из основных численных методов для расчета строительных конструкций является метод конечных элементов (МКЭ). Метод имеет обоснованную теоретическую базу, легко программируется. Возможности реализации его в САПР изложены в трудах Городецкого А.С. [6,7], Перельмутера А.В., Сливкера В.И. [9]. На сегодняшний день на основе МКЭ создано множество вычислительных комплексов, из которых одним из наиболее востребованных в России и странах СНГ является "Интегрированная система прочностного анализа и проектирования конструкций Structure CAD Office" (SCAD) [5].

Обзор литературы

Создание новых конструктивных схем покрытий большепролетных уникальных спортивных сооружений невозможно без использования мирового и отечественного опыта проектирования и строительства подобных объектов.

На сегодняшний день существует множество работ по исследованию подобных сооружений в России и странах СНГ [10-20]. Изучен также иностранный опыт по проектированию и анализу работы пространственных покрытий различных сооружений [25-38]. Наибольший интерес представляют работы по исследованию покрытий таких объектов, как Большая спортивная арена в Лужниках [10-12], Ледовый дворец спорта на Ходынском поле в г. Москва [13], Большая ледовая арена для хоккея с шайбой в г. Сочи [18], а также зарубежных объектов: футбольный стадион в Браге [25, 26], Олимпийский стадион в Монреале [27], стадионы в Шанхае [28], Пирее [38] и Риме [33].

Несмотря на большое количество работ и публикаций по данной тематике, большая часть работ посвящена проблемам проектирования, исследованиям их работы и мониторингу в условиях их дальнейшей эксплуатации и не затрагивает вопросы анализа конструкций на основе численных методов. Многие авторы ставят своей целью, как правило, создание расчетной модели сооружения и ограничиваются лишь анализом напряженно-деформированного состояния элементов покрытия.

Наиболее близки к рассматриваемой тематике работы Назарова Ю. П. [18, 19], расчет покрытия АВК «Внуково-1» [20], а также исследования покрытий стадионов в Браге [25-26] и Монреале [27]. Некоторые частные случаи оптимизации строительных конструкций освещены в работах зарубежных авторов [39-40]. Однако, найти конкретные работы по созданию четких алгоритмов оценки рациональности конструктивных решений покрытий подобного рода сооружений применительно к конкретным вычислительным комплексам не удалось.

Постановка задачи

Цель данной работы — исследовать напряженно-деформированное состояние несущих конструкций большепролетного сооружения на моделях расчетных схем, созданных в среде SCAD, исследовать материалоемкость полученных вариантов с целью определения рациональных решений.

Из поставленной цели вытекают следующие задачи:

• -    создать КЭ модели пространственной металлической конструкции покрытия стадиона Фишт в SCAD;

• -    провести анализ напряженно-деформированного состояния элементов основной несущей конструкции покрытия;

• -    обосновать критерий оптимизации (целевую функцию);

• -    осуществить сравнение исследуемых вариантов модели для выявления рациональных конструктивных решений по критерию металлоемкости.

Краткая характеристика объекта

В конструктивном отношении Центральный стадион (стадион Фишт) состоит из 6-ти этажного здания с трибунами и подтрибунными помещениями, запроектированными в монолитном железобетонном каркасе, и металлического большепролетного покрытия над трибунами.

Покрытие над трибунами стадиона (рисунок 1) представляет собой неправильную криволинейную поверхность, образованную конструкциями арочных плоских ферм переменного пролета с треугольной решеткой. Большепролетное покрытие имеет две секции над восточной и западной трибунами.

Рисунок 1. Архитектурный облик центрального олимпийского стадиона

Секции по фронтальному краю покрытия поддерживаются конструкциями основных (главных) арок А1 и А2. Пролет арок – 285 м, а высота – 70 м. Каждая из двух 4-х поясных арок имеет форму трапеции в поперечном направлении и отклонена от вертикальной оси на 14º в сторону трибун. Сечение основной арки запроектировано переменной высоты 7.0÷14.4 м и ширины 5.5 м. С южной стороны сооружения основная арка жестко защемлена в устои фундамента за счет опирания 4-х поясов и системы раскосов арки на траверсные опоры. С северной стороны сооружения основная арка опирается нижними поясами и системой раскосов на цилиндрический шарнир [4]. Шарнирно неподвижная цилиндрическая опорная часть (одна степень свободы) обеспечивает поворот опорных узлов главной арки в своей плоскости с коэффициентом трения не более 3% при расчетной температуре наружного воздуха наиболее холодной пятидневки.

Поперечная устойчивость основных арок обеспечивается рядом второстепенных, параллельно расположенных, полуарок Р1…Р10, отходящих в перпендикулярном направлении от основных арок. Шаг полуарок 28 м, пролет 18.0÷71.0 м, высота сечения 2.5÷8.5 м. Со стороны противоположной полю, полуарки опираются шарнирно на железобетонный каркас подтрибунных помещений на шарнирно неподвижную опорную часть. Шарнирно неподвижная опорная часть (3 степени свободы) обеспечивает поворот опорных узлов полуарок в 3-х плоскостях с коэффициентом трения не более 3% при расчетной температуре наружного воздуха наиболее холодной пятидневки.

Нагрузки от кровли передаются на основные арки и полуарки через систему плоских ферм ФП1…ФП6, расположенных в перпендикулярном направлении к полуаркам с шагом 12.0 м и ферм ФС1…ФС18, опирающихся на фермы ФП и расположенных в перпендикулярном направлении к ним с шагом 9.0 м (рисунок 2).

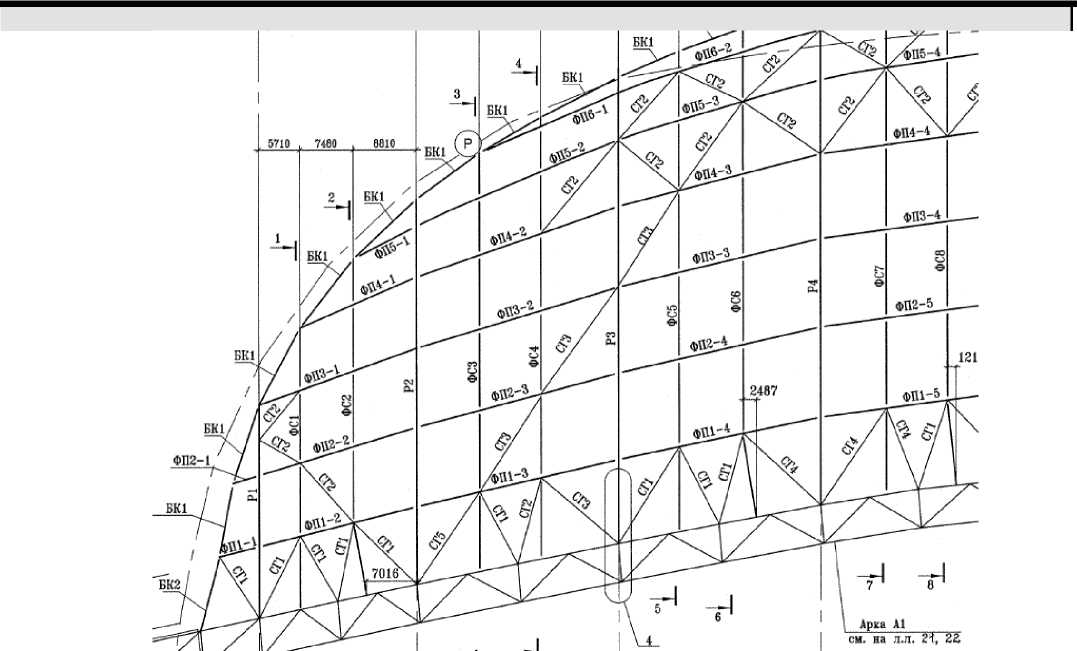
Рисунок 2. Фрагмент схемы расположения несущих конструкций покрытия

В качестве сечений элементов покрытия стадиона используются сварные коробчатые и сварные двутавровые сечения. Материал стальных конструкций – сталь марки С390 толщиной до 50мм и сталь марки С345 толщиной до 120 мм.

Ограждающие конструкции покрытия выполнены из мембранной светопрозрачной конструкции из полимера ETFE.

Создание КЭ модели расчетной схемы в SCAD

Рассматриваемый объект является уникальным сооружением со сложной конструктивной схемой, состоящей из большого числа элементов. Уровень ответственности 1а (коэффициент надежности по ответственности ( Yn = 1.2 ). Традиционные способы создания расчетных моделей посредством ввода узлов и элементов будут невыгодно отличаться значительной трудоемкостью и вероятностью появления субъективных ошибок, поскольку конструкции расположены относительно друг друга в разных плоскостях и под разными углами и имеют более 3000 узлов. Для устранения этих факторов решено использовать следующие возможности программы [5]:

• -  импорт геометрии системы из программы «AutoCAD»;

• -  прочтение данных из текстового файла;

• -  режим сборки.

Покрытие моделировалось по имеющейся проектной документации, выполненной ГУП МНИИП Моспроект-4 и ООО «ГК-ТЕХСТРОЙ».

Выделены следующие группы элементов конструкции покрытия:  главная арка, полуарки, вспомогательные фермы, ограждающие конструкции. Алгоритм создания расчетной модели приведен на рисунке 3.

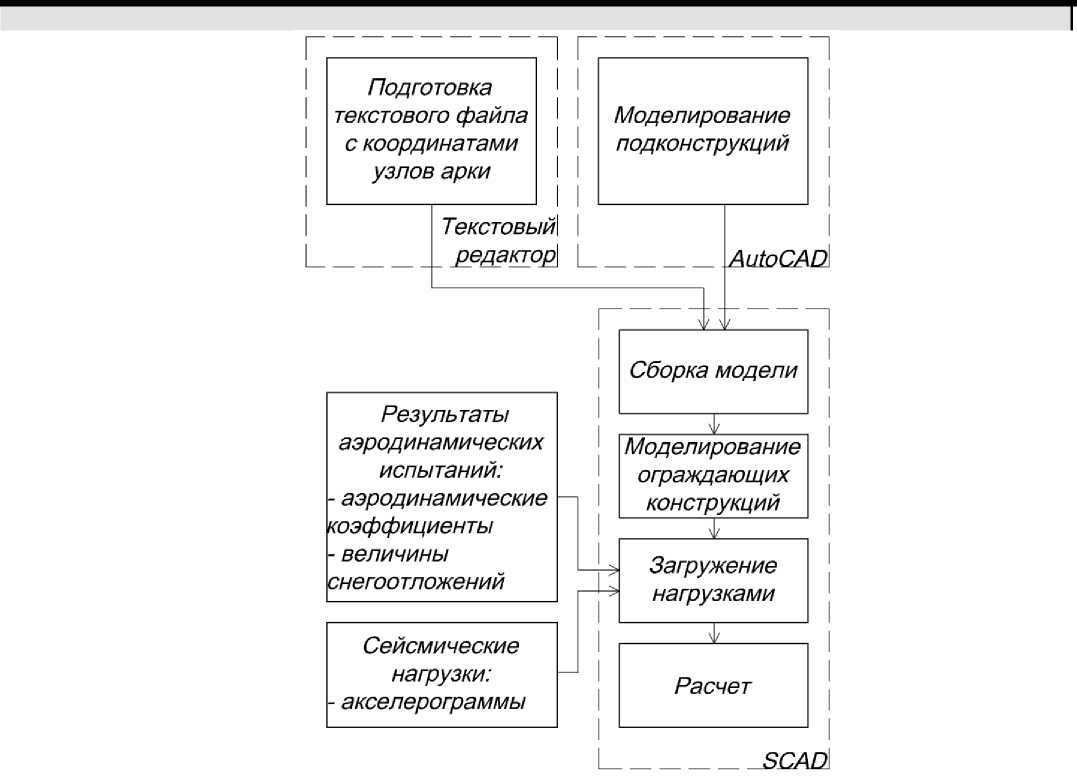
Рисунок 3. Схема алгоритма создания расчетной модели

В результате в среде SCAD получена модель, показанная на рисунке 4, где красным цветом выделена главная арка.

Рисунок 4. Конечно-элементная модель расчетной схемы

Характеристика нагрузок и расчет

На пространственный каркас действуют постоянные нагрузки – от веса ограждающих и несущих конструкций здания, временные – атмосферные (снег и ветер) и кратковременные – технологические, температурные, а также особая – сейсмическая нагрузка.

Собственный вес конструкций был задан автоматически при помощи функции задания собственного веса. Технологические нагрузки были приложены на соответствующие узлы и элементы согласно схеме нагрузок.

Снеговая нагрузка вычислялась по [1] и прикладывалась к ограждающим элементам покрытия. Рассматривалось 3 варианта снегового загружения: с равномерным расположением снега по всему покрытию и «треугольным» по каждой половине покрытия.

Ввиду отсутствия в отечественных нормативных документах схем ветрового загружения для подобных сооружений, ветровая нагрузка расчитывалась по европейским нормам [2] и прикладывалась на ограждающие элементы по 4 направлениям (север, юг, запад, восток).

Температурные нагрузки были расчитаны по [1], проверены при помощи сателлита «ВеСТ» и приложены на несущие элементы отдельно для летнего и зимнего времен года.

В рамках выполнения исследовательской ВКР сейсмические нагрузки не учитывались.

Расчетные сочетания усилий были заданы автоматически в зависимости от типа загружения и вида нагрузки, после чего был произведен статический расчет схемы.

Анализ напряженно-деформированного состояния элементов основной арки покрытия

Для исследования напряженно-деформированного состояния покрытия были отобраны наиболее нагруженные элементы главной арки, как основной несущей конструкции. Для этих элементов были посчитаны напряжения от продольного усилия N и изгибающих моментов в двух плоскостях М_у и M_z (таблица 1).

a — a _N + о _Му + a _Mz

Таблица 1. Значения напряжений от различных силовых факторов для элементов главной арки

№	N , кН	A, см2	, МПа	%	My ,кН м	И у , см³	^My, МПа	%	Mz , кНм	Wz , см³	^Mz , МПа	%
46	19342	544,3	355,4	81	313	7704,5	40,63	9	315	7413,2	42,5	10
50	19549	544,3	359,2	83	376	7704,5	48,80	11	177	7413,2	23,9	6
61	14016	1248,0	112,3	84	328	31369	10,46	8	296	27173, 6	10,9	8
76	18830	544,3	345,9	80	345	7704,5	44,78	10	299	7413,2	40,3	9
79	10126	544,3	186,0	81	168	7704,5	21,81	9	165	7413,2	22,3	10
81	9623	300,0	320,8	96	59	4654,4	12,68	4	0	1688,6	0,0	0
88	18913	544,3	347,5	82	355	7704,5	46,08	11	241	7413,2	32,5	8
91	15026	544,3	276,1	86	242	7704,5	31,41	10	106	7413,2	14,3	4
97	4344	544,3	79,8	89	22	7704,5	2,86	3	54	7413,2	7,3	8
104	11943	544,3	219,4	81	242	7704,5	31,41	12	140	7413,2	18,9	7
112	4364	300,0	145,5	92	59	4654,4	12,68	8	0	1688,6	0,0	0
117	4315	300,0	143,8	98	14	4654,4	3,01	2	0	1688,6	0,0	0
121	7852	544,3	144,3	79	165	7704,5	21,42	12	129	7413,2	17,4	10
126	12985	544,3	238,6	84	172	7704,5	22,32	8	170	7413,2	22,9	8
129	3978	300,0	132,6	91	60	4654,4	12,89	9	0	1688,6	0,0	0
Сред.				86				8				6

Construction of Unique Buildings and Structures, 2014, №2 (17)

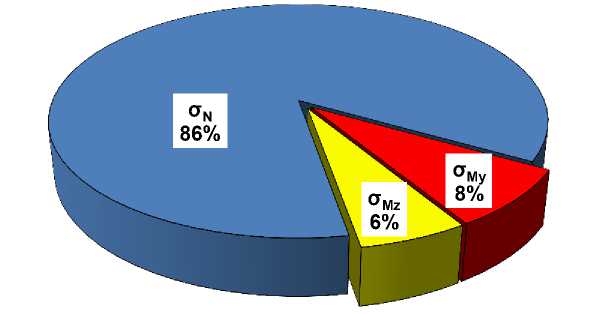
Рисунок 5. Диаграмма соотношения между напряжениями для элементов главной арки

Как видно из рисунка 5 наибольший вклад (86%) в значения нормальных напряжений вносит составляющая от продольного усилия N .

В указанных элементах проведен анализ O_N , возникающих от различных загружений (таблица 3).

Таблица 2. Составляющие О эд от отдельных загружений

№ элемента	Вид нагрузки
	Постоянная		Снеговая		Ветровая		Температурная
	Значение, кН	%	Значение, кН	%	Значение, кН	%	Значение, кН	%
46	-25894,0	65	-2178,4	5	603,3	2	11161,0	28
50	-17182,1	80	-2057,5	10	985,6	5	1386,4	6
61	-19738,9	63	-3291,9	10	1496,6	5	-7025,1	22
76	-12010,2	57	-1716,2	8	923,6	4	-6559,2	31
79	-25897,2	72	-2696,9	8	1335,9	4	-5888,7	16
81	-5110,6	31	535,4	3	-849,7	5	-10186,8	61
88	-12965,1	75	-1925,8	11	535,4	3	-1842,1	11
91	-12608,1	77	-1944,8	12	870,3	5	897,0	5
97	-7733,9	52	-1162,4	8	646,3	4	5283,2	36
104	-13630,9	66	-1724,3	8	907,9	4	4280,3	21
112	-16588,3	74	-2011,1	9	967,3	4	3000,7	13
117	-13539,2	75	-1929,3	11	1032,0	6	1440,5	8
121	-3601,7	68	-573,1	11	-79,8	2	1028,3	19
126	-14953,1	54	-2704,5	10	1241,2	5	-8601,0	31
129	-14953,1	54	-3342,0	12	1500,9	5	-7897,5	29
Среднее		64		9		4		23

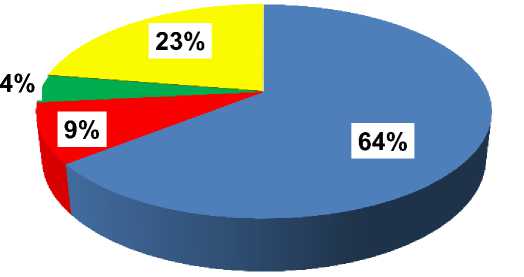
■ Постоянная

■ Снеговая

■ Ветровая

Температурная

Рисунок 6. Диаграмма соотношений усредненных значений а^ от отдельных загружений

Результаты показывают, что основной вклад в напряженное состояние элементов главной арки принадлежит нагрузке от собственного веса (почти 65%). При этом следует отметить существенную долю (23%) влияния температурных воздействий.

Выбор целевой функции для решения задач оптимального проектирования

Исходя из особенностей расчета и проектирования, а также учитывая практические вопросы, можно сформулировать одну из основных задач оптимального проектирования металлических конструкций: определить оптимальные геометрические параметры статически неопределимой системы при условии введения в лишние связи начальных усилий.

Проблемы оптимизации металлических конструкций освещены в работах Лихтарникова Я.М. [21], Холопова И.С. [22-24] и ряда других авторов [40, 41]. В общем случае, решение таких задач является весьма сложным, что обуславливается нелинейностью их постановки и определенными трудностями математического описания. Если исходить из тех же критериев и ограничений, которые обычно принимаются при решении задач оптимального проектирования конструкций, то нетрудно убедиться в том, что целевая функция в рассматриваемом случае принимает нелинейную форму. Обычно под целевой функцией понимают выражение объема, массы или стоимости материала конструкции, записанные в зависимости от неизвестных задачи [8].

В процессе исследования оценивалась металлоемкость главной арки и всей конструкции покрытия.

Для вычисления фактической металлоемкости расчетных моделей, необходимо было произвести не только расчет, но и подбор сечений в каждой из полученных схем, включающих в себя около 3000 элементов каждая. В связи с огромным объемом необходимых вычислений, для упрощения задачи сравнения были приняты следующие гипотезы:

• -    Соотношение жесткостей от схемы к схеме меняется незначительно. Следовательно, можно считать, что соотношение жесткостей исходной схемы дает достаточно (для вариантного анализа) достоверную картину распределения усилий по элементам.

• -    Основным силовым фактором во всех элементах схемы является осевое продольное усилие N . Следовательно, площади сечений элементов будут напрямую зависеть от продольных усилий, возникающих в них.

• -    Все элементы конструкции выполнены из стали с одинаковыми механическими характеристиками.

Произведение продольного усилия в i-м элементе на длину элемента Nt ∙к для каждого элемента будет прямо пропорционально объему нетто i-го элемента Vt =   ∙к , а следовательно и его массе mt =  ∙p. Сумма произведений ∑ Nt ∙к (назовем ее условной металлоемкостью) всех элементов будет прямо пропорциональна металлоемкости расчетной модели и может быть принята в качестве целевой функции сравнения вариантов расчетных моделей.

Алгоритм подсчета условной металлоемкости покрытия

Для подсчета значений целевых функций элементов покрытия был использован режим «Документирование» SCAD с последующей обработкой результатов отчета в среде MS Excel (рисунок 7).

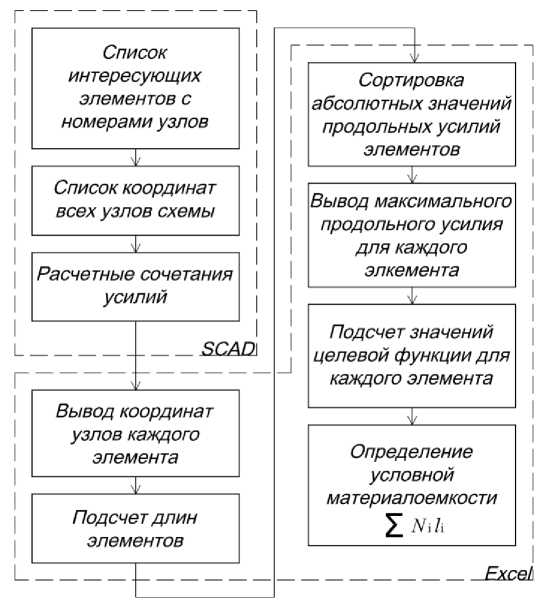
Рисунок 7. Схема алгоритма определения условной металлоемкости

К основным достоинствам приведенного алгоритма стоит отнести высокую степень автоматизации процесса и, как следствие, высокую скорость расчета и сведение к минимуму ошибок вычисления. Фрагмент таблицы с расчетом приведен на рисунке 8.

	А	в	С        D        Е	F	6	Н 1        1	J	к	L        М       N
1	Элементы
2	Параметры выборки:								12690425
3	Списокузлов/элементов: 1-232 235-852 855-2389 2391 2393-2563 2811-2815 2820-2846 2889-2897 2990-3113 3163-3287
4	Номер эле	Тип элеме	Тип жесткУзлы	Х1	у!	zl        х2	У2	z2	Длина, м Усилие, Т NL, т*м
5	1	5	5  12	-143,088	17,793	12,446 -136,013	19,318	16,311	8,204845 3016,39 24749,01
6	2	5	5         2         3	-136,013	19,318	16,311 -127,721	21,106	20,84	9,615927 2157,082 20742,34
7	3	5	5         3         4	-127,721	21,106	20,84 -119,58	22,86	25,288	9,441245 1926,165 18185,4
8	4	5	5         4         5	-119,58	22,86	25,288 -108,628	25,218	31,258	12,69438   2347,6 29801,33

Рисунок 8. Фрагмент расчетной таблицы для определения условной металлоемкости схемы

1. Элементы 2. Координаты и связи 3 "Новые РСУ" с автоматически

Поиск рациональной геометрической схемы конструкций покрытия

В процессе исследовательской части работы были поставлены и решены две следующие задачи:

• 1.    Поиск рациональной схемы сооружения при изменении расстояния между поясами главной арки при неизменной геометрии верхнего пояса.

• 2.    Поиск рациональной схемы при изменении высоты главной арки с сохранением математического подобия формы.

Анализ моделей покрытия производился путем сравнения их условной металлоемкости.

Первоначально был произведен анализ металлоемкости главной арки по отношению к металлоемкости всего покрытия. Так, согласно пробным вычислениям, подтвердившимся в результате исследования, металлоемкость главной арки составляет 50% от металлоемкости всей конструкции.

Задача 1 – Изменение расстояния между поясами путем смещения нижнего пояса главной арки

Созданы модели несущих конструкций покрытия, отличающиеся от оригинальной положением нижнего пояса главной арки. Модели были созданы по следующим критериям:

• -    сечение главной арки продолжает представлять собой прямоугольник с 4 поясами по углам;

• -    высота сечения главной арки на опорах остается неизменной;

• -    положение верхнего пояса арки остается неизменным;

• -    угол наклона арки остается неизменным.

Для первоначального анализа создавалось 9 моделей. При этом стрела подъема нижнего пояса f варьировалась от 0.9 fo до 1.125 fo с шагом 0,025 fo , где fo = 53.04 м – стрела подъема нижнего пояса арки в изначальной схеме.

Схема нижнего пояса была сохранена 16 раз в виде отдельных подсхем, каждая из которых впоследствии была соединена с оставшейся частью модели при помощи режима сборки. При этом несовпадающие узлы элементов нижнего пояса и раскосов соединялись вручную при помощи инструмента «Замена узлов в элементах» [5].

Для всех полученных моделей были посчитаны значения условной металлоемкости, по которым впоследствии был построен график (рисунок 9). В интервалах появления локальных экстремумов частота шага изменения параметров оптимизации уменьшалась с целью уточнения точки экстремума.

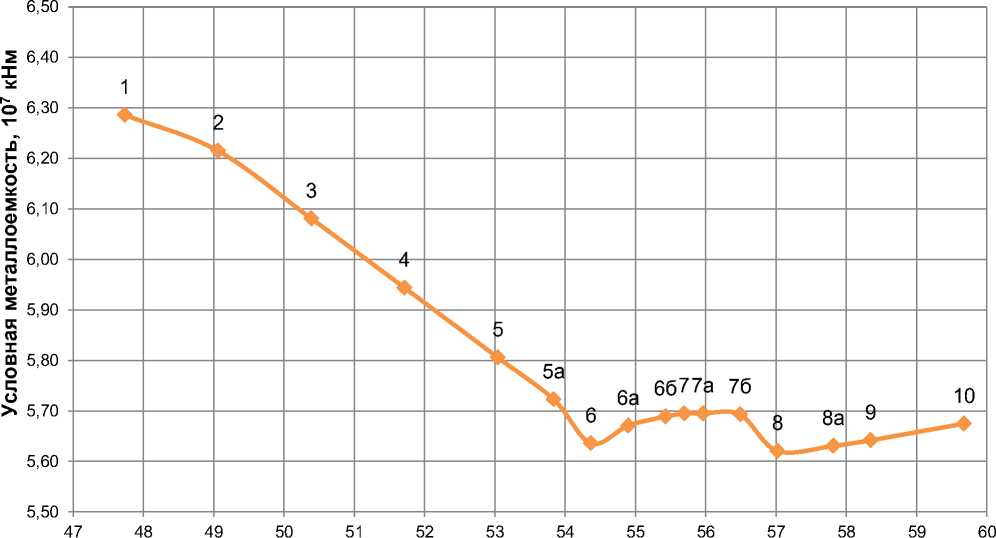
Стрела подъема нижнего пояса арки, м

Рисунок 9. График зависимости условной металлоемкости главной арки от стрелы подъема нижнего пояса

Для каждой из 16 моделей были так же собраны данные по условной металлоемкости всей схемы (таблица 3). По полученным данным был построен окончательный график (рисунок 11).

Таблица 3. Расчет условной металлоемкости для задачи 1

No. модели	£ /о	г , м	∑ Nt ∙ к главной арки, 107 кН∙м	∑ Nt ∙ It всего покрытия,107 кН∙м	Доля ∑ Nt ∙ It главной арки от ∑ Nt ∙ li всего покрытия
1	0,900	47,74	6,29	12,31	0,51
2	0,925	49,06	6,22	12,29	0,51
3	0,950	50,39	6,08	12,18	0,50
4	0,975	51,71	5,94	12,02	0,49
5*	1,000	53,04	5,81	11,76	0,49
5а	1,015	53,84	5,72	11,55	0,50
6	1,025	54,37	5,64	11,36	0,50
6а	1,035	54,90	5,67	11,19	0,51
6б	1,045	55,43	5,69	11,06	0,51
7	1,050	55,69	5,70	11,01	0,52
7а	1,055	55,96	5,70	10,98	0,52
7б	1,065	56,49	5,69	11,00	0,51
8	1,075	57,02	5,62	11,11	0,51
8а	1,090	57,81	5,63	11,31	0,50
9	1,100	58,34	5,64	11,43	0,49
10	1,125	59,67	5,68	11,67	0,49

*Примечание: исходная схема.

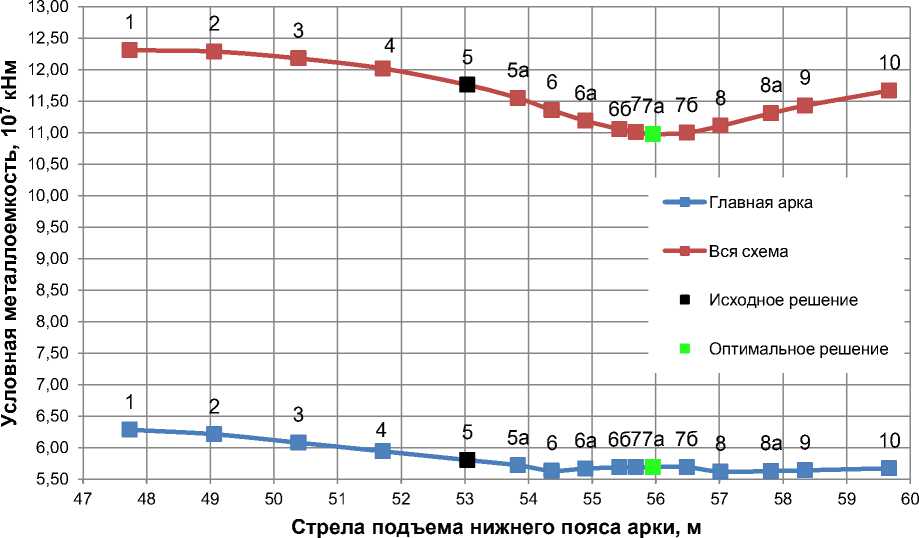
Рисунок 10. Графики зависимости условной металлоемкости от стрелы подъема нижнего пояса для главной арки (снизу) и всего покрытия (сверху)

В точке 7а зафиксирован локальный максимум целевой функции для главной арки. В районе этой же точки зафиксировано наименьшее значение целевой функции для всей схемы. Таким образом, схему 7а можно с учетом принятых допущений считать оптимальным решением геометрической схемы конструкции в рамках решаемой задачи. Полученная условная металлоемкость ниже условной металлоемкости исходной схемы на 6%.

Задача 2 – Изменение высоты подъема стрелы арки

Для анализа поставленной задачи были созданы модели несущих конструкций покрытия, отличающиеся от оригинальной масштабом в направлении вертикальной оси Z.

Было создано 16 моделей. При этом стрела подъема нижнего пояса f варьировалась от 0.9 fo до 1.1 /о (с шагом 0,025 /о), где fo = 53.04 м – стрела подъема нижнего пояса арки в изначальной схеме.

Расчетные модели создавались с использованием SCAD при помощи инструмента «Геометрические преобразования» [5]. Вся схема нижнего пояса была масштабирована и сохранена 16 раз в виде отдельных подсхем.

Для всех полученных моделей были посчитаны значения условной металлоемкости (таблица 4), по которым впоследствии был построен график (рисунок 11). Все операции по построению зависимостей аналогичны задаче 1.

Таблица 4. Расчет условной металлоемкости для задачи 2

No. модели	f /о	г , м	∑ Nt ∙ It главной арки, 107 кН∙м	∑ Nt ∙ It всего покрытия,107 кН∙м	Доля ∑ Nt ∙ It главной арки от ∑ Nt ∙ It всего покрытия
10	0,600	31,82	5,21	10,09	0,52
11	0,700	37,13	5,26	10,23	0,51
12	0,800	42,43	5,51	10,34	0,53
13	0,825	43,76	5,52	-	-
14	0,850	45,08	5,51	10,55	0,52
15	0,875	46,41	5,49	-	-
1	0,900	47,74	5,53	10,92	0,51
2	0,925	49,06	5,56	-	-
3	0,950	50,39	5,59	11,25	0,50
4	0,975	51,71	5,72	-	-
5	1,000	53,04	5,81	11,76	0,49
6	1,025	54,37	5,89	-	-
7	1,050	55,69	5,99	12,20	0,49
8	1,075	57,02	6,07	-	-
9	1,100	58,34	6,13	12,52	0,49

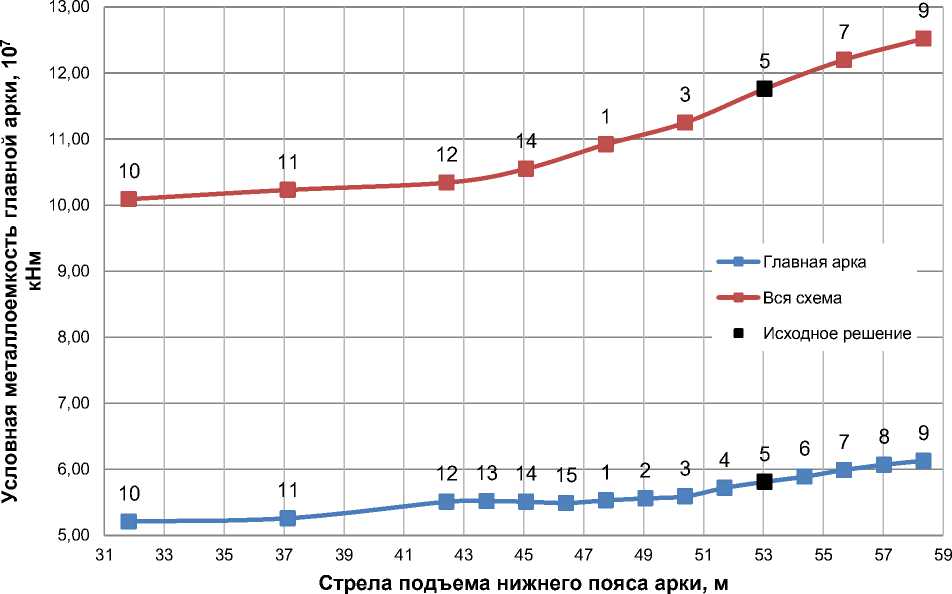
Рисунок 11. Графики зависимости условной металлоемкости от стрелы подъема нижнего пояса для главной арки (снизу) и всего покрытия (сверху)

Обнаружить экстремумы в результате исследования не удалось. Значение целевой функции уменьшается при снижении общей высоты схемы. Признать какой-либо из рассмотренных вариантов оптимальным не представляется возможным. При определении высоты сооружения решающими оказались не конструктивные ограничения, а архитектурные и технологические.

Выводы

• 1.    Выполнено создание КЭ модели расчетной схемы несущих металлических конструкций покрытия стадиона Фишт с использованием SCAD совместно с другими современными программными комплексами.

• 2.    Произведен анализ напряженно-деформированного состояния элементов главной арки покрытия на различные нагрузки и воздействия. Структурный анализ состава напряжений в наиболее нагруженных элементах показал, что наибольшие напряжения возникают от собственного веса (более 65% от максимальных), а основным силовым фактором в стержневых элементах является продольное усилие N .

• 3.    Предложен метод сравнения рациональности вариантов расчетных схем по критерию их условной металлоемкости. Разработан алгоритм расчета значения целевой функции, отличающийся высокой степенью автоматизации и, как следствие, скоростью и точностью расчета.

• 4.    При помощи предложенного алгоритма решены две задачи по поиску рационального решения методом вариантного проектирования. При вариантном проектировании поиска расстояния между поясами главной арки (первая задача) обнаружен глобальный минимум значения целевой функции, отличающийся на 6% от проектного решения и свидетельствующий о наиболее оптимальном варианте расчетной схемы в рамках принятых допущений. При исследовании влияния высоты сооружения на его металлоемкость (вторая задача) определить наиболее рациональное решение, ограничиваясь лишь критерием условной металлоемкости, не удалось.