Поиск в модели газовых месторождений максимальной длины их общей "полки"
Автор: Скиба А.К.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 2 (42) т.11, 2019 года.
Бесплатный доступ
Рассматривается непрерывная агрегированная динамическая модель группы газовых месторождений. Ставится и решается задача максимизации длины общей «полки» газовых месторождений. Предлагаемые к исследованию задачи относятся к классу задач оптимального управления со смешанными ограничениями с нефиксированным временем и подвижным правым концом. Основным математическим аппаратом является принцип максимума Понтрягина в форме Эрроу, в котором используются множители Лагранжа. Полученные результаты анализируются.
Оптимальное управление, предложение к. эрроу, модель газовых месторождений, нефиксированное время, подвижный правый конец
Короткий адрес: https://sciup.org/142220488
IDR: 142220488 | УДК: 519.86
Текст научной статьи Поиск в модели газовых месторождений максимальной длины их общей "полки"
Наша, страна. - одна, из богатейших стран мира, по имеющимся природным ресурсам и полезным ископаемым. Среди обширного их перечня особое место занимает природный газ. Россия является ведущей державой в мире по добыче, запасам и ресурсам газа. Она. обеспечивает свыше 21% его мирового производства и около 25% всех международных поставок.
По своим характеристикам природный газ относится к невосполнимых полезных ископаемых, находящихся в недрах Земли при высоком давлении и температуре. Природный газ в пласте содержится в газообразном состоянии в виде отдельных скоплений (газовых месторождений) на. глубине от 250 метров до 10 километров. В состав природного газа, входят много полезных веществ, используемых в быту и в промышленности.
Для вскрытия продуктивного пласта, и извлечения из него голубого топлива, используют скважины. Скважины стараются разместить равномерно по всей территории месторождения. Это делается с целью по возможности обеспечить равномерное падение пластового давления в процессе извлечения природного газа, из залежи [1].
Природный газ экологически чистый ценный продукт, спрос на который велик. В нем заинтересованы как отечественные, так и зарубежные потребители. Россия по имеющимся доказанным запасам в состоянии обеспечить огромный спрос в газе в течение длительного периода времени. Однако места добычи газа и потребления газа находятся на значительном расстоянии. Один из самых эффективных способов доставки газа — это его транспортировка по газопроводу.
Объемы пропускаемого по трубопроводу газа ограничиваются его текущей пропускной способностью Q. Перед газовиками на месторождениях стоит ряд задач. Самой главной по важности задачей является выполнение в данный момент текущей добычи, равной значению Q. Если в момент t справедливо строгое неравенство
п
Е ф(№ >Q, (1)
г =1
то существуют такие N = N Е [0, N, при которых выполнено равенство
п
Е <М = Q, (2)
г =1
где п - число газовых месторождений в группе; N - общий фонд добывающих скважин на г-м месторождении; N - действующий фонд дсбывающих скважин на г-м месторождении; q i (t) - среднедействующий де бит скважины в момент t на г-м месторождении.
Таких решений, удовлетворяющих равенству (2), достаточно много. Поэтому на этом множестве можно решать как статические, так и динамические задачи. Поскольку по мере разработки месторождения дебит скважины убывает, наступает момент Т, при котором выполняется равенство п
£ q i (T)N = Q . (3)
г =1
В следующий момент план по добыче газа уже не выполняется. Величина Т называется длиной «полки» группы месторождений при рассматриваемой стратегии ее разработки. Возникает вопрос: в каких пределах может находиться длина «полки» группы месторождений? Для этого необходимо решить задачи оптимального управления со смешанным ограничением на максимум и на минимум. В настоящей работе мы ограничимся решением только одной задачи на максимум. В качестве основного математического аппарата выбираем принцип максимума Понтрягина в форме Эрроу.
2. Принцип максимума Понтрягина в форме Эрроу
Во второй половине прошлого столетия была опубликована статья К. Эрроу [2], ставшего впоследствии лауреатом Нобелевской премии по экономике. В основе работы лежит принцип максимума Понтрягина [3]. К. Эрроу модифицирует принцип и формулирует предложения, которые позволяют решать задачи оптимального управления со смешанными ограничениями. В предложения дополнительно включены некоторые элементы нелинейного программирования, такие, как лагранжиан, множители Лагранжа и условия дополняющей нежесткости. Автор настоящей статьи использовал модифицированный принцип в работе [4].
Среди других работ по оптимальному управлению следует обратить внимание на монографии А.М. Тер-Крикорова [5], С.М. Асеева и А. В. Кряжемского [6]. Заслуживает интерес работа Е. Болдера [7], посвященная теореме существования решения задачи оптимального управления на бесконечности.
Сформулируем предложения К. Эрроу.
Предложение 1. Пусть v(t) - управления (0 6 t 6 Т ), максимизирующие функционал
/т
и [x(t),v(t),t]
dt
при условии to
x = G[x(t), v(t), t], ограничениях на управления
(Ь)
F[x(t),v(t),t] > О, которые, возможно, включают переменные состояния, начальных условиях на переменные состояния и граничных условиях
х(Т ) > 0.
Если условия регулярности выполнено, то существуют сопряженные переменные p(t), такие, что для каждого момента 1
-
(с) v(t) максимизирует Н [x(t), v,p(t), t] относительно ограничений (Ь), где
Н (x,v,p,t) = И (x,v,t) + pG(x,x,t);
-
(d) p = —QL/Qxi при x = x(t), x(t) = x(t), p = p(t), где
-
(e) L(x,v,p,q,t) = Н (x,v,p,t) + qF (x,v,t),
и множители Лагранжа q, такие, что
(f) dL/dx>k = 0 при x = x(t), ^(t) = x(t), p = p(t),
3. Описание модели и постановка задачи
q > 0, qF [x(t), v(t), t] = 0.
В предложении 1 вектор x(t) имеет размерность п, а вектор v(t) - размерность т.
Перейдем к описанию модели и постановки задач.
Рассмотрим модель функционирования группы газовых месторождений с взаимовлия-ющими скважинами [8, 9]. Пусть V i — извлекаемый запас на Ум месторождении.
Между переменными устанавливается дифференциальная взаимосвязь, которую опишем в виде системы дифференциальных уравнений:
q0
^ = -Niqi, qi = - ^:0 qi(t)Ni(t), г = 1,п, при начальных условиях V)0 > 0, q" > 0. На фонд действующих скважин накладывает-
_^_
_^_
ся следующее ограничение: 0 6 N 6 N Здесь Ni > 0. Считается, что все добывающие скважины равномерно распределены по площади каждого месторождения. Это является одним из основных предположений при построении модели. Предполагаем также различ-70
ными между собой величины ^Мг.
v г
Задача 1. О максимизации длины общей «полки» для группы газовых месторождений.
Требуется максимизировать функционал Т —> max при дифференциальных связях:
qi = -a0qi(t)Ni(t),
г = 1, п,
начальных условиях q0 > 0, г = !,п,(5)
и ограничениях на управления вдоль траектории
0 6 Ni(t) 6 Ni, г = 1,п,(6)
п
Е qi(t)Ni(t) = Q,(7)
i =1
где 0 0 _ Чг j ох ai •
Г i
Предполагаем, что начальные условия удовлетворяют строгому неравенству:
п
Е 9 0 N > Q. (9)
i =1
Управления N(t),z = 1,п принадлежат множеству измеримых функций.
Справедливы следующие утверждения.
Утверждение 1. Для любой допустимой траектории из множества (4), (8), (9) выполняется строгое неравенство q i (T ) > 0, г = 1,п.
Данное утверждение вытекает из дифференциальных уравнений (4), начальных условий (8) и ограничениях на управления (9).
Утверждение 2. Для любой допустимой траектории из множества (4), (8), (9), (11) при начальном ограничении (9) существует такое T > 0, при котором выполняется равенство п
Е q i (T)N i = Q. (10)
i =1
Точка q(T ) является концом допустимой траектории q(t). Дальнейшее развитие системы (4) невозможно из-за имеющихся ограничений.
Доказательство.
Умножим обе части каждого дифференциального уравнения (4) на соответствующую величину N», просуммируем, и далее обе части проинтегрируем. После несложных преобразований получаем п п
Е qi(t)N = Е q^i i=1 i=1
-
п
Е^м i=1
t j qi(t)Ni(t) dt.
(И)
С учетом (И) продолжим преобразование п п
Е q i (t)N i = Е q№ i =1 i =1
-a^Qt - Е (a0N i =2
-
а?М) J 0
q i (t)N i (f) dt.
Пусть a^Ni имеет наименьшее значение среди остальных величин a0Ni, г = 2,п, тогда п п
Е q^N i < Е q^ i - a° i N i Qt. i =1 i =1
Правая часть неравенства (13) за конечное время t‘ достигает значения Q. Отсюда вытекает, что левая часть того же неравенства достигает значения Q за время T Е (0,t‘). Таким образом, в момент T выполняется равенство (10).
Утверждение 3. Пусть на некоторой траектории в некоторый момент Т выполняется равенство (10), тогда
п
Е
q
,
(t)V
,
(14)
г =1
при Т < t.
Данное утверждение очевидно.
Из утверждений 2 и 3 вытекает следующее утверждение.
Утверждение 4. Для любой допустимой траектории с нефиксированным временем из множества (4), (8), (9), (11) при начальном ограничении (9) управление на правом конце строго определено, т.е. V , (Т ) = V , , г = 1,п.
Перед газовиками на месторождениях стоит первоочередная задача - выполнение в каждый текущий момент t плана по совокупной добыче, равной Q. Невыполнение плана может привести к ряду отрицательных последствий, например, к крупным штрафным санкциям или к отзыву лицензии. В начальный момент t = 0 множество решений V, из равенства (2) достаточно широкое. Для выбора конкретного значения V, решаются статические или динамические задачи. Со временем множество решений V, сужается, а дополнительные задачи меняются. Наступает момент t = Т, когда множество решений V, состоит только из одной точки V,. Далее вследствие утверждения 3 процесс прерывается.
В связи с этим возникает задача нахождения максимума значений Т на множестве всех допустимых траекторий. Можно дать грубую верхнею оценку этого максимума. Данная Уп_ V° оценка равна г=1 1 . Эту оценку можно получить напрямую из модели при условии отсутствия ограничения (9).
Переформулируем постановку задачи 1.
Задача 1а. О максимизации длины общей «полки» для группы газовых месторождений.
Требуется найти такое оптимальное управление V,, г = 1,п, динамической системы (4) из класса допустимых управлений, переводящее динамическую систему из заданного начального состояния (8) в гиперплоскость (10) за максимальное время Т при ограничениях на фазовые переменные и управления вдоль траектории (9), (11).
Предполагаем, что начальные условия удовлетворяют строгому неравенству (9). Управления V,(t), г = 1,п, принадлежат множеству измеримых функций.
Оптимальное решение для рассматриваемой задачи существует. Это, например, следует из монографии [10].
Задача 1а является задачей оптимального управления с подвижным правым концом и нефиксированным временем.
Для решения задачи 1а мы будем пользоваться предложением К. Эрроу и соответствующими условиями трансверсальности. Применяемые ниже условия трансверсальности не упоминаются в работе [2] вместе с предложениями К. Эрроу. Тем не менее они используются при решении соответствующих задач оптимального управления вместе с принципом максимума Понтрягина в классической формулировке [11].
4. Исследование задачи 1а
Напомним, л®
«, , г = 1,п. (15)
Далее упорядочим фазовые переменные в порядке возрастания величин а,V,. Заметим, что такой порядок единственный, поскольку согласно условиям в постановке задачи различны величины «V.;. г г
Согласно предложению 1, выпишем гамильтониан и лагранжиан:
п
Н (q ,N, 3) = 1 - ^ -1^0 0 q i N t , i=1
L(q, N, ф, ^ЛЗ) = 1 + £[-фіа0 qiN + ^г(Ж - Ni) + 8iNi] + i=1
+3£(qiNi) - Q]. (17)
i=1
Далее опишем множество G(q) допустимых управлений, на котором осуществляется максимизация гамильтониана (16):
G(q) = {N G Rn | 0 6 N 6 N , f^ q i N i = Q}. (18)
i =1
Основная цель исследования заключается в поиске на основании предложения 1 вектор-функций ФО) и управлений N(t), которые удовлетворяют приведенной ниже сопряженной системе дифференциальных уравнений (22), условиям трансверсальности:
п
Н(q(T),N(T),ф(Т )) = 1 - £ ф г (Т)a 0 q i (Т)N i = 0, (19)
i=1
Ф і (Т ) = vN i , г = 1^, (20)
где и - некоторое число, и при каждом t G [0,Т] управления N(t) максимизируют гамильтониан:
Н (q(t),N(t),3(t)) = N max)^ ( q (t') ,N,ф (t')') =
п
= max
N £G ( q ( t ))
i =1
- a i ^ i (t)q i (t)N i ].
Система сопряженных уравнений представится в виде фг(t) = -dL/dqi = а^фг(t)Ni(t) - 3(t)Ni(t), г = 1,n, или в более удобной форме:
■фг (t) = [а° ф г (t) - 3(t)]N7i (t), г = 1, n.
Согласно предложению 1 множители Лагранжа 3(t),y(€),6(£) должны удовлетворять равенствам dL/dNi = -0фг(t)qi(t) + 3(t)qi(t) - ^i(t) + 8г(t) = 0, г = 1,n,
|
ИЛИ |
-qi ( t )[ ai ф г ( t ) -3(t)]=7i ( t ) - 8i(t), г = 1 ,n ; (23) 3(t)[i2 q i (t)N^ i (t) -Q]=0; (24) i=1 7i(t)[Wi -TVi(t)]=0, 7i(t) > 0, г = 1П; (25) |
8 г (t)N i (t) = 0, 8 г (t) > 0, г = 1,n.
Введем обозначения ^i(t) = a0^i(t), г = 1,п. В новых обозначениях максимизация гамильтониана (21), система сопряженных уравнений (22), равенство (23), условия трансверсальности (19) и (20) перепишутся в следующем виде:
Н(q(t),N (t), = n ты Н(q(t), N, = = 1+ max V\-Pi(t)qi(t)Ni]. (27) n^GW ^=1 Vi(t) = \pi(t) - /3(t)]a0Ni(t), г = 1,п; (28) qi(t)\ i(t) - /3(t)] = 5i(t - ^i(t), г = 1,п. (29) Н(q(T),N(T),V(T)) = 1 - ^2 Vi(T)qi(T)N? = 0, (30) i=1 ^i(T)=va0TVi, г = 1,п. (31) Из (19) и (20) получаем, что правый конец сопряженной траектории -^(t) лежит в положительной области. Воспользовавшись условиями трансверсальности (19) и (20), с учетом (30), (31), полу- чаем v EbiOW )N' 11,21 Vi(T) = En a\N‘ ,.2• г = ІТ5. (3» i=ia0q?(T )N2 **(T ) = Eli.?^ (T )Nr г = 1,". 1341 Отсюда следует утверждение. Утверждение 5. Правый конец «сопряженной» вектор-функции y(t) лежит в положительной области, т.е. ^i(T) > 0, г = 1,п. Значения компонент вектора ^i(T), г = 1,п, расположены в возрастающем порядке. Если бы мы знали значение вектора q^(T), то коэффициент v и соответственно значения векторов <ДТ) и ^(Т) также были бы определены. В противном случае можно получить только их оценки: 1 // 1 . a°nNnQ - V - У.Ү.О; а? V O N? г = 1, п; — — Ni „ , Ni a°nNnQ - ^i( ) - qONiQ, г = 1, п. Теорема 1. Пусть фазовые переменные q?(t) упорядочены в порядке возрастания величин а?Ni, тогда (1) оптимальная траектория вычисляется в каждый момент t Е \0,T] по формулам t qi(t) = q0 exp\-а0j Ni(6) de], г = 1, п; (2) вектор оптимальных управлений N(t) однозначно определяется в соответствии со следующим правилом. Для каждого t существует такое целое число k Е {1,..., п}, при котором выполняется двойное неравенство Vk' 1qi(t)Ni < Q 6 XL1 qi(t)Ni, и N(t) = N пр и г = 1, 2,..., k - 1,(39) N,(t) = 0 приг = k + 1,...,п,(40) к—1 Nk(t) = [Q — £ qi(tWi\/qk(t);(41) г=1 (3) множество значений t, относящихся к одному целому числу k, объединяются в полуинтервалы (тк—1,Тк]• При условии q^Ni > Q число таких полуинтервалов на всем рассматриваемом периоде равно п. Доказательство. Далее мы будем придерживаться условия, сформулированного в пункте (3) теоремы 1. Положим ф1(0) < ^2(0) <...<ф„(0). (42) Ниже, в утверждении 6, мы показываем тот же порядок функций фД^, т.е. для любого t Е [0, Т] выполнены строгие неравенства ф1(t) < ф2(t) < ... < ^„(t). Максимизация гамильтониана (27) сводится к минимизации функции „ min ^^i(t)qj(t)Ni. (43) NeG(q(t)) г=1 Сделаем замену переменных: n = qN; n = qN. В результате максимизация гамильтониана (27) свелась к следующей задаче линейного программирования: „ ^ ф-іЖ ^ min(44) г=1 при условиях „ ^Пг =Q,(45) г=1 0 6 n 6 n.(46) При этом коэффициенты фг упорядочены в порядке строгого возрастания. С учетом (45) преобразуем линейную функцию (44). В результате получаем следующую задачу линейного программирования на максимум: „—1 У2 (ф„ - фг^Пг ^ max. (47) г=1 Заметим, что коэффициенты ф' = ф„ — фг в описании линейной функции (47) положительны и убывают с увеличением порядкового номера компоненты щ. Следующая процедура позволяет найти такой оптимальный вектор n, который доставляет максимум линейной функции (47) и соответственно минимум линейной функции (44). Сначала на первом шаге выбираем n1. Если n1 > Q, то n1 = Q и щ = 0, г = 2, п. В этом случае мы определили все оптимальные значения вектора n. Если n1 < Q, то n1 = n1 и делаем замену Q = Q — u1. Далее переходим ко второй компоненте n2 и повторяем процедуру первого шага, но уже с измененным значением Q. На втором шаге измененное значение Q снова, подвергается изменению. Если мы остановились на к-м шаге, то йі = йі, г = 1,к — 1, йк = Q, йі = 0, г = к + 1,п. Если мы прошли все шаги от одного до п — 1, то йі = й, г = 1, п — 1, йп= Q. Из приведенного выше доказательства можно утверждать, что для любой к-й компоненты вектора управлений справедливо следующее: 1) если йк = йк, тoNk(t) = Nk 2) если йк = 0, то Nk(t) = 0; 3) если йк G (0,й), то Nk(t) G (0, N). Рассмотрим в динамике поведение оптимальной траектории на отрезке [0,Т]. Пусть в начальный момент q0NI > Q, тогда Ni(0) G (0,Ni), Ni(0) = 0 пр и г = 2,п. В связи с убыванием фазовой переменной qi (t) существует такой момент ті, что 1) на полуинтервале t G [0,ті) выполнены соотношения N1(t) G (0,Ni) и Ni(t) = 0 при г = 2, п; 2) УДтД = NV1 и ІЧі(т1) = 0 пр и г = 2, п. Из системы «сопряженных» уравнений (28) с учетом (29), (25), (26) при t G [0,тД получаем 7ДД = 5i (t) = 0; 3(t) = ^(t) = 3i = const; ^ДД = const пр и г = 1,п. При этом соотношения порядка, установленного среди компонент вектор-функции y(t) по их значениям в момент t = 0, не изменяются на отрезке [0,тД Далее существует такой момент т"2, что 1) на интервале (ті, т2) выполнены соотношения Ni(t) = N1, N2(t) G (0, N2) и Ni(t) = 0 при г = 3, п; 2) МД2) = Ni, ^Д2) = N2 и ТҮі(т2) = 0 пр и г = 3^. Из системы «сопряженных» уравнений (28) с учетом (29), (25), (26) при t G (ті,т2) получаем 72(t) = 52(t) = 0; 3(t) = y2(t) = 32 = const; ^ДД = const при г = 2,п; функция ^i(t) убывает на интервале (ті,72). Последнее вытекает из неравенства 31 = ^ДтД <32 = ^(тД. На отрезке [0,ті] функция д2(t) — ^i(t) постоянна, а на отрезке [ті,т2] эта функция строго возрастает. Соотношения порядка, установленные между компонентами вектор-функции ^(t) по их значениям в момент t = 0, сохраняются на отрезке [0,т2] Таким образом, отрезок [0, Т] разбивается на п отрезков [0, тД [ті, т2],..., [тп-1, тД. Здесь т„ = Т. В конце каждого к-х отрезка выполняется равенство к У^qk(тк)Nk = Q, к = 1,п. і=і Утверждение 6. Пусть t G (0,ті), к = 1, тогда 3(t) = ^i(t) = У1(0) = 3і; О Ni(t) = _ ^ и Ni(t) = 0 пр и г = 2,п; ^i(t) = ^i(0) = 3iПРи г = 2, п. Все функции ^i(t) постоянны на отрезке [0,ті]. На всем отрезке выполняются строгие неравенства ^1(t) < y2(t) < ... < yn(t). Пусть t G (т1,т2), к = 2. тогда 3(t) = ^2(t) = ^2(0) = 32 > 3i; VYi(t) = TYi, VY2(t) = Q- qi(t)N1 и VYi(t) = 0 пр иг = 3,^; 92(t) ^i(t) =^2(ті) — [^2(ті) — ^і(ті)] exp[«1 lV1(t — ті)] = ^2(0) + [^1(0) — ^2(0)] exp[a0TVi(t — ті)] = = 32 - [32 — 3і)] exp[cүІN1(t — ті)], pt (t) = pt (0) = 3i при г = 3, п. Функция p1(t) строго убывает на отрезке [ті,т2] остальные функции pt(t), г = 2,п, постоянны. На всем отрезке выполняются строгие неравенства p^t) < p2(t)< ... < pn(t). Пусть t € (тk-1,Tk), к = 3, п, тогда: 3(t) = pk(t) = pk(0) = 3к > 3к-і; Nt(t) = N при г = 1, к — 1; У ^ — ^i=k 1 9i(t)VVi n • 7—у— Nk (t) =---------—------- и Nt(t) = 0 пр и г = к + 1, п; qk(t) pt(t) = Pk(тk-i) — [pk(тк-1) — Pi(тk-1)] exp[a°Ni(t — тк-і)] = = pk(0) — [pk(0) — pi(тk-1)] exp[Q0Ni(t — Tk-1)] = = 3k — [3k — Pi(тk-1)] exp[a0Nt(t — Tk-1)] пр и г = 1,к — 1, (48) pt(t) = pt (0) = 3i при г = к + 1, п. Функции pt(t), г = 1, к — 1, строго убывают на отрезке [тk-1,Tk], остальные функции pt(t), г = к,п, постоянны. На всем отрезке выполняются строгие неравенства P1(t) < p2(t) < ... < pn(t). Доказательство. Воспользовавшись соотношениями (28), (23), (24), (25), (26), (38) и учитывая непрерывность вектор-функции p(t), выписываем формулы для вычисления переменных 3(t),N(t),p(t) на каждом из п отрезков. Строгие неравенства p1(t) < p2(t) < ... < pn(t) доказываются на каждом временном отрезке напрямую непосредственно сравнением. При этом учитываются ранее установленные порядки pi(0) < p2(0) < ... < p„(0). Конец доказательства утверждения Динамика поведения оптимальных управлений N1(t), N2(t), N3(1), функций pi(t), p2(t), p3(t) и множителя Лагранжа 3(t), полученные при решении задачи 1а размерности п = 3, схематично изображены на рис. 1. Опишем алгоритм определения непрерывной вектор-функции p(t). Сначала, воспользовавшись теоремой 1, найдем ті,т2,... ,тп = T, qt(T), г = 1,п. Далее, используя формулу (33), вычисляем точные значения вектора p(T), компоненты которого, согласно утверждению 5, расположены в возрастающем порядке. Дальнейший алгоритм поиска основывается на результатах, сформулированных в утверждении 6. Затем будем последовательно рассматривать отрезки, начиная с [тп-і,Т] и кончая [0,тД Нам известны множитель Лагранжа 3(t) = 3п на п-м интервале (тп-і,Т), функция pn(t) = pn(0) = pn(T) = 3n на отрезке [0,Т] и величины pt(T), г = 1,п, при которых выполняются строгие неравенства Pi(T) < p2(T) < ... < pn(T). Все остальные компоненты вектор-функции p(t) на п-м от резке [тn-1,T ] вычисляются по формуле pt(t) = pn(T) — [p„(T) — pt(T)] exp[—a0Ni(T — t)], г = 1,п — 1. (49) Очевидно, на п-м от резке [тn-1,T ] выполняется неравенство pt(t) < pn(t) = pn(T) = pn(0) = 3n, г = 1,п — 1. Таким образом, мы находим все значения pi(тn-1), г = 1,п, и т. д. Переходим к последовательному исследованию функций на к-м отрезке [тk-1,Tk], к = 1,п — 1. Нам известны все значения pi(тk), г = 1,п. Также нам известны функции pt(t) = pi(тk) = 3t, г = к + 1,п, на от резке [тk-1,Tk ]. Определяем множитель Лагранжа 3(t) = 3k на к-м интервале (тk-1,Tk) и функцию pk(t) = pk(0) = pk(тk) = 3k Рис. 1. Динамика поведения оптимальных управлений N1(6), N2(t), N3(1), функций 91(6), tp2(t), 93 (t) и множителя Лагранжа /3(t) в решении задач и 1а размерности п = 3 на отрезке [0, Тк ]. Все остальные компоненты вектор-функции y(t) на к-м от резке [тк—1,Тк ] вычисляются по формуле Vt(t) = Vk(тк) — [vk(Тк) -9і(тк)]exp[-a0Ni(Tk — t)], г = 1,к — 1. (50) Таким образом, для каждого значения к = 1,п — 1 мы находим все 9і(тк—і), г = 1,п. В том числе на первом отрезке мы определяем все величины 9t(0), г = 1,п. Значит, мы на отрезке [0, Т] построили однозначную вектор-функцию v(t), удовлетворяющую условиям трансверсальности (33). Более того, эта функция единственная. Действительно, любой начальный порядок компонент вектор-функции отличный от (42), не приводит к максимизации гамильтониана (27), что противоречит существованию оптимальной траектории. Следовательно, мы нашли единственную «сопряженную» функцию удовлетворяющую необходимым условиям оптимальности в форме Эрроу. Теорема 1 доказана.
5. Заключение При разработке группы газовых месторождений первостепенной задачей в каждый момент времени является выполнение текущего плана по добыче газа. В начальный период его можно выполнить разными способами. Однако наступает момент, когда не хватает добывающих мощностей для его выполнения. В этой связи интересно определить все возможные значения, которые принимает длина «полки» группы газовых месторождений. Для этого необходимо решить задачу оптимального управления на максимум и на минимум. В настоящей статье дается решение одной задачи на максимум. Все месторождения в группе сортируются по величине показателя a^Nt от наименьшего значения к наибольшему. Плановый период разбивается на п частей, равных числу месторождений в группе. В начале каждой части в разработку вводится следующее по порядку месторождение. Все ранее введенные месторождения продолжают работать до конца планового периода на предельных своих мощностях, но этого недостаточно, чтобы обеспечить выполнение текущего плана по совокупной добыче газа. По этой причине в разработку вводится новое месторождение. В конце данной части планового периода в разработку вводятся все скважины на новом месторождении. В конце планового периода в разработке задействованы все скважины всех месторождений. Возможная дальнейшая разработка приведет только к невыполнению плана по совокупной добыче газа.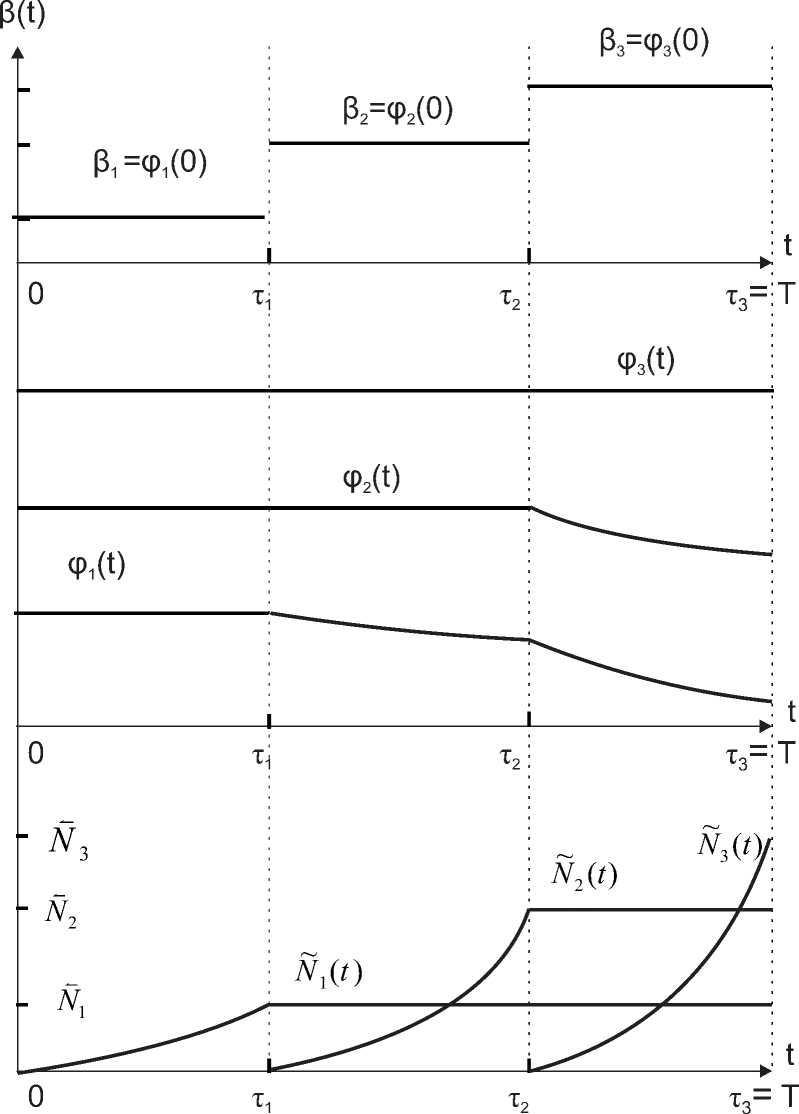
Список литературы Поиск в модели газовых месторождений максимальной длины их общей "полки"
- Вяхирев Р.И., Коротаев Ю.П., Кабанов Н.И. Теория и опыт добычи газа. Москва: Недра, 1998.
- Эрроу К. Применение теории управления к экономическому росту//Матем. экономика. Москва: Мир, 1974. C. 7-45.
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. Москва: Наука, 1976.
- Skiba A.K. Optimal Growth with a Convex-concave Production Function//Econometrica. 1978. V. 3(46). P. 527-539.
- Тер-Крикоров A.M. Оптимальное управление и математическая экономика. Москва: Наука, 1977.
- Асеев С.М., Кряжимский А.В. Принцип максимума Понтрягина и задачи оптимального экономического роста//Труды МИАН. М: Наука/Интерпериодика MAIK. 2007. Т. 257. С. 3-271.
- Balder E. Existence Result for Optimal Economic Growth Problems//Journal of Mathematical Analysis and Applications. 1983. V. 95. P. 195-213.
- Маргулов Р.Д., Хачатуров В.Р., Федосеев А.В. Cистемный анализ в перспективном планировании добычи газа. Москва: Недра, 1992.
- Хачатуров В.Р., Соломатин А.Н., Злотов А.В. . Планирование и проектирование освоения нефтегазодобывающих регионов и месторождений: Математические модели, методы, применение/Под ред. В.Р. Хачатурова. Москва: УРСС: ЛЕНАНД, 2015.
- Ли Э.Б., Маркус Л. Основы теории оптимального управления. Москва: Наука, 1972.
- Моисеев Н.Н. Элементы теории оптимальных систем. Москва: Наука, 1975.


