Поиск впадин в замкнутом невыпуклом контуре

Как известно, структурные методы распознавания объектов основаны на поиске элементарных составляющих объекта и анализе их взаимного расположения [3]. Однако поиск этих элементарных составляющих представляет трудности, отчасти из-за сложности формализации, отчасти из-за их многообразия. Видимо, для того, чтобы создать методы распознавания, сравнимые по надежности с человеком, необходимо формализовать все понятия, свойства и определения Евклидовой геометрии, поскольку все это когда-то заметил и выделил человек.

Далее речь пойдет о структурных элементах, которым до сих пор уделялось мало внимания. Большинство объектов реального мира представляет собой невыпуклые многогранники, проекции контура которых на плоскость обычно являются невыпуклыми многоугольниками (рис. 1).

Рис. 1. Примеры невыпуклых многогранников реального мира. а) Автомобиль ВАЗ-2110.

б) Истребитель-бомбардировщик Су-30

В данной статье описывается алгоритм поиска впадин в замкнутом невыпуклом контуре, представленном восьмисвязной цепью переходов (код Фримена) [4].

1. Основная идея

Чтобы проиллюстрировать принцип поиска впадин, приведем несколько примеров, переходя от простых к более сложным.

Прежде всего, для каждого невыпуклого многоугольника можно построить минимальный по площади объемлющий его выпуклый многоугольник и найти, таким образом, впадины (рис. 2а). Однако этим способом далеко не всегда удается найти все впадины, которые выделил бы человек (рис. 2б).

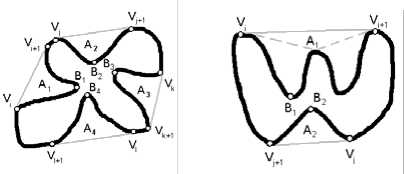
Рис. 2. Поиск впадин с помощью построения минимального объемлющего многоугольника. а) Пример удачного поиска. б) Впадину A 1 хотелось бы разделить на две

Введем предварительно несколько определений и обозначений.

Вершины выпуклого многоугольника для данного контура будем обозначать как множество V = { V i } iV0 1 , множество впадин - A = { A i } A ₀ 1 . Договоримся, что впадина (A_i ) ограничивается с одной стороны контуром объекта, а с другой – отрезком прямой, концы которого принадлежат контуру. Концы отрезка называются краями впадины (обозначаются E^'_i и E^'_i^' ). Весь замкнутый контур будем обозначать Г , а часть его, принадлежащую впадине A i - Г A . Ограничивающий отрезок впадины E i E " не пересекает Г _А нигде, кроме своих концов (условие несамопересечения границы впадины). Будем считать, что концами ограничивающего отрезка могут являться не любые, а только некоторые особенные точки контура, при этом впадина должна иметь максимально возможные размеры и иметь как можно более близкую к выпуклому многоугольнику форму.

Дадим определение максимального отклонения множества точек от отрезка. Это не то же самое, что максимальное отклонение от прямой, и зависит от трех величин – максимального прямоугольного и двух максимальных тупоугольных отклонений от отрезка.

Максимальным прямоугольным отклонением множества S от отрезка AB называется максимум расстояния от точек множества до прямой, проходящей через отрезок:

сmax (S,AB) = max{с 1 (s,AB)}.(1)

Областью тупых углов Ф _в для конца B отрезка AB будем называть множество таких точек T, для которых угол TBA – тупой:

Ц^в = {T:2 < ZTBA < р}.(2)

Тупоугольным отклонением точки M от конца B отрезка AB будем называть следующую величину:

с((M,BA) =

с(M,B), если M е Ц ^ ^в

• 0, если M g Ц ^ ³

Следует обратить внимание, что в формуле конец отрезка, относительно которого считается отклонение, записывается первым.

Максимальным тупоугольным отклонением множества точек S от конца A отрезка AB называется максимум из тупоугольных отклонений точек S от конца отрезка A:

с max ( ^S,AB ) = max { с ⁽( ^s,AB ) } . ses

Максимальным отклонением множества S от отрезка AB называется максимум из прямоугольного отклонения и тупоугольных отклонений от обоих его концов (рис. 3):

с max ( S,V i V j ) =

= ^ma x { с max ( ^S,AB ) ,с L ( ^S,AB ) , с max ( S,BA ) } .

Глубиной впадины A_i будем называть максимальное отклонение фрагмента контура впадины Г _А от ограничивающего ее отрезка E i E i :

d i = с max ( r A i ,E i E " ) ,

а точку контура, в которой достигается этот максимум, назовем донной точкой и будем обозначать Bi .

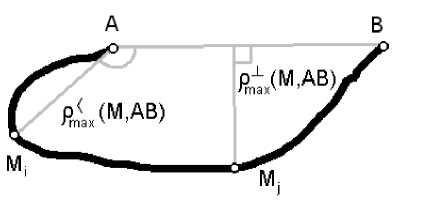
Рис. 3. Максимальное прямоугольное и тупоугольное отклонения фрагмента контура от отрезка

Вернемся к примерам впадин. На рис. 2 б с помощью максимального объемлющего выпуклого многоугольника было найдено разделение контура на впадины, которое не совсем соответствует человеческому представлению о том, как оно должно выглядеть. Впадину A 1 хотелось бы поделить на две, как это сделать? Наиболее очевидным представляется использовать как точку разделения вершину самой заметной выпуклости внутри впадины. Рассмотрим впадину A₁ как невыпуклый контур, состоящий из фрагмента контура Г _А 1 и ограничивающего впадину отрезка V i V i+1 . Построим для данного невыпуклого контура выпуклый многоугольник, точнее, выпуклую ломаную (поскольку одна сторона многоугольника уже известна – это ограничивающий отрезок) (рис. 4 а ).

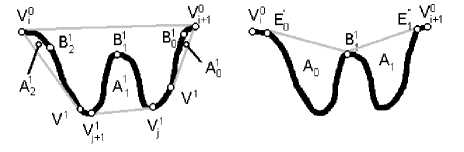
Рис. 4. Разделение впадины A ₁ ⁰ рис. 2б. а) Поиск впадин первого порядка.

б) Найденные впадины A ₀ и A ₁ с краями, удовлетворяющими условию несамопересечения

Выпуклой ломаной будем называть ломаную, которая достраивается до выпуклого многоугольника соединением крайних концов. Выпуклая ломаная является минимальной для данного фрагмента контура, если получаемый из нее выпуклый многоугольник имеет наименьшую площадь. Выпуклые ломаные можно строить с двух сторон фрагмента, при достраивании до многоугольника они не обязательно должны содержать фрагмент целиком (рис. 5).

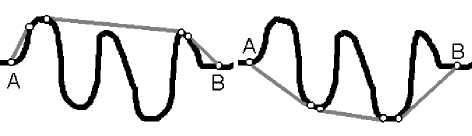
Рис. 5. Выпуклые ломаные для фрагмента контура AB можно построить с двух сторон

Границу выпуклого многоугольника для всего контура будем обозначать Q , а границу выпуклой ломаной для впадины A, ограниченной отрезком E'E" - Q A или Q _EE- .

Прежде чем рассматривать, что у нас получилось после построения выпуклой ломаной для впадины, введем понятие порядка для многоугольников и ломаных, их вершин, впадин и донных точек. Нулевой порядок присваивается выпуклому многоугольнику, построенному для исходного замкнутого контура, а также его вершинам, впадинам и их донным точкам. Первый порядок присваивается выпуклым ломаным, построенным для впадин нулевого порядка, а также их вершинам, впадинам и их донным точкам. И так далее, аналогично определяются более высокие порядки. Порядок объекта будем обозначать верхним индексом.

Таким образом, выпуклости внутри впадины нулевого порядка превращаются во впадины первого порядка. На рис. 4 а у нас получилось три впадины и три донные точки первого порядка, причем только одна из впадин (A¹₁ ) имеет заметную глубину. Донную точку этой впадины B¹₁ можно использовать для разделения исходной впадины A₁⁰ на две, а донные точки B¹₀ и B¹₂ можно проигнорировать. Тем не менее, может потребоваться коррекция краев впадины, чтобы выполнялось условие несамопересечения (рис. 4 б ).

Покажем, как производится коррекция несамо-пересечения. Пусть есть фрагмент контура, между крайними точками (V i и V j ) которого есть впадина, для которой известно положение донной точки B (рис. 6). Построим минимальную выпуклую ломаную, ограничивающую фрагмент с внешней стороны. Находим тот отрезок ломаной (E'E"), который ограничивает впадину, содержащую заданную точку B. Концы этого отрезка и будут скорректированными краями впадины.

Рассмотрим более сложную впадину нулевого порядка, внутри которой несколько впадин первого порядка (рис. 7). Очевидно, их донные точки можно использовать для разделения впадины нулевого порядка. Таким образом, впадина нулевого порядка делится на впадины, число которых не превышает число ее впадин первого порядка плюс одна.

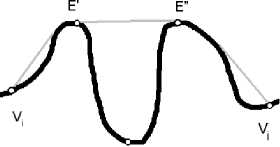
Рис. 6. Коррекция несамопересечения. B – заданная донная точка, V i ,V j – первое приближение краев впадины, E', E" – края впадины после коррекции

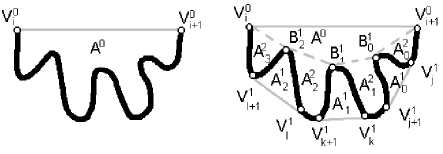
Рис. 7. Разделение впадины нулевого уровня с помощью трех донных точек первого уровня.

Граничные отрезки конечных впадин обозначены пунктиром

Однако что будет, если впадина первого порядка имеет более сложный вид и в ней самой можно выделить впадины (рис. 8 а , 8 б )?

Рис. 8. Разделение впадины нулевого порядка (а) с помощью сложной впадины первого порядка (б).

Предварительно впадина первого порядка делится с помощью донных точек впадин второго порядка (в).

Впадина нулевого порядка делится донными точками получившихся впадин первого порядка (г)

Разделим данную впадину на две. Для этого построим для нее минимальную выпуклую ломаную и найдем впадины второго порядка (рис. 8 в ). Как и в случае на рис. 4, используем донную точку впадины A₁² для разделения. Донные точки двух получив-

шихся впадин первого порядка можно использовать для разделения исходной впадины нулевого порядка на три (рис. 8 г ).

Таким образом, основная идея алгоритма поиска впадин следующая. После построения для невыпуклого контура минимального выпуклого многоугольника находится некоторое число впадин нулевого порядка. Для каждой из этих впадин выясняется, не является ли она невыпуклым контуром с впадинами первого порядка. Для найденных впадин первого порядка, в свою очередь, проверяется, не являются ли они сами невыпуклыми контурами с впадинами второго порядка, и т.д., рекурсивно анализируем впадины все более высоких порядков, пока очередная впадина не окажется выпуклым и, следовательно, неделимым контуром. Затем происходит обратный процесс – с помощью донных точек впадин глубоких порядков пытаемся разделить впадины предыдущих порядков, пока не вернемся на нулевой уровень.

3.    Поиск минимальных выпуклых многоугольников и ломаных

По определению, выпуклым называется такой многоугольник, который целиком лежит в одной полуплоскости относительно прямой, проведенной через любую из его сторон. Воспользуемся этим определением при построении выпуклого многоугольника для данного невыпуклого многоугольника.

Граничной прямой многоугольника будем называть такую прямую, которая проходит минимум через две его вершины так, что весь многоугольник лежит по одну сторону от прямой. Часть прямой, лежащая между этими двумя вершинами, называется граничным отрезком. В каждом невыпуклом многоугольнике есть выпуклые (меньше π ) и вогнутые (больше π ) углы. Очевидно, что граничная прямая должна проходить через вершины, углы в которых выпуклые (рис. 9).

Рис. 9. Невыпуклый многоугольник Q и одна из его граничных прямых a

Рассмотрим контур, представляемый восьмисвязной цепью, как невыпуклый многоугольник. Каждая точка цепи является либо выпуклой или вогнутой вершиной многоугольника, либо лежит на прямой, соединяющей вершины (в данном случае прямыми считаются только строго горизонтальные, вертикальные и диагональные участки). Точки цепи будем называть выпуклыми (множество P={P i }), вогнутыми (множество C={C_i}) или прямыми, в зависимости от того, соответствуют ли они какому-то углу или лежат на прямом участке (рис. 10).

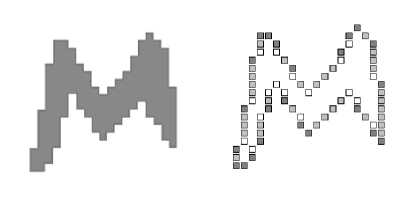
Рис. 10. а) Исходный растровый объект. б) Контур объекта, всего 74 точки, из них 23 (31%) – выпуклые (темно серые), 18 (24%) – вогнутые (белые), остальные 33 (45%) – прямые (светло серые)

Переберем все пары выпуклых точек и найдем такие из пар, через которые можно провести граничную прямую. При этом для каждой пары составляем уравнение прямой вида

0:	max ( Px ) , i=0,P -1	р 4:	max i=0, P -1	( P ix	+ P iy
р 2:	max ( Py ) , i=0,P -1	3р 4:	max i=0, P -1	( P iy	- P ix
р:	min ( ^x ) , i=0,|P|-1	5р 4:	min i=0,P|-1	( P iy	+ Px
3р 2:	min ( P y ) , i=0,P -1	7р 4:	min i=0,|P|-1	( P iy	- P ix

где Pix, Piy – координаты выпуклой точки Pi .

Для того, чтобы при поиске граничных прямых сразу отсечь много заведомо неподходящих пар, достаточно подставить в уравнение прямой одну из экстремальных выпуклых точек, а именно ту, направление экстремума которой наиболее близко к нормали прямой, направленной в отрицательную полуплоскость. Если невязка этого экстремума отрицательная, значит прямая не является граничной (рис. 12 б ).

ax + by + c = 0

и проверяем, все ли выпуклые точки лежат по одну сторону от прямой. Это выполняется, если при подстановке в уравнение всех точек P i невязки ax i +by i +c получаются одного знака либо равными нулю. Пусть уравнение нормализованное, т.е. a²+b²=1, тогда модули невязок равны расстоянию от точек до прямой. Если смотреть по ходу направляющего вектора (-b,a), то полуплоскость неотрицательных невязок лежит справа от прямой. Всегда можно построить уравнение так, что если прямая является граничной, то невязки всех точек контура неотрицательные (рис. 11): ax + by + c >  0.

положительные невязки

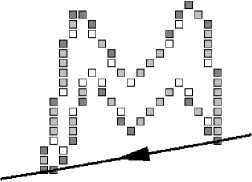
отрицательные невязки

Рис. 11. Деление плоскости граничной прямой на область положительных и отрицательных невязок.

Стрелкой показан направляющий вектор прямой

При вычислении на ЭВМ из-за ошибок округления реальные невязки могут получиться отрицательными даже в тех двух точках, через которые проводилась прямая, таким образом, граничные прямые вообще могут не найтись. Поэтому невязки сравниваются не с нулем, а с близкой к нулю отрицательной константой:

ax + by + c > -е , 0 < е ® 0, идеально использовалось s = 0.0001.

То, что при поиске граничных прямых проверяются не все пары, а только пары выпуклых точек, дает существенную экономию вычислений. Однако можно добавить дополнительную проверку, отсекающую заведомо плохие пары. Найдем среди выпуклых точек экстремумы по восьми направлениям (рис. 12 а ):

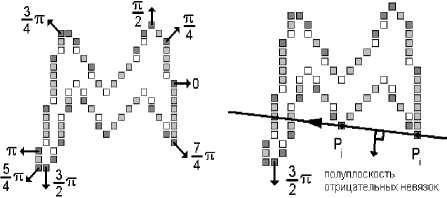
Рис. 12. а) Экстремальные выпуклые точки контура по восьми направлениям. б) Экстремальный одноточечный тест для прямой. P i P j – экстремальная точка с наиболее близким к нормали прямой направлением лежит в отрицательной полуплоскости

Первый граничный отрезок ищется последовательным перебором пар выпуклых точек. Как только он найден, каждый следующий граничный отрезок строится с использованием одной из вершин предыдущего, и так до тех пор, пока не будут найдены все граничные отрезки. Для замкнутого контура получается выпуклый многоугольник, для фрагмента – выпуклая ломаная (рис. 13).

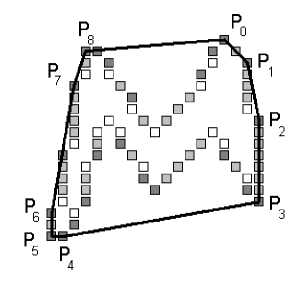
Рис. 13. Найденный минимальный выпуклый многоугольник

4.    Поиск донных точек во впадинах

Теперь перейдем к поиску донных точек внутри впадин. Наиболее простой способ – перебрать все точки внутри впадин, вычисляя для каждой прямо- угольное и тупоугольное отклонения, однако попробуем выяснить, в каких точках поиск максимума отклонения является заведомо бесперспективным. Сначала докажем несколько вспомогательных утверждений. Модулем отрезка будем обозначать его длину.

Утверждение 1 . В части плоскости, ограниченной произвольным треугольником ABC? наиболее удаленной от точки A точкой является одна из двух других вершин B и C, но не внутренняя точка треугольника и не точка, лежащая на одной из сторон.

Доказательство.

Докажем сначала, что любая внутренняя точка P ближе к A, чем одна из двух других вершин (рис. 14 а ).

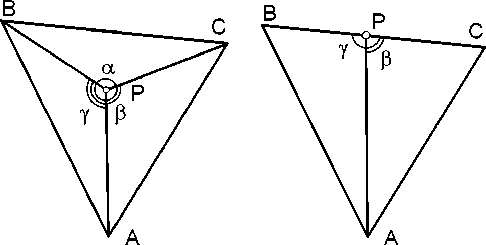
Рис. 14. В любом треугольнике для любой его вершины наиболее удаленной точкой является одна из двух других его вершин (иллюстрации к доказательству)

С помощью точки P и вершин A, B, C можно построить три треугольника. Сумма углов α , β , γ равна 2 π , каждый из этих углов меньше π , поскольку принадлежит вершине треугольника. Докажем, что хотя бы один из углов β , γ обязательно неострый, т.е. прямой или тупой. В треугольнике самая длинная сторона противолежит самому большому углу, а неострый угол в треугольнике может быть только один. Это будет означать, что AP короче, чем одна из сторон AB или AC.

α<π ⇒ π–α>0

β+γ = 2π–α = π+π–α > π ⇒ β+γ>π

Если β неострый, то |AP|<|AC|, что и требовалось, но предположим противное.

Если β< р2 , то р2 –β>0, тогда γ > π–β = р2 + р2 –β > р2 ⇒ γ> р2 ⇒

|AP|<|AB|. Аналогично, если γ < ^р ₂ , то β > ^р ₂ ⇒ |AP|

Докажем теперь, что наиболее удаленная от A точка не может лежать на одной из сторон треугольника. То, что она не лежит на AB или AC, очевидно. Докажем что она не лежит и на BC (рис. 14 б ).

β + γ = π . Докажем, что хотя бы один из углов β , γ неострый. Если β неострый, то AP короче, чем AC, что и требовалось, но предположим противное.

Если β < ^р ₂ , то γ = π – β = ^р ₂ + ^р ₂ – β >  ^р ₂ ⇒ γ > ^р ₂ ⇒ |AP|<|AB|. Аналогично, если γ < ^р ₂ , то β > ^р ₂ ⇒ |AP|<|AC|.

Утверждение 2 . В любой области Q, ограниченной выпуклым многоугольником, наиболее удаленной от произвольной точки A ∈ Q является одна из вершин этого многоугольника.

Доказательство.

Поскольку многоугольник выпуклый, точку A можно соединить со всеми вершинами многоугольника отрезками, которые целиком лежат внутри многоугольника, образующиеся при этом треугольники так же лежат внутри многоугольника и покрывают его целиком (рис. 15). Поиск наиболее удаленной от A точки сводится к поиску наиболее удаленной точки в каждом треугольнике, а затем к выбору максимума по всем треугольникам. По доказанному утверждению 1 в каждом треугольнике наиболее удаленной от A является одна из двух других его вершин, которая в то же время является вершиной многоугольника, что и требовалось доказать.

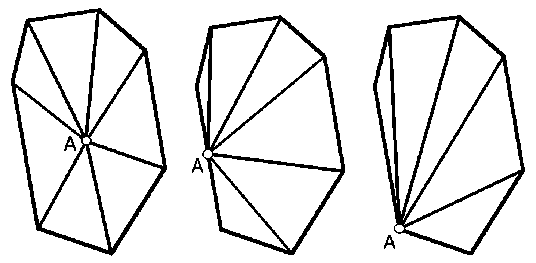
Рис. 15. Где бы ни была взята точка A, принадлежащая области, ограниченной выпуклым многоугольником – внутри, на стороне, в одной из вершин, эту область всегда можно разделить на треугольники, одной из вершин которых будет A

Утверждение 3 . В любой области Q, ограниченной выпуклым многоугольником, максимум расстояния до произвольной прямой AB достигается в одной из вершин этого многоугольника или в целой стороне, которая параллельна прямой AB (доказательство пропущено).

Из двух последних утверждений следует, что донную точку впадины по формуле (6) нужно искать среди вершин минимальной ограничивающей впадину выпуклой ломаной. Докажем это. Пусть есть впадина, ограниченная отрезком AB, построим для нее выпуклую ломаную Ω _AB со множеством вершин V={V i }, которая вместе с отрезком AB ограничивает выпуклую область U (рис. 16 а ). Все точки, образующие контур впадины Γ AB и не лежащие на Ω _AB, являются внутренними точками U, из утверждения 3 следует, что расстояния до ограничивающей прямой в них не могут быть больше, чем расстояние от прямой до одной из вершин V.

Как ведет себя тупоугольное отклонение? Выделим подмножество точек W⊆U, которые образуют тупой угол с вершиной B ограничивающего отрезка: W⊂ΦB (напомним, что ΦB – область тупых углов для конца B отрезка AB, определяемая формулой (2) (рис. 16б). W так же ограничивается выпуклым многоугольником ΩW, в нем есть вершина P, лежащая на перпендикуляре к отрезку AB, эта вершина мо- жет совпадать с одной из вершин ΩAB или делить ее сторону, отрезок BP не принадлежит ΦB, поскольку лежит на перпендикуляре к точке B.

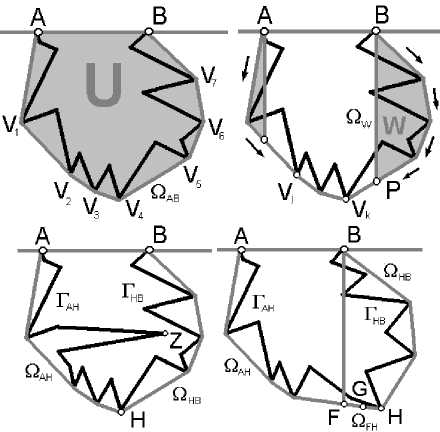
Рис. 16. а) Для впадины, ограниченной отрезком AB, построен минимальный объемлющий выпуклый многоугольник U. б) Серым обозначены области поиска максимального тупоугольного отклонения от отрезка, стрелками показано направление обхода вершин U для обоих концов отрезка AB.

• в) Точка максимального прямоугольного отклонения H делит фрагмент контура Γ AB и соответствующую ему выпуклую ломаную Ω AB на две части, в части Γ AH не может достигаться максимум тупоугольного отклонения от точки B, а в части Γ AH – максимум тупоугольного отклонения от точки A. г) Даже если часть ломаной Ω AH принадлежит области Φ B , в ней и соответствующем ей фрагменте контура Γ _AH не может достигаться максимум тупоугольного отклонения от точки B

Согласно утверждению 2, наиболее удаленной от точки B внутри W является одна из вершин ΩW, если это P, то с〈max(ЩW,BA)≤с⊥(P,AB), с⊥(P,AB)≤с⊥max(ЩAB,AB)=с⊥max(V,AB).

То есть, если P не совпадает ни с одной из вершин Ω AB , нет необходимости искать ее специально, поскольку прямоугольное отклонение в ней не превысит максимальное прямоугольное отклонение ломаной Ω AB от отрезка AB.

Таким образом, если для впадины известен выпуклый многоугольник, то для поиска донной точки по формуле (6) нужно проверить лишь значения отклонений в его вершинах. Кроме того, при поиске тупоугольных отклонений от каждого конца отрезка нет необходимости проверять все вершины многоугольника. Для каждого конца нужно начать проверку с ближайших по циклу вершин ломаной ΩAB, и как только окажется, что очередная проверяемая вершина не составляет с отрезком тупой угол, проверку следует прекратить, поскольку выпуклая ломаная уже не возвращается в область тупых углов данного конца отрезка (рис. 16б, направления обхода для каждого конца отрезка при поиске максимального тупоугольного отклонения показаны стрелками).

Когда найдены максимальные тупоугольные отклонения от обоих концов и первые выходящие из областей тупых углов вершины ломаной Ω AB (V j и V k для концов A и B соответственно), то можно сэкономить вычисления при поиске максимального прямоугольного отклонения. В области тупых углов для любой вершины Ω W прямоугольное отклонение меньше тупоугольного, поэтому там прямоугольное отклонение вычислять не следует, необходимо проверить лишь вершины многоугольника от V j до V_k включительно.

Если же для впадины неизвестен выпуклый многоугольник, то поиск максимального отклонения не следует проводить в таких точках ее контура, которые не могут являться вершинами выпуклого многоугольника, а именно, в тех, которые для контура впадины являются вогнутыми или прямыми. Это дает существенную экономию вычислений, однако число операций можно еще уменьшить.

Пусть найдена точка максимального прямоугольного отклонения H, по утверждению 3 она лежит на выпуклой ломаной Ω AB фрагмента контура впадины Γ AB и делит его на участки Γ AH и Γ HB (рис. 16 в - г ). Хотя ломаная Ω AB и считается неизвестной, будем помнить, что максимум прямоугольного отклонения достигается в одной из ее точек или в целом отрезке, параллельном AB, и будем использовать свойства выпуклой ломаной. Обратим внимание, что часть ломаной Ω _AH не может содержать точек из фрагмента контура Γ HB , поскольку это означало бы самопересечение контура Γ AB . Аналогично, часть ломаной Ω _HB не может содержать точек из фрагмента контура Γ AH .

Докажем, что максимум тупоугольного отклонения для концов отрезка A и B не нужно искать во фрагменте контура Γ _HB и Γ _AH соответственно. Если точка H лежит вне Φ _A и Φ _B (рис. 16 в ), то это очевидно: при вычисления тупоугольного отклонения от точки B часть ломаной Ω _AH полностью лежит вне Φ _B. Даже если часть точек фрагмента Γ _AH и попадает в Φ _B (например, точка Z ), то, поскольку эти точки не могут лежать на выпуклой ломаной, максимум тупоугольного отклонения в них достигаться не может. Аналогично для тупоугольного отклонения от точки A внутри фрагмента Γ HB .

Допустим, что точка H лежит в одной из областей тупых углов, например в Φ В (рис. 16 г ). Рассмотрим Ω FB – фрагмент выпуклой ломаной, лежащий в Φ В . Точка H делит Ω FB на две части – Ω HB и Ω _FH ⊂ Ω _AH. Рассмотрим произвольную точку G ∈ Ω _FH (G ≠ H). Поскольку H – точка максимального прямоугольного отклонения, G лежит не дальше от прямой AB, чем точка H:

p^± (G,AB) < p^± (H,AB).

Кроме того, G ближе, чем H, к перпендикулярной AB прямой BF:

p^± (G,BF) <  p^± (H,BF).

Расстояние от G до B меньше расстояния от H до B:

p ²(G,B) = HG,AB)]² + [ p^± (G,BF)]²<

• < p²(H,B) = [p^±(H,AB)]² + [p^BF)]².

5.    Рекурсивный поиск впадин

Таким образом, внутри Q _FH не может находиться максимум тупоугольного отклонения от точки B, внутри Q _af тупоугольное отклонение от точки B равно нулю, следовательно, и внутри части контура впадины r _AH, ограниченного частью ломаной Q _AH, не следует проверять максимальное тупоугольное отклонение от точки B.

Таким образом, поскольку вычисление прямоугольного отклонения от прямой проще вычисления тупоугольного отклонения от конца отрезка, сначала следует найти точку максимального прямоугольного отклонения H, а затем проверить для каждой вершины максимальное тупоугольное отклонение в двух фрагментах r _AH и r _HB, причем только в выпуклых точках.

В описываемом далее алгоритме используются оба способа поиска - в одних случаях для впадины выпуклый многоугольник известен, в других - нет.

Как говорилось ранее, впадины ищутся путем деления впадин нижних порядков с помощью донных точек впадин верхних порядков. Для этого предварительно находятся все впадины, вплоть до самых высоких неделимых порядков. При этом получается иерархический буфер ломаных (рис. 17). При поиске выпуклые и вогнутые точки меняются ролями в зависимости от номера порядка: для четных порядков вершины ломаных ищутся среди выпуклых точек, а донные точки - среди вогнутых; для нечетных: вершины ломаных - среди вогнутых, а донные - среди выпуклых.

Рис. 17. Структура иерархического буфера ломаных. На рисунке каждый ограничивающий отрезок нумеруется числом индексов, равным его порядку, увеличенному на 1

Введем положение: впадина называется заметной, если она удовлетворяет некоторым требованиям, например, ее глубина не меньше некоторой минимальной константы, которая может зависеть от размера контура, или площадь, не меньше некоторой минимальной площади, которая может зависеть от площади минимального объемлющего выпуклого многоугольника, или она заметно отличается от прямой (при этом глубина не является пренебрежи- мо малой по сравнению с длиной отрезка, ограничивающего впадину. Чтобы реализовать такое условие, требуется коррекция пологих склонов, об этом будет сказано далее, или какое-нибудь другое условие.

Донные точки заметных впадин самого высокого неделимого уровня переходят на предыдущий и с их помощью делается попытка разделить впадину предпоследнего уровня, как это описывалось в пункте 2. Если это удается, то донные точки получившихся при разделении впадин переходят на предыдущий уровень. Если впадину не удалось разделить, то проверяется, является ли она сама заметной, и если да, то ее донная точка переходит на предыдущий уровень. Поскольку для всех впадин известны объемлющие их выпуклые многоугольники, в этом случае донные точки ищутся только среди вершин этих многоугольников.

Опишем процесс деления подробнее. Путь в данной впадине A есть несколько донных точек более высокого уровня B i , i=0,...,N-1; и кроме них еще две точки ограничивающего отрезка E' и E". Делим часть контура r (A) на фрагменты E'B₀, B 0 B 1 ,..., B_N- 2 B N-1 , B n-i E".

Края фрагментов являются первым приближением краев впадин. Поскольку нет гарантии, что эти края удовлетворяют условию несамопересечения, для каждого фрагмента строим выпуклую ломаную, которая ограничивает его с внешней стороны (рис. 18 а ), в этой ломаной нас интересуют лишь отрезки, ограничивающие заметные впадины.

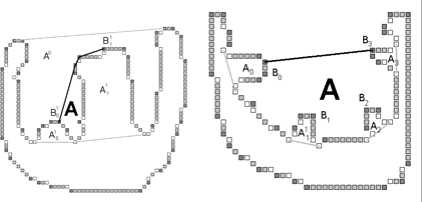
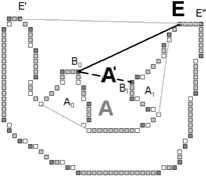
Рис. 18. Иллюстрации к алгоритму поиска впадин с помощью иерархического буфера ломаных.

а) Поиск заметной впадины (A) с помощью выпуклой ломаной между двумя донными точками B 0 и B 1 . б) Объединение фрагментов контура B 0 B 1 , B 1 B 2 и B 2 B 3 в один после того, как внутри них не было найдено заметных впадин. В результате в объединенном фрагменте найдена впадина A.

в) Коррекция края впадины на нулевом уровне. На фрагменте B₀B₁ найдена впадина А (граница обозначена пунктиром), а на фрагменте B 1 E" заметных впадин нет. После коррекции в объединенном фрагменте B 0 E" найдена впадина A' с краями B₀E

Как правило, их не больше одной либо нет совсем, но нет гарантий, что нельзя придумать такой критерий заметности впадины, при котором их может получиться больше одной. Если в критерий заметности входит глубина впадины, то в данном случае, поскольку выпуклый многоугольник неизвестен, донная точка ищется среди выпуклых точек впадины.

Может случиться, что для нескольких подряд идущих фрагментов не будет найдено ни одной заметной впадины, но их можно объединить в один и попробовать найти в нем хотя бы одну заметную (рис. 18 б ).

Бывает, что при делении впадины донными точками предыдущего уровня остаются фрагменты, в которых не удалось найти заметных впадин (в том числе после объединения). Поскольку на всех уровнях выше нулевого нас интересуют лишь донные точки впадин, а не их края, это не имеет значения на всех уровнях, кроме нулевого, когда края впадин определяются окончательно (рис. 18 в ). В связи с этим проводится следующая коррекция.

Пусть впадина нулевого уровня разделена донными точками первого уровня так, что внутри хотя бы одного из крайних фрагментов (пусть это будет B N-1 E") нет впадины. Тогда ближайшую к этому краю найденную заметную впадину (впадина A, фрагмент, содержащий ее – B i B i+1 ) можно переопределить. Для этого объединим в один фрагмент все точки между B i и E" и попробуем найти внутри него заметные впадины. Если это не удастся, то впадина A остается без изменений, иначе на ее месте возникает впадина с другими краями.

Главным недостатком алгоритма является то, что границы впадин не всегда получаются такими, какими их представляет себе человек. Иногда получаются впадины с пологими склонами, переходящими в резкие (рис. 19), и если на склоне есть точка резкого разделения пологого и крутого участка, например, разрыв первой или второй производной направления контура – угол (рис. 19 а ) или точка изменения характера кривизны (рис. 19 б ), соответственно, то границу впадины хотелось бы определить в ней. В будущем предполагается добавить к алгоритму коррекцию пологих склонов с использованием особенных точек контура (алгоритмы поиска углов описаны в [2]). В отсутствие точки разделения (рис. 19 в ) коррекция производиться не будет. Также коррекция не будет производится, если особенная точка разделяет не пологую и крутую часть склона, а крутую и еще более крутую (рис. 19 г ).

6.    Область применения алгоритма

Наиболее очевидными характеристиками впадин являются площадь, координаты геометрического центра и донной точки, ориентация нормали ограничивающего отрезка. Впадины, наряду с внутренними замкнутыми областями и углами, являются характерными структурными элементами рукописных символов (рис. 20а). С помощью анализа вза- имного расположения впадин можно классифицировать объекты.

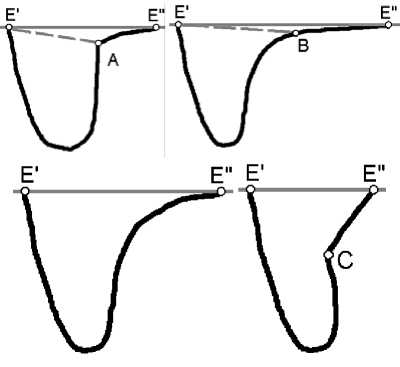
Рис. 19. а) Коррекция пологого склона впадины E'E" по угловой точке A. б) Коррекция пологого склона впадины E'E" по точке изменения характера кривизны B. в) Коррекция пологого склона не производится, поскольку на нем нет особенных точек. г) Переход крутого склона в еще более крутой; несмотря на то, что есть угловая точка C, коррекция не производится

В [1] описывается алгоритм совмещения точек на стереопарах с помощью поиска углов, впадины могут служить дополнительным структурным элементом при совмещении, поскольку поиск углов не всегда работает успешно [2], кроме того впадины можно найти даже там, где ярко выраженных углов нет.

Поиск впадин можно также использовать как альтернативу методам скелетизации, главным недостатком которой, как известно, является то, что небольшие шероховатости контура могут превращаться в длинные ветви. Соединяя донные точки друг с другом или с ближайшей точкой на противолежащей стороне контура, можно найти разделение объекта на составляющие (рис. 20 б , 20 в ).

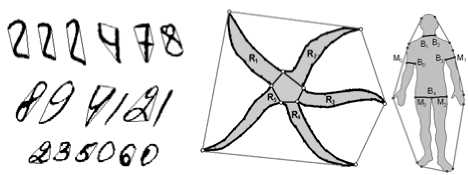
Рис. 20. Примеры приложений алгоритма поиска впадин. а) Впадины в рукописных цифрах. б), в) Сегментация с помощью донных точек впадин.

Соединяя донные точки друг с другом или с ближайшей точкой на противолежащей стороне контура, можно найти разделение объекта на составляющие. б) Выделение лучей морской звезды. в) Выделение конечностей человека

Впадины контура двумерной проекции трехмерного объекта обладают некоторой инвариантностью к повороту, а их относительная площадь (в сравнении с площадью объекта или его минимального объемлющего многоугольника) – к изменению размеров объекта (рис. 21).

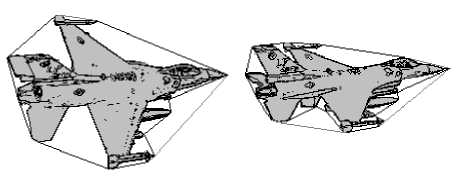
Рис. 21. Истребитель-бомбардировщик F-16.

Внешние отрезки ограничивают впадины, найденным с помощью минимального выпуклого многоугольника, внутренние отрезки – впадины, найденные с помощью рекурсивного поиска.

Взаимное расположение впадин и их относительная площадь обладают некоторой инвариантностью к повороту объекта

Вспомогательный алгоритм поиска минимального объемлющего выпуклого многоугольника так же может использоваться самостоятельно, поскольку в некоторых классах объекты имеют схожий вид не самой границы, а именно границы выпуклого многоугольника (рис. 22).

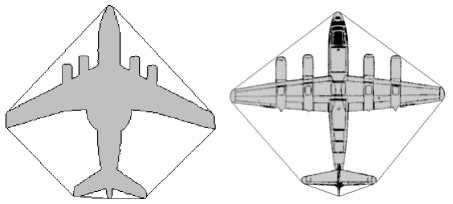
Рис. 22. Выпуклые многоугольники для видов самолетов сверху часто похожи на ромбы