Поисковая система Кортекс

1.    Общая характеристика индексной поисковой системы Кортекс

– Высокая степень параллелизма: разные запросы обрабатываются на разных процессорах (вычислительных машинах) и в то же время один запрос обрабатывается на многих процессорах. Последнее достигается за счет разделения индекса на многочисленные части, обработка запросов которых распараллеливается.

– Архитектура основана на использовании большого количества стандартных, недорогих ПК.

В результате система обеспечивает заданную производительность, имея стоимость намного меньшую, чем системы подобной производительности, построенные на мощных серверных станциях.

2.    Общая характеристика решаемой задачи

Рассматривается задача поиска, в которой обработка каждого запроса требует большого количества вычислений, в том числе обработки сотен мегабайт данных и выполнения нескольких миллиардов процессорных команд. Обработка пикового объема, характеризуемого тысячами запросов в секунду, могла бы потребовать использования дорогостоящих суперкомпьютерных вычислительных систем. Вместе с тем использование большого количества дешевых, быстро заменяемых ПК и программного обеспечения, позволяющего находить вышедшие из строя компьютеры, позволяет решить эту задачу значительно дешевле, чем путём использования меньшего числа дорогостоящих серверов.

Ниже мы рассмотрим основные факторы, определяющие архитектуру системы. Такими факторами являются энергопотребление и отношение цены системы к ее производительности. Первый фактор является ключевым в задачах больших масштабах, так как он определяет максимально допустимый размер центров обработки данных, ограниченных потребляемой мощностью и охлаждающими установками.

Поскольку система легко распараллеливается, что позволяет увеличивать ее производительность линейно, то такой показатель, как пиковая пропускная способность, является менее важным, чем критерий цена/производительность. Таким образом, Кортекс – это специализированная система, ориентированная для решения задач, связанных с массовой обработкой большого числа однотипных входов.

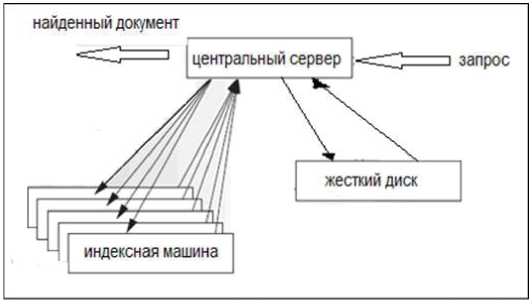
Рис. 1. Архитектура поисковой системы Кортекс

Ответ на запрос производится в результате его обработки на двух уровнях. На первом уровне производится распознавание слов запроса. На второй уровень поступает множество идентификационных номеров распознанных слов. Первый уровень представляет собой индекс слов, а второй уровень – индекс абзацев документов, где под документом понимается статья или книга, содержащаяся в электронной библиотеке.

Оба индекса имеют одну и ту же структуру и используют один и тот же рабочий алгоритм. Разница состоит только в формате входных данных. Входными элементами индекса 1-го уровня являются тройки букв слов. Например, для слова «являются» входными элементами будут «явл», «вля», «ляю», «яют», «ютс», «тся». Для алфавита из N букв число всех возможных троек и тем самым число входных адресов равно N3 . При этом адрес a, определяемый каждой тройкой букв xyz, вычисляется как a = asc(x) + asc(y) * N + asc(z) * N2 , где asc(L) — это ascii-код соответствующей буквы, а значение N = 256.

Число входов 2-го уровня троек и тем самым число входных адресов равно числу всех слов.

Рассмотрим способ распознавания образов, задаваемых наборами входных элементов.

Обратные множества

Для конечного набора конечных множеств { f } n , n Е N , набор обратных множеств { n } f , f Е F , был определен в [1] как

^{n} f = ^{{n : f Е {f}} n , n ^Е N ^{}                               (1)}

и назван индексом образов. Здесь N – множество индексов образов, а область определения F индекса образов - объединение F = D n { f }_n , n Е N , элементов исходных конечных множеств. Мы называем элементы f исходных множеств признаками образов, а нижние показатели n Е N именами образов.

Пример 1. Пусть дан следующий набор конечных множеств:

z = { a, c } , y = { b, c, d } ,u = { a, b } ,x = { a, d } ,v = { d } .

Тогда, в соответствии с определением (1), набор обратных множеств имеет вид a = {z, u, x}, b = {y, u}, c = {y, z}, d = {y, x, v}.

3.    Задача поиска

Пусть F n ,n E N , — это конечный набор конечных множеств. Для заданного конечного множества U требуется найти элемент m , такой что

D ( F m ,U ) = min D ( F n ,U ) .                           (2)

n E N

Здесь D(Fm, U) - это расстояние между множествами Fn и U, по аналогии с расстоянием Танимото, которое определяется как п (а т=      n(AnB)       = n(AnB)

T ⁽ , )    n ( A )+ n ( B ) - n ( A П B )    n ( A U B ) ,                  ⁽³⁾

где n – это количество элементов в множестве.

Исходя из предположения, что в решаемой задаче количество элементов во множествах одинаково, составим кортексное расстояние:

Dk ⁽ A'B ) = ^T a’XORb " ,                          (4)

n an ORbn где под n anXORbn понимается количество различных элементов в множествах A и B . Здесь anXORbn – логическая функция, принимающая значение 1 в случае, если an и bn различны, и 0, если они равны.

N – общее количество элементов в множествах A и B (при условии того, что эти количества равны).

4.    Уравнение поиска

Если неизвестный образ идентичен одному из образов-прототипов { f }_n , n E N , то правая часть выражения (2), описывающего задачу поиска ближайшего соседа, становится равной нулю. Будем называть уравнением распознавания следующее выражение:

D ( Fx,U ) = 0 .

Здесь U = { u } - неизвестный образ и F _x = { f } x - образ-прототип, служащий решением уравнения (5).

В [2] была доказана следующая теорема:

Необходимое условие того, что образ m является решением уравнения распознавания, состоит в том, что m принадлежит пересечению обратных множеств :

m E P| { n } f . f E{ u }

Здесь { n } f , f E F, — это обратные множества-прототипы { f }_n , n E N,F = U{ f }_n , n E N .

Если неизвестный (распознаваемый) образ не совпадает ни с одним из образов-прототипов { f }_n , n E N , то левая часть уравнения (5) всегда положительная. Однако образ F _x , при котором достигается минимум выражения (2), является наилучшим приближенным решением уравнения (5), поскольку выражение (2) является левой частью уравнения (5). Поиск минимума выражения (2) производится с помощью гистограммы образов.

5.    Гистограмма образов

Пусть H ( n,U ) — это гистограмма имен, содержащихся в обратных множествах { n } / , f € U .В [2] было доказано следующее утверждение:

Утверждение . Высота n -го отсчета гистограммы равна числу раз, которое имя n встречается в обратных множествах { n } / ,f € U .

Действительно, так как каждое обратное множество содержит не более одной копии каждого элемента, то общее число копий H ( n,U ) элементов n в обратных множествах { n } / , f € U ограничено размером множества U : H ( n, U ) <  | U |. Если элемент n встречается только в строгом подмножестве V С U, то H ( n,U ) = | V |, где | V | <  | U |.

Это утверждение лежит в основе эффективного алгоритма поиска решения путем вычисления гистограммы H (n,U ). При этом минимизация выражения min D (Fn,U) = D (Fn,U)                            (7)

n∈N производится путем нахождения максимума гистограммы H (n,U ), то есть n : H (n, U) = max H(n, U) .                              (8)

n ∈ N

Эффективность алгоритма распознавания, основанного на максимизации выражения (7), определяется следующими двумя условиями:

• (a)    { U } << N (количество элементов образа U намного меньше, чем общее число N образов-прототипов) и

• (b)    |{ n } / 1 ~ |{ f }_n| (среднее количество обратных образов приблизительно равно среднему количеству образов).

Если условия (a) и (b) выполнены, то вычисление гистограммы требует около | U | * |{ n } / | + | U | * |{ n } / | операций, необходимых для поиска максимума. Это число намного меньше, чем число операций | N | * |{ f }_n| , необходимых для сравнения всех прототипов с неизвестным образом. Заметим, что условие (a) справедливо для большинства приложений с большим числом прототипов, а условие (b) может быть удовлетворено путем агрегации нескольких признаков в один признак.

Можно показать, что если признаки х и у агрегируются в признак x + y * L , где L - это динамический диапазон исходных признаков, то величина |{ n } / | уменьшается в среднем до |{ n } / | /L . Если признаки х, у и z агрегируются в признак x + y * L + z * L 2 , то величина |{ n } / | уменьшается в среднем до |{ n } / | /L ² и т.д.

При переходе к нормализованной гистограмме

H ( n,U )

П^Г диапазон значений расстояний будет ограничен единичным интервалом [0, 1]. В этом случае расстояние, равное 1, означает, что множества Fn и U не имеют общих элементов, а расстояние, равное 0, говорит об идентичности сравниваемых множеств: Fn = U.

В практических задачах распознавания образов мы вводим порог распознавания T <  1, так что если расстояние D ( F _n , U ) < T , то образ F _n рассматривается как кандидат в ближайшие соседи. Окончательное решение относительно отобранных образов-кандидатов принимается путем их подстановки в выражение (2).

После того, как каждое слово запроса идентифицировано, найденные идентификаторы используются в качестве адресов индекса абзацев. На этом уровне локализация максимума выражения (2) позволяет найти идентификаторы абзацев, содержащих наибольшее число слов обрабатываемого запроса. Количество очков, набранных выделенными абзацами, равно значениям выбранных локальных максимумов гистограммы образов. Порядок вывода абзацев для просмотра производится в соответствии с набранными ими очками – от максимального значения до минимального значения.

6.    Общая характеристика вычислительного процесса поиска идентификаторов

Трудности при машинной реализации процесса поиска связаны с большим объемом данных. Документы библиотеки могут содержать сотни гигабайт данных и такой же объем данных будет содержать индекс абзацев. Поэтому индекс абзацев подразделяется на равные части, каждая из которых содержит соответствующую часть данных. При этом каждая часть индекса абзацев размещается в оперативной памяти отдельной машины. Центральный сервер передает запрос (набор идентификационных номеров слов запроса) по сети Ethernet одновременно на все машины. Слова запросов могут содержать орфографические ошибки, но так как идентификация слов индексом 1-го уровня основана на использовании гистограмм, то это позволяет в определенных границах производить точную идентификацию слов, несмотря на наличие незначительных ошибок. Каждая машина возвращает список очков, набранных максимально подходящими абзацами вместе с номерами этих конкурирующих абзацев. После этого центральный сервер выбирает абзацы-победители в соответствии с набранными ими очками. В завершение центральный сервер загружает абзацы соответствующих документов. Если одна из машин выходит из строя, то это событие идентифицируется с помощью центрального сервера, устанавливающего факт наличия возвращенного списка в ошибочном формате или факт отсутствия списка как такового, а вышедшая из строя машина заменяется общей резервной машиной.

С вычислительной точки зрения ускорение процедуры поиска достигается за счет того, что цикл поиска ответа в одном большом индексе сводится к множеству независимых коротких циклов, выполняемых параллельно в частях индекса, а результат поиска формируется с помощью простой в вычислительном отношении процедуры объединения частичных результатов. Поскольку короткие циклы выполняются независимо друг от друга и не обмениваются информацией, то ускорение почти пропорционально используемому числу коротких циклов. Другими словами, если производительность некоторых машин ниже средней, то это не повлияет на общую производительность системы, если обслуживаемую медленной машиной часть индекса разбить еще на несколько частей и увеличить число обслуживающих их машин. Решение задачи разбиения максимально упрощается тем обстоятельством, что индекс может разбиваться случайным образом на произвольное число частей.

Таким образом:

• –    в системе сознательно не используется дорогая аппаратура; при этом выбор процессоров производится в соответствии с критерием, выражаемым отношением: производитель-ность/цена, а не в соответствии с критерием максимального быстродействия процессора;

• –    использование обычных недорогих машин позволяет контролировать общую стоимость системы и увеличивать общий объем индекса без существенного увеличения общих затрат;

• –    надежность системы обеспечивается не за счет многократного резервирования аппаратуры, а за счет программного обеспечения мгновенно находящего вышедшую из строя машину и временного подключения вместо неё общей резервной машины, которая, после замены поврежденной машины, снова выводится в резерв; при этом физически резервные машины могут располагаться где угодно, а для её активации в неё передается маленькая часть индекса, которая обслуживалась поврежденной машиной (все машины получают свои частичные индексы с дисков центрального сервера);

• –    единственная дорогая аппаратная часть системы – это диски большого объема центрального сервера, на которых хранятся исходные документы (базы данных), содержание которых выводится на экран пользователей, а также хранятся все части общего индекса.

7.    Стоимостная структура системы

Как отмечено выше, инфраструктура системы состоит из большого числа недорогих персональных компьютеров. Машины с большой общей памятью наиболее эффективны в случае, когда при большой величине отношения вычислительной нагрузки к объему информационных потоков, или когда структура информационных потоков и структура обработки данных являются динамическими или трудно предсказуемыми. В Кортексе ни одно из этих условий не выполняется, поскольку индекс предсказуемо разбивается на части, которые не общаются друг с другом. Кроме того, в силу простоты программного обеспечения собственной разработки, передающего запросы машинам и получающего их ответы для анализа и выявления победителей, основные стоимостные затраты определяются количеством используемых машин и стоимостью их эксплуатации, а не стоимостью программного обеспечения. Также в больших машинах с разделенной памятью решение задачи выявления программно-аппаратных отказов отдельных частей является весьма сложной, а подобные отказы приводят к зависанию всей системы.

В результате использования в поисковой системе Кортекс большого числа недорогих микропроцессоров нежелательные эффекты, вызываемые отказами отдельных частей, не выходят за пределы отказавшей части и могут быть быстро устранены обслуживающим персоналом, что отвечает требованиям постоянной готовности системы к её использованию пользователями электронных библиотек.