Поле излучения двусторонней щелевой антенны
Автор: Войтович Николай Иванович, Клыгач Денис Сергеевич, Хашимов Амур Бариевич
Статья в выпуске: 23 (282), 2012 года.
Бесплатный доступ
Предложен метод расчета поля излучения двусторонней щелевой антенны. Для строгой электродинамической формулировки задачи используется лемма Лоренца и вспомогательная функция Грина. Показано, что поле излучения в дальней зоне определяется с помощью поля рассеяния плоской волны на пластине, которая служит для выполнения щелевой антенны.
Щелевая антенна, поле излучения, функция грина
Короткий адрес: https://sciup.org/147154772
IDR: 147154772 | УДК: 621.396.6(07)
Текст научной статьи Поле излучения двусторонней щелевой антенны
Щелевая антенна была предложена в 1938 г. Аланом Блюмлейном с целью применения в телевизионном вещании в диапазоне ультракоротких волн с горизонтальной поляризацией и круговой диаграммой направленности (ДН) в горизонтальной плоскости [1]. Антенна представляла собой продольную щель в трубе. Простота конструкции, отсутствие выступающей части над поверхностью, в которой прорезана щель, привлекли к ней внимание специалистов, проектирующих радиосистемы для подводных лодок. Щелевые антенны не нарушают аэродинамику объектов, на которых они установлены, что определило их широкое применение на самолетах, ракетах и других подвижных объектах. Такие антенны со щелями, прорезанными в стенках волноводов прямоугольного, круглого или иной формы поперечного сечения, широко используются в качестве бортовых и наземных антенн радиолокационных и радионавигационных систем. 1
В теории антенн используют понятие идеаль- ной щелевой антенны, под которой понимается щель в идеально проводящей, бесконечно тонкой плоскости. В ряде работ рассмотрены характеристики односторонней и двусторонней щелевой антенны на бесконечно протяженной идеально проводящей ленте. Конструкции используемых на практике щелевых антенн очень разнообразны.
2Как правило, в этих антеннах используются щели с односторонним излучением в открытое пространство. Теория антенн с односторонним излучением хорошо разработана и изложена в большом количестве журнальных статей, учебниках и монографиях. Однако в этих работах не рассмотрены особенности поведения фазовых ДН щелевых антенн. Необходимо подчеркнуть, что учет фазовых ДН имеет важное значение при анализе характеристик направленности антенных решеток, в которых двусторонняя щелевая антенна выступает как излучающий элемент. В качестве примера можно привести результаты исследования оригинальной щелевой турникетной антенны [2], преимущества которой в сравнении с аналогичны-
ми антеннами делают ее привлекательной для использования в системах с круговой зоной обслуживания при горизонтальной поляризации поля излучения. В данной статье в строгой электродинамической постановке получены соотношения и приведены примеры расчета комплексных ДН двусторонней щелевой антенны, выполненной на поверхности ограниченных размеров.
Физическая модель двусторонней щелевой антенны
Предположим, что имеется плоская бесконечно тонкая идеально проводящая пластина, ограниченная некоторым контуром, в общем случае произвольной формы, в которой прорезана щель (см. рисунок).
Точку O в центре щели примем за начало сферической системы координат ( r , 0, ф ) с единичными ортами ( i r , i 0 , i ^ ) и декартовой системы координат ( x , y, z ) с единичными ортами ( i x , i y , i z ) . Ось z направим параллельно продольной кромке щели. На поверхности щели S щ будем различать верхнюю сторону x = 0 + 0 и нижнюю сторону x = 0 - 0 . Будем полагать, что в щели известно распределение напряженности электрического поля E 0 = i y E 0 . При решении электродинамической задачи будем полагать, что в щели заданное распределение напряженности электрического поля может быть представлено сторонним магнитным источником j с m т , который образован двумя поверхностными магнитными токами: магнитным током j 1 ms , распределенным на верхней стороне x = 0 + 0, и магнитным током j ^s - на нижней стороне пластины x = 0 - 0 :
j lms = - i . x E o = - i z E 0 ;
j ms = - ( - i , x E o ) = i z E o .
Таким образом, электрические поля на верхней и нижней сторонах пластины синфазны между собой, а соответствующие им поверхностные магнитные токи противофазны. В соответствии с граничными условиями тангенциальная составляющая напряженности электрического поля на обеих сторонах поверхности пластины с заметаллизиро-ванной щелью равна нулю.
Определим ДН рассматриваемой двусторонней щелевой антенны.
Формулировка метода решения задачи
Для решения поставленной задачи воспользуемся интегральной формулировкой леммы Лоренца, которая представляет собой вспомогательное математическое соотношение, связывающее комплексные амплитуды двух электромагнитных полей.
В качестве первого поля рассмотрим искомое поле двусторонней щелевой антенны. Поскольку источники поля и идеально проводящая пластина расположены на конечном расстоянии от начала координат, то зависимость поля от расстояния при r ^ ю имеет структуру уходящей сферической волны [3]:
E = W H x r ;
Eо(О, ф) = WHф(0, ф) = exp(-ikr)
= E m 0 ; F 1 ( 0,ф)
kr
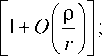
E ф ( 0, ф ) = - WH о ( О, ф ) = exp (- ikr) . .Г
= Em ф ' ) F 2 ( 0, ф ) 1 + O |Р|
kr L V r)
где H 0 , H ф - компоненты вектора напряженности магнитного поля H ; W = 120л Ом - волновое сопротивление свободного пространства; r – радиус-вектор текущей точки наблюдения: r = r 0 r ; r 0 – единичный орт радиуса-вектора точки наблюдения; к = 2л/Л. - волновое число; А - длина волны; F 1 ( 0,ф ) , F2 ( 0,ф ) - комплексные ДН, определяемые из решения задачи; р - наибольшее
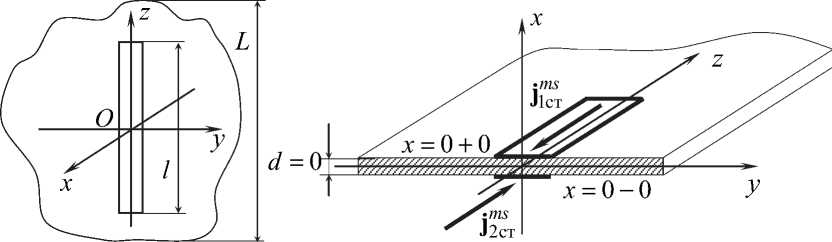
Геометрия двусторонней щелевой антенны
расстояние от начала координат, расположенного в области источников, до точки источника; O – символ Ландау.
Предположим, что в каждой точке некоторой области V , ограниченной поверхностью заметал-лизированной пластины S пл с щелевой антенной и поверхностью сферы S R , так что S = S пл + S R , определены электромагнитные поля E 1 , H 1 и E 2 , H 2 , создаваемые независимыми друг от друга распределениями объемных магнитных сторонних токов j 1 m ст , j 2 m ст (электрические источники отсутствуют).
В соответствии с леммой Лоренца векторы E 1 , H 1 и E 2 , H 2 связаны между собой следующим интегральным соотношением:
Ш E i х H 2 ) - ( E 2 х H i ) ] • n ds = S
= J (j™T • H2 - jmr • Hi) dv , (3) V где n – единичный вектор внешней нормали к поверхности S . Поля E1, H1 и E2,H2 в (3) удовлетворяют системе уравнений Максвелла и граничным условиям на поверхности S , однако, как следует из вывода леммы Лоренца, не обязательно должны удовлетворять условию излучения на бесконечности. Соотношение (4) будет справедливым и в том случае, если каждое из решений – E1, H1 или E2, H2– содержит одну плоскую волну или бесконечную совокупность плоских волн. Это замечание справедливо, потому что плоские волны, как известно, удовлетворяют системе однородных уравнений Максвелла, но не удовлетворяют условию излучения на бесконечности [3].
Далее будем полагать, что E 1 , H 1 является искомым полем, создаваемым рассматриваемой щелевой антенной с известным распределением магнитных токов j 1 m cт . Индекс 1 у векторов искомого поля опустим. Это поле удовлетворяет граничным условиям на поверхности пластины S пл и условию излучения на бесконечности. Будем считать, что поле E 2 , H 2 создано элементарным магнитным диполем j 2 m cт с единичным моментом, расположенным в точке r 1 :
j m cT = a 8 3 ( r - r i ) , (4)
где a – единичный вектор, задающий ориентацию вспомогательного источника; 8 3 ( r - r i ) - трехмерная S -функция.
Вспомогательное поле, обусловленное действием магнитного диполя j 2 m cт , обозначим векторами E ( m ) , H ( m ) . Подставляя (4) в (3), с учетом введенных обозначений получим:
a • H ( r i ) = - j • H ( m ) dv +
V
+ j [ ( E ( m ) х H ) - ( E х H ( m ) ) !• n ds . (5) s L' J
Как следует из (5), для того чтобы получить значение проекции искомого поля H(ri) в некоторой точке r1 на направление вектора a , надо в подынтегральных выражениях взять функцию Грина (E(m), H(m)), порождаемую источником (4), расположенным именно в этой точке r1 и ориен- тированным в направлении вектора a .
Функция Грина рассматриваемой задачи
Нас интересует ДН в дальней зоне, то есть поведение вектора h(ri) при ri ^^, поэтому целе- сообразно использовать функцию Грина, созданную бесконечно удаленным источником. Будем использовать в качестве функции Грина (E(m), H(m)) электромагнитное поле рассеяния на пластине плоской волны Hp = Hmp • exp (ik • r ) =
= ( i e H mp 0 + 4 H mp ф ) exP ( i k • r ) ; E p = W • r p х H p , где k – волновой вектор, характеризующий направление r p ( e p , ф p ) прихода плоской волны, k = krn = k (L sin0„ • cosф„ + i., sin0„ • sinф„ + pxp pyp p
+ i z cos 0 p ) (волна движется в направлении вектора - r p ). Плоская волна E p , H p является решением однородной системы уравнений Максвелла (без 8 -функции в правой части уравнений), поэтому во всех точках ограниченной части пространства слагаемое в левой части уравнения (5) оказывается равным нулю:
- j j m • H ( m ) dv = j [ ( E х H ( m ) ) - ( E ( m ) х H ) !• n ds . (6) V S ^'
Использование стороннего источника в виде плоской волны приводит к нарушению условия излучения. Однако, если функции E p = E mp • exP ( i k • r ) , H p = H mp • exP ( i k • r ) вычесть из функций E ( m ), H ( m ), то поле рассеяния
Es = E(m) - Ep, Hs = H(m) - Hp уже будет удовле- творять условию излучения, так как это поле является решением соответствующей корректной краевой задачи. Функцию Грина (E( m), H( m) ), получае -мую в результате решения задачи дифракции плоской волны на рассматриваемой пластине, представим в виде:
E ( m ) = E mp ■ exp ( i k ■ r ) + E 5 ;
H ( m ) = H mp ■ exp ( i k ■ r ) + H 5 .
Тогда выражение (6) для функции Грина (7) принимает следующий вид:
- J j m ■ H ( m ) dv = J [ ( E x ( H mp ■ exp ( i k ■ r ) + H , ) ) - VS
- ( ( E mp ■ exP ( i k ■ r ) + E 5 ) X H ) ] ■ n dS =
= f[(EXHmp ■ exp(ik^HEmp ^ exp(ik ^r)XH)]^nd5 +
+ J [ ( E x H 5 ) ) - ( E 5 x H ) ] ■ n ds . (8)
S
Поведение функции Грина в дальней зоне
Преобразуем слагаемые в подынтегральном выражении во втором интеграле в правой части (8), содержащие векторные произведения векторов E, H искомого поля и векторов Es , Hs поля рас- сеяния:
[(ExH5)-(E5 xH)] =
= W{Нx(Н5 xr)-Н5 x(Нxr)} == W{H5 (H■ r)-r(H5 ■ H)--H (H5 ■ r) + r (H5 ■ H )} =
= W { H 5 ( H ■ r ) - H ( H 5 ■ r ) } . (9)
Так как векторы Hs и Н в дальней зоне рас- положены перпендикулярно к направлению распространения r , то оба скалярных произведения и вместе с ними слагаемое в подынтегральном выражении поверхностного интеграла, содержащее поле рассеяния, обращаются в ноль. Следовательно, в дальнейшем при асимптотическом вычислении поверхностного интеграла (8) слагаемые с Es,Hs можно не учитывать. Тогда при вычислении поверхностного интеграла в функции Грина (E(m), H(m)) необходимо учитывать лишь слагаемые, включающие плоскую волну Emp,Hmp .
-Jjm■ Hm>dv = J [|exH VSпл + J [(ExHmp-exp(ik■r))-(Emp■ exp(ik■r)xH)]^nd- (10) SR Значение поверхностного интегралана внешней поверхности SR области V Вычислим поверхностный интеграл в (10) по поверхности SR , учитывая асимптотическое поведение искомого поля при большом значении kr : J[( ExHmpexP( ik■r))-EmpexP( ik■r)xH)]^nd 5 = SR = J [(EmxHmp)-(EmpxHm)]expOSpkilnd5, (11) . Em = E. F (6,. i6+ Em, F2 (6. i,; Hm = Hma F (6,,)i6+ Hm, F2 (6,,)i, - Подынтегральное выражение представляет собой произведение регулярной функции f (6, ,) = [(Emx Hmp )-( Empx Hm )] 'nkr и экспоненты, показатель которой есть произведение мнимой единицы, большого параметра Q = kr и действительной функции g (6,,) = r0 ■(rp - r0) -Раскрывая скалярное произведение векторов, получим: g (6,,) = sin 6 cos , sin 6p cos ,p + + sin 6 sin , sin 6p sin ,p + cos 6 cos 6p -1. (12) Функция g (О,,) имеет две стационарные точки: первая (6 = 6p,, = ,p), то есть при r = rp ; вторая (6 = л - 6p,, = л - ,p), то есть при r = -rp . Воспользуемся известными соотношениями для асимптотических вычислений кратных интегралов [4], определяемых вкладом n-й стационарной точки хС”)(n - номер стационарной точки): n2 In(^)=f (x^ exp (i^g (xCт))) ^"^J x x exp det d2g -12 dx dx xpст xqст p = 1, n; q = 1, n; o= jn; sign dp , p=1 где dp – собственные значения матрицы Гессе d 2 g xpст xqст 1x n ;1x n Таким образом, первая производная показателя экспоненты обращается в ноль в следующих двух случаях: r = rp и r = -rp Вычислим значение множителя l(Em xH )-(Em„xH )l в по-mmp mp m дынтегральном выражении в этих двух стационарных точках: [(Em X Hmp )"( Emp X Hm )] = = W [(( Hm X Г )x Hmp )-(( ГpX Hmp ) )x Hm )] = = W [-Hm (Hmp ■ Г ) + Г ( Hmp ■ Hm ) - -Hmp ( Hm ' rp ) + rp ( Hmp ' Hm )] = = W [-Hm (Hmp ■ r )- Hmp ( Hm ' Гp ) + +(Гp + Г) ( Hmp • Hm )] . (14) В дальней зоне H mp 1 rp , H m 1 r , поэтому при r H rp H mp ■ r = 0, H m ■ rp = 0. Следовательно, [(EmXHmp)-(EmpXHm)] = W(rp + r)(Hmp ■ Hm). (15) В первой стационарной точке r=rp , тогда значение подынтегральной функции f (0,р) = [(Em XHmp HEp XHm )}n/kr=2WHp• Hm/k. Во второй стационарной точке r = -rp , тогда f (о,р) = 0 . Следовательно, из двух стационарных точек только первая дает вклад в интеграл порядка 1 kr , вклад второй точки имеет значение не выше 1)(kr )2 и в дальнейшем учитываться не будет. Вычислим детерминант матрицы Гессе в первой стационарной точке: д2 g(о ф)/ао2| д2g(о ф)/дфдо 1 °™p >ф=<рp н д2 g (°, Ф)/додр д2 g (°, ^Nl, 1 о=°p ,р=Фp " -1 0 0 -sin2 0p =sin2 °p. Собственные значения матрицы Гессе в первой стационарной точке равны: X1 = -1; X2= - sin20p; о = signX1 + signX2= -2. Следовательно, асимптотическое значение интеграла по внешней поверхности области V равно: 11(Q) - 2Wr ■(Hmp ■ Hm )X 2л exp (-i л/2) 2 . X-----------------r2 sin 0„ ■ r = ( kr )2 sin 0p = -i4лW (Hmp ■ Hm ) -V. (17) k2 Значение поверхностного интеграла на внутренней поверхности Sплобласти V Рассмотрим поверхностный интеграл по внутренней поверхности Sпл области V , в качест- ве которой в нашей задаче выступает поверхность пластины Sпл с заметаллизированной щелью: J (EXH(m))-(E(m)xh) ■ nds = Sпл J [(nX E)] ■ H(m) ds - J [(n XE(m) V V L x пл пл ) ■ H ds. (18) По предположению пластина обладает иде- альной проводимостью, следовательно, (n X E) = 0, тогда первый интеграл в правой Sпл части соотношения (18) равен нулю. В общем случае в лемме Лоренца искомое и вспомогательное поле вводятся как поля, возникающие при расположении произвольных объектов в поле заданных источников. Будем полагать, что вспомогательное поле E(m), н(m) формируется в результате ди- фракции на той же пластине, на которой расположена щель с заданным распределением напряженности электрического поля. Подчиним тангенци-(m) альную компоненту вектора E вспомогательно- го поля тем же граничным условиям, которым удовлетворяет тангенциальная компонента искомого поля: (nXE(m)) = 0 . Тогда и второй инте- Sпл грал в правой части соотношения (18) будет равен нулю. Таким образом, поверхностный интеграл по внутренней поверхности области V равен нулю. Проводя вычисления поверхностного интеграла аналогично тому, как это выполнено в предыдущем пункте, получим: i[(E! "’XH„)-(E„ X H< m>)] expfiikrr^krl ds . - 2Wr-( H,.H 1) 2-L exP^ ,. sin 0p .r= \ / (kr)2 sin 0p = -i4лW(Hmp.H<m))k2. (19) Значение объемного интеграла Обратимся теперь к вычислению объемного интеграла в выражении (10). По исходным предположениям в области V действует сторонний источник jcmm , включающий в себя поверхностные токи j1ms и j2ms (см. рисунок), так что jms = jT8(x + 0) + jms8(x - 0). При этом поверхностные токи j1ms и j2ms представляются как предельные значения объемной плотности тока jcmт при стремлении координат источника к поверхности пластины. Поскольку j m5=-”, то объемный интеграл равен: J jm • H<m Idv = V = J j” •(Hm)(0 + 0,y,z)-H(m)(0-0,y,z))dSщ. (20) Sщ Подставляя в этот интеграл асимптотические значения интегралов по внешней и внутренней поверхности области V , получим: i2uW( Hmp • Hm ) k = = J jm •(Hm)(0+0,y,z)-Hm)(0-0,y,z))dSщ (21) Sщ или, с учетом представления полей в виде (11), k2 ( Hmp0 HmO F(0, ф) + Hmpф Hmфl F2(0, ф)) = -i—— X х J j” •(H Sщ Из соотношения (22) видно, что для выделения ДН F1 (е, ф) необходимо в качестве вспомога- тельного поля выбрать (iфEmpф , ieHmpе), при Empе = 0; Hmpф = 0; Hmp0 = 1 , плоскую волну этом Emp ф = 1; в качестве функции Грина выбрать функцию (Еф”), Hm)) - поле дифракции выбранной плоской волны на идеально проводящей пластине. Тогда в левой части соотношения (21) останется только слагаемое, содержащее функцию F1 (0, ф): k2 F1(0,Ф) = -i —х 2uW х J jm5 •(Hm)(0 + 0,y,z)-Hm)(0-0,y,z))dSщ. (23) Sщ Для определения ДН F2(0, ф) необходимо выбрать плоскую волну (iеEmpе, iфHmpф) , при этом Empе = 1; EmpФ = 0; Hmpф = 1; Hmp0 = 0 , а в качестве функции Грина выбрать функцию (Egm), нф”)) - поле дифракции выбранной плоской волны на идеально проводящей пластине: k2 F2(0,Ф) = -i ^ ,,.х 2uW j1ms и поле, создаваемое плоской волной при дифракции на пластине. Согласно этим формулам, если известно поле HО”)(z, y) или нфm)(z, y), создаваемое в месте расположения источников j1m при дифракции плоской волны, падающей на пластину с некоторого направления, то в этом направлении амплитуда сферической волны, создаваемой источниками в присутствии пластины, находится как интегральная сумма всех полей на одной и другой стороне щелевой антенны с весовыми коэффициентами, равными плотности магнитного тока j1ms . Узкая щель Рассмотрим частный случай, когда щель является бесконечно узкой: jm5 = izIm (z)8(y - 0),(25) тогда выражение (24) принимает следующий вид: 2 l2 F2(e,ф)=-i-k-,J iz • Im(z)Гнфй| (x=0+0,y=0,z)-4n:W -1,2 l1' -Hm (x=0-0,y=0,z)]dl, где l – длина щелевой антенны. Рассмотрим поведение решения задачи дифракции при увеличении продольного размера L пластины (см. рисунок). Пусть плоская волна падает нормально к поверхности пластины (op = л/2), определим поле дифракции только в плоскости z =0. С увеличением продольного размера пластины вклад ее торцевых участков и прилегающих к ним областей в формирование поля рассеяния в плоскости z = 0 будет быстро убывать. Тогда правомерным становится предельный переход к двумерной плоской задаче для нахождения поля дифракции. Если при увеличении продольного размера радиус удаленной сферы R » l то электромагнитное поле имеет вид расходящейся сферической волны. Следовательно, все условия корректного предельного перехода будут обеспечены. В предельном случае для поля дифракции выполняются следующие условия (напряженность магнитного поля неизменна вдоль щелевой антенны): Hфm) (x = 0+0,y = 0,0)= izH(”) (x = 0+0,y = 0,0); (27) HфmJ (x = 0 - 0, y = 0,0)= izHфm) (x = 0 - 0, y = 0,0), где H ) - поле дифракции плоской волны на ленте. Тогда F2(0, ф) = - - k2A ----х 4л W х[Hфm)(x = 0 + 0,0,0)-Hфm)(x = 0 - 0,0,0)], (28) l2 где A = J I(z) dz. - M г Таким образом, в рассматриваемом частном случае значение ДН двусторонней щелевой антенны в заданном направлении пропорционально разности значений напряженности магнитного поля в двух точках, расположенных друг напротив друга на противоположных сторонах щели при падении плоской волны с этого направления. Выводы 1. С применением леммы Лоренца получены соотношения для вычисления комплексной ДН двусторонней щелевой антенны на идеально проводя-щей пластине. В качестве функции Грина применено строгое решение задачи дифракции плоской волны на идеально проводящей пластине. Полученные соотношения применимы для случая произвольной формы контура пластины, произвольной поляризации поля и 2. В частном случае, когда бесконечно узкая щель расположена на идеально проводящей бесконечно тонкой ленте, значение ДН в заданном направлении в плоскости, ортогональной оси щели, пропорционально разности значений напряженности магнитного поля в двух точках, расположенных друг напротив друга на противоположных сторонах щели, при падении плоской волны на ленту с этого направления.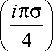
Список литературы Поле излучения двусторонней щелевой антенны
- Британский патент № 515684. HF electrical conductors/Alan Blumlein, -Опубл. -1938. -5 с.
- Пат. 2401492 Российская Федерация, МПК7 H 01 Q 13/00. Широкополосная турникетная антенна/Н.И. Войтович, Д.С. Клыгач, Н.Н. Репин. -№ 2009133771/07; заявл. 08.09.2009; опубл. 08.09.2009, Бюл. № 28. -18 с.
- Ильинский, А.С. Математические модели электродинамики/А.С. Ильинский, В.В. Кравцов, А.Г. Свешников. -М.: Высш. шк., 1991. -224 с.
- Фелсен, Л. Излучение и рассеяние волн: в 2 ч./Л. Фелсен, Н. Маркувиц. -М.: Мир, 1978. -Ч. 1. -547 с.


