Поле равномерно и прямолинейно движущегося электрического заряда

W = mc масса этого поля будет равна m = —^1 u ( x, y, z ) dV , которая c ²

определяет его инерционные свойства.

Для покоящегося точечного заряда q известно, что напряженность электрического поля равна

E = ^2

,

r а скалярный потенциал

q

ф = - , r

где r – расстояние от заряда q до рассматриваемой точки поля, в которой определяются значения E и φ .

Законы изменения величин E и φ от расстояния r определяются объемной плотностью энергии u ( x , y , z ) электрического поля. Под объемной плотностью энергии u ( x , y , z )

электрического поля зарядов мы не понимаем известное в 12

электродинамике выражение E , которое, как мы считаем, 8π выражает объемную плотность энергии взаимодействия электрических зарядов, образующих данное поле.

Электрическое поле неподвижного заряда устойчиво, оно не меняется со временем и для точечного заряда сферически симметрично. Если передвинуть заряд из одного положения 1 в другое – 2, рис. 1, в котором он также будет неподвижным, то в процессе такого перемещения его электрическое поле будет деформировано в силу конечности скорости передачи электрического возмущения. Но по прошествии некоторого времени электрическое поле заряда q в положении 2 примет прежний вид, описываемый формулами (1) и (2). Это произойдет под влиянием тех процессов перераспределения объемной плотности u ( x , y , z ) энергии электрического поля, которые приведут ее к прежнему выражению для неподвижного заряда.

Рис. 1

Значение величины скорости возмущения электрического поля в настоящее время неизвестно, поскольку не было прямых соответствующих опытов по ее измерению. Принято считать, что эта скорость равна скорости света. Но это произвольное допущение, не подкрепленное опытом. Известно, что свет – это поток большого числа фотонов, летящих со скоростью света. Но скорость передачи возмущения собственно материальной среды электрического поля может быть отличной от скорости света, что необходимо проверить на опыте.

Если вывести заряд q из положения покоя и сообщить ему некоторую скорость v за время τ , то в процессе ускорения заряда его электрическое поле окажется деформированным. Но эта деформация поля начнет уменьшаться после прекращения ускорения заряда q и через некоторое время полностью исчезнет. Это исчезновение деформации поля после прекращения ускорения заряда обусловлено теми же причинами, что и для случая, показанного на рис. 1. В деформированном электрическом поле заряда, движущегося с постоянной скоростью, после прекращения его ускорения возникнут процессы, приводящие объемную плотность энергии u (х, jy, z) к устойчивому состоянию. На элементарные объемы этого деформированного поля, видимо, действуют некоторые силы, приводящие структуру поля к своему прежнему состоянию. Электрическое поле ускоренно движущегося заряда оказалось деформированным, как уже указывалось, из-за конечной скорости передачи изменения объемной плотности u(х, jy, z) энергии этого поля. Естественно предположить, что в деформированном таким образом электрическом поле, возникли силы, действующие на все его элементарные объемы Л V. После прекращения ускорения заряда эти силы восстанавливают прежнюю структуру поля в собственной системе отсчета K ‘, движущейся со скоростью заряда относительно неподвижной системы отсчета K. В результате чего электрическое поле заряда, движущегося с постоянной скоростью, в собственной системе отсчета K' будет таким же, как и при неподвижном заряде относительно системы отсчета K, т.е. сферически симметричным. В системе отсчета K, относительно которой заряд движется с постоянной скоростью, для величин E и ф в рассматриваемых точках А 1 и А2 эффекты запаздывания будут отсутствовать, рис. 2.

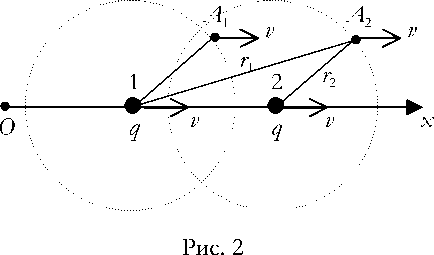
После прекращения ускорения заряда и выравнивания объемной плотности u ( х , у , z ) энергии в собственной системе отсчета K' электрическое поле становится сферически симметричным и каждый элемент его объема движется с той же самой скоростью, что и заряд q . Поскольку заряд q в точках 1 и 2 имеет одну и ту же скорость v и такую же скорость имеют все точки электрического поля, то расстояние Лх = v ( 1 ₂ — 1 1 ) будет равно 94

расстоянию A ₁ A ₂ , которое пройдет точка A ₁ за то же самое время ( 1 2 — 1 1 ) • Следовательно характеристики электрического поля при положениях заряда q в точках 1 и 2 будут одинаковыми, т.е. E 1 = E 2 , ф 1 = ф 2 , что обусловлено одновременным движением заряда и всех точек его электрического поля с одинаковой скоростью.

Если обозначить расстояние от точки 1 до точки A ₂ через r ₁ , а расстояние от точки 2 до точки A ₂ через r ₂ , то значения для E и φ

в точке A 2 запишутся в виде:
заряд находится в точке 1 :	E 1	q 2 r 1	, φ 1	= q- • r 1	(3)
заряд находится в точке 2 :	E 2	q 2 r 2	, φ 2	= q r 2	(4)

Как видно из этих выражений, являющихся математической записью приведенных выше рассуждений, запаздывающие эффекты в них не содержатся. А это значит, что преобразования Лоренца, полученные им при вычислении скалярного потенциала φ движущегося с постоянной скоростью электрического заряда [1, стр. 165], являются не соответствующими физической реальности. Вследствие чего Специальная Теория Относительности (СТО), использующая эти преобразования, как свою фундаментальную основу, является ложной теорией. Причина, по которой в физику были внедрены ложные преобразования Лоренца, проста – неучет того обстоятельства, что заряд и все точки его поля движутся с одинаковыми скоростями в случае, когда движение заряда равномерно и прямолинейно.

Ввиду важности приведенного заключения, проясним этот вопрос еще раз, рис. 3.

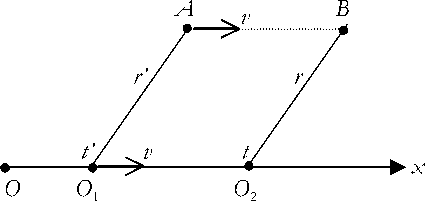
Рис. 3

Как уже было описано выше, все элементарные объемы электрического поля, движущегося с постоянной скоростью заряда, движутся с той же скоростью, что и сам заряд. Пусть в момент времени t' заряд находился в точке O 1 и его потенциал в точке A q равен фA = — , r = O 1 A. Через некоторое время Лt заряд r′ переместился в точку O2 . За это же время элементарный объем Л V электрического поля в точке A переместился в точку B. Так как скорости движения заряда q и объема Л V вокруг точки A одинаковы, то O 1 O2 = AB и O 1 O2//AB . Отсюда следует, что контур O 1 ABO2 является параллелограммом, в котором OA = O2B = r. Элемент объема Л V вокруг точки A переместится за время Лt в q неподвижную точку B, следовательно фA = фB = — и никакого r запаздывания здесь нет.

Для заряда, движущегося прямолинейно и равномерно, скалярный потенциал Льенара-Вихерта [1, стр. 164] в точке A ( x , y , z ) , рис. 4 , имеет вид

q          1

ф ( x , y , z , t ) =---.

4 ПЕ ₀ r' — ( v • r ' / c )

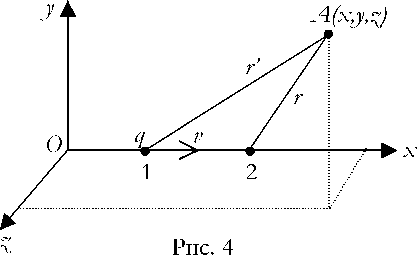
В момент времени t' заряд q находился в точке 1, а в момент времени t — в точке 2. Расстояние от точки 1 до неподвижной точки A ( x , jy , z ) равно r ‘ , а от точки 2 до A равно r . Моменты времени t' и t связаны соотношением

r

t = t--.

c

В выражении (6) предполагается, что возмущение электрического поля распространяется по прямой 1A . Учитывая скорость движения заряда, найдем расстояние r' = (x — vt ')2 + jy2 + z2 . (7)

Разрешая уравнения (6) и (7) относительно t ' и r' и подставляя их в (5), Фейнман [1, стр. 164] для движущегося с постоянной скоростью заряда получает выражение скалярного потенциала в точке A

Ф ( ^x , y, Z, t) =

q

4 πε ₀

v

^^^^^^^в

2 c

( x — vt ) 2

1 — v / c

+ y + Z

1/2

Для заряда, находящегося в начале координат собственной системы отсчета, скалярный потенциал имеет вид q1

^{Ф (} x ’ y ’ z) ⁼ ^T'    2^ 2^ 21-/2 .

4 П£ о [x + jy + z ]

Из сравнения выражений (8) и (9) вытекают известные преобразования Лоренца. Выше мы уже указали, что эти преобразования Лоренца не соответствуют физической реальности, так как при выводе выражений (5), (8) и (9) не учитывалось движение самого поля. По этой причине и выражение для скалярного потенциала Льенара-Вихерта произвольно движущегося заряда является неверным. Чтобы получить правильное выражение скалярного потенциала для произвольно движущегося электрического заряда, необходимо учесть :

• 1)    движение самого электрического поля, элементарные объемы которого будут двигаться с разными ускорениями, зависящими от запаздывания возмущения поля в данную его точку ;

• 2)    распространение возмущения поля происходит не в неподвижной системе отсчета, относительно которой движется заряд, а в собственной неинерциальной системе отсчета, так как возмущение поля представляет собой изменение объемной плотности u ( x ', y ', z ') энергии поля в собственной системе отсчета материальной среды, являющейся носителем электрического поля.