Полет насекомых

Вначале рассматриваются пчелиные соты и доказывается, что над ними пульсирует тепловой поток энергии и этим объясняется некоторые свойства пчелиных сот. Поскольку они являются частным случаем полостных структур, последнее утверждение распространяется на все плоские полостные структуры (ППС). Далее показывается, что, если ППС начинает двигаться, то появляются силы Кориолиса, которые поднимают и ускоряют движение ППС. Показывается, что тепловой поток над ППС и силы Кориолиса создаются гравитационной энергией Земли.

Оглавление

• 1.    Вступление

• 2.    Предпосылки

• 3.    Геометрия пчелиных сот

• 4.    Гравитационное поле пчелиных сот

• 5.    Моделирование

• 6.    Предположение о механизме влияния поля на биообъекты

• 7.    Пульсирующий поток энергии над полостными структурами.

• 8.    Движение ППС

• 9.    Полет насекомых

• 10.    Математическая модель полета ППС

Литература

1.    Вступление

Эта статья фактически является продолжением статьи [16]. Для удобства читателя здесь вначале приведены разделы этой статьи, а еовые разделы продолжают нумерацию.

Показывается, что в окрестности пчелиных сот существует немонотонное гравитационное поле. Рассматривается структура

Доклады независимых авторов 2024 выпуск 59 этого поля. Предполагается, что это поле является причиной специфического воздействия пчелиных сот на биологические объекты. Описывается возможный механизм воздействия этого поля на биологические объекты.

"К настоящему времени в естествознании накопилось достаточно много наблюдений, свидетельствующих о существовании специфического воздействия, которое оказывают на биообъекты полостные структуры (пирамиды, пчелиные и подобные им соты, пористые материалы и т.п.)" [1]. Такие воздействия проявляются наиболее ярко у пчелиных сот. Например, в [2] пчеловод пишет : "Ячеистые структуры типа пчелиных сот создают поле, которое угнетает жизнедеятельность микробов и даже корней растений, благодаря чему гнезда ос и пчел всегда чисты. Если пчелиные соты без меда подержать над головой человека, то через несколько минут у него исчезнет чувство усталости и головная боль, нормализуются кровяное давление, сон." В [3, стр. 205] отмечается "... любопытнейшее явление у иных испытуемых — так называемые фосфены: подвижные, постоянно меняющиеся яркие разноцветные узоры при закрытых (а иногда и открытых) глазах — то всполохи, вспышки, искры, то струящиеся волны и спирали, то сложнейшие геометрические построения удивительной красоты, ни на что природное не похожие" — см. рис. 0. Разнообразные явления вблизи пчелиных сот описываются в [4].

Рис. 0.

Из сказанного следует, что в окрестности пчелиных сот существует некоторое поле, являющееся активным источником воздействий на биологические объекты. Далее исследуется природа такого активного поля. Отметим, что известны работы, в которых рассматриваются различные гипотезы о природе этого поля — см. [1] и ссылки в этой работе, [9-11]. Предлагаемая гипотеза отличается тем, что позволяет получить некоторые количественные оценки.

2.    Предпосылки

Существование гравитационных волн предсказывается общей терией относительности. Из нее следует, что при слабых гравитационных полях и малых скоростях гравитация описывается максвеллоподобными уравнениями. Именно такие условия существуют на Земле. Следовательно, должны были бы наблюдаться гравитоэлектромагнитные        эффекты,        аналогичные электромагнитным эффектам.

Рассмотрим уравнения электростатики, которые имеют вид (здесь и далее используется система СГС):

div# = 4яр ,                                          (1)

rot# = 0 ,                                                  (2)

где

• •    р — плотность электрического заряда V г • см / см ³ ;

• •    q —электрический заряд [V г • см ] ;

• •    Е — напряжённость электрического поля [V г • см / сек ²] ;

Из [5] следует, что имеют место также уравнения гравитостатики вида div#g = 4nGpg,                                     (3)

rot# g = 0 ,                                              (4)

где

• •    Pg — плотность массы [ г/см³];

• •    m —масса [ г ];

• •    #д — напряжённость гравитоэлектрического поля [см/сек²];

• •    G - гравитационная постоянная, G ~ 7 • 10^-8[см³/г • сек²].

3.    Геометрия пчелиных сот 4.    Гравитационное поле пчелиных сот

Пчелиные соты (см. рис. 1) состоят из довольно тонких, близко расположенных друг к другу пчелиных ячеек. Толщина сот с незапечатанным расплодом составляет около 22 мм. Пчелиная ячейка имеет шестигранную форму и характеризуется следующими размерами: глубина 11-12 мм, диаметр вписанной окружности 5.375.42 мм, объём около 0.28 см3. Стенки ячеек имеют толщину примерно 0.1 мм. Отклонение от этой усредненной величины может быть не более 0.002 мм. На 1 см2 приходится около четырех ячеек [6].

Плотность воска примерно 1 г\ см3.

Рис. 1 (из [2]).

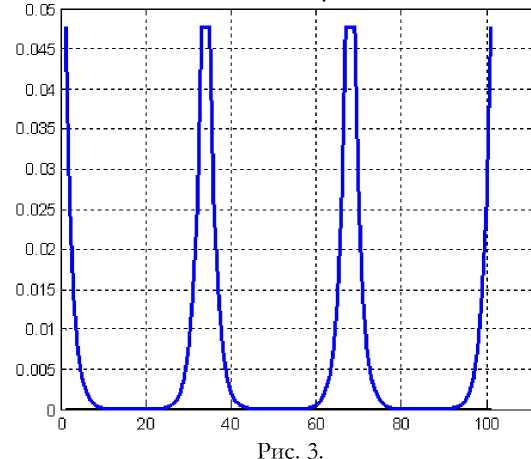
На рис. 2 показан фрагмент пчелиных сот в декартовых координатах X, у, z и плоскость ABCD в координатах XOZ , перпендикулярная плоскости сот. Мы будем определять векторы гравитационных напряженностей Е д _Х , Е ду , E_gz , создаваемых массами пчелиных сот. Для этого надо решить уравнения (2.3, 2.4) при известной функции р_д (х, у, z) распределения плотности масс в пчелиных сотах. В частности, эта функция распределения плотности масс по оси оу при X = 0 и z = 0 на рис. 2 - Р д (0, У, 0) имеет вид, представленный на рис. 3. Здесь предполагается, что соты являются достаточно глубокими и массы расположены, фактически, на шестигранной решетке.

Такая функция Р д (0, У, 0) может быть апроксимирована функцией вида Ch(^y) , где ^ - некоторый коэффициент, зависящий от диаметра ячейки. При этом функция Р д ^(0, У, ⁰⁾ в целом апроксимируется периодической функцией Chd(^y) , составленной из функций Ch(^y) , определенных на отрезке ye (-R,R) , равном ширирне ячейки. Аналогично может быть определена функция Shd(^y) , составленная из функций Sh(^y) , определенных на то же отрезке y e (-R, R) . Для дальнейшего важно отметить, что __________ 131

Dk hdGSy) = Shdcm £shdGSy) = chdm          (1)

A   E gx    x

z

B

E gy

D

Egz

Рис. 2.

Аналогично определяется функция P_g(o,o, z) . При этом функцию распределения плотности масс в пчелиных сотах можно определить формулой

P g ⁽x, y, z⁾ = ^ ^ Chd(^y⁾Chd(^z⁾5(x⁾ . (2)

Здесь предполагается, что X = 0 на дне ячеки, а функция

• 1,    если X < h,

8(х) = j                 '[                                 (3)

О, если X >  h, где h - высота ячейки,

Р - известный коэффициент (от него зависит толщина стенки в функции СН — см. также рис. 2), р₀ - плотность воска.

В [7, 8] дано решение уравнений вида (2.1, 2.2) при условии вида (2). В следствии указанной в п. 2 аналогии между электростатикой и гравитостатикой это решение может быть распространено на уравнения (2.3, 2.4, 2, 3). Тогда имеем:

Едх(х, у, z) = е • Chdtfy)Chd(Pz) cos(Дх),(4)

^ду(х,у, z) = е • Shd(Py)Chd(Pz) sin( fix'),(5)

EgZ(x, у, z) = е • Chd(Py)Shd(Py) sin( fix'),(6)

е = 4nGp0 h.(7)

Таким образом, при указанных условиях плоскость ячеек формирует поле напряженностей (4, 5, 6), которые гармонически изменяются в направлении ox . Будем говорить, что в направлении, перпендикулярном плоскости ячеек, формируется немонотонное гармоническое поле.

N

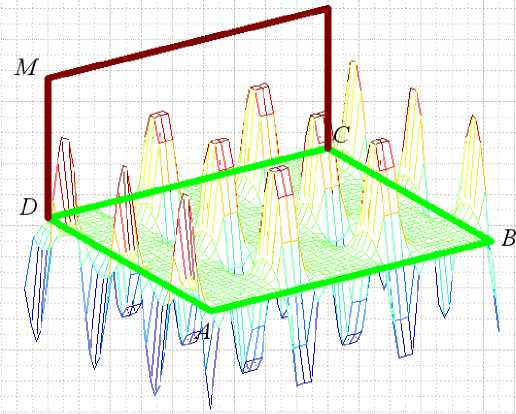
Рис. 4.

На рис. 4 показано для примера гармоническое поле напряженности Едх(х, у, z = 0)    на плоскости ABCD, перпендикулярной плоскости сот ACNM — сравни с рис. 2. На рис. 4 показаны значения напряженности (отложенные по вертикали). Но вектор этой напряженности направлен вдоль плоскости ABCD параллельно стороне CB. Это поле является статическим. Очевидно, должен быть период формирования этого поля и в этот период существует волна. У этой волны вектор напряженности Едх направлен в сторону распространения волны - от сот. Следовательно, такая волна является продольной.

Пример. Из раздела 3 следует, что высота ячейки h = 1.2 [ см ] .

В соответствии с (7) имеем е = 4nGpoh = 4п • 7 • 10-8 • 1 • 1.2 » 10-6[см/сек2].

Следовательно, в точке максимума гравитационная напряженность Етах ~ 10-6[см/сек2]. Для сравнения заметим, что масса 1г (что равно массе ячейки) на расстоянии г = 3[см] создает напряженность

4nG 4л>7^10^-8

10 ⁷[ см / сек ²] .

р =   =------ г     Г2         9

Эта напряженность р меньше напряженности Е. Кроме того, напряженность р (в отличие от напряженности Е) с расстоянием уменьшается резко и монотонно.

5.    Моделирование

Решение, найденное в предыдущем разделе, справедливо в близкой окрестности плоскости сот, поскольку не учитывает ограниченности этой плоскости и связанные с этим краевые эффекты.

В [7] дано решение подобной задачи электростатики 1) с учетом краевых эффектов и 2) при произвольной функции распределения зарядов вдоль ширины плоскости. Применим это решение к нашей задаче в частном случае, когда значение координаты z фиксировано.

Рассмотрим вектор-функцию

Е = [Е , ⁽х, у), Е , ⁽ х, у)]

и функционал вида

/1 к (2^. . ^д2Ев.\ .1г    ^Евх . дЕх

2^ЕЗУ' { _д у 2 ⁺ дхду ^{) +} 2^Е9^хЕ ду 2 ⁺ дхду

р(^Е) = я ,,.

+Е .( ^д2Ез^х ₊ ^д2ЕаЛ _ _Е . ( ^д2^Ев^у , ^д2Ев^у

■) dxdy ,

<> ^х [ д, 2 ⁺ дхду ) ^Е [ д, 2 ⁺ ду 2 .

\        +4'Gp_s■(^д ^X^X + ^)

где Р д (х, у) - известная функция. Градиент этого функционала имеет

вид +Ft + Ft +  + ^^-(/ + т)\ ду2 дхду дхду дх2           дх ду 1          (дЕх + д2Ех _ д^Еу _ д2Еу\ V            ду2   дхду дх2 дхду ’ При спуске на функционале (9) по градиенту (10) находится оптимальное значение функции (8), удовлетворяющее уравнению

р = 0 .                                                               (11)

Поскольку поле Е не имеет постоянной составляющей, то из (10, 11) следует (2.3, 2.4). Таким образом, спуск на функционале (9) по градиенту (10) при данном Р д (х, у) приводит к решению уравнений (2.3, 2.4).

В [7] описывается метод программная реализация такого метода решения этих уравнений. Далее мы только приведем расчет поля на этой программе. На рис. 5 показан результат расчета поля Едх(х> У,z = 0) трех ячеек ячеек на той же плоскости ABCD. На рис. 6 показано для наглядности это же поле со знаком минус.

-5

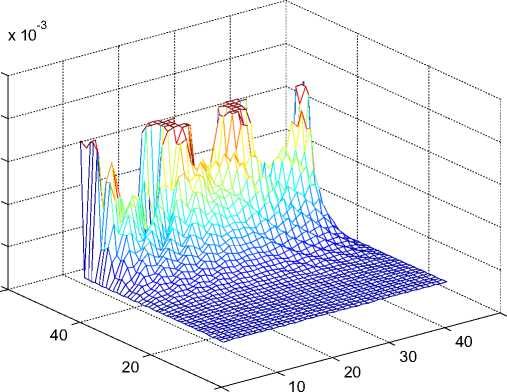
ех(х,у)-->у

Рис. 5.

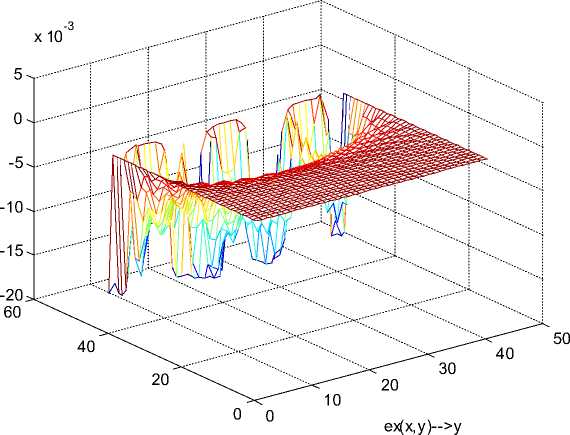
Рис. 6.

6.    Предположение о механизме влияния поля на биообъекты

Рассмотренное немонотонное поле модулирует постоянное поле притяжения Земли. Поэтому суммарное поле имеет немонотонный градиент. Подвижная масса, оказавшаяся в таком поле, смещается в ближайщую точку с нулевым градиентом. Если эта подвижная масса является, например, микроорганизмом, то его подвижность ограничивается. Жизнедеятельность такого обездвиженного микроорганизма ограничивается и он погибает. Так можно объяснить (отмеченный выше) факт угнетения жизнедеятельности микроорганизмов в окрестности пчелиных сот.

Подвижные частицы в теле человека под действием данного поля также стремятся расположиться в точках с нулевым градиентом. Таким образом, напряженность гармонического поля уменьшает тепловой хаос подвижных частиц, создавая некоторую упорядоченность. Видимо, именно это благотворно влияет на самочуствие человека вблизи пчелиных сот.

7.    Пульсирующий поток энергии над полостными структурами

Из предыдущего следует, что немонотонное статическое поле создает неравномерное распределение частиц воздуха по скоростям телового движения: в областях с меньшим гравитационным градиентом скорости молекул меньше, чем в обастях с бОльшим гравитационным градиентом.

Следовательно, в областях с меньшим гравитационным градиентом температура меньше, чем в обастях с бОльшим гравитационным градиентом. Следовательно, в областях с меньшим гравитационным градиентом возникает тепловой поток, направленный в сторону плоскости сот, а в обастях с бОльшим гравитационным градиентом возникает тепловой поток, направленный вверх от плоскости сот.

Тепловой поток, направленный в областях с меньшим гравитационным градиентом в сторону плоскости сот, повышает температуру охлажденных молекул воздуха, которые вновь охлаждаются из-за ограничения скоростей движения. При установившейся температуре создается установившаяся скорость теплового потока в сторону плоскости сот.

Аналогично, тепловой поток, направленный в областях с бОльшим гравитационным градиентом вверх от плоскости сот, понижает температуру нагретых молекул воздуха, которые вновь нагреваются благодаря увеличению скоростей движения. При установившейся температуре создается установившаяся скорость теплового потока вверх от плоскости сот.

Очевидо, тепловой поток, направленный вверх из области с бОльшим гравитационным градиентом, на некоторой высоте переобразуется в тепловой поток, направленный вниз в соседнюю область с меньшим гравитационным градиентом. Таким образом, над плоскостью сот создается область с пульсирующим тепловым потоком (пчелы и сами поддерживают тепловой режим улья, но мы рассматриваем только соты).

На рис. 7 показан фрагмент пчелиных сот в прямоугольных координатах X, y, z. Тепловой поток над пчелиными сотами показан на рис. 8, где

• •    синим цветом показана функция распределения плотности масс P g (0,Q, z) по оси oz (из рис. 3; здесь мы для дальнейшего переименовали координаты);

• •    красным цветом показанаы линии теплового потока ,

• •    зеленым цветом показана функция мощности теплового потока Р.

Эту функцию можно аппроксимировать функцией вида

Р = P₀Sin ² ( ^) ,                  (12)

Л где Л - длина «волны» (обозначенная на рисунке как L). Эта функция не зависит от времени и не является волной в физическом смысле этого слова. В установившемся режиме при постоянной температуре эта функция определяет величину мощности теплового потока над точкой у и на определенной высоте z. Амплитуда Ро зависит от высоты z.

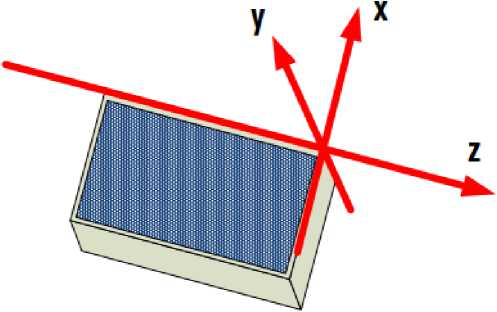
Рис. 7.

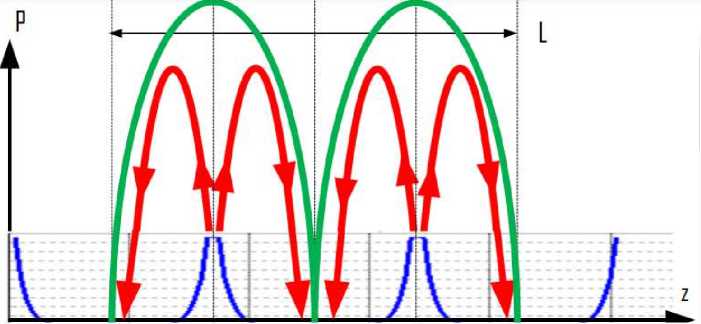
Рис. 8.

Вышесказанное относится к любым плоским полостным структурам, имеющим вид, показанный на рис. 7, - над ними создается область с тепловым потоком, который, как известно, является потоком энергии. Источником этой энергии является гравитационное поле Земли, создающее немонотонное статическое поле плоской полостной структуры (ППС).

Тепловой поток, как известно, - это предача энергии между движущимися молекулами и энергия, передаваемая в этом движении, — это кинетическая энергия молекул. Таким образом, в нашем случае мощность теплового потока

Р = F y V y ,                                 (13)

где

V y - скорость молекул воздуха в вертикальном направлении у , F y - сила, зависящая только от конструкции ППС и создаваемая гравитационным полем Земли.

8.    Движение ППС

Предположим, что ППС, над которой мощность теплового потока пульсирует по функции (12), движется со скоростью vz вдоль координаты z. Это эквивалентно тому, что этот тепловой поток движенся со скоростью vz(это следует из эффекта пограничного слоя Прандтля: вязкость воздуха приводит к тому, что пограничный слой воздуха прилипает к твердой границе и движется вместе с ней). При этом мощность теплового потока изменяется во времени - возникает бегущая волна теплового потока, которая описывается формулой вида

Р = Р _о sin ² ( ^t + 2^ ),

Л

где

Vy

Ы = f                                 (15)

Л

• - см., например, [12].

Далее будет показано, что воздушная бегущая волна теплового потока катализирует появление сил Кориолиса, которые увеличивают скорость движения этой бегущей волны. Эта волна (в следствии упомянутого эффекта пограничного слоя Прандтля) увлекает ППС. Таким образом, ППС ускоряется. Важно отметить, что энергию для этого ускорения доставляют силы Кориолиса, которые создаются гравитационной энергией Земли.

По существующим представлениям силы Кориолиса являются фиктивными силами и поэтому не могут совершать работу. В [15] обоснована реальность этих сил, выявлена физическая причина их появления и показано множество необъяснимых природных явлений и технических устройств, которые становятся объяснимыми на основе использования этих сил. Источником энергии для этих сил является гравитационная энергия Земли

Итак,

• 1.    над ППС создается статическое поле теплового потока, источником энергии для которого является гравитационная энергия Земли;

• 2.    если ППС начинает двигаться, то появляются силы Кориолиса.

• 3.    эти силы ускоряют движение ППС.

9.    Полет насекомых

Полет насекомых, крылья которых покрыты ППС, - это, по существу полет ППС. Это следует из многочисленных описаний и фотографий насекомых в книге [13]. Важно отметить, ППС не может начать полет самостоятельно: силы Кориолисв начинают действуют на ППС только при его движении. Поэтому насекомое должно начать полет только собственными силами или в падении (как это делает, например, майский жук). Надо полагать, что полет насекомых только за счет собственных сил был бы невозможен. Поэтому природа могла создать, например, шмеля в виде мохнатого шарика с полным пренебрежением к законам аэродинамики.

Интересно мнение биологов по этой проблеме. В книге Свидерского [17] сказано следующее.

«Некоторые насекомые даже несмотря на встречный ветер могут сохранять скорость своего перемещения отностельно земли постоянной» - стр. 34. «Следует считать эффективность работы летательного аппарата насекомых исключительно высокой по сравнению с другими летающими животными (за исключением , пожалуй, лишьптицы колибри)» - стр. 36.

«Крыло насекомого как бы нарочно создано «антиаэродинамическим»! Вспомним его строение: оно покрыто раличными волосками, чешуйками, гребешками и другими образованиями … имеется и масса структур, не несущих рецепторной функции. Для какой же цели они существуют?» - стр. 40. Далее автор обсуждает предположение о том, что эти образования

Доклады независимых авторов 2024 выпуск 59 являются «турболизаторами», создающими микровихри, которые способствую ламинарному обтеканию крыла. Однако это не удается подтвердить.

Исследования последних лет показали, что сравнение движений крыла насекомого во время его работы с движениями весла весьма мало напоминает реальную ситуацию, а название машущего полете «гребной», как это было принято еще сравнительно недавно в учебниках энтомологии, неправильно. И если уж с чем-то сравнивать, то скорее можно провести аналогию с работой пропеллера самолета. Да и в этом случае общего не так уж много.» -стр. 41.

«К сожалению, теории машущего полета насекомых еще нет и вряд ли из-за многочисленных трудностей такая теория в ближайшие годы будет создана» - стр. 47.

Таким образом, крылья насекомых могут рассматриваться как полостные структуры, привлекающие подъемные и движущие силы за счет движений, катализирущих появление этих сил .

10.    Математическая модель полета ППС

Будем рассматривать математическую модель в системе прямоугольных координат X, у, z, показанных на рис. 7. В [14, глава 5] показано, что для абсолютно замкнутых систем уравнения гидрродинамики принимают вид

^^ Av + р ■ F = 0,

где лагранжиан Av в прямоугольных координатах определяется формулой вида

’ F2vx , dx2	d2vx , dy2	d2vx ~
		dz2
d2V y y dx2	d^y , dy2	d2V y
		dz2
d2vz , - dx2 +	d2Vz , dy2	d2V z
		dz2 -

.

^{A v}xl A v = toy =

I ^Av z

Будем полагать (как указано в разделе 8), что воздух движется со скоростью v_z . При этом возникают массовые силы Кориолиса, создаваемые вращением Земли с угловой скоростью й о . Они определяются как

^Fx   ^2p ^ o^vz ,

Fz   2р^о^х, где р - плотность воздуха. Для средних широт шо ~ 10 5. Массовая сила Fy, создаваемая мощностью теплового потока P определим по

(7.13):

_    р Fy = 7/                                         (5)

Запишем уравнение (1) с учетом (2-5):

Г 2W o V z P"| р- Av +    Fy   =0.                        (6) [ 2^ o V x p]

При этом наша задача принимает вид системы трех уравнений с тремя неизвестными vx, Vy, Vz:

р- A V x + 2pV z ^ o = 0,	(7)
р - A V y + F y = 0,	(8)
р - A vz + 2pvxMo = 0.	(9)
Далее будем искать решение в следующем виде:
V x = bx si ,	(10)
V y = b y si ,	(11)
vz = bz si,	(12)
si = sin( fix + ay + xz) ,	(13)
где b, a, fi, x — некоторые константы. Подставляя (10-13) в (6), дифференцирования получаем: Г Avx]     \bx si-yl l A v y l = |b y sm A vzJ   Ib z si-yJ	после
	(15)
где
Y = fi2+a2+x2.	(16)
Подставляя .(10-12, 15) в (7-9), получаем
bxsrY + 2qbzMosi = 0,	(17)
b y sty + F y = 0 ,	(18)
bzsrY + 2qbxwosi = 0,	(19)
где
q = - . M	(20)
Одним из решений системы уравнений (17, 19) может быть:
b x = 2q^ o/ Y,	(22)
b x = b z .	(21)
Из (3, 4, 10, 12, 21, 22) получаем:
V x = V z = (2q^ o /Y)si ,	(24)
F x = F z = (2p^ o )2si/Y.	(25)

Определим еще плотности потоков энергии, циркулирующих вдоль осей координат:

S_x = F_xv_x, S_y = P = F_yv_y, S_z = F_z v_z .            (26)

Из (24-26) получаем:

S x = S z = (2pw₀)³si^2/y².                          (27)

Итак, способ полета состоит в следующем.

• 1.    Над неподвижным ППС существует статическое поле теплового потока (источником энергии для него является гравитационная энергия Земли); в этом поле есть скорость воздуха V y .

• 2.    Если ППС начинает двигаться со скоростью V_z , то возникает поток воздуха, в котором появляется также скорость V_x ; все скорости принимают единую форму вида (10-12).

• 3.    Вслед за появлением скоростей появляются силы Кориолиса (3, 4) (источником энергии для которых является гравитационная энергия Земли).

• 4.    При появлении этих сил движение воздуха ускоряется; через некоторое время ускорение прекращается из-за внутреннего трения в воздухе.

• 5.    Установившиеся скорости существенно превышают начальные значения; вместе со скоростями создаются потоки механической энегии воздуха, которые увлекают ППС (благодаря существованию эффекта пограничного слоя Прандтля)

В установившемся режиме сила F y равна весу ППС. При этом из (11, 18) может быть найдена амплитуда скорости V y :

F, vy = 7                                (28)

Амплитуды скоростей V_x = V_z найдем из (24):

V x = V z = 2q^ 0 ^/ Y ,                              (29)

Из (24, 29) следует, вектор суммарной скорости ППС в горизонтальной плоскости повернут на угол я/4 относительно вектора начальной скорости v _Z0 , с которой началось движение ППС. Амплитудв суммарной скорости

V xz = V z V2.                                        (30)

Амплитуды сил F_x = F_z найдем из (25):

F xo = F zo = (гр^ о)²^ .                         (31)

Амплитуды мощностей S_x = S_z найдем из (27):

$ х о = ^ zo = (2pwo)3/y 2 .	(32)
Будем полагать, что в горизонтальной плоскости скорость V xz = U xz sin( ut + zz) или	(33)
2n . vyZ = Vxz Sin( Mt + — z),	(34)
где длина этой волны Л =^ . X Известно (см., например, [12]), что скорость волны определяется V = uL	(35) как (36)

В нашем случае амплитуда волновой функции являтся скоросттью ее движения, следовательно,

Ы = ^р                                (37)

Л

Мы нашли характеристики волны воздуха, которая движет ППС.