Полетная параметрическая идентификация и силовая гироскопическая стабилизация крупногабаритного спутника

Используя опыт исследований и проектирования [1-3] гиросиловых систем управления движением упругих космических аппаратов (КА), рассматриваются задачи идентификации и стабилизации крупногабаритных информационных спутников – космической связи (апертура антенн до 25 м), радиолокации (апертура до 500 м) и др. При этом используется плодотворный подход Б.В. Раушенбаха и Е.Н. Токаря (1975), основанный на совместной и согласованной разработке как КА с крупногабаритной конструкцией, так и его системы управления ориентацией (СУО). Только при таком рационально-интегрированном подходе удается выполнить противоречивые требования к жесткостным и габаритно-массовым, маневренным и точностным характеристикам КА при ограниченности его бортовых энергетических и вычислительных ресурсов с обеспечением необходимого уровня надежности СУО.

вым гироскопическим комплексом (СГК), где составляющие его шесть гиродинов (ГД) имеют редукторные приводы по осям их подвеса.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Стандартным образом вводятся инерциальная (ИСК), связанная (ССК) и орбитальная (ОСК) системы координат (СК). Состояние ССК относительно ИСК определяется кватернионом Д , относительно ОСК - вектором-столбцом Ф = { ф , , ф ₂ , ф ₃} , составленном из углов рыскания, крена и тангажа, а также вектором абсолютной угловой скорости to . Динамика существенно упругого КА с СГК представляется векторно-матричным соотношением

m 13 [-Lx] M q " Г *1 v Г Fv" [Lx] J D q to = F » ,    (1) m q D ‘ q Aq . *i. _F q _ где m – суммарная масса КА и векторы-столбцы

F ^v = - m ( ш х v ) + ш х ( L х щ - 2 L ) - R _w у - r g ( у , у , to ) + R _c ;

P = u g;

F " = - L x ( го х v ) - A _H( P ) p - to x G - J w Y - m _g ( у , у , to ) + M 0

F q =- A q ( V q q + W q q ) - M q ( to x v ) - P W у ^.

Здесь при обозначениях [•] - строка, {•} -столбец, (•)* - символ транспонирования, [ax] -косо-симметричная трехмерная матрица на основе вектора a, имеем q = {q p, qa}, qp = {q,p, q 2p} и qa - векторы-столбцы упругих перемещений панелей СБ и антенн, соответственно; Mq = Mq(у) = [Ap(у),Aa] - матрица взаимовлияния поступательного движения КА с двумя панелями СБ и антеннами, где A p(Y) = [A pi(Y), A p2 ( Y)l; Dq = [B p( Y), Bal — матрица взаимовлияния вращательного движения КА с двумя панелями СБ и антеннами, где Bp(Y) = [Bpi(Y),Bp2(Y)]; Aq = I — матрицаобоб-щенных масс, нормированная к единичной матрице; Vq = diag{(5p/ ^)Qpi,(5p/ n)Qp„(5a/ ^)Q a} — матрица конструктивного демпфирования; Wq = dlag{(QpJ2,(Qp,)2,(Qa)2} — нормированная матрица жесткости; RJPw - векторы-столбцы, отражающие инерционное влияние поворотного перемещения панелей СБ, как твердых тел, относительно корпуса КА; rg (Y, Y, to) и mg (Y, Y, to) – нелинейные векторные функции, отражающие гироскопическое влияние перемещений панелей СБ на угол Y относительно корпуса КА; K = K(y, to) = J(Y) to - вектор кинетического момента (КМ) КА, как системы твердых тел; l = m q q – вектор статического момента КА, как упругой конструкции; Rc и Mo – суммарный вектор внешних сил негравитационной природы, прилагаемый в центре масс (ЦМ) С, и суммарный внешних моментов относительно полюса О, соответственно; вектор-столбец P = {Pp } составлен из углов поворота гиродинов, вектор G = D q (Y )q + K (Y, to) + H(P) представляет КМ упругого КА вместе с СГК, вектор H(P) = hg h(p) – суммарный КМ СГК на основе шести ГД с одинаковым КМ h , матрица A H(P) = hg Ah (P) = hgdh / dp , а управлением считается вектор p = ug скоростей прецессии ГД с формированием кусочно-непрерывного гироскопического управляющего моментаMg = —Ah(P) ug. передаваемого СГК на корпус КА.

При выборе схемы расположения гиродинов в ССК учитываются требования, предъявляемые к гиросиловой СУО КА. При наличии трех пар ГД все внутренние сингулярные состояния СГК

строго проходимы , здесь рациональна каноническая схема 3-SPE (система 3 ножничных пар – 3 Scissored Pair Ensemble), состоящая из трех ортогонально ориентированных пар ГД, рис. 1. Введем вектор-столбец P = { P _p , p = 1 ^ 6} , составленный углов ГД относительно осей их подвеса, см. рис.1. Парковое состояние СГК данной схемы, когда вектор нормированного суммарного КМ СГК h ( P ) = X h _p ( P _p ) = 0 , представлено на рис. 2. Введем обозначения проекций ортов КМ каждого ГД на оси ортогонального канонического гироскопического базиса (КГБ) G- g g „gl .

c ^{ x c , y c , z c ^} :

x ₁ = C ₁ = cos P ₁ ;

У 1 = 5 1 = ^s in ^P 1 ; x ₃ = 5 ₃ = sin P ₃ ; z ₃ = C ₃ = cos P ₃ ;

У 5 = ^C 5 = ^{cOs P} 5 ; z 5 = 5 5 = sin P 5 ;

x ₂ = C ₂ = cos P ₂ ; y 2 = 5 2 = sin P 2 ; x ₄ = 5 ₄ = sin P ₄ ; z ₄ = C ₄ = cos P ₄ ; У 6 = ^C 6 = ^{cos P} 6 ; z 6 = ⁵ 6 = ^{sin P} 6 .

Тогда вектор-столбец нормированного суммарного КМ СГК h в гироскопическом базисе G c и градиентная матрица A h ( P ) = d h / d P представляются в виде

h =

x

y

z

^{- 5} 1 A h ( P ) = C

C ₁ + C ₂ + 5 ₃ + 5 ₄ 5 1 + 5 2 + C ₅ + C 6

C 3 + C 4 + 5 ₅ + 5 6

- 5 ₂ C 2 0

C 3

C 4 0

-

-

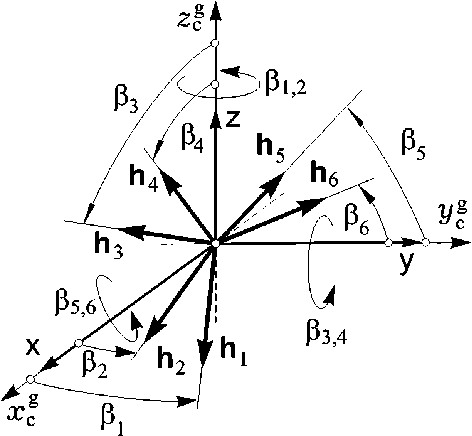
Рис. 1. Кратная схема 3-SPE

-

C 5

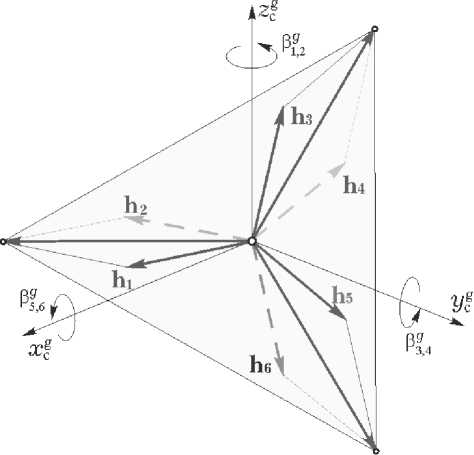
Рис. 2. Парковое состояние СГК

Сингулярные состояния этой схемы возникает при таких угловых положениях ГД, когда матрица Грамма G ( P ) = A h ( P ) A h (| 3 ) теряет полный ранг, т.е. при G = det( G ( P )) = 0 . Принципиальной проблемой управления СГК избыточной структуры является выбор функции распределения потребного суммарного КМ СГК между ГД – закона настройки СГК.

ПОСТАНОВКА ЗАДАЧИ

Предполагается применение авторского подхода к обработке сигналов в бесплаформенных инерциальных навигационных системах (БИНС) с астрономической коррекцией [4]. Такие БИНС содержат инерциальный блок в виде гироскопических измерителей приращений квазикоординат углового положения КА и астрономическую систему на основе звездных датчиков с широким полем зрения, закрепленных на корпусе КА. В результате такой специализированной обработки с численным интегрированием кинематических уравнений по информации только о векторе дискретных приращений квазикоординат, получаемого ИБ при наличии шумов, с калибровкой (идентификацией и компенсацией дрейфа ИБ и вариации масштабного коэффициента измерения вектора угловой скорости to ) и юстировкой (идентификацией и компенсацией погрешности взаимной угловой установки систем координат ИБ и АС) формируются оценка to (t) вектора to (t) и оценка Л(t) кватерниона Л(t) ориентации спутника в ИСК с заданным периодом измерения Tq , который выбирается кратным периоду Tu цифрового управления СГК, причем Tu > Tq.

В наземных условиях весьма затруднительно выполнить экспериментальное определение даже низших парциальных частот Q , = 2 л f_s^й ( fs ^Q ~ 0.01 Гц) упругих колебаний крупногабаритной конструкции КА в модели (1), которым соответствуют собственные частоты колебаний to _s = 2 л f ” > Q _s этой конструкции в составе КА. Поэтому на этапе летно-конструкторских испытаний и далее при штатной эксплуатации КА с длительным сроком активного существо-

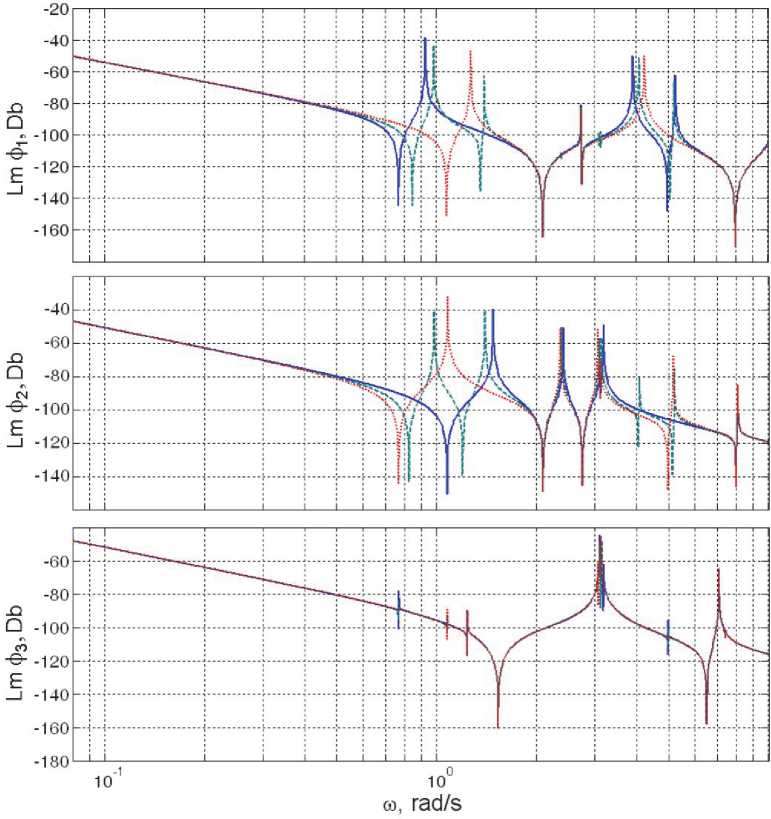
Рис. 3. ЛАЧХ спутника по каналам при различных углах Y с шагом 45 ° по каналам рыскания (синий цвет), крена (зеленый цвет) и тангажа (красный цвет)

вания (до 15 лет) необходима идентификация инерционно-жесткостных параметров крупногабаритной конструкции спутника.

Предполагается получение дискретных сигналов БИНС с периодом T q (кватернион Л ₅ , 5 Е N ₀ = [0,1,2,...) , вектор угловой скорости to ₅ ) и дискретных измерений вектора H ₅ КМ СГК в связанном базисе. Полученная при этом информация эпизодически (в том числе после разгрузки СГК либо коррекции орбиты КА) используется для адаптивной настройки алгоритмов дискретной фильтрации выходных сигналов БИНС и цифрового управления СГК. Задача состоит в разработке методики полетной идентификации низших резонансных частот и тензора инерции крупногабаритной конструкции КА, построении законов настройки СГК, а также в синтезе алгоритмов дискретной фильтрации доступных измерений с периодом T q и цифрового управления СГК с периодом T u . При этом предполагается, что высота полета КА составляет не менее 550 км, где проявляется малое влияние внешних возмущающих моментов и медленное изменение накопленного вектора КМ СГК, а также что гиросиловая СУО сбалансирована по вектору суммарного КМ – при отсутствии накопленного КМ и парковом состоянии СГК ( H = 0 ) равенство G = 0 обеспечивается при условии K = 0 .

ПОЛЕТНАЯ ИДЕНТИФИКАЦИЯ СОБСТВЕННЫХ ЧАСТОТ КОЛЕБАНИЙ КОНСТРУКЦИИ

Чтобы оценить сложнейшую проблему управления КА с упругой слабо демпфированной конструкцией, в качестве примера на рис. 3 представлены логарифмические амплитудные частотные характеристики (ЛАЧХ) спутника по каналам при фиксированных положениях панелей СБ, определяемых углом уЕ [-90 ° , + 90 ° ] с шагом 45 ° . Нетрудно убедиться, что здесь низшие резонансные частоты колебаний упругой конструкции в каналах рыскания ( ф 1 ) и крена ( ф ₂ ) существенно мигрируют в зависимости от угла У , а в канале тангажа ( ф ₃ ) такая зависимость весьма незначительна. Ясно, что с увеличением частоты входного сигнала колебательные свойства упругой конструкции спутника проявляются очень существенно и для повышения точности в каждом канале не позволяют увеличить позиционные коэффициенты при любом линейном законе управления из-за очевидно возникающей потери устойчивости.

Совокупность дискретных значений векторной функции to(tp) с назначаемым периодом Tp на “базисном” временном интервале Tb приводит к трехмерному массиву значений вектора угловой скорости корпуса КА по трем каналам его угловой стабилизации. Последующая обработка этого массива экспериментальных данных с помощью алгоритма быстрого преобразования Фурье [5] непосредственно в комплексных числах приводит к искомым оценкам (О5 набора низших резонансных частот to5 крупногабаритной конструкции КА. С помощью функции fft программной системы Matlab предлагаемая методика была апробирована [6] на модельной задаче для геостационарного КА с крупногабаритной конструкцией, три произвольные низшие парциальные частоты которой принадлежат отрезку [0.01 0.05] Гц. При Tp = Tu = 4 с и Tb = 7200 с соответствующие три резонансных частоты были идентифицированы с точностью 0.5 %.

ПОЛЕТНАЯ ИДЕНТИФИКАЦИЯ ТЕНЗОРА ИНЕРЦИИ

Идентификация тензора инерции J выполняется при пассивном орбитальном движении центра масс КА ( R _c = 0 ) в общем случае в 2 этапа с использованием указанных бортовых дискретных измерений на основе обобщенного интеграла для вектора суммарного КМ механической системы КА+СГК в ССК , который представляется в виде

G ( t ) = K ( t ) + H ( t ) = Л ( t ) ° [ Л ( t ₀) ° G ( t ₀) ° Л ( t ₀) +

+ I" Л ( r ) ° M o ( r ) ° Л ( т )d r ] ° Л ( t )                 ⁽²⁾

1 o

На 1 этапе пренебрегается влиянием неиз- вестного внешнего возмущающего момента, за- висящего от неизвестного значения тензора инерции КА J , т.е. полагается M o (t) = 0.В этом случае вектор КМ механической системы неизменен в ССК, т.е. G1 ( t) = GO = const, где

G | ( t ) = Л ( t ) ° G ( t ) ° Л ( t ) , G O = Л ( t o ) ° G o ° Л ( t o ) и

G o = G ( t o ) = K ( t o ) + H ( t o ) .

Вектор K(t) = Jto (t) КМ корпуса КА в про- извольный момент времени t зависит от неиз- вестного значения тензора инерции J , поэтому в условиях сбалансированности СУО по кинетическому моменту вектор накопленного КМ G o однозначно определяется только при условии to (t ) = to = 0 , в результате получается Go = Ho = H( to).

Для идентификации неизвестного значения тензора инерции КА J на некотором интервале времени t Е T = [to, tf] выполняется программное пространственное угловое движение КА с выделением 5 сегментов длительностью Ta с гладко-сопряженными переходами между ними (для слабого возбуждения колебаний конструкции КА), где последовательно выполняются:

(o) стабилизация корпуса КА в ИСК с вектором угловой скорости to = to o = 0 ;

(a), (b) и (c) – стабилизация корпуса КА в ИСК с постоянными векторами угловой скорости to = to । , i = a,b, c , причем направления векторов to _a , to _b и to _c должны быть линейно независимы;

(f) – стабилизация корпуса КА в ИСК с вектором угловой скорости to = to _f = 0 .

Далее выполняется цифровая обработка выходных дискретных сигналов БИНС ( Л _s , to _s ) и измерений H s вектора КМ СГК с помощью дискретных фильтров полиномиального сглаживания Савицкого – Голея, что дает точную оценку этих переменных в функции времени t E [ t _o, t _f] . Затем по определенному алгоритму выбираются моменты времени t i* , i = o,a,b, С и f , для которых вычисляются оценки Л ( t i* ) , to ( t i* ) и H ( t i* ) . Для индексов i = a,b, С вектор K ( t i* ) = J to ( t i* ) КМ корпуса КА с неизвестной симметричной матрицей инерции J = || J || = || J i II, г , ^j = 1,2,3 представляется в виде K ( t i* ) = Q ( to ( t i* )) I , где вектор-столбец I = { 1 1 , 1 2 , I з , 1 ₄, 1 ₅, 1 ₆} = { J ii , J 22 , J 33 , J 12 , J 23 , J 13 ,} и прямоугольная 3х6-матрица Q ( to ( t i* )) имеет очевидную структуру, и вычисляется оценка G ' ( t _o * ) = Л ( t _o * ) ° H ( t _o * ) ° Л ( t _o * ) значения вектора накопленного КМ в инерциальном базисе при условии to ( t _o * ) = 0 . С этой целью составляется система уравнений

Q(to(t*)) I = -H(t,*) + Л(t,*)°GI(10*)°Л(t„), i = a,b, c относительно компонентов вектора-столбца I , которая численно разрешается по методу наименьших квадратов с получением оценки I и, следовательно, искомой оценки J тензора инерции. Наконец, на основе сопоставления оценок G1 (to*) и GI(tf*) вектора накопленного КМ в ИСК при оценках to, Л, H и J для моментов времени to* и tf * определяется необходимость выполнения 2 этапа идентификации тензора инерции.

На 2 этапе учитывается влияние малого неизвестного внешнего возмущающего момента, зависящего от неизвестного значения тензора инерции J . При этом вектор G ¹ ( t ) ^ Л ( t ) ° G ( t ) ° Л ( t ) изменяется в ИСК в соответствии с векторным уравнением d G ¹ ( t ) / dt = M 0 ( t ) = Л ( t ) ° M ₀ ( t ) ° Л ( t ) , где неизвестный вектор внешнего возмущающего момента M 0 ( t ) в инерциальном базисе принимается кусочно-постоянным, т.е. в дополнении к обобщенному векторному интегралу для вектора КМ механической системы производится расширение модели с помощью векторного уравнения d M 0 ( t )/ dt = 0 V t E T m = [ t k , t k _{+ 1}) C T .

При измерениях to _s , Л _s , H _s , фильтрации этих измерений по методу Савицкого – Голея и

последующем вычислении значений G I ( t k ) строится дискретный идентификатор Луенбергера для получения оценки M 'o ( t ) = const V t e [ t k , t k ₊ 1 ). При этом задача решается итерационно с применением полной формы представления обобщенного интеграла (2) для вектора суммарного КМ механической системы КА+СГК, а за начальное значение искомого тензора инерции принимается оценка J , полученная на первом этапе идентификации.

Разработанная методика полетной идентификации тензора инерции КА была апробирована на основе компьютерной имитации при следующих параметрах: длительности временных интервалов T = 360 с, T q = 0.25 с, T a = 30 с, T m = 4 с; векторы угловой скорости to a , to b и to _С с модулем 0.5 град/сек расположены равномерно на поверхности кругового конуса с углом полу-раствора 10 ° ; погрешности БИНС и ошибки измерения вектора КМ СГК соответствуют технически реализуемым в настоящее время. В результате численных расчетов было установлено, что любой компонент тензора инерции восстанавливается: с точностью 0.1% при отсутствии накопленного КМ и внешнего возмущающего момента, с точностью = 0.2% при отсутствии внешнего возмущающего момента и с точностью = 0.5% при наличии малого внешнего возмущающего момента, которая достигается за 25 итераций.

ЯВНЫЙ ВЕКТОРНЫЙ ЗАКОН НАСТРОЙКИ СГК

Наиболее рациональными являются явные законы настройки ГД, при которых все характеристики движения каждого ГД получаются по аналитическим соотношениям. Вводятся обозначения

x ₁₂ = x 1 + x ₂ ;

x ₃₄ = x ₃ + x ₄ ;

у 12 = у 1 ⁺ у 2 ;

у 56 = у 5 ⁺ у 6 ;

z 34    z 3 ⁺ z 4 ^;

z 56    z 5 ⁺ z 6 ^;

~ x12 =

У 12

z 34 ⁼

x 12

У 12

2 x 12

z 34

~

; x 34

x 34

2 ; z 34

;

У 56

У 56

2 ; z 56

;

² x 34

z 56 ⁼

z 56

и компоненты явного векторного закона настройки f . ( P ) = { / ,„ f , 2 , f , 3 } ■ 0 СГК схемы 3-SPE принимаются в виде

fx ( P ) = / „ ( P ) = X 12 - X 34 + P (. ^ 12 X 34 - 1) ;

X ( P ) = f x 2 ( P ) - ~ 56 - ~ „ +P (~ ,₆ y „ - 1) ; (3) f „ ( P ) = f x 3 ( P ) » ~ 34 - ~ 56 +P (~ '56 - 1) , где постоянный параметр р удовлетворяет условию 0 < р <  1 . Данный закон настройки обеспечивает отсутствие сингулярных состояний СГК для всех внутренних точек области вариации вектора его суммарного КМ. Для представления условий однозначной разрешимости уравнения h ( P ( t )) = h ( t ) , где h ( t ) = { x ( t ), y ( t ), z ( t )} является известной векторной функцией, относительно синусов и косинусов углов P p ( t ) всех гироди-нов, вводятся обозначения

Р 12 = 7^{4 - ( x} 12 ^{) 2} ; ^ 12 = 7^{4 - (} у 12 ^{) 2} ;

числение синусов и косинусов углов P _p ( t ) всех шести гиродинов выполняется по явным аналитическим соотношениям

_ X + Ax , У-Ay         I 2 ,2

a 1        2 ^{; b}1       2 ^; c ¹ = 7 a ^{1 +} b ^{1 ;}

z+A X-A d 1 = 74 - c / c; a2 =       ; b2 =

c 2 = 7 a 2 + b 2 ^; d 2 = 7 ⁴ - c 2 / c 2 ^; a 3

У + A y

2 ;

^b 3       2 ^; c 3 = 7 a ² + b ₃ 2 ^; d 3 = 7⁴ - c ² / c 3 ^;

1-я пара (ГД1 и ГД2):

p 34    Т^{4  ( 2} 34 ) ; q 34    Т^{4  ( Х} 34 ) ;

p 56 = 7^{4 - (} у 56 ^{) 2} ; q 56 = 7^{4 - ( 2} 56 ^{) 2} ;

X + Ar X12 =

¹² 2

У + A y ^x 56 = ₂

2 = ^ ^ 34 2

;

;

^Х 3 4

У 12 =

² 56 =

X -A X

y - A

;

y

;

z -A ____________ z .

2 ;

a 1 ^- d 1 b 1          b 1 ⁺ d 1 a 1

^x 1 =             ; ^y 1 =

a 1 + d 1 b 1	b 1	- d 1 a 1
x 2        2 ;	y 2	2 ;
2-я пара (ГД3 и	ГД4):
b 2 + d 2 a 2	a 2	- d 2 b 2
3           2 ;		2

b ₂ - d ₂ a ₂         a ₂ + d ₂ b ₂

^x 4 = —n—; ² 4 = —й—

3-я пара (ГД5 и ГД6):

d x = q ^ ⁺ p 34 ;

d y = q 56 ⁺ p 12 ;

d , = q 34 ⁺ p 56 •

Условия разрешимости векторного уравнения h ( P ( t )) = h ( t ) имеют вид

A x = d x {1 - [1 - 4 р (( q 12 - p 3 ₄)( x /2) +

+ P ( q 12 p 34 - ( X /2)²))/ d ²]^1/2}/ р       ^;

A y = d y {1 - [1 - 4 р (( q 56 - p ₁₂)( y /2) +

+ P ( q 56 p 12 - ( У /2)²))/ d ²]¹ / ²}/ P

• A , = d , {1 - [1 - 4 p (( q 34 - p 56 )( z /2) +

+ P(q34p56 -(z/2)2))/d2]1/2}/р и при введении вектора-столбца A(t) = {Ax (t), Ay (t), A, (t)} очевидным образом преобразуются к нелинейному векторному уравнению A (t) = Ф(h( t), A (t)) . Получить аналитическое решение этого векторного уравнения весьма затруднительно, но его численное решение достигается практически мгновенно по методу простой итерации – при рациональном выборе начального точки итерационного цикла достаточно лишь 1-2 итерации для получения результата с приемлемой точностью. Далее вы-

• a. - db     b + da

y =        3_^ . 2 =   ³—A .

• 5 2 ; 52

• a. + db    b - da

У a = — 3-A" • 2 c. =   x 6         2 ; 62

ФОРМИРОВАНИЕ

УПРАВЛЕНИЯ ГИРОДИНАМИ

Алгоритмы управления ГД в составе СГК приводятся в нормировке к постоянной величине h g собственного КМ каждого из шести гиро-динов. Управляющий гироскопический момент СГК M g = - A _H ( P ) u g представляется в виде M g = - A h ( P ) u g = - h g A h ( P ) u g = h g m g , где [3 = u ^g и вектор-столбец m ^g = - A h ( P ) u ^g = - A h ( P ) P соответствует нормированному моменту СГК. Пусть состояние СГК (вектор-столбец P g R ⁶ ) известно и задан вектор-столбец m ^g g R ³ потребного нормированного момента СГК. Тогда при использовании явного закона настройки ^f x ^{( P )} = ^{ f X 1 , f x 2 , f x 3^} = ⁰ СГК (2) возможно абсолютно точное и однозначное определение вектора-столбца u ^g = P g R ⁶ командных скоростей прецессии каждого из 6 гиродинов в составе СГК на основе шести скалярных уравнений, представленных в виде

Ah(P)P=-mg; (P,9f„(P)/3P) = 0, s = 1 ^3.

Аналитическое решение уравнений дается соотношением u g ( 0 , m g ) = 0 = D ( 0 ){ — m g , 0 } ; D ( P ) = ( A ( 0 )) 1 , где основная задача состоит в аналитическом обращении матрицы

A ( P ) =		" A h ( P ) " d f , 1 ( P )/ Э 0 Э f p 2 ( P )/ Э 0 Э f p 3 ( P )/ э р		=
	— У 1	— У 2	z 3	z 4	0	0 ■
	x 1	x 2	0	0	— Z 5	— Z .
=	0	0	— X 3	— X 4	y 5	У 6
	a 41	~ a 42	~ a 43	a 44	0	0
	~ 51	~ a 52	0	0	~ a 55	a 56
	_ 0	0	~ a 63	a 64	~ a 65	a 66 J

с учетом 6 тождеств

22  22  22  22

X 1 + У 1 — 1 ; X 2 + y 2 — 1 ; x 3 ⁺ z 3 — 1 ; X 4 + Z 4 — 1 ;

у 2 ^{+ Z} 5 ^{— 1} ; у 62 ⁺ z б ^{— 1} .

При обозначениях s12 = q12 — PX 12 ; s34 = q34 — PZ34 ;

s56 = q56 — Py56 ; v 12 = p12 + Py 12 ’ v34 = P34 + PX34 ; v56 = P56 + PZ56 ';

r12 = 1 + У1У2 + X1 X2 ;   r34 = 1 + Z3Z4 + X3 X4 - r56 = 1 + Z5 Z6 + У5 У6

получаются соотношения для всех неочевидных ~ элементов матрицы A(P):

a 41

^— v 34

⁴ У 1 ^{— r} 12 У 12 . p ₃₄ ( q ₁₂ ) ³

a 42

⁴ У 2 ^{— r} 12 У 12 p ₃₄ ( q ₁₂ ) ³

~ a ₄₃

—

s ₁₂

^{4 Z} 3 ^— r 34 ^Z 34 . q 12 ( p 34 ) ³

~ a ₄₄

^{4 Z} 4 ^— r 34 ^Z 34 . q 12 ( p 34 ) ³

~ a 51 = s 56

L x 1 ^— r 12 x 12 . q ₅₆ ( p ₁₂ ) ³

~ a52 =

^— s 56

Г ^x 2 ^— r 12 ^x 12 . q ₅₆ ( p ₁₂ ) ³

~ a55 =

^{4 Z} 5 ^— r 56 ^Z 56 p 12 ( q 56 ) ³

~ a56 =

^— v 12

^{4 Z} 6 ^— r 56 ^Z 56 p 12 ( q 56 ) ³

~ a63 =

^— v 56

I x ₃ — r ₃₄ X ₃₄ . p ₅₆ ( q ₃₄ ) ³

~ a 64 = v 56

' 4    r 34 ^X 34

p ₅₆ ( q ₃₄ ) ³

~

a 5 ⁼

^— s 34

⁴ У 5 ^— r 56 У 56 q 34 ( p 56 ) ³

~

a =

^— s 34

⁴ У 6 ^{— r} 56 У 56 q 34 ( p 56 ) ³

Аналитический вид матрицы 1 ~( 0 ) здесь не приводится из-за его громоздкости.

АЛГОРИТМЫ ДИСКРЕТНОЙ ФИЛЬТРАЦИИ И ЦИФРОВОЙ ГИРОСКОПИЧЕСКОЙ СТАБИЛИЗАЦИИ

Изучение собственных свойств линейной модели механического объекта, дискретизиро-

ванного с периодом управления T u , является важным этапом синтеза цифрового закона гиро-силовой стабилизации спутника. Выбор периода дискретности при формировании управления в этом случае имеет ряд особенностей, главным из которых является весьма коварное свойство транспонирования частот. Суть этого явления заключается в возникновении эффекта типа “биения”, когда резонансная частота какого-либо тона упругих колебаний конструкции КА располагается в малой окрестности частот, кратных удвоенной частоте Котельникова-Шеннона, т.е. кратных круговой частоте Ш ₂ ksh = 2 л / T u . При наличии такой ситуации, в полном соответствии с теорией дискретных систем с фиксированным периодом, появляется низкочастотный обертон (огибающая “биения”), частота которого может переместиться (транспонироваться) в область частоты среза ЛАХ в каком-либо канале стабилизации. При выборе периода дискретизации учитываются также собственные фильтрующие свойства фиксатора (экстраполятора нулевого порядка) – основного элемента цифрового управления. Для рассматриваемого механического объекта период дискретности управления был принят в виде T u = 4 c. Сопоставление частотных свойств непрерывной и дискретной модели КА со слабо демпфированной конструкцией наиболее просто выполнять в низкочастотной области, вплоть до круговой частоты 2 / T u = 0.5 рад/с, где круговая частота близка к абсолютной псевдочастоте X , to = X . В этой частотной области ЛАХ непрерывной и дискретной моделей практически совпадают, но имеются принципиальное отличие в поведении ЛФХ дискретной модели - ЛФХ принимает значение, меньшее — л . При расчете дискретных частотных характеристик наиболее “тонким” вопросом является эффективный расчет матричной экспоненты и интеграла от нее. Анализ свойств дискретной модели для всех расчетных положений (угла Y ) панелей СБ позволяет сделать принципиально важное заключение – для обеспечения устойчивости и необходимого качества системы стабилиза-

ции упругого спутника определяющими являются только 1-2 низших тона упругих колебаний панелей и антенн.

Для управления ориентацией используется

измерение только углового положения корпуса КА в моменты времени t s = s T q , s G N₀ , с периодом T_q <  T u , кратным периоду управления T u . Дискретизация с периодом T q непрерывного апериодического звена с передаточной фун-

кцией W (s) = 1/(1 + T f s) и постоянной времени T f , без фиксатора на входе для каждого ка-

нала управления при введении нормировки приводит к дискретной передаточной функции

W _f(z_q) = (1 + b f )/(1 + b f z q ¹) ; b f exp, - T q / T J ; Z q = exp(s T q ) с условием W _f(1) = 1 .

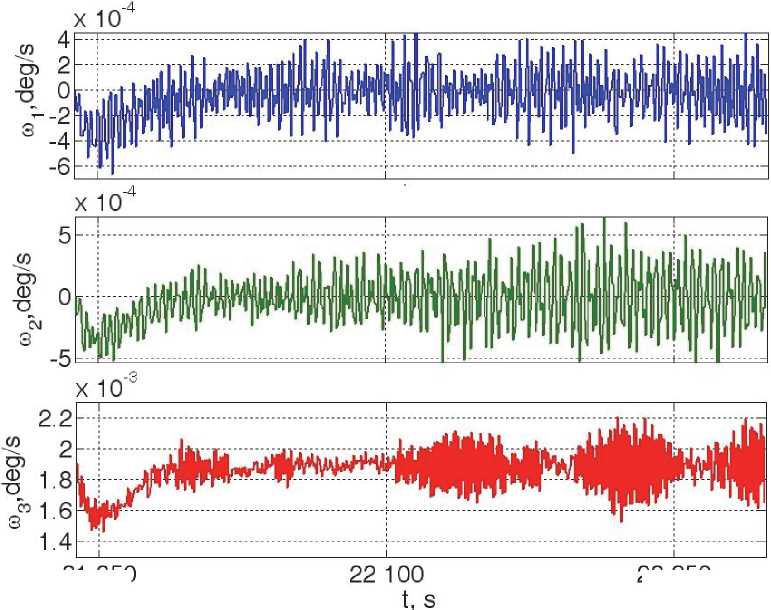
Применение такой фильтрации в каждом канале соответствует алгоритму дискретной фильтрации ys +! =-b1;vs + (1 + b!f)Es +!, где £s = фS — фs является рассогласованием дискретной команды фс по углу ориентации корпуса КА и дискретного сигнала ф измеряемого углового положения КА. При параметрах p = (1 — b )/(1 — a ) и С = p (b — a ) , где a = [( 2 / T„ )T1 — 1]/[(2/Tu )t; + 1] и b = [(2/Tu)x2 —1]/[(2/Tu)x2 + 1], разработанный дискретный алгоритм управления в каждом канале с формированием с периодом Tu цифрового компонента mk вектора стабилизирующего ускорения имеет весьма простой вид:; gk+1 = bgk+ cek; mk = k(gk+ p£k), где координата gk является дискретной “рабочей” переменной. В итоге в каждом канале гиросиловой стабилизации КА имеется два периода дискретизации [2], поэтому здесь встают проблемы агрегирования и анализа устойчивости линейной непрерывнодискретной системы многократного типа, в общем случае с физическим временным запаздыванием. Решение этих проблем получено в работе [2] и поэтому здесь не приводятся. Далее с применением функции fp (P) = 0 распределения КМ СКГ между 6 гиродинами вектор потребного управляющего момента СГК Mk = J(уk )mk “пересчитывается” в вектор цифровых команд по скорости прецессии гд ug = рk. При декрементах колебаний 5p = 5a = 0.002 конструкции КА выполнен анализ эффективности дискретных фильтров с периодом квантования Tq = 1 с, Tf = 1.5 с и алгоритмов цифрового управления СГК с периодом дискретности Tu = 4 с, некоторые полученные численные результаты представлены на рис. 4 и рис. 5.

ЗАКЛЮЧЕНИЕ

Кратко рассмотрены актуальные задачи синтеза и анализа цифровой системы cиловой гирос-

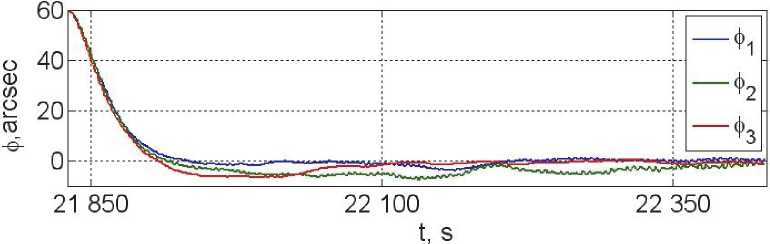
Рис. 4. Переходные процессы по углам ориентации КА относительно ОСК

21 850

22 350

Рис. 5. Переходные процессы по угловым скоростям корпуса КА

копической стабилизации движения крупногабаритного спутника, имеющего упругую слабо демпфированную конструкцию. Представлены разработанные методики полетной идентифика- 3. ции низших резонансных частот конструкции и тензора инерции спутника, построения законов настройки СГК кратной схемы на основе шести гиродинов, а также синтеза алгоритмов дискретной фильтрации доступных измерений и цифро- 4. вого управления СГК.

Работа поддержана РФФИ (проект 11-0801037) и Отделением энергетики, машиностроения, механики и процессов управления РАН (программа фундаментальных исследований № 14).   5 _.