Полевая ионизация кластеров воды, неподвижных на межфазных границах

Рассматривается ионизация кластеров воды неподвижных на межфазных границах раздела в условиях неравновесного потока жидкости, как безызлучательный переход, на основе многоквантовой теории переходов. Такой режим реализуется в пузырьковых средах. Учтен эффект изменения дипольных моментов кластеров при переходе. Получено выражение для вероятности полевой ионизации кластеров воды хемосорбированных на поверхности раздела фаз.

Физические свойства жидкости могут обратимо изменяться в результате ее структурирования на основе механической обработки, особенно , при вращениях ассимметричной жидкости создается механизм обмена между внешними и внутренними степенями свободы молекул, когда возбуждаются низкочастотные моды колебаний. При этом значения относительной статической диэлектрической проницаемости, теплоемкости, вязкости, теплопроводности, диффузии других показателей переноса структурированной среды могут существенно отличаться от справочных равновесных значений (например, для обычной воды). Причиной этих отличий служат протекание химических реакций и физических процессов на молекулярном уровне, связанных с выделением тепла, идущих с отклонением от равновесного больцмановского распределения молекул воды по внутренним степеням свободы. Молекулы воды можно рассматривать как несимметричные волчки. Последнее объяснение представляется наиболее реалистичным и макроскопически наблюдается как кавитационное явление. Развитая кавитация во вращающейся жидкости (в каждом кубическом миллилитре жидкости содержится до 105 кавитационных каверн со средним диаметром около 10 мкм ) создаёт обширные поверхности раздела фаз. Диэлектрическая проницаемость ε воды в тонкой пленке или в капле значительно меньше диэлектрической проницаемости воды в свободном объеме. При уменьшении толщины d плоского слоя воды от 40 до 10 мкм, ее относительная диэлектрическая проницаемость монотонно убывает от номинального равновесного значения ε=81 до значения ε=10±3, т.е. уменьшается почти на порядок. Высокая величина статической диэлектрической проницаемости неструктурированной воды связана с высокими значениями дипольных моментов кластеров (Н2О)n и кластерных ионов.

Рис.1 Кластеры воды на границе фаз в потоке.

Уменьшение диэлектрической проницаемости воды в тонком слоев влечёт понижение ориентационной восприимчивости и частичное "замораживание" в приповерхностных областях результирующих дипольных моментов кластеров.

Толщина поверхностного слоя воды, в котором частично сохраняется дальний порядок молекул, составляет ≈ 0,5dо (20 мкм), а толщина частично упорядоченного поверхностного слоя капли воды ≈0,5Dо (30 мкм). Эффективные толщины поверхностных слоев для плоской поверхности и капли составляют около 11 мкм и 16 мкм,соответственно. При убывании d и D, значение диэлектрической проницаемости воды в пределе стремится к величине ε min , близкой к диэлектрической проницаемости ε л льда в его наиболее распространенной кристаллической модификации I: ε_m i _n≈ ε_л .

В динамических условиях потока возникают переменные электрические поля. При d < dо, D < Dо удельная теплоемкость Св, 152

может приближаться к параметрам твердой фазы, т.к. удельная теплоемкость воды в 2 раза превышает удельную теплоемкость льда [1].

Процессы в кластерах очень сложные и позволяют только формулировать простые физические модели. Например, ионизацию можно сформулировать в рамках многоквантового механизма (многофононного) переноса заряда.

Рассмотрим ионизацию как безизлучательный переход на основе адиабатического аппроксимации, которая позволяет отделить быстрые движения электронов от медленного движения ядер. Адиабатические потенциалы на рис. 2 по координате реакции. Состояние 1 относится к кластеру ассоциату на поверности раздела фаз. Соостояние 2 относится к отталкивательному потенциалу ионизированного кластера. Цель данной работы - показать скорость реакций ионизации на неподвижной границе. Особенностью случая является то , что необходимо взять в рассмотрение роль переменного электромагнитного поля, сгенерированного границей раздела фаз, влияющего на элементарную реакцию процесса, особенно потому что кластеры воды имеют большой дипольный момент 100-1000 Дебай.   Для расчета вероятности перехода разность дипольных моментов основного состояния 1 и конечного электронного состояния 2 важна. Рассмотрим вероятность ионизации кластера переменным полем согласно работе [2] →→ →

A d = d i - d 2 .                                     (1)

Разность возникает из-за перестройки кластера при квантовом переходе 1 ^ 2 . Дипольныйй момент полярных молекул в состояниях i электронных полярных молекул таковы:

→ di = di00 + di11 q, i = 1,2;                             (2)

i - электронная часть дипольного момента полярной молекулы, dq

- дипольный момент q колебания, величина

d

включает в

себя

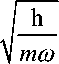
фактор имеющий размерность длины, m - масса осциллятора с частотой to , q - безразмерная координата.

Для простого случая q классических колебаний имеет форму

q = q0 cos(tot + ф).

( 3 )

Формула (3) соответствует классическим движениям ядер

h^< kT, T

постоянная Больцмана).

термодинамическая температура и

k

Энергия

взаимодействия

t

H i

между дипольным моментом

и

электрическим полем d имеет форму — —

Hi = d?0 F + d^ F q0 cos(^t + ф) .(4)

Как следует из формулы (4), второе слагаемое этой формулы имеет вид энергии взаимодействия между постоянным дипольным моментом и переменным электрическим классическим полем

——

F = F cos(tot + ф) .(5)

Поскольку теория многоквантовых переходов под действием переменного электрического поля достаточно развита, то мы можем использовать следствия этой теории для случая классического описания колебаний.

Для вероятности перехода W^ ) с участием квантов электрического поля из 1 состояния в состояние 2 на рис. 2 имеет такой вид:

W2) = W120) J"( Ро),

1   — (1 — (1

Ро =    (d 1 - d 2) Fq о,

h^П = [Г12] + 1 , A12 = ^ — F.

h ^         ^{12     2    1}

Здесь Г 12 - энергетическая щель в электронном переходе 1 — > 2 , J т ⁽ x ) - функция Бесселя реального аргумента , [ A ] - целая часть числа A и J_т ( X ) - энергии i электронных состояний 1 и 2

соответственно.

Когда выводили формулу, мы получили интеграл следующего типа:

∞

i∆

exp{ A1 tt - (n - 1)rot}dt = 2nd( 12 - (n -1)го) h                      h

-∞ где n - целое число, если состояние 2 принадлежит непрерывному спектру ^2 ^ ^1 + [( 2m Л , здесь mg - масса электрона. Затем интегрированием по конечным состояниям, δ- функция удаляется и для П получается условие n = [^ 1 + ^ • Числу П соответствует минимальное число фотонов частотой ω переменного поля , необходимое для ионизации кластера.

Для малых интенсивностей поля F , P g = 1 , тогда получаем Wn ¹ : P 0 " .

Для P 0 — 1 вероятность перехода соответствующему ионизации

W ⁽ n ) 12

резко возрастает как функция ^р о .

Поскольку для кластеров воды интенсивность поля то     P0 — 1 и образом,   ионизация

F : 106 -107 —,     го = 200 см-1, см

(d 1 ) - d2 ))q0 ~ 0.1 - 1D .    Таким неподвижных кластеров на поверхностях раздела фаз водяных пузырей идет со значимой вероятностью и свободных электронов в обьеме достаточно для обеспечения процессов с участием свободных электронов.