Полигауссово описание распределений вероятностей процессов, формируемых нелинейной системой Лоренца, реализованной в числах с фиксированной запятой

Нелинейные системы с динамическим хаосом, обладая уникальной способностью порождать сложные динамические и хаотические процессы, являются объектом активного исследования в современной науке. Эти системы находят широкое применение в различных областях, таких как, например, широкополосные коммуникационные системы, где они служат негармоническими «но- сителями информации», формируя сигналы со сложной шумоподобной колебательной структурой [1]. Это расширяет возможности построения широкополосных систем, минимизируя необходимость модуляции параметров колебаний специализированными двоичными последовательностями [2].

«Прямохаотические» инфокоммуникационные системы базируются на создании сложных негармонических колебаний с высокой частотой в ограниченной полосе частот. Одним из преимуществ этих систем является упрощенность конструкции генератора, состоящего из каскада автогенератора с широкополосной колебательной системой и каскада импульсного модулятора [3; 4]. В существующих публикациях, в основном, описаны относительно упрощенные конструкции приемных устройств [9], такие как детекторные приемники, которые можно адаптировать к частотному диапазону, но не к структурным характеристикам сигнала.

В то же время с целью получения формирователей хаотических сигналов с воспроизводимыми статистическими характеристиками необходимо использование систем, реализованных на основе процедур численного интегрирования. Снижение вычислительных затрат на реализацию подобных систем делает необходимым рассмотрение формирователей хаотических сигналов на основе процедур численного интегрирования с использованием чисел с фиксированной запятой. Эти системы, как подкласс нелинейных систем с динамическим хаосом, предоставляют уникальные возможности для создания прямохаотических коммуникационных систем. Использование чисел с фиксированной запятой способствует снижению вычислительной сложности при цифровой реализации подобных систем [5], что приводит, в конечном счете, к упрощению их практической реализации на современных микросхемах программируемой логики [6].

Вероятностные характеристики играют ключевую роль в описании случайных и псевдослучайных процессов. Описание распределений вероятностей хаотических процессов, формируемых системой Лоренца с помощью полигаус-совых смесей, было проведено в работе [7]. В то же время исследование особенностей подобных описаний для системы Лоренца, реализованной в числах с фиксированной запятой, представляет определенный интерес для техники систем передачи информации. Этот интерес обусловлен как использованием сигналов, формируемых системой Лоренца в качестве прямохаотических носителей информации, так и возможностей использо- вания моделей процессов, формируемых данной системой, для описания комплексной огибающей процессов в реальных каналах связи [10].

Целью данной работы является анализ распределений вероятностей псевдослучайных процессов, сформированных на основе решения системы Лоренца в числах с фиксированной запятой.

Методы и ограничения

Выбранная в качестве объекта исследования система Лоренца может быть записана в виде:

X+i = Xi + A t ( aXi + ^ Y);

“ Y ₊ 1 = Y + A t ( rX i - Y - XZ ) ;       (1)

. Zi+1 = Zi+At(-bZi+ XY), где X, Y, Z – пространственные переменные нелинейных систем с динамическим хаосом; r, а, b - параметры системы Лоренца, At - величина шага численного интегрирования.

В работе проведена аппроксимация плотностей вероятностей сигналов исследуемой системы смесями распределений Гаусса, представленными в виде:

w ( x ) = 2>^г( x , m i , а ) ,          (2)

l = 1

где Г ( x , m i , a i ) - плотности вероятностей распределений Гаусса со средними значениями компонент m_i и среднеквадратическими значениями a i , i = 1, N ; q i - вероятности компонент, причем N

Z q= 1.

i = 1

Сигналы получены на основе использования процедуры Эйлера численного решения систем нелинейных дифференциальных уравнений с применением метода изменения некоторых битов численного представления числа с фиксированной точкой в битовой последовательности:

x = bi + • B + bj + 1 • B +... + b1 • B + bо, (4)

x " = b - I - • B - I - + b - I • B - I ~^{- 1} + ... + b _{- 2} • B - ² + b - 1 • B ^{- 1}, (5)

i+ x = Z bi- Bi,                (6), i=-1 - где младшие биты чисел b-1, b-2, b-3 = random ([0,1]) модифицируются по псевдослучайному закону с целью предотвращения срывов генерации хаотических процессов. Выбранный размер использованных чисел при формировании процессов равен 16.

Анализ результатов

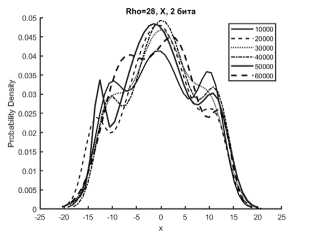
На рисунках 1, 2, 3 представлены аппроксимации гистограмм распределений частот появления

а)

б)

в)

г)

д)

е)

а)

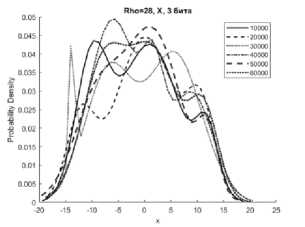
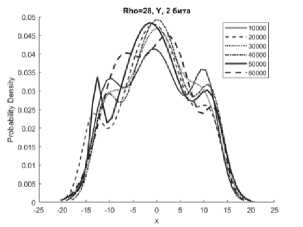
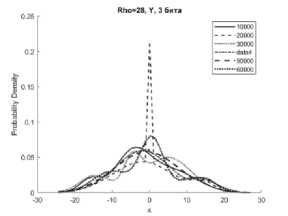
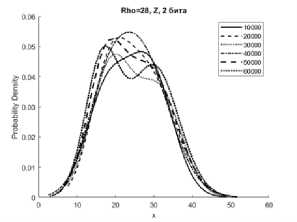
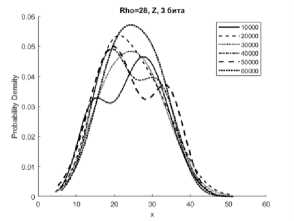
Рисунок 1. Аппроксимации гистограмм распределений частот появления чисел процессов X (сверху), Y (в середине), Z (снизу) системы Лоренца с фиксированной точкой при M=10000…60000 реализаций, r = 28 с изменением 2 и 3 битов информации

б)

в)

г)

д)

е)

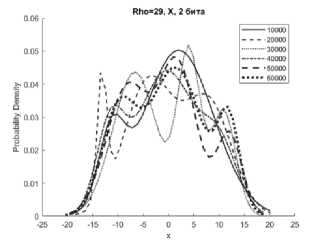
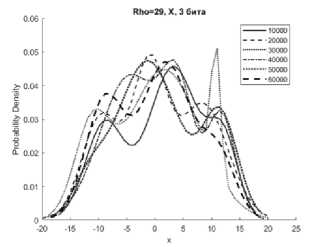
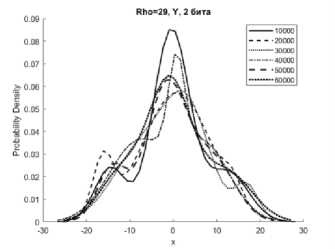
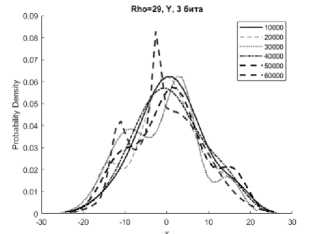
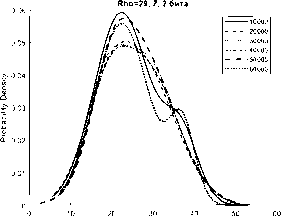
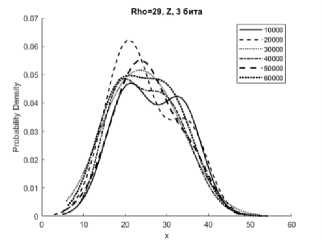
Рисунок 2. Аппроксимации гистограмм распределений частот появления чисел процессов X (сверху), Y (в середине), Z (снизу) системы Лоренца с фиксированной точкой при M=10000…60000 реализаций, r = 29

а)                                     б)                                    в)

г)

д)

е)

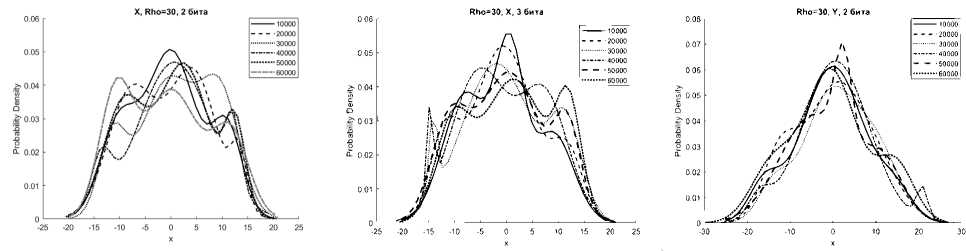
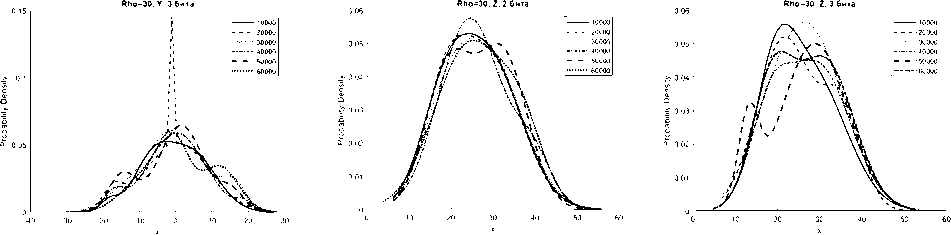
Рисунок 3. Аппроксимации гистограмм распределений частот появления чисел процессов X (сверху), Y (в серединеа), Z (снизу) системы Лоренца с фиксированной точкой при M=10000…60000 реализаций, r = 30

чисел процессов X, Y, Z системы (1) с приведенными модификациями (4), (5), (6) смесью трехкомпонентного полигауссова распределения при различных значениях отношений числа Релея r (Rho на графиках) с различным количеством модифицированных младших битов для формата в числах с фиксированной точкой – 2 и 3 бита.

Представленные аппроксимации приведены для реализаций систем при i=10000, 20000, 30000, 40000, 50000, 60000.

Из графиков видно, что распределение математического ожидания µ и среднеквадратическое отклонение σ для всех реализаций систем при i=10000…60000 имеют полигауссовы распределения вероятностей, что говорит о возможности применения данного метода для формирователей с фиксированной запятой как для систем с псевдослучайными последовательностями.

Особенностью указанных распределений является появление выбросов на определенных временных участках гистограмм рисунков 1б, 1г, 2б, 2г, 3б. Система Лоренца при ее формировании в условиях фиксированной запятой имеет склонность к срыву генерации [8]. Приведенные рисунки показывают, что даже в условиях псевдослучайной модификации 3 младших бит чисел, происходит срыв генерации, сопровождающийся установлением сигнала с фиксированной амплитудой. При применении метода рандомизации младших разрядов это приводит к незначительным изменениям реализаций X, Y за определенные отрезки времени.

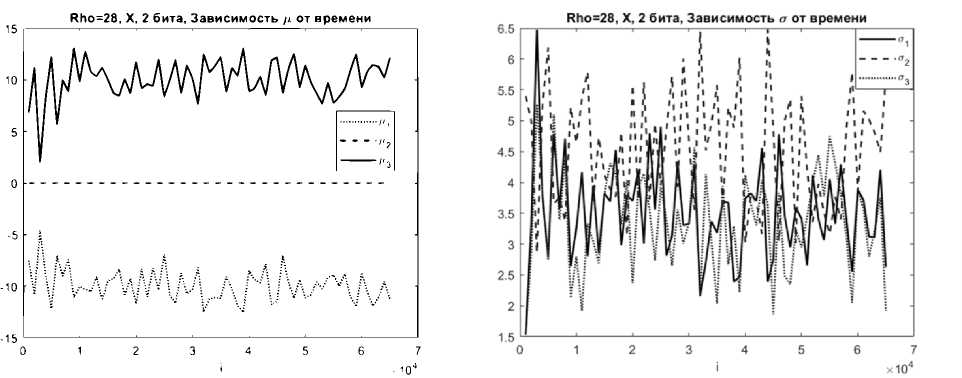
Временные зависимости математических ожиданий и среднеквадратических отклонений аппроксимирующих компонент смеси гауссовых распределений процессов X системы Лоренца приведены на рисунке 4.

На рисунке 4а изображены изменения математических ожиданий µ ₁ , µ ₂ , µ ₃ в зависимости от времени. На графиках видно наличие переходного процесса в системе Лоренца, при котором происходят значительные изменения математических ожиданий в зависимости от времени до точки, соответствующей 10000 отсчетов. При этом также наблюдаются колебания среднеквадратических отклонений компонент с большей амплитудой. На больших интервалах времени размах колебаний математических ожиданий и среднеквадратических отклонений уменьшается, они становятся квазипериодическими. Это говорит о приближении рассматриваемого процесса к стационарному.

Полученные в данной работе результаты по описанию распределений вероятностей псевдослучайных процессов, сформированных на основе решения системы Лоренца в числах с фиксированной запятой в целом достаточно близки к результатам, изложенным в [7] для чисел с плава-

а)

б)

Рисунок 4. Оценки изменений во времени математических ожиданий и среднеквадратических отклонений аппроксимирующих гауссовых компонент процессов X системы Лоренца

ющей запятой. Отличием приведенных результатов является показанные в данной работе срывы генерации псевдослучайных процессов даже при условии рандомизации младших разрядов описывающих их чисел.

Выводы

• 1.    Показана возможность использования поли-гауссова описания распределений вероятностей псевдослучайных процессов, сформированных на основе решения системы Лоренца в числах с фиксированной запятой.

• 2.    Число компонент смеси гауссовых распределений, которые необходимо использовать для описания процессов, формируемых системой Лоренца, составляет не более 3.

• 3.    Применение рандомизации 3 разрядов из 16 в формируемых числах, представляющих процессы, приводит к снижению количества реализаций со срывом генерации.

• 4.    Время установления стационарного режима генерации процессов в системе Лоренца, реализованной над числами с фиксированной запятой, составляет не менее 10000 отсчетов.