Полимерные конструкции композитных материалов

Причиной внедрения наполнителей для изготовления композитных материалов (КМ) конструкционного назначения является получение полимерного материала с комплексом улучшенных физико-механических свойств. Волокнистая, чтобы достичь этогокритик необходимо добавить наполнители, мелкодисперсные наполнители, разрезанные стекловолокна, наноразмерные органические или неорганические частицы и так далее.

Чтобы создать КМ с особыми свойствами, обычно вводятся наполнители, чтобы придать материалу требуемые электрофизические, термические, сенсорные и другие свойства в дополнение к механическим свойствам. В этом случае частицы наполнителя так или иначе распределены в полимерной матрице. По распределению компонентов композиты можно разделить на матричные (регулярные) системы, статистические смеси и структурированные композиты.

На рис. 1. показаны различные структуры композитов и распределение наполнителя в матрице. В матричных системах частица наполнителя находится в узлах регулярной (а) сетки. В статистических системах компоненты распределены хаотично и не образуют регулярной структуры (б). В систему структурированных композитов входят те, компоненты которых образуют цепные, плоские или объемные структуры (v, g).

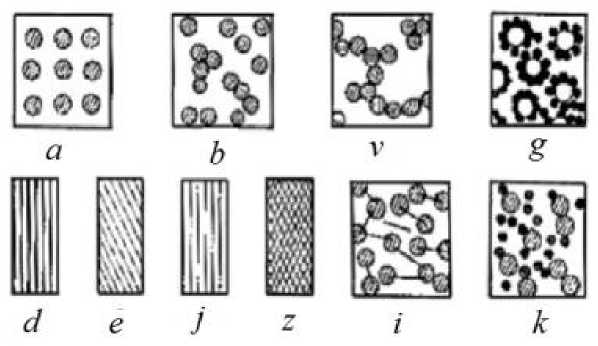
Рисунок 1. Состав состава и распределение наполнителей в матрице.

Топология КМ относится к распределению дисперсной фазы в соответствии с формой частиц дисперсной фазы, их размером и объемом дисперсной среды. Также включены размеры входов, расстояние между ними, центральная координата входов, угол направления в фазе входов неоднородного размера, то есть размеры входов в одном или двух отдельных направлениях. намного больше, чем в другом направлении. Например, для него также характерны волокна, пластины и т. Д.

Сплошные волоконные или тканевые композитные материалы, ориентированные по одной оси, легко подвергаются анализу (рис. 2).

Например, электропроводность КМ в направлении вдоль волокна (в плоскости слоя ткани) (будет рассмотрено в будущем)

eff ,1

c ^— p & f +^{( 1} p j a m (Верхний предел Винера)        (1)

а электропроводность в перпендикулярном направлении

¹ / ^af , — p / ^a f ⁺ ( 1 - p ^m (Нижняя граница Винера)      (2)

определяется как. Это оно на земле ^ f и (Г_т - электропроводность наполнителя и матрицы, p - объемная доля наполнителя. Эти выражения носят общий характер, поскольку фазовые эффекты соответствуют эффективной проводимости двухфазной системы, когда они включены последовательно и параллельно, а оптимизация достигается, когда известна объемная доля каждой фазы.

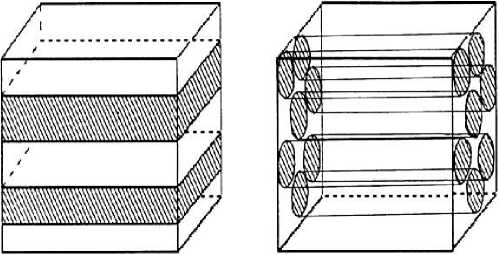
Рисунок 2. Два граничных состояния в микрогеометрическом размещении наполнителя. Электропроводность определяется верхней границей Винера в направлении параллельных слоев. Он определяется нижней границей Винера, перпендикулярной слоям.

Продольная проницаемость для слоистых композиционных материалов С1 всегда больше, чем проницаемость в направлении, перпендикулярном слою. Конечно,ст3 ^i проницаемость и di продольная проницаемость для набора слоев толщиной:

^ =Е di  ^

,

Поперечная проводимость составляет:

1 _Ydi

^"~

Средняя продольная проницаемость:

^

• ¹    = L d i

Средняя поперечная проводимость:

L d

^ eff ,3      ^ 3

Используя неравенство Коши-Буняковского, aeff ,3 < ^eff ,1

выражается.

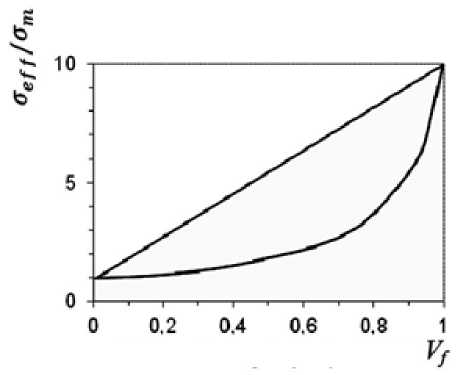
Рис. 3. Эффективная электропроводность композита

^ eff

и концентрация наполнителя для верхнего и нижнего предела Винера

& f

(— = ¹⁰ случай).

^ m

Электропроводность в направлении параллельных слоев определяется по верхней границе Винера. Электропроводность вдоль перпендикулярных слоев определяется между нижним пределом Винера. Верхний и нижний предел Винера определяет значения электропроводности КМ в заданном соотношении параметров матрицы и наполнителя, независимо от формы частиц и метода приготовления КМ (рис.3).