Полиномиально вычислимые -спецификации иерархизированных моделей реагирующих систем

Polynomially computable Σ specifications of hierarchical models of reacting systems

V. N. Glushkova, K. S. Korovina

Don State Technical University (Rostov-on-Don, Russian Federation)

Introduction. Verification packages design and analyze the correctness of parallel and distributed systems within the framework of various classes of temporal logics of linear and branching time. The paper discusses a polynomially realizable class of Δ0T -formulas interpreted on multi-sorted models with hierarchical suspensions. The suspension structure is described by an arbitrary context-free (CF) grammar. The predicates and functions of the model signature are interpreted on the original CF-list, which is completed during the interpretation process.

Materials and Methods. A constant model is constructed for theories from A ₀ T -quasiidentities with Noetherian and confluence properties. We consider formulas of the multi-sorted first-order predicate calculus (PC) language with variables of the “list” sort interpreted on models with a hierarchized suspension. The theory is interpreted in terms of grammar inference trees describing the behavior of the specified system. The CF-grammar rules hierarchize the action space of the modeled system. It is noted that the expressive capabilities of A ₀ T -formulas are insufficient for modeling real-time systems. Therefore, expressions with unbounded universal quantifier V, known as PT formulas, are used for the specification.

Results. The logical specification of an automated complex which consists of a workpiece manipulator is given as an example. The location of the positions is fixed by sensors. The operating cycle of the manipulator is described. The specification of its operation consists in the hierarchization of actions by the rules of the CF-grammar and their description by the first-order PT-formulas taking into account the time values.

Discussion and Conclusions . The paper shows that the class of the considered formulas can be used to model real-time systems. An example of the logical specification of a manipulator behavior control device is given.

Введение . Математически обоснованные практически значимые методы верификации сложных программных и технических систем базируются на аппарате математической логики [1–4]. Известна методика применения этого подхода для различных видов реагирующих систем реального времени (протоколов связи, систем управления, встроенных бортовых систем космической техники и др.). Данная методика позволяет верифицировать системы model cheсking [5–7]. Многочисленные пакеты верификации поддерживают проектирование и анализ корректности параллельных и распределенных систем в рамках различных классов темпоральных логик линейного и ветвящегося времени: LTL, CTL, TCTL и др. [8].

Для моделирования времени в этих системах используется стандартная модель временного автомата. Это конечный автомат, снабженный переменными специального вида — локальными часами. Количественный анализ временных характеристик системы затруднен сложными экспоненциальными алгоритмами построения часовых поясов как классов эквивалентности [9]. Поэтому для упрощения анализа необходимо разработать более выразительный практически значимый языка спецификации.

Предлагается использовать для моделирования язык Σ-спецификаций, выделенный в концепции семантического программирования, которая основана на теоретико-модельном подходе [10]. В этом случае для построения формальной модели анализируемой системы можно использовать язык исчисления предикатов 1-го порядка, расширенный аксиомами для операций над списочными структурами 1,2,3,4 .

Материалы и методы. В работе используется терминология статей [11, 12]. Пусть М — многосортная модель сигнатуры ст = < 7, C , F , R >. Здесь I — множество сортов, включая сорт «cписок» ( list ). C , F , R — множества констант, функций и предикатов соответственно. Все символы сигнатуры имеют тип. Если f= F является n -местной функцией, n >  0, то ее тип равен < i 1 , .. i n , i >, где i 1 , .. i n , i e I , причем i 1 , .. i n — типы аргументов, i — тип значения функции. Аналогично n -местный предикат r e R имеет тип <  i 1 , … i n >. Носитель модели М — индексированное семейство множеств U j = C j , j e I , где C j — множество констант сорта j ; f:

Для модели М над множеством констант С формируется списочная надстройка D G ( С ) из иерархизированных КС-списков, структура которых задается КС-грамматикой G = ( N , T , P ). Здесь N , T — множества нетерминальных и терминальных символов. Множество D G ( C ) определяется как наименьшее множество всех

• 1    Глушкова В. Н. Верификация робототехнических иерархических систем реального времени // Математическое моделирование и биомеханика в современном университете : тез. X Всерос. шк. - семинара. Ростов н/Д ; Таганрог : ЮФУ, 2015. С. 32.

• 2    Глушкова В. Н. Σ - спецификация робототехнических систем реального времени // Алгебра и логика, теория и приложения : тез. междунар. конф. Красноярск : СФУ, 2016. С. 22 – 23.

• 3    Глушкова В. Н. Логические средства диагностики ошибок в иерархических S- моделях // Алгебра и математическая логика : мат - лы междунар. конф. Казань : КФУ, 2011. С. 58 – 59.

• 4    Глушкова В. Н., Коровина К. С. Логическое моделирование роботизированных технологических систем // VIII Всерос. шк. - семинар : тез. Ростов н/Д : ЮФУ, 2013. С. 44.

  Информатика, вычислительная техника и управление

  
  

До-формулы определяются традиционным способом как формулы сигнатуры G с использованием всех логических связок (-, Л, V, ^) и ограниченных кванторов Vx е t,  ^x е t, Vx с t,  ^x с t. Здесь х перемен ная произвольного сорта; t — терм сорта list, не содержащий х; е — отношение принадлежности списку; с — отношение вложенности для списков, определяемое как < а1,...,аn > с < а1,...,аn > , m > n .

Ниже будем использовать лишь ограниченные кванторы вида Ух Е у, Ух Е у, где переменная у сорта list , отношение Е — транзитивное замыкание отношения Е. Обозначим через х индексированную последовательность переменных х ^ , через е — отношение принадлежности или его транзитивное замыкание.

Правила КС-грамматики иерархизируют пространство действий моделируемой системы. Из соображений эффективности вычислений выделяется класс Д _о T -формул с «древесным» префиксом. Введем для элементов списков отношение х — «левее», а именно, для списка < ••• а, р _. > считаем а х р.

Определение. Д _о-формула вида

( V v 1 е r 1 ) . . . ( Vv_m е r_m ) ( n 1 х 1 1 ) ... ( П р x I p ) Ф ( v , r ) , m > 1, p > 0 называется Д _о T -формулой, если и, l j Е (v, г), 1 <  j <  р ; для всех переменных префикса выполняется условие: r ^ ₊₁ = г ,1 или г+1 = v_k, к < t. Если г₊₁ = v_k, то v_i+k Ф v_k и v_i+k Ф r_k для всех к < t.

Легко показать, что префикс Д _о T -формулы в силу ограничений на переменные можно представить в виде дерева с корнем г 1 , вершинами v, г и дугами, идущими из вершины г в вершину v , 1 < t < т .

Выразительных возможностей Д _о T -формул недостаточно для моделирования систем реального времени, циклически функционирующих неограниченно долго. Будем использовать для спецификации ПТ - формулы с неограниченным квантором всеобщности У.

Определение. Формула, полученная из Д _о T- формулы Ф навешиванием неограниченного квантора всеобщности yv Ф(г), называется ПТ - формулой.

Модель М определяется теорией из квазитождеств вида:

• ^(yv i ^Ег 1 )... ^(yy_m ег_т) ⁽ П 1^¹1' )_⁽П _Р^¹ _Р ХфОлг) ^ ф⁽г^,гЭ).

Здесь формула ф ( ф) — это конъюнкция атомных формул (или их отрицаний) вида r , т ₁ = т ₂, (f= т ), f Е F,r Е R, т₁, т ₂ — термы сигнатуры а .

Алгоритм построения модели Int реализует правило вывода modus ponens (если ф и ф^ф , то ф ). Входные данные для интерпретатора — множество начальных значений функций и предикатов вида:

S q = ^{P⁽c⁾,f⁽c⁾ = c „+i |p Е P,f Е F^}, где с — множество констант из n элементов, и > 1.

Аксиомы (ах) обрабатываются в определенном порядке, сначала с позитивными вхождениями предикатов в левую и правую часть ах, потом с негативными вхождениями до получения неподвижных точек вычислений. Область определения функций и предикатов, входящих в правую часть ах, расширяется при истинности ее левой части. Это объясняется тем, что интерпретатор задает новые значения функций и предикатов так, чтобы правая часть ах была тоже истинной. Пусть состояние S_n анализируемой системы на -м шаге вычисления содержит значения всех предикатов и функций сигнатуры модели, а функция т P(S") ^ P(S") в (терминологии [3] — преобразователь предикатов) отражает изменение состояния при переходе интерпретатора Int от n -го шага вычисления к n+ 1. Интерпретатор Int строит для монотонного преобразователя т на P(S") наименьшую неподвижную точку pZ.

t(Z) =U < t¹(S₀) , где t⁰(Z) = Z , Tⁱ⁺¹(Z) = t(t¹(Z)) .

Формально функции f Е F и предикаты p Е R интерпретируются на КС-списке tl(и), представляющем дерево вывода tr(и) в грамматике G, где n — шаг работы Int. Из-за трудности представления компактной формы записи алгоритма интерпретации на элементах КС-списка приведем сначала словесное пояснение алгоритма, ориентируясь на дерево tr(и). Входные данные для алгоритма построения модели (Int): исходное дерево вывода tr(0) в грамматике G, расширяемое в процессе построения модели М и Fact=S0. КС-грамматика используется в процессе построения модели следующим образом. Во -первых, правила P иерархизируют пространство действий и состояний анализируемой системы. Будем считать, что имена действий, представленные в сигнатуре модели предикатами, и имена соответствующих нетерминальных символов грамматики совпадают. Во-вторых, символы из алфавита V грамматики однозначно определяют сорта всех элементов универса модели, включая списки, которым ставится в соответствие сорт, определяемый меткой корня соответствующего дерева. Сорта будем обозначать мнемонично начальными строчными символами имен нетерминальных и терминальных символов грамматики с добавлением в конце символа s (sort). Основное достоинство КС-грамматик состоит в возможности использования эффективных синтаксически ориентированных (СО) методов для анализа корректности (верификации) модели, развитых в теории синтаксического анализа языков программирования.

Интерпретатор начинает работу с просмотра дерева tr(0) от корня сверху вниз, слева направо. Префикс всех аксиом удовлетворяет ограничениям Д₀T-формул. Сорта префикса определяются символами КС-грамматики G . Интерпретатор выбирает в качестве констант области истинности предикатов, входящих в аксиому ах Е Th , константы, сопоставляемые вершинам куста дерева, просматривая его сверху вниз, слева направо. Причем корень куста помечен именем соответствующего предиката. Для отражения зависимости моделируемой технической системы от последовательности входных сигналов необходимо достраивать исходное дерево tr(0). С этой целью последовательность правил рг + (ах) Е Р + приписывается к выводу дерева, полученного на предыдущем шаге работы алгоритма. Причем константы из области истинности предиката г используются в качестве терминальных символов, подчиненных в дереве вершине, помеченной нетерминальным символом г.

Опишем алгоритм интерпретации Int более формально, не детализируя процедуру Con(Q, Th) — получения всех логических следствий из множества формул Q на основе аксиом теории Th. Th0 = S0. Теория Thpos С Th включает только позитивные вхождения предикатов. Thneg С Th включает негативное вхождение предикатов в правой части аксиом. Обозначим trpos, trneg — деревья выводов, генерируемые в процессе интер- претации.

Q :=0;

Q :=Th o ;

while Q Q Q* do

Q pos — Q ;

Q Pos — Q * ;

while ^Qpos ^{Q Q} Pos ^do Qpos ^— Qpos ;

end while return (Qpos , trpos) ;

^Qneg — ⁰;

^Qneg ^{— Q}pos ;

while ^Qneg ^{Q Q}‘eg do

^Qneg ^{— Q}neg ;

end while return (Qneg, trneg);

^Qpos * ^Con(Qpos , ^Thpos^

^Qneg — ^Con(Qneg , ^Thneg‘⁾

Q — Qpos;

Q' — Qneg end while return (Qneg, trneg)

Верификация модели M состоит в проверке свойств, которым должна удовлетворять анализируемая система. Будем выражать эти свойства произвольными Д₀T-формулами. Используя СО-методы проверки формул, можно строить доказательство аналогично [13].

Теорема. Произвольная Д₀T-формула с m -ограниченными кванторами всеобщности проверяется на КС -списке мощности n за время 0(n^m+1).

Мощность списка tl равна мощности множества (s |s Е tl}.

Оценка является верхней, и ее можно понизить до линейной, если проверять формулы с использованием специфичных СО-методов обработки языков.

Результаты исследования. Приведем логическую спецификацию автоматизированного комплекса, состоящего из манипулятора, обслуживающего технологическую линию ( tl ) с двумя позициями: загрузки и разгрузки деталей ( ld и uld соответственно) [14]. Датчики фиксируют положение позиций. Манипулятор функцио-

Информатика, вычислительная техника и управление

нирует циклически, начиная с позиции загрузки.

ЦИКЛ

• 1.    В начальном положении ld для загрузки детали манипулятор поднимает электропривод за 4 сек. Сжимает автоматизированные клещи и берет заготовку (2 сек), опускает электропривод (4 сек) и передвигается вправо к автомату до срабатывания датчика положения tl .

• 2.    Чтобы установить заготовку на автомате на позиции tl , манипулятор поднимает электропривод, разжимает автоматизированные клещи (2 сек), опускает электропривод. Далее манипулятор ожидает 4 мин, после чего повторяет те же процедуры, что и на позиции ld . Затем манипулятор двигается влево к позиции разгрузки до срабатывания концевого выключателя uld .

• 3.    За 8 сек деталь разгружается на конвейер. Манипулятор передвигается влево до фиксации датчика ld на позицию загрузки. Далее процесс работы комплекса циклически повторяется.

Спецификация системы состоит из нескольких уровней. Поведение манипулятора определяется сигналами датчиков, фиксирующих его положение: ld , uld , tl ( — ld , — uld , — tl , отрицание указывает на отсутствие соответствующего сигнала). Эта последовательность сигналов представлена кортежем mc=, y, z...>, где x = ld (—ld) , y = uld (— uld), z=tl (— tl). Она генерируется конечным автоматом с начальным состоянием x. Этот автомат строится по праволинейной грамматике с правилами:

St — ld St 1 1 — ldSt 1 1 e

St 1— — tl St 2 I — i tl St 2

St ₂ — uld St I — uld St.

Обозначим через Dsig множество списков, составленных из цепочек символов, порожденных этой грамматикой.

Внешнее дискретное время (переменная n в логической спецификации) определяется количеством переходов в автомате. Для описания второго уровня функционирования манипулятора используется КС - грамматика, которая указывает последовательность действий ( Oper ) манипулятора:

• —    L , La — загрузка заготовки манипулятором в положении ld и tl соответственно;

• —    Unl , Unla — разгрузка детали в позиции uld и tl ;

• —    Mover , Movel — движение манипулятора направо и налево;

• —    Lstop , Astop , Ulstop — остановка манипулятора в соответствующем положении;

• —    Exp — ожидание;

— Cr — выход из строя управляющего манипулятором устройства.

На состояния манипулятора (символ Pos ) влияют его действия. В указанном примере состояние характеризуется непрерывным временем Timec и дискретным Timed , задаваемым натуральным числом. Значением сорта Timec являются сегменты вида < 1 1 , 1 ₂ > , t₁ , 1 ₂ — константы, причем <  заменяется на ( или [ в зависимости от того, включена левая граница в сегмент времени или нет, аналогично для > .

При спецификации поведения манипулятора абстрагируются от значения времени перемещения манипулятора из одного положения в другое (определяется сигналами с датчиков положения — входными к устройству управления манипулятора). Сигналы, которые подаются на исполнительные механизмы манипулятора для осуществления передвижений и работы автоматизированных клещей, являются выходными.

Ниже представлены правила грамматики G .

• 1.    Start — { Oper } * .

• 2.    Oper — L I La I Unl I Unla I Mover I Movel I Lstop I Astop I Ulstop I Exp I Cr .

• 3.    L — St.

• 4.    La — St .

  
  

• 5.    Unl — State .

• 6.    Unla — State .

• 7.    Mover — State.

• 8 .    Movel — State.

• 9 .    Lstop — State.

• 10.    Astop — State.

• 11.    Ulstop — State.

• 12.    Exp — State.

• 13.    Cr — State .

• 14.    State — Timec Timed I Timed Timed .

• 15.    Timec — Timed I ( Timed , Timed) I [ Timed , Timed) I ( Timed , Timed ] I [ Timed , Timed ].

Timed — класс лексем, значениями которых являются натуральные числа, вычисляемые во время интерпретации теории Th.

В теории Th переменные в формулах обозначаются мнемонично в соответствии с их сортом: р (s tate ) = р ( State ), р ( oper ) = р ( Oper ), р ( n ) = р ( t ) = р ( Timed) , р ( ct ) = р ( Timec ). Предикаты Ld , Tl , Unld определены на множестве Timed . Ld ( n ) истинен, если манипулятор находится на позиции загрузки. Аналогично для Tl ( n ) — на позиции обрабатывающего автомата, Uld ( n ) — на позиции разгрузки. Перечислим области определения остальных предикатов: Lstop , Astop , Ulstop , Mover , Movel , Cr c Timed x Timed ; L , La , Unl , Unla , Exp c Timec x Timed . В формулах используются стандартные функции head (< x_v...x n >) = x , , tail (< x^..x n >) = <  x ₂,... x n > и функция Mc : Timed ^ Dc . Здесь Dc — множество списков из сигналов датчиков.

В начальный момент времени t = 0, n = 1 и на 1-м шаге вычисления выполняется предикат Lstop (0,1);

*

Mc (1) = mc , где mc е Dc . В аксиомах 1-11 переменные t , п и ct связаны ограниченным квантором V s tate е oper , V t , п , ct е state . В аксиомах 12-17 переменная п связана неограниченным квантором V ; s ₀ = <<<<0,1>>>> — начальное значение списка, на котором интерпретируется теория. Составляющие его списки в порядке глубины вложенности имеют сорта р ( R ), р ( Oper ), р ( Lstop ), р (0) = р (1) = р ( Timed ). Списку s ₀ соответствует дерево T ₀ (рис. 1).

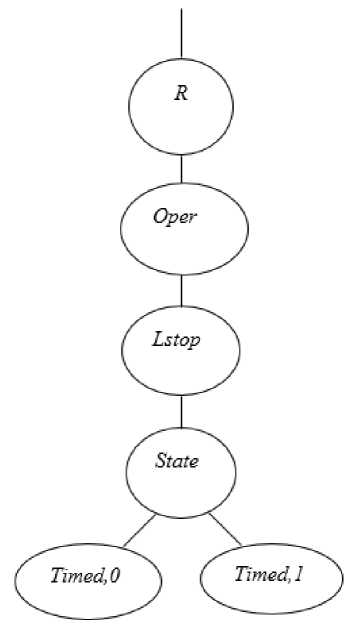
Рис. 1. Дерево T ₀ , соответствующее списку s ₀

В аксиомах теории справа в квадратных скобках приводится последовательность правил грамматики G , достраивающих дерево T 0 .

Аксиомы теории

• 1.    Lstop ( t , n ) л Ld ( n ) ^ L ([ t , t + 7), n ) л Mc ( n + 1) = tail ( Mc ( n )) [1; 2.1; 3; 14.1; 15.3].

• 2.    L ( ct , n ) л Tl ( n + 1) ^ Mover ( ct [2], n + 1) л Astop ( ct [2], n + 1) [1; 2.5; 7; 14.2;1; 2.8; 10; 14.2].

• 3.    Astop ( t , n H Unla ([ t , t + 7], n ) [1; 2.4; 6; 14.1; 15.2].

• 4.    Unla ( ct , n ) ^ Exp (( ct [2], ct [2] + 180), n ) [1; 2.10; 11; 14.1; 15.2]

• 5.    Exp ( ct , n ) ^ La ([ ct [2], ct [2] + 3), n ) л Mc ( n + 1) = tail ( Mc ( n )) [1; 2.2; 4; 14.1; 15.2].

• 6.    La ( ct , n ) л Uld ( n + 1) ^ Movel ( ct [2], n + 1) л Ulstop ( ct [2], n + 1) [1; 2.6; 8; 14.2; 1; 2.9; 11; 14.2].

• 7.    Ulstop ( t , n ) ^ Unl ([ t , t + 7), n ) л Mc ( n + 1) = tail ( Mc ( n )) [1; 2.3; 5; 14.1; 15.2].

• 8.    Unl ( ct , n ) л Ld ( n + 1) ^ Movel ( ct [2], n + 1) л Lstop ( ct [2], n + 1) [1; 2.6; 8; 14.2; 1; 2.7; 9; 14.2].

• 9.    Unl ( ct , n ) л - Ld ( n + 1) ^ Cr ( ct [2], n + 1) [1; 2.11; 13; 14.2].

  Информатика, вычислительная техника и управление

  
  

• 10.    La ( ct , n ) ∧   Unld ( n + 1) → Cr ( ct [2], n + 1) [1; 2.11; 13; 14.2].

• 11.    L ( ct , n ) ∧   Tl ( n+ 1) → Cr ( ct [2], n + 1) [1; 2.11; 13; 14.2].

• 12.    head ( Mc ( n )) = ld → Ld ( n ).

• 13.    head ( Mc ( n )) =   ld →   Ld ( n ).

• 14.    head ( Mc ( n )) = tl → Tl ( n ).

• 15.    head ( Mc ( n )) = tl →   Tl ( n ).

• 16.    head ( Mc ( n )) = uld → Unld ( n )

• 17.    head ( Mc ( n )) = uld →   Uld ( n ).

Теория Th обладает свойством нётеровости, т. к. изменение переменной под квантором ∀ ограничено k — количеством элементов в исходном списке mc. При этом head ( Mc ( k+ 1)) не определено, т. к. Mc ( k+ 1)=< >. Отметим, что цепочки — ld и др. в правой части аксиом 12-17 имеют сорт string , и — рассматривается не как логическая операция, а как символ.

Для начального значения функции Mc (1) = < ld , tl , uld , ld ,   tl , uld > получаем множество следствий: Lstop (0,1), Ld (1), L ([0,7), 1), Mc (2) = <  tl , uld , ld ,   tl , uld >, Mover (7,2), Astop (7,2), Unla ([7, 14], 2), Exp ([14, 194], 2), La ([194, 197), 2), Mc (3) = < uld , ld ,   tl , uld >, Movel (197, 3), Ulstop (197, 3), Unl ([197, 204], 3), Mc (4) = < ld ,   tl , uld >, Movel (204, 4), Lstop (204, 4), L ([204, 211), 4), Mc (5) = <    tl , uld >, Cr (211, 5).

Полученное множество следствий иерархизируется в соответствии с выводом в грамматике G , полученным в результате правил, приписанных к интерпретируемым аксиомам. В соответствии с ними к дереву T 0 справа от узла, помеченного символом Oper , добавляются еще 12 вершин, помеченных этим же символом и связанных ребрами с корнем. К новым вершинам подвешиваются поддеревья с корнями, помеченными символами Ld , Mover , Astop и т. д. с их состояниями и константами сорта ρ ( Timed ), полученными в результате интерпретации.

Обсуждения и заключения . На построенной модели можно проверять истинность произвольных Δ 0 T- формул. Например, формализуем утверждение: «Если манипулятор стоял на позиции загрузки в момент t на шаге п цикла его функционирования, то на шаге п + 2 через 197 сек он начинает разгрузку в течение 7 сек». Приведенная ниже формула проверяется на заданном списке Oper сорта ρ ( Oper ):

( ∀ state ∈ ^* oper ) ( ∀ t ∈ State ) ( ∀ n ∈ state ) ( Lstop ( t , n ) → Unl ([ t + 197, t + 204], n + 2) .